9.4: Variables aleatorias continuas

Función de densidad de probabilidad; función de distribución acumulativa

Dejar\(X\) ser una variable aleatoria que toma cualquier valor real en (digamos) un intervalo,\[X \in[a, b] .\] La función de densidad de probabilidad (pdf) es una función sobre\([a, b], f_{X}(x)\), tal que\[\begin{aligned} f_{X}(x) & \geq 0, \quad \forall x \in[a, b], \\ \int_{a}^{b} f_{X}(x) d x &=1 . \end{aligned}\] Tenga en cuenta que la condición de que la función de masa de probabilidad suma a la unidad es reemplazada por una condición integral para la variable continua. La probabilidad de que\(X\) tome un valor sobre un intervalo infinitesimal de longitud\(d x\) es\[P(x \leq X \leq x+d x)=f_{X}(x) d x,\] o, sobre un subintervalo finito\(\left[a^{\prime}, b^{\prime}\right] \subset[a, b]\),\[P\left(a^{\prime} \leq X \leq b^{\prime}\right)=\int_{a^{\prime}}^{b^{\prime}} f_{X}(x) d x .\] En otras palabras, la probabilidad que\(X\) toma el valor entre \(a^{\prime}\)y\(b^{\prime}\) es la integral de la función de densidad de probabilidad\(f_{X}\) sobre\(\left[a^{\prime}, b^{\prime}\right]\).

Una instancia particular de esto es una función de distribución acumulativa (cdf)\(F_{X}(x)\), que describe la probabilidad de que\(X\) tomará un valor menor que\(x\), es decir,\[F_{X}(x)=\int_{a}^{x} f_{X}(x) d x .\] (También podemos reemplazar\(a\) con\(-\infty\) if definimos\(f_{X}(x)=0\) para\(-\infty<x<a\).) Tenga en cuenta que cualquier cdf satisface las condiciones\[F_{X}(a)=\int_{a}^{a} f_{X}(x) d x=0 \quad \text { and } \quad F_{X}(b)=\int_{a}^{b} f_{X}(x) d x=1\] Además, se deduce fácilmente de la definición\[P\left(a^{\prime} \leq X \leq b^{\prime}\right)=F_{X}\left(b^{\prime}\right)-F_{X}\left(a^{\prime}\right) .\] que Es decir, podemos calcular la probabilidad de\(X\) tomar un valor en\(\left[a^{\prime}, b^{\prime}\right]\) tomando la diferencia del cdf evaluado en los dos puntos finales.

Introduzcamos algunas nociones útiles para caracterizar un pdf, y así el comportamiento de la variable aleatoria. La media,\(\mu\), o el valor esperado,\(E[X]\), de la variable aleatoria\(X\) es\[\mu=E[X]=\int_{a}^{b} f(x) x d x .\] La varianza,\(\operatorname{Var}(X)\), es una medida de la dispersión de los valores que\(X\) toma sobre su media y se define por\[\operatorname{Var}(X)=E\left[(X-\mu)^{2}\right]=\int_{a}^{b}(x-\mu)^{2} f(x) d x .\] La varianza también se puede expresar como\[\begin{aligned} \operatorname{Var}(X) &=E\left[(X-\mu)^{2}\right]=\int_{a}^{b}(x-\mu)^{2} f(x) d x \\ &=\int_{a}^{b} x^{2} f(x) d x-2 \mu \underbrace{\int_{a}^{b} x f(x) d x}_{\mu}+\mu^{2} \int_{a}^{b} f(x) d x \\ &=E\left[X^{2}\right]-\mu^{2} . \end{aligned}\] El cuantil\(\alpha\) -ésimo de una variable aleatoria\(X\) se denota por\(\tilde{z}_{\alpha}\) y satisface\[F_{X}\left(\tilde{z}_{\alpha}\right)=\alpha .\] En otras palabras, el cuantil\(\tilde{z}_{\alpha}\) divide el intervalo\([a, b]\) tal que la probabilidad de\(X\) tomar un valor en\(\left[a, \tilde{z}_{\alpha}\right]\) es\(\alpha\) (y a la inversa\(\left.P\left(\tilde{z}_{\alpha} \leq X \leq b\right)=1-\alpha\right)\). El\(\alpha=1 / 2\) cuantil es la mediana.

Consideremos algunos ejemplos de variables aleatorias continuas.

(a) función de densidad de probabilidad

(b) función de densidad acumulativa

Figura 9.10: Distribuciones uniformes

Ejemplo 9.4.1 Distribución uniforme

Let\(X\) Ser una variable aleatoria uniforme. Entonces,\(X\) se caracteriza por un pdf constante,\[f_{X}(x)=f^{\text {uniform }}(x ; a, b) \equiv \frac{1}{b-a}\] Tenga en cuenta que el pdf satisface la restricción\[\int_{a}^{b} f_{X}(x) d x=\int_{a}^{b} f^{\text {uniform }}(x ; a, b) d x=\int_{a}^{b} \frac{1}{b-a} d x=1\] Además, la probabilidad de que la variable aleatoria tome un valor en el subintervalo\(\left[a^{\prime}, b^{\prime}\right] \in\)\([a, b]\) es\[P\left(a^{\prime} \leq X \leq b^{\prime}\right)=\int_{a^{\prime}}^{b^{\prime}} f_{X}(x) d x=\int_{a^{\prime}}^{b^{\prime}} f^{\text {uniform }}(x ; a, b) d x=\int_{a^{\prime}}^{b^{\prime}} \frac{1}{b-a} d x=\frac{b^{\prime}-a^{\prime}}{b-a}\] En otras palabras, la probabilidad que\(X \in\left[a^{\prime}, b^{\prime}\right]\) es proporcional a la longitud relativa del intervalo ya que la densidad se distribuye por igual. La distribución se denota de forma compacta como\(\mathcal{U}(a, b)\) y escribimos\(X \sim \mathcal{U}(a, b)\). Una integración directa del pdf muestra que la función de distribución acumulativa de\(X \sim \mathcal{U}(a, b)\) es\[F_{X}(x)=F^{\text {uniform }}(x ; a, b) \equiv \frac{x-a}{b-a}\] El pdf y cdf para algunas distribuciones uniformes se muestran en la Figura\(9.10\).

Un ejemplo de los valores tomados por una variable aleatoria uniforme\(\mathcal{U}(0,1)\) se muestra en la Figura\(9.11(\) a). Por construcción, el rango de valores que toma la variable se limita a entre\(a=0\) y\(b=1\). Como era de esperar, no hay una concentración obvia de los valores dentro del rango\([a, b]\). La figura\(9.11(b)\) muestra un histrograma que resume la frecuencia del evento que\(X\) reside en bins\(\left[x_{i}, x_{i}+\delta x\right]\),\(i=1, \ldots, n_{\text {bin. }}\). La frecuencia relativa de ocurrencia se normaliza\(\delta x\) para ser consistente con la definición de la función de densidad de probabilidad. En particular, la integral de la región llenada por el histograma es la unidad. Si bien hay cierta dispersión en las frecuencias de ocurrencias debido a

a) realización

(b) densidad de probabilidad

Figura 9.11: Ilustración de los valores tomados por una variable aleatoria uniforme\((a=0, b=1)\).

el tamaño de muestra relativamente pequeño, el histograma se asemeja a la función de densidad de probabilidad. Esto es consistente con la interpretación frecuencista de la probabilidad.

La media de la distribución uniforme viene dada por\[E[X]=\int_{a}^{b} x f_{X}(x) d x=\int_{a}^{b} x \frac{1}{b-a} d x=\frac{1}{2}(a+b)\] Esto concuerda con nuestra intuición, porque si\(X\) es tomar un valor entre\(a\) y\(b\) con igual probabilidad, entonces la media sería el punto medio del intervalo. La varianza de la distribución uniforme es\[\begin{aligned} \operatorname{Var}(X) &=E\left[X^{2}\right]-(E[X])^{2}=\int_{a}^{b} x^{2} f_{X}(x) d x-\left(\frac{1}{2}(a+b)\right)^{2} \\ &=\int_{a}^{b} \frac{x^{2}}{b-a} d x-\left(\frac{1}{2}(a+b)\right)^{2}=\frac{1}{12}(b-a)^{2} \end{aligned}\]

Ejemplo 9.4.2 Distribución normal

Dejar\(X\) ser una variable aleatoria normal. Entonces la función de densidad de probabilidad de\(X\) es de la forma\[f_{X}(x)=f^{\text {normal }}\left(x ; \mu, \sigma^{2}\right) \equiv \frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right)\] El pdf se parametriza por dos variables, la media\(\mu\) y la varianza\(\sigma^{2}\). (Más precisamente escribiríamos así\(X_{\left.\mu, \sigma^{2} .\right)}\) Note que la densidad es distinta de cero sobre todo el eje real y así en principio\(X\) puede tomar cualquier valor. La distribución normal se denota de manera concisa por\(X \sim \mathcal{N}\left(\mu, \sigma^{2}\right)\). La función de distribución acumulativa de una distribución normal toma la forma\[F_{X}(x)=F^{\text {normal }}\left(x ; \mu, \sigma^{2}\right) \equiv \frac{1}{2}\left[1+\operatorname{erf}\left(\frac{x-\mu}{\sqrt{2} \sigma}\right)\right]\]

(a) función de densidad de probabilidad

(b) función de densidad acumulativa

Figura 9.12: Distribuciones normales

donde erf es la función de error, dada por\[\operatorname{erf}(x)=\frac{2}{\pi} \int_{0}^{x} e^{-z^{2}} d z\] Observamos que es costumbre denotar el cdf para la distribución normal estándar (i.e.\(\mu=0\),\(\sigma^{2}=1\)) por\(\Phi\), es decir\[\Phi(x)=F^{\text {normal }}\left(x ; \mu=0, \sigma^{2}=1\right)\] Veremos muchos usos de este cdf en las secciones posteriores. El pdf y cdf para algunas distribuciones normales se muestran en la Figura\(9.12\).

Un ejemplo de los valores tomados por una variable aleatoria normal se muestra en la Figura\(9.13\). Como ya se señaló, en principio\(X\) puede tomar cualquier valor real; sin embargo, en la práctica, como la función gaussiana decae rápidamente lejos de la media, la probabilidad de\(X\) tomar un valor a muchas desviaciones estándar lejos de la media es pequeña. La figura ilustra\(9.13\) claramente que los valores tomados por\(X\) se agrupan cerca de la media. En particular, podemos deducir del cdf que\(X\) toma valores dentro\(\sigma, 2 \sigma\), y\(3 \sigma\) de la media con probabilidad\(68.2 \%, 95.4 \%\), y\(99.7 \%\), respectivamente. En otras palabras, la probabilidad de\(X\) tomar del valor fuera de la\(\mu \pm 3 \sigma\) viene dada por\[1-\int_{\mu-3 \sigma}^{\mu+3 \sigma} f^{\text {normal }}\left(x ; \mu, \sigma^{2}\right) d x \equiv 1-\left(F^{\text {normal }}\left(\mu+3 \sigma ; \mu, \sigma^{2}\right)-F^{\text {normal }}\left(\mu-3 \sigma ; \mu, \sigma^{2}\right)\right) \approx 0.003\] Podemos calcular fácilmente algunos cuantiles en base a esta información. Por ejemplo,\[\tilde{z}_{0.841} \approx \mu+\sigma, \quad \tilde{z}_{0.977} \approx \mu+2 \sigma, \quad \text { and } \quad \tilde{z}_{0.9987} \approx \mu+3 \sigma\] Vale la pena mencionar que\(\tilde{z}_{0.975} \approx \mu+1.96 \sigma\), ya que frecuentemente utilizaremos esta constante en las secciones posteriores.

Aunque solo consideramos variables aleatorias discretas o continuas en estas notas, las variables aleatorias pueden mezclarse discretas y continuas en general. Las variables aleatorias mixtas discretas-continuas se caracterizan por la aparición de discontinuidades en su función de distribución acumulativa.

a) realización

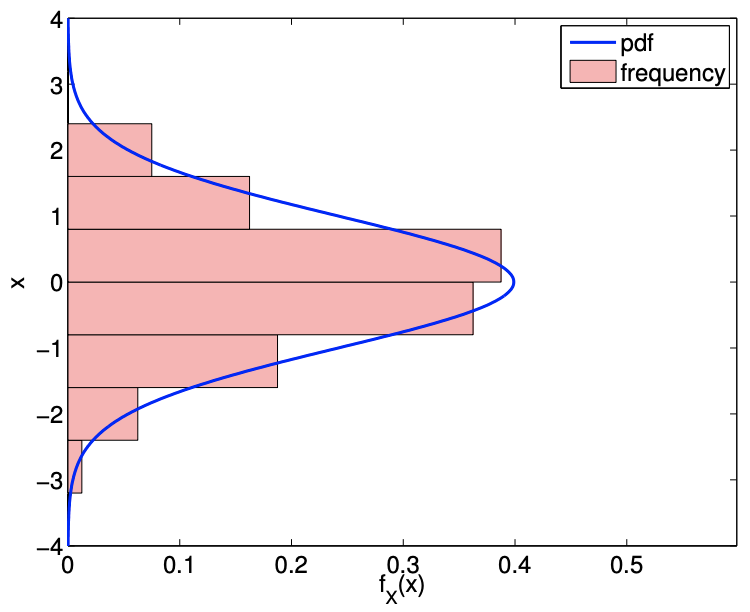
(b) densidad de probabilidad

Figura 9.13: Ilustración de los valores tomados por una variable aleatoria normal\((\mu=0, \sigma=1)\).

Transformaciones de variables aleatorias continuas

Al igual que las variables aleatorias discretas, las variables aleatorias continuas pueden ser transformadas por una función. La transformación de una variable aleatoria\(X\) por una función\(g\) produce otra variable aleatoria,\(Y\), y denotamos esto por\[Y=g(X)\] Consideraremos aquí solo funciones monótonas\(g\).

Recordemos que hemos descrito la variable aleatoria\(X\) por distribución\[P(x \leq X \leq x+d x)=f_{X}(x) d x\] La variable transformada sigue\[P(y \leq Y \leq y+d y)=f_{Y}(y) d y\] Sustitución de\(y=g(x)\) y\(d y=g^{\prime}(x) d x\) y anotando\(g(x)+g^{\prime}(x) d x=g(x+d x)\) resultados en\[\begin{aligned} f_{Y}(y) d y &=P\left(g(x) \leq g(X) \leq g(x)+g^{\prime}(x) d x\right)=P(g(x) \leq g(X) \leq g(x+d x)) \\ &=P(x \leq X \leq x+d x)=f_{X}(x) d x \end{aligned}\] En otras palabras, \(f_{Y}(y) d y=f_{X}(x) d x\). Este es el análogo continuo a\(f_{Y}\left(y_{j}\right)=p_{j}=f_{X}\left(x_{j}\right)\) en el caso discreto.

Podemos manipular la expresión para obtener una expresión explícita para\(f_{Y}\) en términos de\(f_{X}\) y\(g\). Primero observamos (a partir de la monotonicidad) que\[y=g(x) \quad \Rightarrow \quad x=g^{-1}(y) \quad \text { and } \quad d x=\frac{d g^{-1}}{d y} d y\] Sustitución de las expresiones en\(f_{Y}(y) d y=f_{X}(x) d x\) rendimientos\[f_{Y}(y) d y=f_{X}(x) d x=f_{X}\left(g^{-1}(y)\right) \cdot \frac{d g^{-1}}{d y} d y\] o,\[f_{Y}(y)=f_{X}\left(g^{-1}(y)\right) \cdot \frac{d g^{-1}}{d y} .\] Por el contrario, también podemos obtener una expresión explícita para\(f_{X}\) en términos de\(f_{Y}\) y\(g\). De\(y=g(x)\) y\(d y=g^{\prime}(x) d x\), obtenemos\[f_{X}(x) d x=f_{Y}(y) d y=f_{Y}(g(x)) \cdot g^{\prime}(x) d x \quad \Rightarrow \quad f_{X}(x)=f_{Y}(g(x)) \cdot g^{\prime}(x) .\] Consideraremos varias solicitudes a continuación.

Suponiendo que\(X\) adquiere un valor entre\(a\) y\(b\), y\(Y\) toma un valor entre\(c\) y\(d\), la media de\(Y\) es de\[E[Y]=\int_{c}^{d} y f_{Y}(y) d y=\int_{a}^{b} g(x) f_{X}(x) d x,\] donde se deriva la segunda igualdad \(f_{Y}(y) d y=f_{X}(x) d x\)y\(y=g(x)\).

Ejemplo 9.4.3 Distribución uniforme estándar a una distribución uniforme general

Como primer ejemplo, consideremos la distribución uniforme estándar\(U \sim \mathcal{U}(0,1)\). Deseamos generar una distribución uniforme general\(X \sim \mathcal{U}(a, b)\) definida en el intervalo\([a, b]\). Debido a que una distribución uniforme está determinada únicamente por los dos puntos finales, simplemente necesitamos mapear el punto final 0 a\(a\) y el punto 1 a\(b\). Esto se logra mediante la transformación.\[g(u)=a+(b-a) u .\] Así,\(X \sim \mathcal{U}(a, b)\) se obtiene mapeando\(U \sim \mathcal{U}(0,1)\) como\[X=a+(b-a) U .\]

Prueba

La prueba sigue directamente de la transformación de la función de densidad de probabilidad. La función de densidad de probabilidad de\(U\) es\[f_{U}(u)=\left\{\begin{array}{ll} 1, & u \in[0,1] \\ 0, & \text { otherwise } \end{array} .\right.\] La inversa de la transformación\(x=g(u)=a+(b-a) u\) es\[g^{-1}(x)=\frac{x-a}{b-a} .\] A partir de la transformación de la función de densidad de probabilidad,\(f_{X}\) es\[f_{X}(x)=f_{U}\left(g^{-1}(x)\right) \cdot \frac{d g^{-1}}{d x}=f_{U}\left(\frac{x-a}{b-a}\right) \cdot \frac{1}{b-a} .\] Observamos que\(f_{U}\) evalúa a 1 si \[0 \leq \frac{x-a}{b-a} \leq 1 \quad \Rightarrow \quad a \leq x \leq b,\]y\(f_{U}\) evalúa a 0 de lo contrario. Por lo tanto,\(f_{X}\) simplifica a\[f_{X}(x)=\left\{\begin{array}{l} \frac{1}{b-a}, \quad x \in[a, b] \\ 0, \quad \text { otherwise } \end{array}\right.\] lo que es precisamente la función de densidad de probabilidad de\(\mathcal{U}(a, b)\).

Ejemplo 9.4.4 Distribución uniforme estándar a una distribución discreta

La distribución uniforme también se puede mapear a una variable aleatoria discreta. Considerar una variable aleatoria discreta\(Y\) toma tres valores\((J=3)\),\[y_{1}=0, \quad y_{2}=2, \quad \text { and } \quad y_{3}=3\] con probabilidad\[f_{Y}(y)= \begin{cases}1 / 2, & y_{1}=0 \\ 1 / 4, & y_{2}=2 \\ 1 / 4, & y_{3}=3\end{cases}\] Para generar\(Y\), podemos considerar una función discontinua\(g\). Para obtener la distribución de probabilidad discreta deseada, subdividimos el intervalo\([0,1]\) en tres subintervalos de longitudes apropiadas. En particular, para generar\(Y\), consideramos\[g(x)=\left\{\begin{array}{ll} 0, & x \in[0,1 / 2) \\ 2, & x \in[1 / 2,3 / 4) \\ 3, & x \in[3 / 4,1] \end{array} .\right.\] Si consideramos\(Y=g(U)\), tenemos\[Y= \begin{cases}0, & U \in[0,1 / 2) \\ 2, & U \in[1 / 2,3 / 4) \\ 3, & U \in[3 / 4,1]\end{cases}\] Porque la probabilidad de que la variable aleatoria uniforme estándar tome un valor dentro de un subintervalo\(\left[a^{\prime}, b^{\prime}\right]\) es igual a\[P\left(a^{\prime} \leq U \leq b^{\prime}\right)=\frac{b^{\prime}-a^{\prime}}{1-0}=b^{\prime}-a^{\prime},\] la probabilidad que\(Y\) toma en 0 es\(1 / 2-0=1 / 2\), en 2 es\(3 / 4-1 / 2=1 / 4\), y en 3 es\(1-3 / 4=1 / 4\). Esto da la distribución de probabilidad deseada de\(Y\).

Ejemplo 9.4.5 Distribución normal estándar a una distribución normal general

Supongamos que tenemos la distribución normal estándar\(Z \sim \mathcal{N}(0,1)\) y deseamos mapearla a una distribución normal general\(X \sim \mathcal{N}\left(\mu, \sigma^{2}\right)\) con la media\(\mu\) y la varianza\(\sigma^{2}\). La transformación viene dada por\[X=\mu+\sigma Z .\] Inversamente, podemos mapear cualquier distribución normal a la distribución normal estándar por\[Z=\frac{X-\mu}{\sigma}\]

Prueba

La función de densidad de probabilidad de la distribución normal estándar\(Z \sim \mathcal{N}(0,1)\) es\[f_{Z}(z)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{z^{2}}{2}\right) .\] Usando la transformación de la densidad de probabilidad y el mapeo inverso,\(z(x)=(x-\mu) / \sigma\), obtenemos\[f_{X}(x)=f_{Z}(z(x)) \frac{d z}{d x}=f_{Z}\left(\frac{x-\mu}{\sigma}\right) \cdot \frac{1}{\sigma} .\] Sustitución de la función de densidad de probabilidad\(f_{Z}\) rendimientos \[f_{X}(x)=\frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}\right) \cdot \frac{1}{\sigma}=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right),\]que es exactamente la función de densidad de probabilidad de\(\mathcal{N}\left(\mu, \sigma^{2}\right)\).

Ejemplo 9.4.6 Transformación general por cdf inversa,\(F^{-1}\)

En general, si\(U \sim \mathcal{U}(0,1)\) y\(F_{Z}\) es la función de distribución acumulativa de la que deseamos dibujar una variable aleatoria\(Z\), entonces\[Z=F_{Z}^{-1}(U)\] tiene la función de distribución acumulativa deseada,\(F_{Z}\).

Prueba

La prueba es directa a partir de la definición de la función de distribución acumulativa, es decir,\[P(Z \leq z)=P\left(F_{Z}^{-1}(U) \leq z\right)=P\left(U \leq F_{Z}(z)\right)=F_{Z}(z) .\] Aquí requerimos que\(F_{Z}\) sea monótonamente creciente para ser invertible.

Teorema de Límite Central

La ubicuidad de la distribución normal deriva del teorema del límite central. (La densidad normal también es muy conveniente, con\(\left(\sigma^{2}\right)\) parámetros intuitivos de ubicación\((\mu)\) y escala). El teorema de límites centrales establece que la suma de un número suficientemente mayor de variables aleatorias i.i.d. tiende a una distribución normal. Es decir, si un experimento se repite un mayor número de veces, el resultado en promedio se acerca a una distribución normal. Específicamente, dadas i.i.d. variables aleatorias\(X_{i}, i=1, \ldots, N\), cada una con la media\(E\left[X_{i}\right]=\mu\) y varianza\(\operatorname{Var}\left[X_{i}\right]=\sigma^{2}\), su suma converge a\[\sum_{i=1}^{N} X_{i} \rightarrow \mathcal{N}\left(\mu N, \sigma^{2} N\right), \quad \text { as } \quad N \rightarrow \infty\]

a) Suma de variables aleatorias uniformes

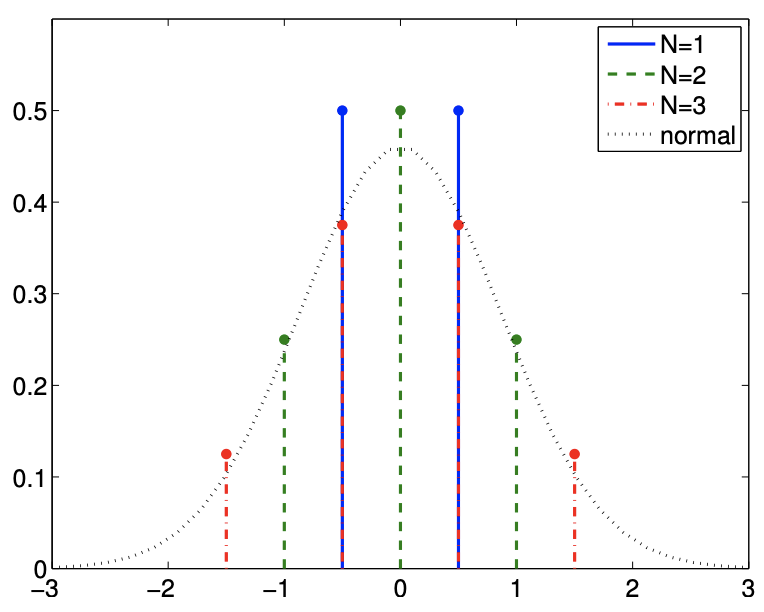
b) Suma de variables aleatorias de Bernoulli (desplazadas)

Figura 9.14: Ilustración del teorema del límite central para variables aleatorias continuas y discretas.

(Hay una serie de hipótesis matemáticas que deben ser satisfechas.)

Para ilustrar el teorema, consideremos la suma de variables aleatorias uniformes\(X_{i} \sim \mathcal{U}(-1 / 2,1 / 2)\). La media y varianza de la variable aleatoria son\(E\left[X_{i}\right]=0\) y\(\operatorname{Var}\left[X_{i}\right]=1 / 3\), respectivamente. Por teorema de límite central, esperamos su suma\(Z_{N}\),, acercarse\[Z_{N} \equiv \sum_{i=1}^{N} X_{i} \rightarrow \mathcal{N}\left(\mu N, \sigma^{2} N\right)=\mathcal{N}(0, N / 3) \quad \text { as } \quad N \rightarrow \infty\] El pdf de la suma\(Z_{i}, i=1,2,3\), y la distribución normal se\(\left.\mathcal{N}(0, N / 3)\right|_{N=3}=\mathcal{N}(0,1)\) muestran en la Figura\(9.14(\mathrm{a})\). A pesar de que la distribución uniforme original\((N=1)\) está lejos de ser normal y no\(N=3\) es un número grande, el pdf para\(N=3\) puede aproximarse estrechamente por la distribución normal, confirmando el teorema del límite central en este caso particular.

El teorema también se aplica a la variable aleatoria discreta. Por ejemplo, consideremos la suma de (desplazada) Bernoulli variables aleatorias,\[X_{i}=\left\{\begin{aligned} -1 / 2, & \text { with probability } 1 / 2 \\ 1 / 2, & \text { with probability } 1 / 2 \end{aligned}\right.\] Tenga en cuenta que el valor que\(X\) toma se desplaza\(-1 / 2\) en comparación con la variable aleatoria estándar de Bernoulli, de tal manera que la variable tiene media cero. La varianza de la distribución es\(\operatorname{Var}\left[X_{i}\right]=1 / 4\). Como se trata de una distribución discreta, su suma también toma valores discretos; sin embargo, la Figura\(9.14(\mathrm{~b})\) muestra que la función de masa de probabilidad puede aproximarse estrechamente por el pdf para la distribución normal.

Generación de números pseudoaleatorios

Para generar una realización de una variable aleatoria\(X\) -también conocida como variable aleatoria- computacionalmente, podemos usar un generador de números pseudo-aleatorios. Los generadores de números pseudo-aleatorios son algoritmos que generan una secuencia de números que parecen ser aleatorios. Sin embargo, la secuencia real generada está completamente determinada por una semilla, la variable que especifica el estado inicial del generador. Es decir, dada una semilla, la secuencia de los números generados es completamente determinista y reproducible. Así, para generar una secuencia diferente cada vez, se siembra un generador de números pseudo-aleatorios con una cantidad que no es fija; una opción común es usar el tiempo de máquina actual. Sin embargo, la naturaleza determinista del número pseudoaleatorio puede ser útil, por ejemplo, para depurar un código.

Un lenguaje de computadora típico viene con una biblioteca que produce la distribución uniforme continua estándar y la distribución normal estándar. Para generar otras distribuciones, podemos aplicar las transformaciones que consideramos anteriormente. Por ejemplo, supongamos que tenemos un generador de números pseudoaleatorios que genera la realización de\(U \sim \mathcal{U}(0,1)\),\[u_{1}, u_{2}, \ldots .\] Entonces, podemos generar una realización de una distribución uniforme general\(X \sim \mathcal{U}(a, b)\),\[x_{1}, x_{2}, \ldots\] mediante el uso de la transformación\[x_{i}=a+(b-a) u_{i}, \quad i=1,2, \ldots .\] De igual manera, podemos generar dada una realización de la distribución normal estándar\(Z \sim \mathcal{N}(0,1)\),\(z_{1}, z_{2}, \ldots\), podemos generar una realización de una distribución normal general\(X \sim \mathcal{N}\left(\mu, \sigma^{2}\right), x_{1}, x_{2}, \ldots\), por\[x_{i}=\mu+\sigma z_{i}, \quad i=1,2, \ldots .\] Estas dos transformaciones son quizás las más comunes.

Finalmente, si deseamos generar un número aleatorio discreto\(Y\) con la función de masa de probabilidad\[f_{Y}(y)=\left\{\begin{array}{ll} 1 / 2, & y_{1}=0 \\ 1 / 4, & y_{2}=2 \\ 1 / 4, & y_{3}=3 \end{array},\right.\] podemos mapear una realización de la distribución uniforme continua estándar\(U \sim \mathcal{U}(0,1), u_{1}, u_{2}, \ldots\), de acuerdo con\[y_{i}=\left\{\begin{array}{ll} 0, & u_{i} \in[0,1 / 2) \\ 2, & u_{i} \in[1 / 2,3 / 4) \\ 3, & u_{i} \in[3 / 4,1] \end{array} \quad i=1,2, \ldots\right.\] (Muchos lenguajes de programación soportan directamente el pmf uniforme.)

De manera más general, utilizando el procedimiento descrito en el Ejemplo 9.4.6, podemos muestrear una variable aleatoria\(Z\) con función de distribución acumulativa\(F_{Z}\) mapeando realizaciones de la distribución uniforme estándar,\(u_{1}, u_{2}, \ldots\) según\[z_{i}=F_{Z}^{-1}\left(u_{i}\right), \quad i=1,2, \ldots .\] Observamos que hay son otras técnicas de muestreo que son aún más generales (si no siempre eficientes), como los enfoques de “aceptación-rechazo”.