12.2: Cálculo de Volúmenes en Dimensiones Superiores

Tres dimensiones

Tanto el método de Montecarlo como la suma de Riemann utilizados para estimar el área de región\(D\) en dos dimensiones se extiende trivialmente a dimensiones superiores. Consideremos sus aplicaciones en tres dimensiones.

Montecarlo

Ahora, tomamos muestras de\(\left(X_{1}, X_{2}, X_{3}\right)\) manera uniforme a partir de un paralelepípedo\(R=\left[a_{1}, b_{1}\right] \times\left[a_{2}, b_{2}\right] \times\left[a_{3}, b_{3}\right]\), donde los\(X_{i}\)'s son mutuamente independientes. Luego, asignamos una variable aleatoria de Bernoulli según si\(\left(X_{1}, X_{2}, X_{3}\right)\) está dentro o fuera\(D\) como antes, es decir,\[B= \begin{cases}1, & \left(X_{1}, X_{2}, X_{3}\right) \in D \\ 0, & \text { otherwise }\end{cases}\] Recordemos que la convergencia de la media de la muestra con el valor verdadero -en particular la convergencia del intervalo de confianza- está relacionada con la Bernoulli variable aleatoria y no la\(X_{i}\)'s Así, incluso en tres dimensiones, todavía esperamos que el error converja como\(N^{-1 / 2}\), donde\(N\) está el tamaño de la muestra.

Suma de Riemann

Por simplicidad, supongamos que el paralelepípedo es un cubo, es decir,\(a=a_{1}=a_{2}=a_{3}\) y\(b=b_{1}=b_{2}=b_{3}\). Consideramos una cuadrícula de\(N\) puntos centrada en pequeños cubos de tamaño\[h^{3}=\frac{b-a}{N},\] tal que\(N h^{3}=V_{R}\). Ampliando el caso bidimensional, estimamos el volumen de la región\(D\) según\[\frac{\widehat{V}_{D}^{\mathrm{Rie}}}{V_{R}}=\frac{\text { number of points in } D}{N} .\] Sin embargo, a diferencia del método de Monte Carlo, el cálculo del error depende de la dimensión. El error viene dado por\[\begin{aligned} \text { error } & \approx(\text { number of cubes that intersect } D) \cdot h^{3} \\ & \approx\left(\text { surface area of } D / h^{2}\right) \cdot h^{3} \\ & \approx h \approx N^{-1 / 3} . \end{aligned}\] Note que la tasa de convergencia ha disminuido de\(N^{-1 / 2}\) a al\(N^{-1 / 3}\) pasar de dos a tres dimensiones.

Ejemplo 12.2.1 Integración de una esfera

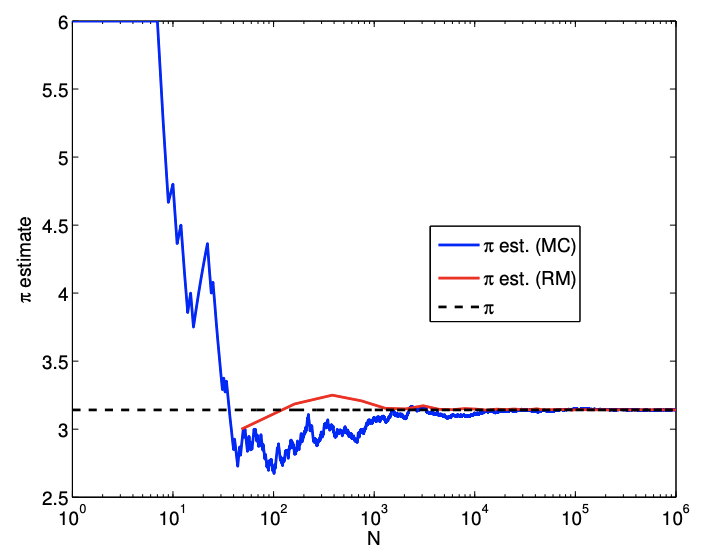
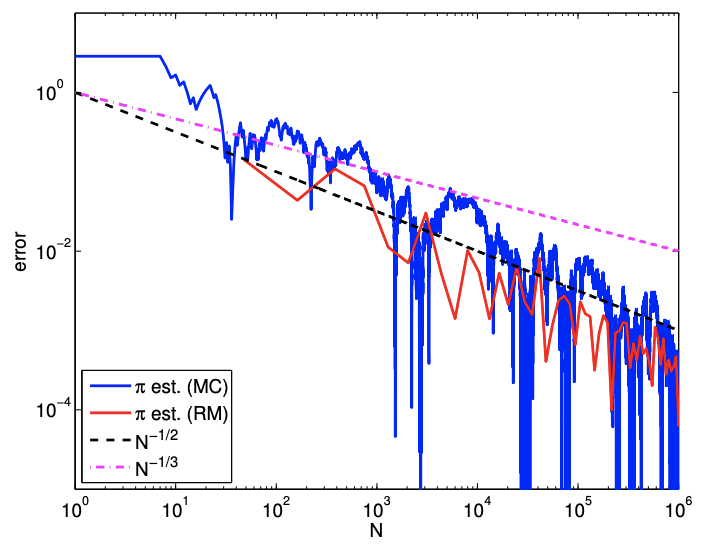
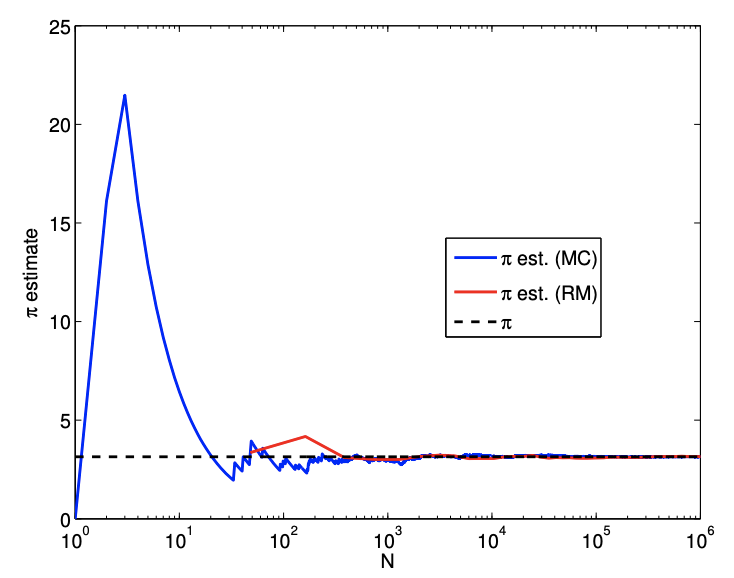
Consideremos el problema de encontrar el volumen de una unidad\(1 / 8\) de esfera situada en el primer octante. Tomamos muestras de un cubo unitario\[R=[0,1] \times[0,1] \times[0,1]\] que tiene un volumen de\(V_{R}=1.0\). Como en el caso del círculo en dos dimensiones, podemos realizar una simple verificación de entrada/salida midiendo la distancia del punto desde el origen; es decir, la variable Bernoulli se asigna de acuerdo a\[b_{n}=\left\{\begin{array}{ll} 1, & \sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}} \leq 1 \\ 0, & \text { otherwise } \end{array} .\right.\] El resultado de estimar el valor de con\(\pi\) base en la estimación del volumen del \(1 / 8\)La esfera se muestra en la Figura 12.7. (El volumen bruto estimado de la esfera 1/8 se escala en 6.) Como se esperaba

(a) valor

(b) error

Figura 12.7: Convergencia de la\(\pi\) estimación utilizando el volumen de una esfera.

tanto el método Montecarlo como la suma de Riemann convergen al valor correcto. En particular, el método Montecarlo converge a la tasa esperada de\(N^{-1 / 2}\). La suma de Riemann, en cambio, converge a un ritmo más rápido que el ritmo esperado de\(N^{-1 / 3}\). Esta superconvergencia se debe a la simetría en la tetraedralización utilizada en la integración y el volumen de interés. Esto no contradice nuestro análisis a priori, porque el análisis nos dice la tasa de convergencia asintótica para el peor de los casos. El siguiente ejemplo muestra que la tasa de convergencia asintótica de la suma de Riemann para una geometría general es efectivamente\(N^{-1 / 2}\).

Ejemplo 12.2.2 Integración de un paralelepípedo

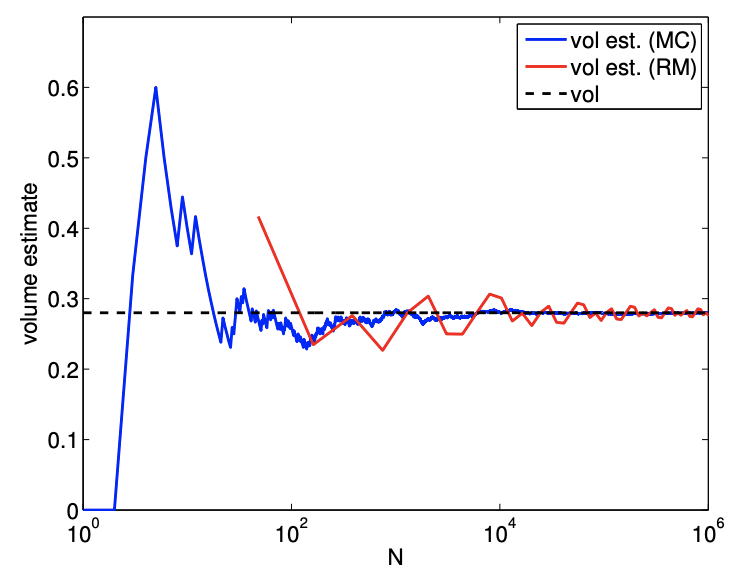
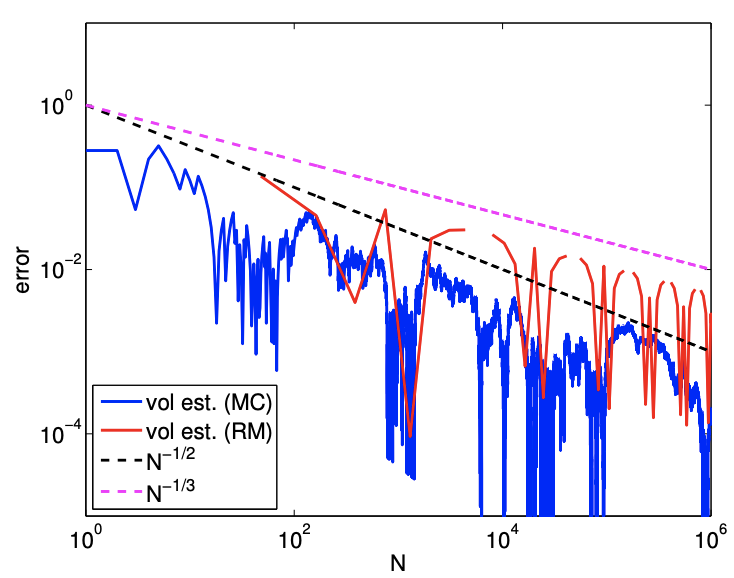
Consideremos un ejemplo más sencillo de encontrar el volumen de un paralelepípedo descrito por\[D=[0.1,0.9] \times[0.2,0.7] \times[0.1,0.8] .\] El volumen del paralelepípedo es\(V_{D}=0.28\).

La figura\(12.8\) muestra el resultado de la integración. La figura muestra que la tasa de convergencia de la suma de Riemann es\(N^{-1 / 3}\), lo cual es consistente con el análisis a priori. Por otro lado, el método Montecarlo funciona igual de bien como lo hizo en dos dimensiones, convergiendo a la velocidad de\(N^{-1 / 2}\). En particular, el método Monte Carlo se desempeña notablemente mejor que la suma de Riemann para grandes valores de\(N\).

Ejemplo 12.2.3 Integración de un volumen complejo

Consideremos una geometría más general, con el dominio definido en la coordenada esférica como\[D=\left\{(r, \theta, \phi): r \leq \sin (\theta)\left(\frac{2}{3}+\frac{1}{3} \cos (40 \phi)\right), 0 \leq \theta \leq \frac{\pi}{2}, 0 \leq \phi \leq \frac{\pi}{2}\right\} .\] El volumen de la región viene dado por\[V_{D}=\int_{\phi=0}^{\pi / 2} \int_{\theta=0}^{\pi / 2} \int_{r=0}^{\sin (\theta)\left(\frac{2}{3}+\frac{1}{3} \cos (40 \phi)\right)} r^{2} \sin (\theta) d r d \theta d \phi=\frac{88}{2835} \pi .\]

(a) valor

(b) error

Figura 12.8: Área de un paralelepípedo.

(a) valor

(b) error

Figura 12.9: Convergencia de la\(\pi\) estimación mediante una integración tridimensional compleja.

Así, podemos estimar el valor de\(\pi\) primero estimando el volumen usando la suma de Montecarlo o Riemann, y luego multiplicando el resultado por\(2835 / 88\).

La figura\(12.9\) muestra el resultado de realizar la integración. La figura muestra que la tasa de convergencia de la suma de Riemann es\(N^{-1 / 3}\), lo cual es consistente con el análisis a priori. Por otro lado, el método Monte Carlo funciona igual de bien que lo hizo para el caso de esfera simple.

\(d\)Dimensiones generales

Generalicemos nuestro análisis al caso de integrar una región\(d\) general-dimensional. En este caso, el método de Monte Carlo considera un\(d\) vector aleatorio\(\left(X_{1}, \ldots, X_{d}\right)\), y asocia con el vector una variable aleatoria de Bernoulli. La convergencia de la integración de Monte Carlo depende de las variables aleatorias de Bernoulli y no se ve afectada directamente por el vector aleatorio. En particular, el método de Monte Carlo es ajeno a la longitud del vector, es decir\(d\), a la dimensionalidad del espacio. Debido a que la desviación estándar de la distribución binomial escala como\(N^{-1 / 2}\), todavía esperamos que el método de Monte Carlo converja a la tasa de\(N^{-1 / 2}\) independientemente de\(d\). Así, los métodos de Montecarlo no sufren la llamada maldición de la dimensionalidad, en la que un método se vuelve intratable con el aumento de la dimensión del problema.

Por otro lado, el rendimiento de la suma de Riemann es una función de la dimensión del espacio. En un espacio\(d\) -dimensional, cada pequeño cubo tiene el volumen de\(N^{-1}\), y hay\(N^{\frac{d-1}{d}}\) cubo que se cruzan con el límite de\(D\). Así, el error escala como\[\text { error } \approx N^{\frac{d-1}{d}} N^{-1}=N^{-1 / d} .\] La tasa de convergencia empeora con la dimensión, y este es un ejemplo de la maldición de la dimensionalidad. Si bien la integración de un volumen físico suele estar limitada a tres dimensiones, hay muchos casos en la ciencia y la ingeniería en los que se requiere una integración dimensional superior.

Ejemplo 12.2.4 Integración sobre una hiperesfera

Para demostrar que la convergencia del método Montecarlo es independiente de la dimensión, consideremos la integración de una hiperesfera en el espacio\(d\) dimensional. El volumen de\(d\) -esfera viene dado por\[V_{D}=\frac{\pi^{d / 2}}{\Gamma(n / 2+1)} r^{d},\] donde\(\Gamma\) está la función gamma. Podemos utilizar nuevamente la integración de una\(d\) -esfera para estimar el valor de\(\pi\).

El resultado de estimar el volumen\(d\) -dimensional se muestra en la Figura\(12.10\) para\(d=2,3,5,7\). La gráfica de convergencia de errores muestra que el método converge a la tasa de\(N^{-1 / 2}\) para todos\(d\). El resultado confirma que la integración de Monte Carlo es un método poderoso para integrar funciones en espacios de dimensiones superiores.

(a) valor

(b) error

Figura 12.10: Convergencia de la\(\pi\) estimación mediante el método de Monte Carlo sobre hiperspheres\(d\) dimensionales.