20: Motivación

Aunque los robots móviles que operan en ambientes planos e interiores a menudo pueden funcionar bastante bien sin ninguna suspensión, en terrenos irregulares, una suspensión bien diseñada puede ser crítica.

Una suspensión de robot real y su modelo simplificado se muestran en la Figura 20.1. Los resortes traseros y delanteros con constantes de resorte\(k_{1}\) y\(k_{2}\) sirven para desacoplar el resto del chasis del robot de las ruedas, permitiendo que el chasis y cualquier instrumentación adjunta “floten” relativamente imperturbables mientras las ruedas permanecen libres para seguir el terreno y mantener la tracción. Los amortiguadores traseros y delanteros con coeficientes de amortiguación\(c_{1}\) y\(c_{2}\) (mostrados aquí dentro de los resortes) disipan energía para evitar desplazamientos excesivos del chasis (por ejemplo, de excitación de un modo resonante) y oscilaciones. Tenga en cuenta que en nuestro modelo de “medio robot”, da\(k_{1}\) cuenta de la rigidez combinada de ambas ruedas traseras, y\(k_{2}\) da cuenta de la rigidez combinada de ambas ruedas delanteras. De igual manera,\(c_{1}\) y dar\(c_{2}\) cuenta de los coeficientes de amortiguación combinados de ambas ruedas traseras y de ambas ruedas delanteras, respectivamente.

Nos preocupa especialmente la posibilidad de que las ruedas delanteras o traseras pierdan contacto con el suelo, cuyas consecuencias -pérdida de control y un aterrizaje potencialmente duro deseamos evitar-.

Para ayudar en nuestra comprensión de las suspensiones de robots y, en particular, para comprender las condiciones que resultan en la pérdida de contacto, deseamos desarrollar una simulación basada en el modelo simple de la Figura 20.1 (b). Específicamente, deseamos simular la respuesta transitoria (tiempo) del robot con suspensión viajando a cierta velocidad constante\(v\) sobre una superficie con perfil\(H(x)\), la altura del suelo en función de\(x\), y verificar si se produce pérdida de contacto. Para ello, debemos integrar las ecuaciones diferenciales de movimiento para el sistema.

Primero, determinamos el movimiento en las ruedas traseras (subíndice 1) y delanteras (subíndice 2) para calcular las fuerzas normales\(N_{1}\) y\(N_{2}\). Debido a que asumimos velocidad constante\(v\), podemos determinar la posición en\(x\) del centro de masa en cualquier momento\(t\) (asumimos\(X(t=0)=0\)) como\[X=v t \text {. }\] Dado el estado actual\(Y, \dot{Y}, \theta\) (la inclinación del chasis) , y\(\dot{\theta}\), entonces podemos calcular el

a) Suspensión real del robot.

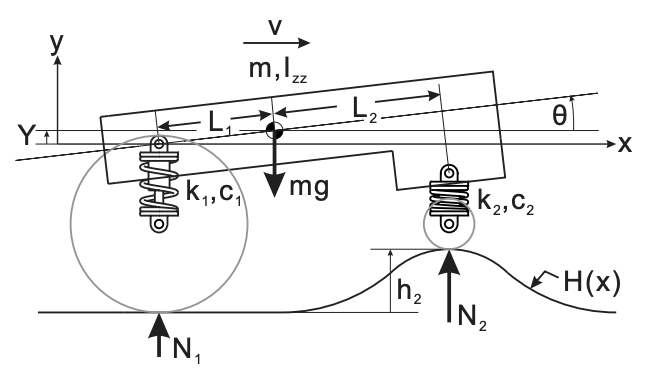
(b) Modelo de suspensión de robot.

Figura 20.1: Suspensión de robot móvil

posiciones y velocidades en ambas\(x\) y\(y\) en las ruedas traseras y delanteras (asumiendo que\(\theta\) es pequeña) como\[\begin{aligned} &X_{1}=X-L_{1}, \quad\left(\dot{X}_{1}=v\right) \\ &X_{2}=X+L_{2}, \quad\left(\dot{X}_{2}=v\right) \\ &Y_{1}=Y-L_{1} \theta \\ &\dot{Y}_{1}=\dot{Y}-L_{1} \dot{\theta} \\ &Y_{2}=Y+L_{2} \theta \\ &\dot{Y}_{2}=\dot{Y}+L_{2} \dot{\theta} \end{aligned}\] dónde\(L_{1}\) y\(L_{2}\) son las distancias al centro de masa del sistema desde las ruedas traseras y delanteras. (Recordar 'se refiere a la derivada del tiempo.) Tenga en cuenta que definimos\(Y=0\) como la altura del centro de masa del robot con ambas ruedas en contacto con el suelo plano y ambos resortes en sus longitudes sin estirar y sin comprimir, es decir, cuándo\(N_{1}=N_{2}=0\). A continuación, determinamos las alturas del suelo en los puntos de contacto trasero y frontal como\[\begin{aligned} &h_{1}=H\left(X_{1}\right) \\ &h_{2}=H\left(X_{2}\right) \end{aligned}\] De manera similar, las tasas de cambio de la altura del suelo en la parte trasera y delantera están dadas por\[\begin{aligned} \frac{d h_{1}}{d t} &=\dot{h}_{1}=v \frac{d}{d x} H\left(X_{1}\right) \\ \frac{d h_{2}}{d t} &=\dot{h}_{2}=v \frac{d}{d x} H\left(X_{2}\right) \end{aligned}\] Tenga en cuenta que debemos multiplicar las derivadas espaciales\(\frac{d H}{d x}\) por\(v=\frac{d X}{d t}\) para encontrar las derivadas temporales.

Mientras las ruedas están en contacto con el suelo podemos determinar las fuerzas normales en la parte trasera y delantera a partir de las ecuaciones constitutivas para los resortes y amortiguadores como\[\begin{aligned} &N_{1}=k_{1}\left(h_{1}-Y_{1}\right)+c_{1}\left(\dot{h}_{1}-\dot{Y}_{1}\right) \\ &N_{2}=k_{2}\left(h_{2}-Y_{2}\right)+c_{2}\left(\dot{h}_{2}-\dot{Y}_{2}\right) \end{aligned}\] Si cualquiera\(N_{1}\) o\(N_{2}\) se calcula a partir de Ecuaciones\((20.5)\) para ser menor que o igual a cero, podemos determinar que la rueda respectiva ha perdido contacto con el suelo y detener la simulación, concluyendo la pérdida de contacto, es decir, falla.

Finalmente, podemos determinar las tasas de cambio del estado a partir del linealizado\((\cos \theta \approx 1\),\(\sin \theta \approx \theta\)) ecuaciones de movimiento para el robot, dadas por Newton-Euler como\[\begin{aligned} \ddot{X} &=0, \quad \dot{X}=v, \quad X(0)=0, \\ \ddot{Y} &=-g+\frac{N_{1}+N_{2}}{m}, \quad \dot{Y}(0)=\dot{Y}_{0}, \quad Y(0)=Y_{0}, \\ \ddot{\theta} &=\frac{N_{2} L_{2}-N_{1} L_{1}}{I_{z z}}, \quad \dot{\theta}(0)=\dot{\theta}_{0}, \quad \theta(0)=\theta_{0}, \end{aligned}\] dónde\(m\) está la masa del robot, y\(I_{z z}\) es el momento de inercia de el robot alrededor de un eje paralelo al\(Z\) eje que pasa por el centro de masa del robot.

En esta unidad discutiremos los procedimientos numéricos mediante los cuales integrar sistemas de ecuaciones diferenciales ordinarias como\(\underline{(20.6)}\). Esta integración puede entonces permitirnos determinar la pérdida de contacto y, por lo tanto, el fracaso.