29.4: Continuación y Homotopía

A menudo nos interesa no resolver un solo problema no lineal, sino más bien una familia de problemas no lineales\(\boldsymbol{f}(\boldsymbol{Z} ; \mu)=\mathbf{0}\) con parámetros reales\(\mu\) que pueden tomar una secuencia de valores\(\mu_{(1)}, \ldots, \mu_{(p)}\). Por lo general, complementamos\(\boldsymbol{f}(\boldsymbol{Z} ; \mu)=0\) con algunas restricciones simples o condiciones de continuidad que seleccionan una solución particular de varias soluciones posibles.

Deseamos entonces asegurar que,\((i)\) seamos capaces de comenzar en absoluto, muchas veces transformando el problema inicial para\(\mu=\mu_{(1)}\) (y quizás también problemas posteriores para\(\mu=\mu_{(i)}\)) en una serie de problemas más simples (homotopía) y, (ii) una vez iniciado, y como parámetro \(\mu\)es variada, seguimos convergiendo para “corregir” soluciones definidas por nuestras limitaciones y condiciones de continuidad (continuación).

Problemas no lineales parametrizados: un solo parámetro

Dado\(\boldsymbol{f}(\boldsymbol{Z} ; \mu)=0\) con un solo parámetro real\(\mu\), normalmente estamos interesados en cómo\(\boldsymbol{Z}\) cambia nuestra solución a medida que cambiamos\(\mu\); en particular, ahora interpretamos (à la teorema de la función implícita)\(\boldsymbol{Z}\) como una función \(\boldsymbol{Z}(\mu)\). Podemos visualizar esta dependencia trazando\(Z\) (aquí\(n=1\)) con respecto a\(\mu\), dándonos un diagrama de bifurcación del problema, como se representa en la Figura\(29.7\) para varios modos comunes de comportamiento.

La Figura 29.7 (a) representa dos ramas de solución aisladas con dos soluciones reales distintas en todo el rango de\(\mu\). La Figura 29.7 (b) representa dos ramas de solución que convergen en un punto singular, donde un cambio en\(\mu\) puede conducir la solución a cualquiera de las dos ramas. La Figura 29.7 (c) representa dos ramas de solución que convergen en un punto límite, más allá del cual no hay solución.

a) Ramas aisladas

b) punto singular

c) punto límite

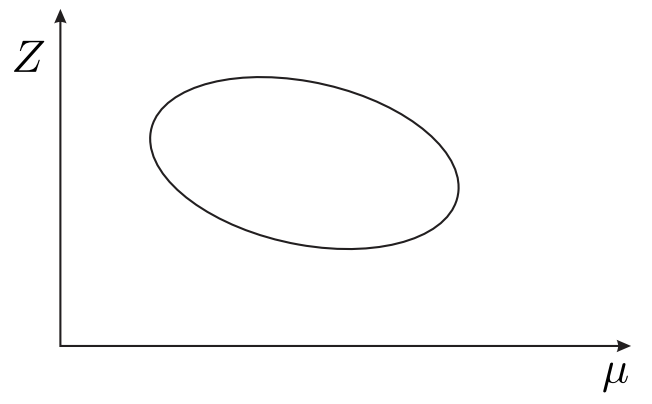
d) isola

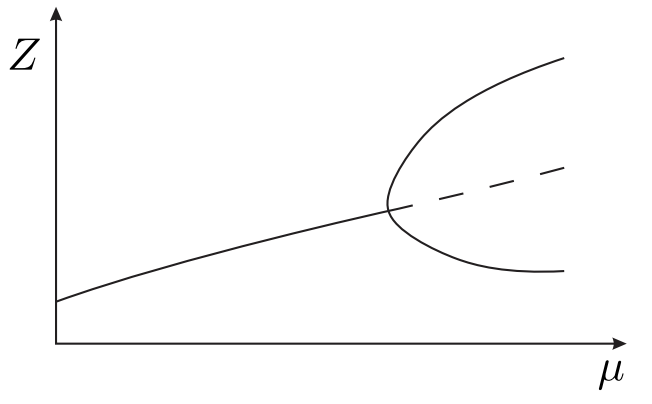
e) horca

Figura 29.7: Diagrama de bifurcación: varios modos comunes de comportamiento.

Figura 29.8: Varillaje mecánico simple.

La Figura 29.7 (d) representa una isola, un intervalo aislado de dos ramificaciones de solución con dos puntos límite para puntos finales. La figura\(29.7(\mathrm{e})\) representa una sola rama de solución que se “bifurca” en varias soluciones en una horca; las bifurcaciones de horca a menudo corresponden a dinámicas no lineales que pueden mostrar un comportamiento estable (representado por líneas continuas en la figura) o inestable (representado por líneas punteadas), donde estabilidad se refiere a la capacidad de la variable de estado\(\boldsymbol{Z}\) para regresar a la solución cuando se perturbe.

Nótese que, para todos los casos mencionados, cuando alcanzamos un punto singular o límite -caracterizado por la convergencia de ramas de solución- el jacobiano se vuelve singular (no invertible) y por lo tanto Newton se descompone a menos que se complemente con condiciones adicionales.

Ejemplo Simple

Podemos desarrollar una comprensión intuitiva de estos diferentes modos de comportamiento y diagramas de bifurcación correspondientes considerando un ejemplo simple.

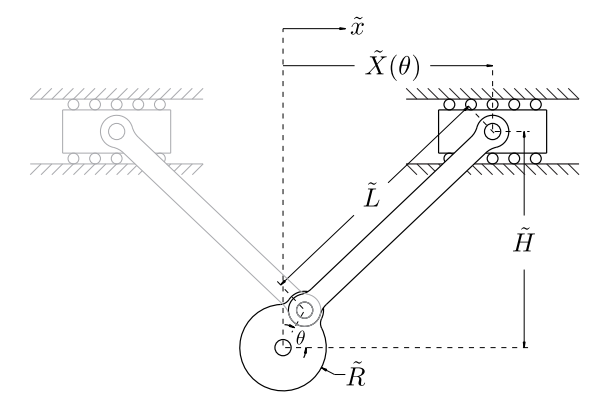
Deseamos analizar el enlace mecánico simple que se muestra en la Figura\(29.8\) encontrando\(\widetilde{X}\) correspondiente a un arbitrario\(\theta\) para dado (constante)\(\widetilde{H}, \widetilde{R}\), y\(\widetilde{L}\). En este ejemplo, entonces,\(\theta\) corresponde al parámetro genérico discutido anteriormente\(\mu\).

Podemos encontrar una solución analítica para\(\widetilde{X}(\theta ; \widetilde{R}, \widetilde{H}, \widetilde{L})\) resolviendo la restricción geométrica\[(\widetilde{X}-\widetilde{R} \cos \theta)^{2}+(\widetilde{H}-\widetilde{R} \sin \theta)^{2}=\widetilde{L}^{2},\] que define la distancia entre las dos juntas como\(\widetilde{L}\). Esta es claramente una ecuación no lineal, debido al término cuadrático en\(\tilde{x}\). Podemos eliminar un parámetro de la ecuación al no dimensionalizar con respecto a\(\widetilde{L}\), dándonos\[(X-R \cos \theta)^{2}+(H-R \sin \theta)^{2}=1,\] dónde\(X=\frac{\tilde{X}}{\tilde{L}}, R=\frac{\tilde{R}}{\tilde{L}}\), y\(H=\frac{\tilde{H}}{\tilde{L}}\). Ampliando y simplificando, obtenemos\[a X^{2}+b X+c \equiv f(X ; \theta ; R, H)=0,\] dónde\(a=1, b=-2 R \cos \theta\), y\(c=R^{2}+H^{2}-2 H R \sin \theta-1\). Una aplicación directa de la fórmula cuadrática nos da entonces las dos raíces\[\begin{aligned} &X_{+}=\frac{-b+\sqrt{b^{2}-4 a c}}{2 a}, \\ &X_{-}=\frac{-b-\sqrt{b^{2}-4 a c}}{2 a}, \end{aligned}\] que pueden ser reales o complejas.

Observamos tres categorías para el número de soluciones a nuestra ecuación cuadrática dependiendo del valor del discriminante\(\Delta(\theta ; R, H) \equiv b^{2}-4 a c\). Primero, si\(\Delta<0, \sqrt{\Delta}\) es imaginario y no hay solución (real). Un ejemplo es el caso en el que\(\widetilde{H}>\widetilde{L}+\widetilde{R}\). Segundo, si\(\Delta=0\), hay exactamente una solución,\(X=\frac{-b}{2 a}\). Un ejemplo es el caso en el que\(\widetilde{H}=\widetilde{L}+\widetilde{R}\) y\(\theta=\frac{\pi}{2}\). Tercero, si\(\Delta>0\), hay dos soluciones distintas,\(X_{+}\) y\(X_{-}\); en la Figura 29.8 se muestra un ejemplo. Tenga en cuenta que con nuestro sencillo ejemplo de manivela podemos obtener todas las cajas de la Figura 29.7 excepto la Figura 29.7 (e).

Observamos que el caso de dos soluciones distintas es nuevo: nuestros sistemas lineales de ecuaciones (para el caso univariado, tampoco\(f(x)=A x-b)\) tuvieron solución (\(A=0, b \neq 0\); línea paralela al\(x\) eje), exactamente una solución (\(A \neq 0\); línea que se cruza \(x\)eje), o un número infinito de soluciones\((A=0\),\(b=0\); línea sobre\(x\) eje). Las ecuaciones no lineales, en cambio, no tienen tales restricciones. No pueden tener solución, una solución, dos soluciones (como en nuestro caso cuadrático anterior), tres soluciones (por ejemplo, una ecuación cúbica) -cualquier número finito de soluciones, dependiendo de la naturaleza de la función particular\(f(z)\) - o un número infinito de soluciones (por ejemplo, una ecuación sinusoidal). Por ejemplo, si\(f(z)\) es un polinomio de\(n^{\text {th }}\) orden -orden, podría haber en cualquier lugar desde cero hasta soluciones\(n\) (reales), dependiendo de los valores de los\(n+1\) parámetros del polinomio.

Es importante señalar, para los casos en los que hay dos, distintas ramas de solución correspondientes\(X_{+}\) y\(X_{-}\), que, a medida que cambiemos la\(\theta\) de la manivela, sería físicamente imposible saltar de una rama a otra -a menos que paráramos el mecanismo, lo desmontó físicamente, y luego lo volvió a ensamblar como una imagen especular de sí misma. Así, para la solución físicamente relevante debemos requerir una condición de continuidad, o equivalentemente una restricción que requiera\(\left|X\left(\theta_{(i)}\right)-X\left(\theta_{(i-1)}\right)\right|\) no demasiado grande o quizás\(X\left(\theta_{(i)}\right) X\left(\theta_{(i-1)}\right)>0\); aquí\(\theta_{(i)}\) y\(\theta_{(i-1)}\) son parámetros sucesivos en nuestra familia de soluciones.

En la Introducción, Sección 29.1, brindamos un ejemplo de vinculación con dos grados de libertad. En este ejemplo de brazo de robot el parámetro\(\boldsymbol{\mu}\) viene dado por\(\boldsymbol{X}\), la posición deseada del efector final.

Siguiendo el camino: Continuación

Como ya se indicó, como variamos nuestro parámetro\(\mu\) (correspondiente\(\theta\) en el ejemplo de manivela), debemos reflejar cualquier restricción (como, en el ejemplo de la manivela, no “re-ensamblaje”) en nuestro enfoque numérico para asegurar que la solución a la que convergimos sea efectivamente la “correcta” “uno. Un enfoque es a través de una elección apropiada de conjetura inicial. Inherente a este imperativo es una oportunidad: podemos explotar la información sobre nuestra solución previamente convergente no solo para mantenernos en la rama de solución adecuada, sino también para ayudar a la convergencia continua (rápida) de la iteración de Newton.

Denotamos nuestra solución previamente convergente a\(f(Z ; \mu)=0\) como\(Z\left(\mu_{(i-1)}\right)\) (consideramos aquí el caso univariado). Deseamos elegir una suposición inicial\(\widehat{Z}\left(\mu_{(i)}\right)\) para converger (una raíz cercana)\(Z\left(\mu_{(i)}\right)=Z\left(\mu_{(i-1)}+\delta \mu\right)\) para algún paso\(\delta \mu\) adentro\(\mu\). El enfoque más simple es utilizar la propia solución previamente convergente como nuestra suposición inicial para el siguiente paso,\[\widehat{Z}\left(\mu_{(i)}\right)=Z\left(\mu_{(i-1)}\right) .\] Esto suele ser suficiente para pequeños cambios\(\delta \mu\) en\(\mu\) y sin duda es el enfoque más simple.

Podemos mejorar nuestra conjetura inicial si utilizamos nuestro conocimiento de la tasa de cambio de\(Z(\mu)\) con respecto a para ayudarnos\(\mu\) a extrapolar, a saber\[\widehat{Z}\left(\mu_{(i)}\right)=Z\left(\mu_{(i-1)}\right)+\frac{\mathrm{d} Z}{\mathrm{~d} \mu} \delta \mu .\] Podemos calcular fácilmente\(\frac{\mathrm{d} Z}{\mathrm{~d} \mu}\) como\[\frac{\mathrm{d} Z}{\mathrm{~d} \mu}=\frac{-\frac{\partial f}{\partial \mu}}{\frac{\partial f}{\partial z}}\] ya\[f(Z(\mu) ; \mu)=0 \Rightarrow \frac{\mathrm{d} f}{\mathrm{~d} \mu}(Z(\mu) ; \mu) \equiv \frac{\partial f}{\partial z} \frac{\mathrm{d} Z}{\mathrm{~d} \mu}+\frac{\partial f}{\partial \mu} \frac{\mathrm{d} f^{\prime}}{d \mu}=0 \Rightarrow \frac{\mathrm{d} Z}{\mathrm{~d} \mu}=\frac{-\frac{\partial f}{\partial \mu}}{\frac{\partial f}{\partial z}}\] por la regla de la cadena.

Arranque en Frío: Homotopía

En muchos casos, dada una solución previa\(Z\left(\mu_{(i-1)}\right)\), podemos usar cualquiera de las ecuaciones (29.63) o (29.64) para llegar a una suposición educada\(\widehat{Z}\left(\mu_{(i)}\right)\) para el parámetro actualizado\(\mu_{(i)}\). Si no tenemos solución previa, sin embargo, (e.g.,\(i=1\)) o nuestras técnicas de continuación fallan, necesitamos algún otro medio para generar una suposición inicial\(\widehat{Z}\left(\mu_{(i)}\right)\) que sea lo suficientemente buena para converger hacia una solución correcta.

Un enfoque común al problema del “arranque en frío” es transformar el problema no lineal original\(f\left(Z\left(\mu_{(i)}\right) ; \mu_{(i)}\right)=0\) en una forma\(\tilde{f}\left(Z\left(\mu_{(i)}, t\right) ; \mu_{(i)}, t\right)=0\), es decir, reemplazamos\(f\left(Z ; \mu_{(i)}\right)=0\) con\(\tilde{f}\left(\widetilde{Z} ; \mu_{(i)}, t\right)=0\). Aquí\(t\) hay un parámetro adicional, artificial, de continuación tal que, cuando\(t=0\), la solución del problema no lineal\[\tilde{f}\left(\widetilde{Z}\left(\mu_{(i)}, t=0\right) ; \mu_{(i)}, t=0\right)=0\] es relativamente simple (por ejemplo, lineal) o, tal vez, coincide con una solución anterior conocida, y, cuando\(t=1\), \[\tilde{f}\left(z ; \mu_{(i)}, t=1\right)=f\left(z ; \mu_{(i)}\right)\]tal que\(\tilde{f}\left(\tilde{Z}\left(\mu_{(i)}, t=1\right) ; \mu_{(i)}, t=1\right)=0\) implica\(f\left(\tilde{Z}\left(\mu_{(i)}\right) ; \mu_{(i)}\right)=0\) y por lo tanto\(Z\left(\mu_{(i)}\right)\) (la solución deseada\()=\widetilde{Z}\left(\mu_{(i)}, t=1\right)\).

Transformamos así el problema del “arranque en frío” en un problema de continuación en el parámetro artificial\(t\) ya que\(t\) se varía de 0 a 1 con un inicio propio (cuando\(t=0\)) hecho significativamente menos “frío” por su -por construcción- relativa simplicidad, y una fin (cuando\(t=1\)) eso nos lleva sin problemas a la solución del problema original de “arranque en frío”.

Como ejemplo, podríamos reemplazar la función\(f\) de manivela de\((29.61)\) por una función\(\tilde{f}(X ; \theta, t ; R, H)=\) en\(X^{2}+b X+c\) tal que para\(t=0\) el problema sea lineal y la solución se obtenga fácilmente.

Aproximación general a la trayectoria: muchos parámetros

Consideramos ahora un\(n\) -vector de funciones\[\boldsymbol{f}(\boldsymbol{z} ; \boldsymbol{\mu})=\left(\begin{array}{llll} f_{1}(\boldsymbol{z} ; \boldsymbol{\mu}) & f_{2}(\boldsymbol{z} ; \boldsymbol{\mu}) & \ldots & f_{n}(\boldsymbol{z} ; \boldsymbol{\mu}) \end{array}\right)^{\mathrm{T}}\] que depende de un\(n\) -vector de incógnitas\(\boldsymbol{z}\)\[\boldsymbol{z}=\left(\begin{array}{llll} z_{1} & z_{2} & \ldots & z_{n} \end{array}\right)^{\mathrm{T}}\] y un parámetro\(\ell\) -vector\(\boldsymbol{\mu}\) (independiente de\(\boldsymbol{z}\))\[\boldsymbol{\mu}=\left(\begin{array}{llll} \mu_{1} & \mu_{2} & \cdots & \mu_{\ell} \end{array}\right)^{\mathrm{T}} .\] También introducir una función de restricción de desigualdad\[C(\boldsymbol{Z})= \begin{cases}1 & \text { if constraint satisfied } \\ 0 & \text { if constraint not satisfied }\end{cases}\] Tenga en cuenta que esto no es una restricción\(\boldsymbol{z}\), sino más bien una restricción en la raíz (deseada)\(\boldsymbol{Z}\). Entonces, dado\(\boldsymbol{\mu}\), buscamos\(\boldsymbol{Z}=\left(\begin{array}{llll}Z_{1} & Z_{2} & \ldots & Z_{n}\end{array}\right)^{\mathrm{T}}\) tal que\[\left\{\begin{array}{l} \boldsymbol{f}(\boldsymbol{Z} ; \boldsymbol{\mu})=\mathbf{0} \\ C(\boldsymbol{Z})=1 \end{array}\right.\] En palabras,\(\boldsymbol{Z}\) sea una solución de ecuaciones\(n\) no lineales en sujetos\(n\) incógnitas que satisfaga la restricción\(C\).

Ahora consideramos una ruta o “trayectoria”, una secuencia de vectores de\(p\) parámetros\(\boldsymbol{\mu}_{(1)}, \ldots, \boldsymbol{\mu}_{(p)}\). Deseamos determinar\(\boldsymbol{Z}_{(i)}, 1 \leq i \leq p\), de tal manera que\[\left\{\begin{array}{l} \boldsymbol{f}\left(\boldsymbol{Z}_{(i)} ; \boldsymbol{\mu}_{(i)}\right)=\mathbf{0} \\ C\left(\boldsymbol{Z}_{(i)}\right)=1 \end{array}\right.\] supongamos que\(\boldsymbol{Z}_{(1)}\) se sabe y que\(\boldsymbol{Z}_{(2)}, \ldots, \boldsymbol{Z}_{(p)}\) quedan por determinar. Podemos esperar, entonces, que mientras los vectores de parámetros consecutivos\(\boldsymbol{\mu}_{(i-1)}\) y\(\boldsymbol{\mu}_{(i)}\) estén lo suficientemente cerca, deberíamos ser capaces de utilizar nuestras ecuaciones de técnicas de continuación\((29.63)\) o\((29.64)\) para converger a una correcta (es decir, satisfactoria \(C\left(\boldsymbol{Z}_{(i)}\right)=1\)) solución\(\boldsymbol{Z}_{(i)}\). Si, sin embargo,\(\boldsymbol{\mu}_{(i-1)}\) y no\(\boldsymbol{\mu}_{(i)}\) estamos lo suficientemente cerca, nuestras técnicas de continuación no serán suficientes (es decir, no convergeremos a una solución en absoluto o no convergeremos a una solución satisfactoria\(C\)) y tendremos que aplicar un - nosotros espero más homotopía a prueba de fallas.

Así, podemos combinar nuestros marcos de continuación y homotopía en un solo algoritmo. Uno de esos enfoques se resume en el Algoritmo 4. Los puntos clave de este algoritmo son que\((i)\) estamos usando el enfoque de continuación simple dado por la ecuación (29.63) (es decir, usando la solución anterior como suposición inicial para el problema actual), y (ii) estamos usando una homotopía de tipo bisección que, cada vez que Newton no converge a un solución correcta, inserta un nuevo punto en la trayectoria a medio camino entre la solución correcta anterior y el punto fallido. Este último, en el lenguaje de la homotopía, se puede expresar como\[\tilde{\boldsymbol{f}}\left(\boldsymbol{z} ; \boldsymbol{\mu}_{(i)}, t\right)=\boldsymbol{f}\left(\boldsymbol{z} ;(1-t) \boldsymbol{\mu}_{(i-1)}+t \boldsymbol{\mu}_{(i)}\right)\] con\(t=0.5\) para el punto insertado.

Aunque existen muchos otros enfoques para la no convergencia además del Algoritmo 4, como el relajado Newton -en el que Newton proporciona la dirección para la actualización, pero luego tomamos solo una pequeña fracción del paso propuesto- El algoritmo 4 se incluye principalmente por su generalidad, simplicidad, y aparente robustez.