10.2: La media muestral - Un estimador/ estimación

Ilustremos la idea de la media muestral en términos de un experimento de volteo de monedas, en el que una moneda es volteada$n$ veces. A diferencia de los casos anteriores, la moneda puede ser injusta, es decir, la probabilidad de cabezas$\theta$,, puede no ser igual a$1 / 2$. Suponemos que no conocemos el valor de$\theta$, y deseamos estimar a$\theta$ partir de los datos recopilados a través de volteretas de$n$ monedas. En otras palabras, se trata de un problema de estimación de parámetros, donde se encuentra el parámetro desconocido$\theta$. Si bien este capítulo sirve como requisito previo para los capítulos de subsecuencia sobre los métodos de Montecarlo -en los que aplicamos conceptos probabilísticos para calcular áreas y más generalmente integrales-, de hecho el capítulo actual se centra en cómo podríamos deducir parámetros físicos a partir de mediciones ruidosas. En definitiva, las estadísticas pueden aplicarse ya sea a cantidades físicas tratadas como variables aleatorias o a cantidades deterministas que se reinterpretan como aleatorias (o pseudoaleatorias).

Al igual que en el capítulo anterior, asociamos el resultado de$n$ flips con un vector aleatorio consistente en variables aleatorias de Bernoulli$n$ i.i.d., $$\left(B_{1}, B_{2}, \ldots, B_{n}\right),$$ donde cada una$B_{i}$ toma el valor de 1 con probablemente de$\theta$ y 0 con probabilidad de$1-\theta$. Las variables aleatorias son i.i.d. porque el resultado de un flip es independiente de otro flip y estamos usando la misma moneda.

Definimos la media muestral de los volteos de$n$ monedas como $$\bar{B}_{n} \equiv \frac{1}{n} \sum_{i=1}^{n} B_{i},$$ que es igual a la fracción de volteretas que son cabezas. Debido a que$\bar{B}_{n}$ es una transformación (es decir, suma) de variables aleatorias, también es una variable aleatoria. Intuitivamente, dado un gran número de volteos, “esperamos” que la fracción de volteos que son cabezas -la frecuencia de las cabezas- se acerque a la probabilidad de una cabeza,$\theta$, por$n$ suficientemente grande. Por esta razón, la media muestral es nuestro estimador en el contexto de la estimación de parámetros. Debido a que el estimador estima el parámetro$\theta$, lo denotaremos por$\widehat{\Theta}_{n}$, y viene dado por $$\widehat{\Theta}_{n}=\bar{B}_{n}=\frac{1}{n} \sum_{i=1}^{n} B_{i} .$$ Note que la media muestral es un ejemplo de una estadística -una función de una muestra que devuelva una variable aleatoria- que, en este caso, se pretende estimar la parámetro$\theta$.

Deseamos estimar el parámetro a partir de una realización particular de volteos de monedas (es decir, una realización de nuestra muestra aleatoria). Para cualquier realización particular, calculamos nuestra estimación como $$\hat{\theta}_{n}=\hat{b}_{n} \equiv \frac{1}{n} \sum_{i=1}^{n} b_{i},$$ dónde$b_{i}$ está el resultado particular del$i$ -ésimo giro. Es importante señalar que los$b_{i}, i=1, \ldots, n$, son números, cada uno tomando el valor de 0 o 1. Así,$\hat{\theta}_{n}$ es un número y no una distribución (aleatoria). Resumamos las distinciones:

	r.v.?	Descripción
$\theta$	no	Parámetro a estimar que gobierna el comportamiento de la distribución subyacente
$\widehat{\Theta}_{n}$	si	Estimador para el parámetro$\theta$
$\hat{\theta}_{n}$	no	Estimación para el parámetro$\theta$ obtenido de una realización particular de nuestra muestra

En general, cómo$\widehat{\Theta}_{n}$ se distribuye la variable aleatoria -en particular sobre$\theta$ - determina si$\widehat{\Theta}_{n}$ es un buen estimador para el parámetro$\theta$. Un ejemplo de convergencia de$\hat{\theta}_{n}$ a$\theta$ con$n$ se muestra en la Figura 10.1. A medida que$n$ aumenta,$\hat{\theta}$ converge$\theta$ para esencialmente toda realización de$B_{i}$'s Esto se desprende del hecho de que$\widehat{\Theta}_{n}$ es un estimador imparcial de$\theta$ - un estimador cuyo esperado valor es igual al parámetro true. Esto lo probaremos en breve.

Para obtener una mejor comprensión del comportamiento de$\widehat{\Theta}_{n}$, podemos construir la distribución empírica de$\widehat{\Theta}_{n}$ realizando una gran cantidad de experimentos para un dado$n$. Denotemos el número de

Figura 10.1: Convergencia de estimación con$n$ una realización particular de volteretas de monedas.

experimentos por$n_{\exp }$. En el primer experimento, trabajamos con una realización$\left(b_{1}, b_{2}, \ldots, b_{n}\right)^{\exp 1}$ y obtenemos la estimación calculando la media, es decir, de $$\exp 1:\left(b_{1}, b_{2}, \ldots, b_{n}\right)^{\exp 1} \quad \Rightarrow \quad \bar{b}_{n}^{\exp 1}=\frac{1}{n} \sum_{i=1}^{n}\left(b_{i}\right)^{\exp 1} .$$ manera similar, para el segundo experimento, trabajamos con una nueva realización para obtener $$\exp 2:\left(b_{1}, b_{2}, \ldots, b_{n}\right)^{\exp 2} \quad \Rightarrow \quad \bar{b}_{n}^{\exp 2}=\frac{1}{n} \sum_{i=1}^{n}\left(b_{i}\right)^{\exp 2} .$$ Repitiendo los$n_{\exp }$ tiempos del procedimiento, finalmente obtenemos $$\exp n_{\exp }:\left(b_{1}, b_{2}, \ldots, b_{n}\right)^{\exp n_{\exp }} \Rightarrow \bar{b}_{n}^{\exp n_{\exp }}=\frac{1}{n} \sum_{i=1}^{n}\left(b_{i}\right)^{\exp n_{\exp }} .$$ Observamos que$\bar{b}_{n}$ puede tomar cualquier valor$k / n, k=0, \ldots, n$. Podemos calcular la frecuencia de$\bar{b}_{n}$ tomar un cierto valor, es decir, el número de experimentos que produce$\bar{b}_{n}=k / n$.

El resultado numérico de realizar 10,000 experimentos para$n=2,10,100$, y 1000 volteretas se muestran en la Figura 10.2. La distribución empírica de$\widehat{\Theta}_{n}$ espectáculos que con$\widehat{\Theta}_{n}$ mayor frecuencia toma los valores cercanos al parámetro subyacente a$\theta$ medida que aumenta el número de volteretas$n$,,. Así, el experimento numérico confirma que efectivamente$\widehat{\Theta}_{n}$ es un buen estimador de$\theta$ si$n$ es suficientemente grande.

Habiendo visto que nuestra estimación converge al parámetro verdadero$\theta$ en la práctica, ahora analizaremos el comportamiento de convergencia con el parámetro verdadero relacionando la media de la muestra con una distribución binomial. Recordemos, que la distribución binomial representa el número de cabezas obtenidas al voltear una moneda$n$ veces, es decir, si$Z_{n} \sim \mathcal{B}(n, \theta)$, entonces $$Z_{n}=\sum_{i=1}^{n} B_{i},$$ donde$B_{i}, i=1, \ldots, n$, son la variable aleatoria de Bernoulli i.d., que representa el resultado de los volteos de monedas (teniendo cada uno el probabilidad de cabeza de$\theta$). La distribución binomial y la media muestral se relacionan por $$\widehat{\Theta}_{n}=\frac{1}{n} Z_{n}$$

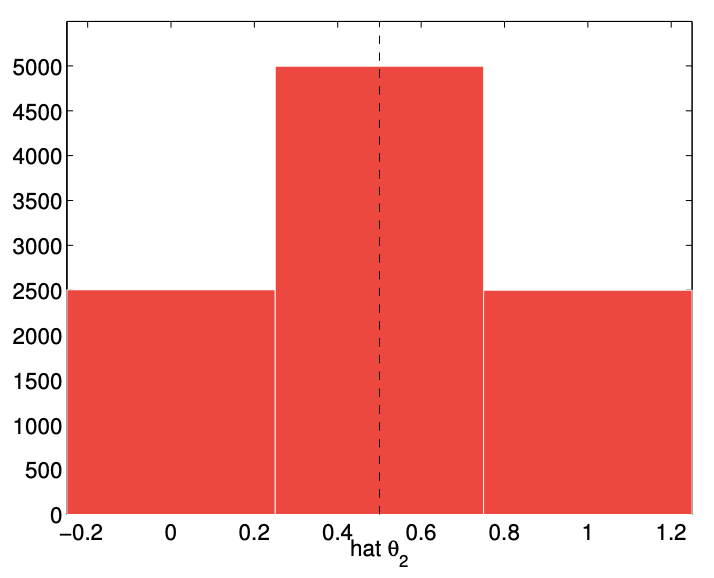
(a)$n=2$

b)$n=10$

c)$n=100$

d)$n=1000$

Figura 10.2: Distribución empírica de$\widehat{\Theta}_{n}$ para$n=2,10,100$, y 1000 y$\theta=1 / 2$ obtenida de 10,000 experimentos.

La media (un parámetro determinista) de la media muestral (una variable aleatoria) es $$E\left[\widehat{\Theta}_{n}\right]=E\left[\frac{1}{n} Z_{n}\right]=\frac{1}{n} E\left[Z_{n}\right]=\frac{1}{n}(n \theta)=\theta .$$ En otras palabras,$\widehat{\Theta}_{n}$ es un estimador imparcial de$\theta$. La varianza de la media $$\begin{aligned} \operatorname{Var}\left[\widehat{\Theta}_{n}\right] &=E\left[\left(\widehat{\Theta}_{n}-E\left[\widehat{\Theta}_{n}\right]\right)^{2}\right]=E\left[\left(\frac{1}{n} Z_{n}-\frac{1}{n} E\left[Z_{n}\right]\right)^{2}\right]=\frac{1}{n^{2}} E\left[\left(Z_{n}-E\left[Z_{n}\right]\right)^{2}\right] \\ &=\frac{1}{n^{2}} \operatorname{Var}\left[Z_{n}\right]=\frac{1}{n^{2}} n \theta(1-\theta)=\frac{\theta(1-\theta)}{n} . \end{aligned}$$ muestral es La desviación estándar de$\widehat{\Theta}_{n}$ es $$\sigma_{\hat{\Theta}_{n}}=\sqrt{\operatorname{Var}\left[\widehat{\Theta}_{n}\right]}=\sqrt{\frac{\theta(1-\theta)}{n}} .$$ Así, la desviación estándar de$\widehat{\Theta}_{n}$ disminuye con$n$, y en particular tiende a cero as$1 / \sqrt{n}$. Esto implica que$\widehat{\Theta}_{n} \rightarrow \theta$ como$n \rightarrow \infty$ debido a que es muy poco probable que$\widehat{\Theta}_{n}$ va a tomar en un valor muchas desviaciones estándar alejadas de la media. En otras palabras, el estimador converge al parámetro verdadero con el número de volteos.