11.3: Incompresibilidad

Numerosos experimentos realizados en el pasado 100% han demostrado que los metales son prácticamente incompresibles en la gama plástica. Exploremos las consecuencias de este hecho físico en el caso del caso unidimensional. Denote la longitud de calibre de la barra prismática por$l$ y su área de sección transversal por$A$. El volumen de corriente de la sección de calibre es$V = Al$. Incompresibilidad significa que el volumen debe estar inalterado o$dV = 0$.

$$dV = d(Al) = dAl + Adl = 0 \label{11.3.1}$$

De la Ecuación\ ref {11.3.1} inferimos que el incremento de deformación se$d\epsilon$ puede calcular ya sea rastreando la longitud del calibre o el área de la sección transversal

$$d\epsilon = \frac{dl}{l} = − \frac{dA}{A} \label{eq0}$$

Integrando la primera parte de la ecuación\ ref {eq0}

$$\epsilon = \ln l + C_1$$

La constante de integración se obtiene al requerir que la deformación se desvanezca cuando la longitud$l$ es igual al calibre inicial, longitud de referencia$l_o$, lo que da$C = − \ln l_o$. Así

$$\epsilon = \ln \frac{l}{l_o} \label{eq1}$$

que es la definición logarítmica de deformación, introducida en el Capítulo 1. Del mismo modo, integrando la segunda parte de la Ecuación\ ref {eq0} con la condición inicial en$A = A_o$,$\epsilon = 0$, se obtiene

$$\epsilon = \ln \frac{A_o}{A} \label{eq2}$$

En tensión$l > l_o$ o$A < A_o$, así ambas Ecuaciones\ ref {eq1} y\ ref {eq2} dan la tensión positiva. En compresión la deformación es negativa. Lo mismo es cierto para los incrementos de deformación$d\epsilon$ o las tasas de deformación

$$\dot{\epsilon} = \frac{\dot{l}}{l} \quad \text{ or } \quad \dot{\epsilon} = − \frac{\dot{A}}{A}$$

Del análisis anterior se desprende una simple extensión de la condición de incompresibilidad plástica en el caso 3-D. Considerar un elemento de volumen infinitesimal$V = x_1x_2x_3$, Figura ($\PageIndex{1}$)

Figura$\PageIndex{1}$: Elementos de volumen 1-D y 3-D no deformados y deformados.

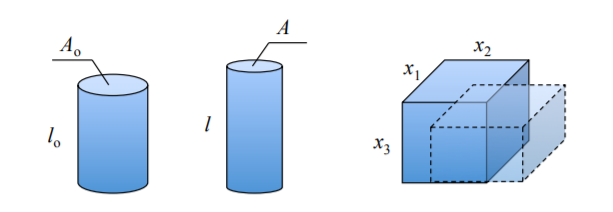
La incompresibilidad plástica requiere que

$$dV = d(x_1x_2x_3) = dx_1(x_2x_3) + x_1d(x_2x_3) \\ = dx_1x_2x_3 + x_1dx_2x_3 + x_1x_2dx_3$$

Dividiendo ambos lados de la ecuación anterior por el volumen, se obtiene

$$\frac{dx_1}{x_1} + \frac{dx_2}{x_2} + \frac{dx_3}{x_3} = 0$$

o

$$d\epsilon_{11} + d\epsilon_{22} + d\epsilon_{33} = 0, \quad d\epsilon_{kk} = 0 \nonumber$$

Señalando que$d\epsilon_{11} = \frac{\partial \epsilon_{11}}{\partial t} dt = \dot{\epsilon}_{11}dt$, una forma alternativa de la condición de incompresibilidad es

$$\dot{\epsilon}_{11} + \dot{\epsilon}_{22} + \dot{\epsilon}_{33} = 0, \quad \dot{\epsilon}_{kk} = 0$$

La suma de los componentes diagonales del tensor de velocidad de deformación debe desvanecerse para asegurar la incompresibilidad. Se deduce de la regla de flujo (a formular posteriormente) que en tensión uniaxial en$x_1$ dirección los componentes$\dot{\epsilon}_{22} = \dot{\epsilon}_{33}$. Por lo tanto$\dot{\epsilon}_{11} + 2\dot{\epsilon}_{22} = 0$ o$\dot{\epsilon}_{11} + 2\dot{\epsilon}_{33} = 0$. Finalmente obtenemos

$$\dot{\epsilon}_{22} = −0.5\dot{\epsilon}_{11}, \quad \dot{\epsilon}_{33} = −0.5\dot{\epsilon}_{11}$$

El coeficiente 0.5 se puede interpretar como la relación de Poisson

$$\nu = − \frac{\dot{\epsilon}_{22}}{\dot{\epsilon}_{11}} = − \frac{\dot{\epsilon}_{33}}{\dot{\epsilon}_{11}} = 0.5$$

Podemos concluir que la incompresibilidad plástica requiere que la relación de Poisson sea igual a$1/2$, que es diferente de la relación elástica de Poisson, igual$\tilde 0.3$ para los metales. Muchos otros materiales como el caucho, los polímeros y el agua son incompresibles.