2: Propulsión

Última actualización
Guardar como PDF

Page ID: 80957

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Introducción

En el Capítulo 1 analizamos la Atmósfera Estándar, el entorno en el que operan los aviones, la ecuación de Bernoulli y su relación con la aerodinámica del avión (o más específicamente, el ala), y algunos parámetros básicos que influyen en el rendimiento aerodinámico de un avión. En este capítulo veremos la forma en que damos cuenta de la propulsión de aviones; es decir, los motores jet o hélices. Esto significa que estaremos viendo los factores que afectan cosas como el empuje y la potencia del avión. También encontraremos que los mismos factores que explican el empuje también se pueden utilizar para dar cuenta de parte del arrastre en un avión.

Al mirar el empuje, el poder y el arrastre nos interesa saber cómo estos pueden variar con la velocidad del avión y con la altitud. Debemos tener una comprensión básica de estas dependencias si vamos a utilizarlas eventualmente para determinar el rendimiento de un avión.

Los motores de avión son, por supuesto, el tema de cursos completos de ingeniería que tratan cosas como los motores de combustión interna y los motores a reacción que respiran aire. Queremos limitarnos a un enfoque muy sencillo para entender cómo funciona la propulsión sin entrar en más detalles de los que son absolutamente necesarios. Afortunadamente, vamos a poder hacer esto.

2.1 Motores a reacción

Los motores a reacción vienen en una amplia gama de diseños. La mayoría son considerados motores de “turbina” porque las turbinas se utilizan para extraer energía del flujo de escape de alta velocidad para impulsar un “compresor” para comprimir el flujo hacia el motor antes de la adición de combustible y la combustión, pero a velocidades muy altas (flujo hipersónico) es posible obtener compresión a través de ondas de choque y un motor a reacción sin turbina llamado “ramjet” es el resultado. No obstante, nos vamos a restringir a vuelos subsónicos e incompresibles donde siempre se necesitan turbinas y compresores.

El tipo más básico de motor a reacción se llama “turborreactor” y consiste básicamente en una entrada, seguido de un compresor que aumenta la presión (y baja la velocidad) del aire antes de que entre en la cámara de combustión donde se agrega combustible y se enciende. Después de la combustión, una turbina extrae suficiente energía de los productos de escape de alta energía (alta velocidad) para impulsar el compresor, y el flujo luego sale a través del escape del motor a alta velocidad para proporcionar empuje.

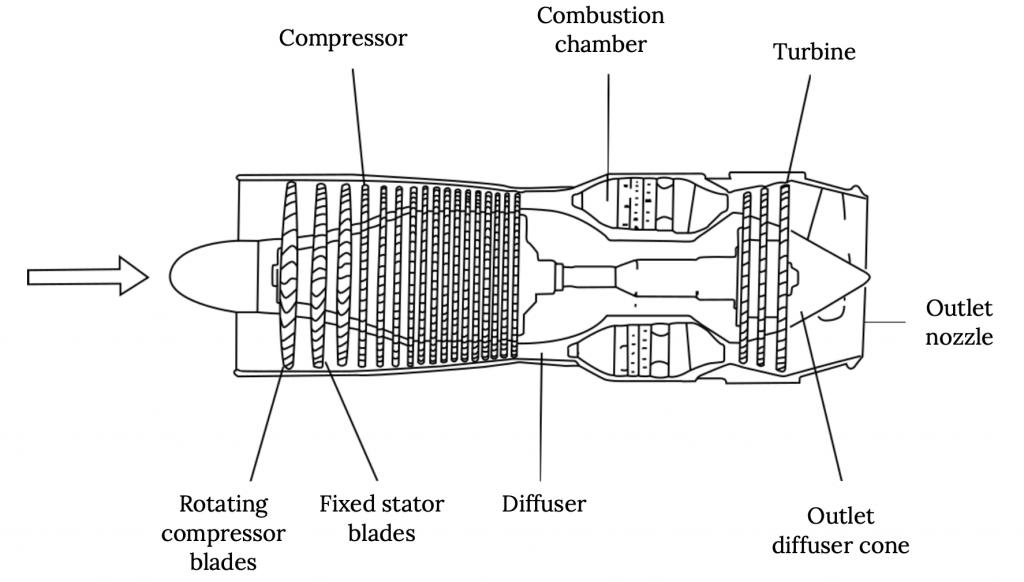
Una sección transversal de un motor turborreactor muestra cómo se ve forzado a espacios cada vez más pequeños. El primer aire entra al motor y pasa por un conjunto de aspas rotativas del compresor. A continuación se mueve a un conjunto de álabes fijos del estator inmediatamente después, antes de continuar en el resto de la sección del compresor, que se estrecha continuamente. Luego, el aire pasa a través de un difusor a una cámara de combustión. Después de la cámara de combustión, pasa a través de una turbina, donde se le permite expandirse, y luego la boquilla de salida, más allá del cono difusor de salida en el centro. — Figura 2.1: Ilustración del motor TurboJet

Resulta que un turborreactor puro no es una forma muy eficiente de hacer empuje. Crea empuje a través de un escape de muy alta velocidad y esto es a la vez muy ruidoso y muy propenso a pérdidas. El chorro de escape de alta velocidad esencialmente se abre paso a través del aire circundante y esta interacción violenta entre el escape y la atmósfera da como resultado muchas pérdidas similares a la fricción y hace mucho ruido.

Veremos la propulsión a chorro en términos de cambios de impulso (energía por unidad de tiempo) con la diferencia entre el impulso en el escape y la entrada del motor que representa el empuje y, a primera vista, parecerá que cualquier forma en que podamos obtener un cambio de impulso es igual de buena como cualquier otra forma, pero eso es no es el caso.

Momentum es esencialmente la masa multiplicada por la velocidad (velocidad). Esto significa que hay dos formas de conseguir un cambio de impulso. Una es tomar una pequeña cantidad de masa y acelerarla a una velocidad muy alta como se hace en un motor turborreactor. Otra es tomar una gran cantidad de masa y acelerarla en una cantidad menor. Al final resulta que esta última forma es la forma más eficiente de conseguir el empuje. Es como comparar los efectos de un ventilador de techo grande que gira lentamente con los de un pequeño ventilador “personal”. Si realizaras dos lanchas neumáticas impulsadas por hélice del tipo que se usa en los pantanos, una embarcación con una hélice pequeña y la otra con una grande, encontrarías que la embarcación con el puntal más grande necesitaría menos potencia para moverse a una velocidad dada que la que tiene el puntal pequeño.

Los jets de ventilador se basan en este principio para proporcionar un empuje más eficiente a un avión que los turborreactores. En un chorro de ventilador, la turbina o turbinas del motor impulsan tanto el compresor que funciona en el aire que entra en la cámara de combustión como un ventilador grande que agrega impulso a una gran masa de aire que rodea el núcleo del motor sin ser utilizado para quemar combustible. Este ventilador o aire “bypass” luego se mezcla con el núcleo de mayor velocidad, productos de combustión para dar un alto impulso de escape total del motor que deriva su impulso de la gran masa del flujo de derivación y la alta velocidad del flujo del núcleo.

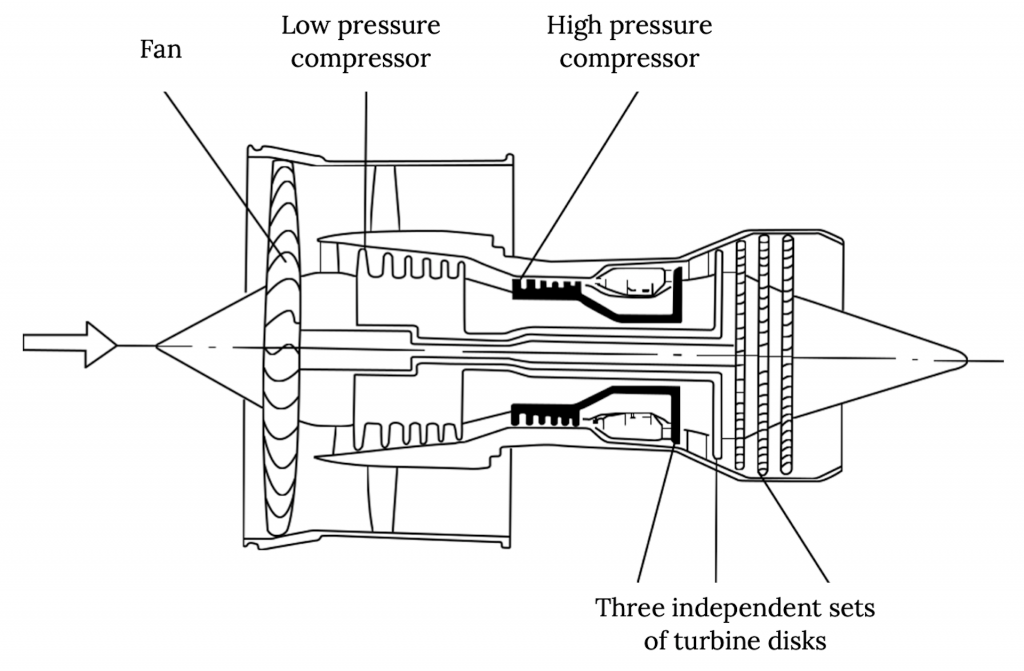
Se muestra una sección transversal para un motor turborreactor de barra de turboventilador. El aire entra más allá del ventilador inicial, con dos trayectorias después: los bordes exteriores pasan por alto el motor por completo y salen de la estructura, y las partes centrales que conducen a un compresor de baja presión, que luego se alimenta a un compresor de alta presión. Después de ambos compresores, el aire baja a través de tres conjuntos independientes de discos de turbina antes de salir por la boquilla en la parte trasera del motor. — Figura 2.2: Ilustración de un Turbo-Ventilador o Motor a Chorro de Ventilador

Entonces, para una cantidad dada de empuje necesitaremos una cantidad dada de cambio de impulso del aire que pasa por el motor entre su entrada y salida. Veremos cómo este cambio de impulso explica matemáticamente el empuje un poco más tarde. El punto aquí es que la forma más eficiente de conseguir este cambio de impulso con pérdidas mínimas es acelerar una gran masa de aire en una pequeña cantidad (pequeño cambio de velocidad). Esto significa que cuanto mayor sea la relación de derivación (la relación entre la masa de aire de derivación y la masa de aire que pasa por el núcleo del motor), más eficiente es el motor. Pero hay un límite para esto.

A medida que el motor a reacción del ventilador se hace más grande debido al diseño de mayor relación de derivación, la carcasa del motor (góndolas) también se hace más grande y produce más resistencia. Entonces en algún momento tiene más sentido reemplazar el “ventilador” de derivación por una hélice grande. El resultado es el motor “turbohélice”.

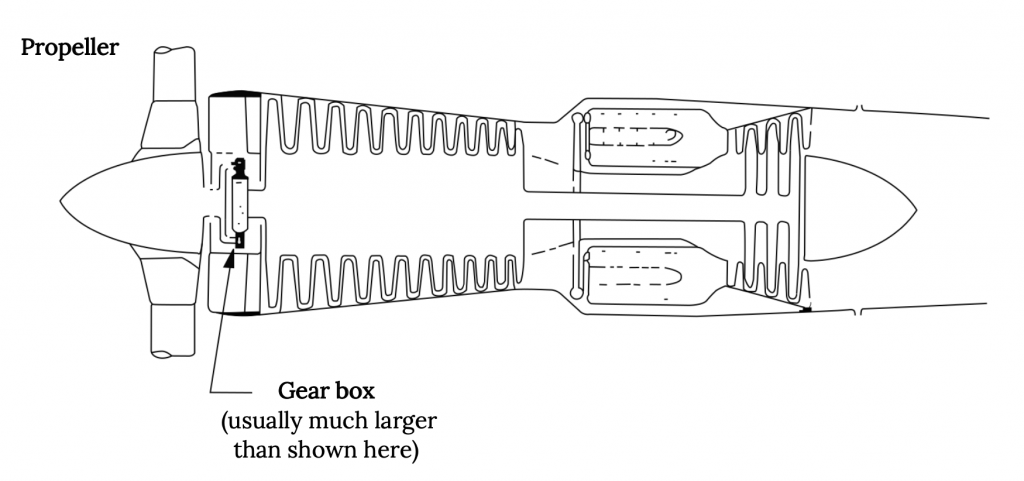
La sección transversal de un motor turbo-hélice muestra la hélice en la parte delantera conectada a una caja de engranajes en el centro. Luego, la caja de engranajes se conecta a aspas adicionales del compresor, cámara de combustión y ventiladores de turbina, pero estos no son la principal fuente de empuje. — Figura 2.3: Ilustración del motor turbopropulsor

En el motor turbohélice el flujo a través del núcleo del motor realmente no se usa para producir ningún empuje significativo. La turbina de escape está diseñada para tomar toda la energía que pueda del escape para impulsar la hélice y todo el empuje del motor proviene del flujo a través de la hélice. En un motor turbohélice la cantidad de empuje que proviene del flujo central es tan insignificante que, en algunos diseños de motores, el flujo del núcleo realmente va “hacia atrás”.

Podríamos preguntarnos, si el motor turbohélice es más eficiente que el fan-jet, que a su vez es más eficiente que el turborreactor, ¿por qué los fan-jets son el motor preferido para la mayoría de los aviones hoy en día? La respuesta está en la velocidad de vuelo deseada.

Así como hay una gran subida de arrastre en un ala a medida que se acerca a la velocidad del sonido, hay pérdidas de tipo arrastre en una pala de hélice cuando su velocidad se acerca a Mach one. De hecho, para una velocidad de rotación de hélice dada, el límite en el diámetro práctico para el puntal está determinado por el radio en el que la sección de la pala de la hélice alcanza su número crítico de Mach. Y, dado que la velocidad aérea que ven las palas de las hélices es función tanto de su velocidad de rotación como de la velocidad del avión, esto limita la velocidad de la aeronave. El diseño de la hélice puede extender este rango de velocidad algo con cosas como puntas de pala barridas, pero el turbohélice siempre impondrá límites a las velocidades de crucero de los aviones

Además, resulta que las velocidades de rotación necesarias para una hélice turbohélice son un orden de magnitud inferiores a las de las de un núcleo de turbina eficiente y esto requiere engranajes de reducción de velocidad entre la turbina y el propulsor y esto introduce tanto ruido como vibraciones que no se encuentran en el chorro de ventilador.

2.2 Motores de Hélice

Entonces, ¿cuál es la diferencia entre un turbohélice y una hélice impulsada por un motor de combustión interna? Desde el punto de vista del empuje proporcionado por la hélice, no hay mucha diferencia. La diferencia está en el motor y el engranajes que impulsa la hélice.

El turbohélice es impulsado por un pequeño motor de turbina (jet) que envía la mayor parte de su energía como sea posible a la hélice a través de un árbol de transmisión y un sistema de engranajes reductores. La hélice del motor IC está unida al eje de transmisión de un motor de combustión interna que, como la mayoría de los motores de automóviles, utiliza la quema de gasolina o combustible diesel en un motor tipo pistón/cilindro para girar el eje.

Hoy la mayoría de los motores de hélice impulsados por combustión interna se encuentran en aviones de aviación general más pequeños Este tipo de motor ha proporcionado una potencia confiable y asequible para los aviones desde el primer vuelo de los hermanos Wright en 1903. A lo largo de los años ha habido muchas variaciones fascinantes del motor IC utilizado en aviones, desde los motores “rotativos” de la Primera Guerra Mundial en los que el eje de transmisión estaba unido al avión y la hélice y el motor realmente giraron juntos alrededor del eje, hasta los enormes motores de pistón de las décadas de 1940 y 1950 con decenas de cilindros dispuestos alrededor del eje de transmisión como granos en una mazorca de maíz, a los cuatro y seis cilindros, tipo automóvil pero refrigerados por aire, motores que generalmente se encuentran en los aviones GA actuales. Estas muchas variedades de motores IC harían un estudio interesante y agotador en sí mismas, pero eso está más allá del alcance de este texto.

En lo que a nosotros nos concierne, un motor de hélice es un motor de hélice, ya sea impulsado por una turbina o un motor IC o una banda de goma. Simplemente nos preocuparemos por la salida de “potencia” del motor y a esto lo llamaremos la “potencia del eje” independientemente del tipo de motor que impulse el eje.

2.3 Empuje y potencia

Esto nos lleva a la principal diferencia en la forma en que hablaremos de propulsión para motores jet y prop. Para aviones a reacción, ya sean turborreactores o fanjets, caracterizaremos las propiedades de propulsión del avión en términos de empuje. Para los aviones propulsados por hélice, ya sea que la hélice esté unida a un motor IC o a una turbina, hablaremos sobre el rendimiento en términos de potencia.

La potencia y el empuje son simplemente dos formas diferentes de ver la propulsión y el rendimiento de los aviones. Están directamente relacionados entre sí a través de la velocidad.

Potencia = (Empuje) (Velocidad)

Si bien normalmente hablamos de propulsión a chorro en términos de empuje y propulsión de hélice en términos de potencia, hay pocas razones más allá de lo convencional para que debamos hacerlo. Podríamos hablar de la potencia de un motor a reacción y el empuje de una hélice y a veces lo hacemos. Quizás una razón de esta distinción es que más adelante nos resultará conveniente observar la variación tanto de la potencia como del empuje con la velocidad y encontraremos que es común suponer que el empuje es bastante constante con la velocidad para un jet y la potencia es bastante constante con la velocidad para un avión impulsado por hélice.

Las unidades normalmente asociadas con la potencia y el empuje, respectivamente, son libras y caballos de fuerza. Sí, se trata de unidades “políticamente incorrectas”; sin embargo, son mucho más utilizadas que Newtons y Watts, sus equivalentes SI. [¿Alguna vez has escuchado a alguien hablar de la potencia del motor de su automóvil en vatios?] Esto, por supuesto, significa que necesitamos aprender cómo la unidad de caballos de fuerza se relaciona con las unidades básicas en el sistema “inglés”.

1 caballo de fuerza = 550 pie-libras/segundo.

[Un poco de trivialidades de ingeniería: esta conversión se usaba tan a menudo en los días de los cálculos de reglas de cálculo que la mayoría de las reglas de cálculo tenían una marca especial en ellas en la ubicación 550 en la diapositiva.]

2.4 Leyes de Empuje y Conservación

Para saber cómo cosas como la altitud y la velocidad del aire afectan el empuje y la potencia necesitamos echar un vistazo a cómo pasa el aire a través de la hélice o el motor a reacción cuando un avión está en vuelo y cómo cambia el impulso del aire a medida que sigue ese camino. Para ello habrá que mirar dos “leyes de conservación”, la conservación de la masa y la conservación del impulso.

2.4.1 Conservación Masiva

En su concepto más simple la conservación de masas se suele afirmar algo así como “la masa no puede ser creada ni destruida; es decir, es constante o conservada”. Esto suele ir acompañado de un calificador señalando que, en una reacción atómica, la masa puede realmente ser creada (reacción de fusión) o destruida (reacción de fisión). Esta es una manera interesante de mirar la masa si uno está mirando la masa en el universo o en un contenedor cerrado pero no nos ayuda a la hora de hablar de motores. Tenemos que mirar la conservación de la masa en un flujo; es decir, en el aire que pasa por una habitación o una tubería o una hélice o un motor a reacción.

Si tuviéramos una habitación sellada llena de aire sería sencillo afirmar que la cantidad de aire en la habitación es una constante. Podríamos tener personas y plantas en la habitación con las reacciones químicas que forman parte de la respiración humana y la química vegetal alterando continuamente las circunscripciones químicas en el “aire”; sin embargo, la masa total del “aire” permanecería constante.

El panorama cambia cuando agregamos ventilación a la habitación, ya sea mediante el uso de un sistema de ventilación forzada como un sistema de aire acondicionado o calefacción o simplemente abriendo ventanas y puertas. Con cualquiera de los sistemas habría aire nuevo entrando en las ventanas, puertas o respiraderos de entrada y aire viejo saliendo de otras ventanas, puertas o respiraderos de escape. Si tuviéramos una habitación con solo una entrada de aire forzado y sin escape, la masa de aire en la habitación aumentaría a medida que el aire entrara por la entrada. Para acomodar esta masa creciente la habitación tendría que expandirse como un globo o la presión y densidad del aire en la habitación tendría que aumentar. Tenga en cuenta que, si asumimos que el aire era “incompresible” sería imposible bombear aire nuevo a la habitación sin proporcionar un escape para que escape una cantidad igual de aire. Esto requeriría conservación en la masa del aire en la habitación.

Entonces, en el ejemplo de la ventilación de la habitación, la conservación de la masa para el aire en la habitación simplemente significaría que, como una masa de aire nuevo ingresa a la habitación, la misma cantidad de masa de aire debe salir de la habitación. Los aires acondicionados de habitación o ventana funcionan de esta manera, tomando un caudal másico dado de la habitación, enviándolo a través de serpentines de enfriamiento y devolviendo ese mismo caudal másico a la habitación después de que se eliminó algo de calor del aire.

Esto nos lleva al tema del caudal másico, a menudo llamado “m-dot” y dado el símbolo de una “m” minúscula con un punto en la parte superior de la letra para representar una derivada de tiempo de la masa; es decir, masa por unidad de tiempo, dm/dt.

Cuando hablamos de una habitación con respiraderos o puertas y ventanas debemos hablar de caudales másticos, y decimos que para tener conservación masiva no debemos tener ningún cambio en la masa dentro de la habitación por unidad de tiempo, simplemente otra forma de decir que la cantidad de masa que entra durante un periodo de tiempo determinado debe ser igual la cantidad de masa que sale en ese mismo tiempo. Esto se afirma como:

dm/dt = 0.

Es decir, la cantidad de masa en la habitación no cambia con el tiempo.

A menudo ponemos esto en forma de ecuación, diciendo que

dm/dt = σ ρ VA = 0.

Aquí, estamos diciendo que el caudal másico es igual a la densidad del aire, multiplicado por su velocidad, ya que pasa por un área de tamaño “A”. Es decir, si el aire a la densidad del nivel del mar está soplando a través de una ventana a una velocidad de 20 pies por segundo y si esa ventana tiene una abertura de 2 pies por 4 pies, podemos calcular la masa de aire por unidad de tiempo que está pasando por la ventana.

dm/dt = ρ VA = (0.002378 sl/ft ³) (20 pies/seg.) (2 pies x 4 pies) = 0.3805 sl/seg.

[Obsérvese aquí que se ha encontrado que las unidades de caudal másico son babosas por segundo. En el sistema SI se encontrarían en kilogramos por segundo y en una versión del sistema “inglés” de uso frecuente en campos como la Ingeniería Mecánica las unidades de caudal másico serían libras-masa por segundo .]

Ahora bien, si se cumple la conservación de la masa para el aire en la habitación, la misma masa de aire por unidad de tiempo debe estar saliendo de otra abertura o aberturas.

(dm/dt) _en + (dm/dt) _fuera = 0

(ρ VA) _en + (ρ VA) _fuera = 0

Entonces, si hay una sola ventana que deja entrar el flujo de aire que se encuentra arriba y la salida es a través de una puerta, podemos utilizar la conservación de la masa para determinar la velocidad del aire que sale por la puerta.

(ρ VA) _fuera = — (ρ VA) _pulg.

Así como tres factores, el tamaño (área) de la ventana, la velocidad del flujo de aire a través de la ventana, y la densidad del aire, determinaron el “caudal másico” del aire que entra en la habitación, las mismas tres cosas determinan el caudal másico de salida. En realidad, las tres cosas podrían ser diferentes en la salida (puerta, en este caso), así que, si queremos encontrar la velocidad del aire que sale debemos conocer tanto el área de la puerta como la densidad del aire en la puerta. Sin embargo, no hay razón por la que el aire que fluye por la habitación hubiera cambiado de densidad por lo que estamos seguros al asumir un flujo “incompresible”, es decir, la densidad es constante. Esto nos da una ecuación simple:

(VA) _fuera = — (VA) _pulg.

Entonces, si la puerta tiene 3 pies de ancho por 7 pies de alto, dando un área de 21 pies ², mientras que la ventana tenía un área de 8 pies ², la velocidad del aire que sale por la puerta es:

V _out /V _in = — A _in /A _out

V _out = — V _in (A _in /A _out)

o en este caso,

V _out = — 20 pies/seg. (8 ft ²/21 ft ²) = — 7.62 pies/seg.

Ahora bien, ¿por qué hay un signo menos con la velocidad de salida? Esto se debe a que nosotros, sin razón real, optamos por dar un sentido positivo a la velocidad que va por la ventana y como la velocidad es un vector; es decir, tiene una dirección, hemos designado como positivo el flujo de aire hacia la habitación. Esto quiere decir que el signo negativo en la velocidad del aire de salida nos dice que está saliendo de la habitación. Si bien esto puede parecer una complicación innecesaria aquí, hay casos en los que puede ayudarnos a descubrir lo que está sucediendo.

Por ejemplo, supongamos que hay cinco ventanas y dos puertas en nuestra habitación y se nos dice que el aire está entrando en las cinco ventanas a cierta velocidad y está saliendo una puerta a una velocidad dada, ¿qué está pasando en la otra puerta? ¿El flujo a través de esa segunda puerta entra o sale de la habitación?

Tendríamos que escribir la ecuación completa para la conservación del flujo másico para encontrar tanto la cantidad como la dirección del flujo a través de la segunda puerta.

(ρ VA) _w ₁ + (ρ VA) _w2 + (ρ VA) _w3 + (ρ VA) _w4 + (ρ VA) _w5 — (ρ VA) _D1 + (ρ VA) _D2 = 0.

Tenga en cuenta que hemos asignado valores positivos al flujo a través de todas las ventanas ya que nos dijeron que el flujo entraba en todas ellas. También hemos asignado un valor negativo al flujo que sale de la primera puerta ya que se decía que el flujo estaba fuera de esa puerta. También tenga en cuenta que no asignamos un letrero (dirección) al flujo a través de la segunda puerta porque no tenemos idea de hacia dónde va. Ahora bien, si ponemos toda la información necesaria para las cinco ventanas y la primera puerta en los términos de la ecuación y si conocemos el área de la segunda puerta y asumimos que la densidad es la misma en todas partes (flujo incompresible), podemos resolver por la velocidad (velocidad) del flujo usando la relación de conservación de masa arriba y encontrar tanto la magnitud de la velocidad como su dirección (signo).

Ejercicio 2.1

Intente hacer el problema anterior asumiendo que las cinco ventanas son de 2 pies X 4 pies de tamaño y que el aire está soplando a 20 pies/seg.

Supongamos que las dos puertas tienen un tamaño de 3 pies X 7 pies y que el flujo de salida de la primera puerta se mide a 50 pies/seg.

Encuentra la velocidad y dirección del flujo a través de la segunda puerta.

NOTA: Aquí consideramos todo el flujo hacia nuestro “sistema” o “volumen de control” como POSITIVO, y todo el flujo FUERA del sistema como NEGATIVO. Si no conocemos su dirección, asumimos que es positivo en valor y la solución de la ecuación nos dará una respuesta negativa si asumimos la dirección equivocada. Posteriormente, cuando observemos la Ecuación de Momentum usaremos un vector unitario, n, para asignar una dirección positiva dentro de nuestro sistema de ejes elegido para el flujo a través de una abertura, y ese vector unitario siempre apuntará FUERA del sistema.

Bien, eso fue bastante simple, pero ¿cómo lidiamos con la conservación masiva cuando estamos mirando el flujo a través de un motor a reacción o una hélice?

La conservación de masa a través de una hélice o un motor a reacción funciona igual que la conservación de masa en un flujo que atraviesa una habitación. De hecho, para el motor a reacción es incluso más sencillo que el cuarto promedio porque solo hay una entrada y salida bien definidas, ¿o es ese realmente el caso?

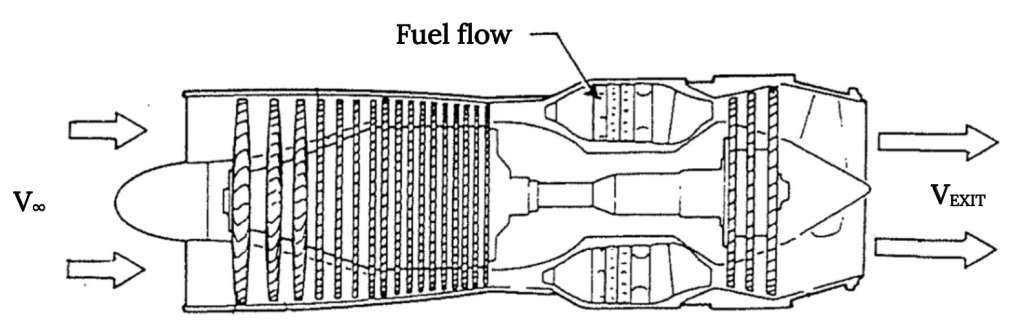
Una sección transversal de un motor turborreactor muestra que el flujo de aire que entra a velocidad cpa V sub infinito primero debe pasar a través de varios juegos de aspas del compresor ya que se comprime en áreas cada vez más pequeñas. Luego se envía más allá de la cámara de combustión donde el flujo de combustible controla la tasa de combustible que se agrega para la combustión. El aire luego se expande a través de un conjunto de álabes de turbina, saliendo de la boquilla de salida a la velocidad de la tapa V sub salida — Figura 2.4: Flujos másicos para un Motor Turbo-Jet

Técnicamente, hay una segunda fuente de masa entrante en cualquier motor a reacción y ese es el flujo másico de combustible que ingresa al motor. Hay aire entrando en la entrada del motor de un área conocida a (supuestamente) una velocidad y densidad conocidas, pero el flujo que sale del motor no es realmente solo aire, es el gas que proviene de la combustión del aire entrante y el combustible entrante. El caudal másico que sale de la salida debe dar cuenta tanto de la masa del aire entrante como del combustible entrante, por lo que nuestra relación de conservación masiva debe reconocerlo.

(dm/ dt) _entrada + (dm/dt) _combustible + (dm/dt) _escape = 0

Normalmente escribiríamos esto como:

(ρ AV) _entrada + (dm/dt) _combustible = — (ρ AV) _escape.

Entonces debemos conocer el caudal másico del combustible. Por lo general, el caudal másico del combustible es muy pequeño en comparación con el del aire de entrada por lo que quizás ese término se pueda descuidar. Entonces, ¿cuál es el problema? Si podemos descuidar el caudal de combustible estamos de vuelta a la ventana, un ejemplo de puerta y la vida es fácil. Desafortunadamente hay otro factor que no debemos olvidar y ese es la densidad. Por lo general, el flujo a través del escape de un motor a reacción va bastante rápido, cercano o mayor que la velocidad del sonido; es decir, ya no podemos asumir que la densidad es constante como lo hicimos en el ejemplo de ventilación de la habitación.

Para resolver este problema tenemos que conocer ya sea la densidad de flujo de salida o su velocidad para resolver la ecuación para el “otro” parámetro (velocidad de salida de densidad), y dado que el flujo másico del combustible contribuye a esta densidad de salida probablemente no deberíamos asumir que es despreciable aunque su velocidad sea casi despreciable.

Hacer aún más compleja la conservación de masa para un jet es el hecho de que la mayoría de los jets actuales son “chorros de ventilador” donde hay esencialmente dos flujos de entrada, uno que atraviesa el núcleo del motor, mezclándose con el combustible para formar un escape de alta velocidad, y otro, más grande, flujo que se acelera a través del ventilador. Podríamos analizar este problema teniendo en cuenta dos flujos de entrada separados y dos flujos de salida separados, o asumiendo (correctamente en la mayoría de los casos) que los dos flujos de salida se mezclan antes de dejar la cubierta del motor o “góndolas” para formar un escape único y mixto.

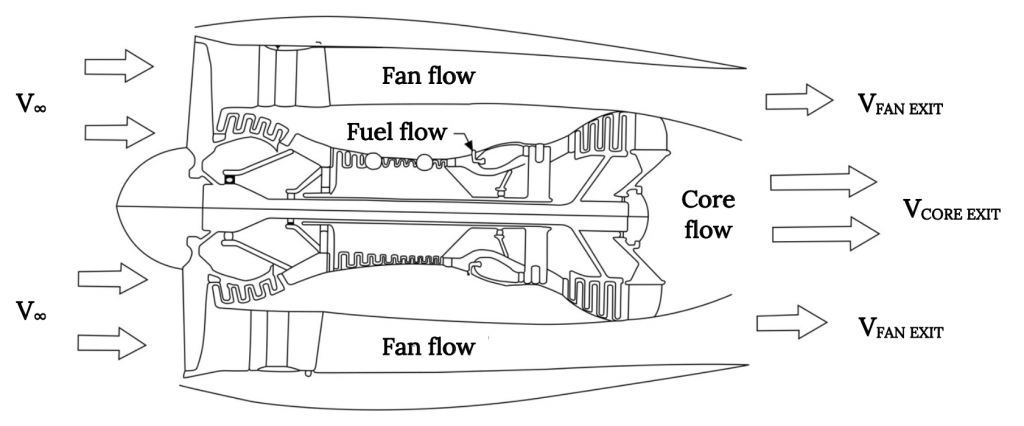
Una sección transversal de un motor a chorro de ventilador muestra que el aire que entra en la tapa de velocidad V sub infinito tiene dos caminos a tomar. Los bordes exteriores pasan por el ventilador y continúan sin interrupciones fuera de la parte posterior del motor a la salida del ventilador secundario de la tapa de velocidad V. Las porciones centrales se mueven a través de un conjunto de ventiladores del compresor hacia una cámara de combustión donde el flujo de combustible determina cuánto se agrega para la combustión. Luego, el aire pasa a través de los ventiladores de la turbina y sale como el flujo central, con la salida del subnúcleo de la tapa de velocidad V. — Figura 2.5: Flujos a través de un Motor a Chorro de ventilador

En cualquier caso, el problema del flujo del motor a reacción es un poco más sencillo de entender para muchas personas que el problema del flujo de la hélice porque las áreas de entrada y salida normalmente están bastante bien definidas. ¿Cómo definimos los flujos de entrada y salida cuando dibujamos el flujo a través de una hélice?

Cuando un flujo está pasando por una hélice, ¿cuáles son las áreas de entrada y salida? Realmente no hay entrada ni salida física. Por supuesto, sabemos que el flujo pasa por la propia hélice, entonces, ¿se usa el área de hélice tanto para la “entrada” del flujo como para su “salida”? Esto apenas tiene sentido. ¿Cómo podemos hablar de los cambios en el flujo entre la entrada y la salida cuando no hay distancia física entre la entrada y la salida?

Veamos lo que sabemos intuitivamente sobre el flujo a través de una hélice (o un ventilador). Sabemos que el flujo detrás de la hélice o ventilador se mueve más rápido que el flujo frente a él. Sabemos que de alguna manera, una manera que se puede analizar en detalle al mirar cada hélice o aspa de ventilador como una pequeña ala giratoria que sí funciona en el aire, la hélice esencialmente agrega energía al flujo. También sabemos, si lo pensamos un poco, que no podemos usar la ecuación de Bernoulli para comparar el flujo aguas arriba y aguas abajo del puntal o ventilador porque la energía se agrega en el puntal o ventilador y la ecuación de Bernoulli asume que la energía es constante a través del flujo. También sabemos que hay límites a lo que un ventilador o hélice puede hacer para acelerar un flujo debido a los límites de velocidad de punta en las propias palas y estos límites esencialmente significan que podemos asumir de manera bastante segura un flujo incompresible a través del sistema.

Al juntar todos estos hechos, podemos dibujar un cuadro que parece algo así como el flujo debería aparecer a través de una hélice o ventilador. Sabemos que en algún lugar aguas arriba de la hélice el flujo no se altera; es decir, está en condiciones de “corriente libre” o atmosféricas. Sabemos que en algún lugar aguas abajo del puntal la presión estática en la masa de aire que pasó por la hélice debe regresar a su valor de flujo libre.

Imaginaremos un “tubo de corriente”, o trayectoria tridimensional de flujo másico constante, que comienza en el flujo no perturbado aguas arriba del puntal, pasa por el puntal (convirtiéndose en el mismo diámetro que el puntal en esa ubicación, y luego continúa aguas abajo hasta el punto que mencionamos anteriormente donde la presión estática ha vuelto al valor atmosférico. ¿Cómo debe ser ese “tubo de corriente”?

Un tubo de corriente se define como una trayectoria de flujo tridimensional en la que el caudal másico es el mismo en cada punto de su recorrido. Esencialmente, como se muestra en la siguiente figura, el área de sección transversal aguas arriba del tubo de corriente (su área de “captura”) debe tener la misma cantidad de caudal másico a través de él que pasa por el propio puntal. De igual manera, el área de “salida” para nuestro tubo de corriente también debe permitir el paso del mismo flujo másico que pasó por el área de captura y el área de “disco” de apoyo.

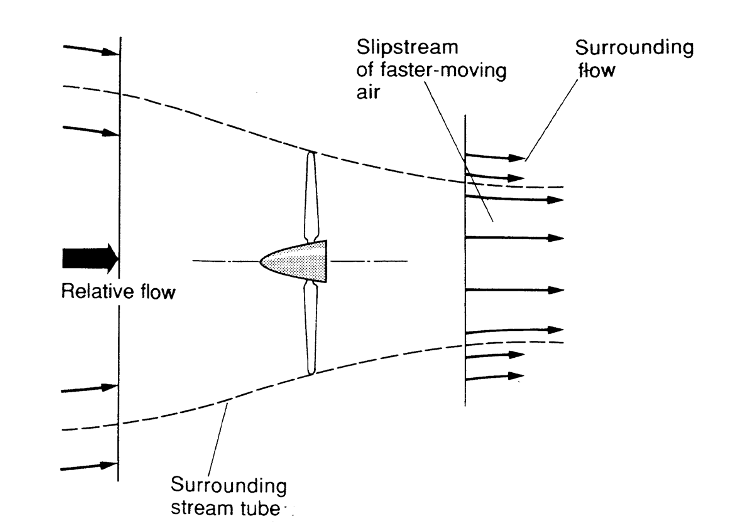
A medida que el flujo relativo se acerca a la hélice, los tubos de corriente se estrechan para coincidir con el ancho de la hélice, luego continúan estrechándose después de pasarla. Esta área estrechada da como resultado una corriente de aire que se mueve más rápido dentro del tubo de corriente, mientras que el flujo circundante es más lento. — Figura 2.6: El concepto de tubo de corriente para un flujo de hélice

Entonces, ¿por qué el “tubo de corriente” en la figura anterior se vuelve progresivamente más pequeño a medida que el flujo va desde la presión atmosférica, el área de captura de corriente libre hasta el área de salida de presión atmosférica en algún lugar aguas abajo? Primero, sabemos que la velocidad en el área de salida debe ser mayor que en el área de captura (entrada); por lo tanto, si el caudal másico es el mismo y el flujo es incompresible, el área debe disminuir en proporción inversa a los aumentos de velocidad. Pero, ¿por qué asumimos que esta disminución de área (y aumento de velocidad) es suave y continua? ¿No hay simplemente un gran salto de velocidad a través del disco propulsor?

Bueno, probablemente podríamos analizar todo en términos de algún tipo de salto instantáneo en la velocidad de flujo en el disco propulsor basado en un balance energético, asumiendo que la energía agregada por el puntal produce un aumento repentino en la energía cinética de flujo y velocidad. Sin embargo, sabemos por las mediciones del mundo real que este aumento de velocidad no es instantáneo y que parte del aumento se ve frente a la hélice a medida que el flujo se acelera desde su velocidad de “corriente libre” a la velocidad justo en la parte delantera del disco de hélice. También sabemos que toma un par de diámetros de hélice aguas abajo antes de que el flujo en el “propwash” alcance la velocidad máxima. En base a esta combinación de realidad y conveniencia, elegimos modelar el aumento de velocidad como uno continuo dentro de un “tubo de flujo” con forma de boquilla convergente de sección transversal circular, como se muestra en la figura anterior.

Esta imagen ideal, por supuesto, ignora muchas cosas como las pérdidas por turbulencia y efectos de flujo rotacional; sin embargo, es uno que funciona bastante bien. Entonces, ¿qué proponemos hacer con este modelo y con el modelo del flujo a través de un motor a reacción? Lo que queremos hacer es usarlos para determinar cómo se produce el empuje y encontrar las propiedades que determinan cómo varía el empuje con la velocidad y la altitud.

2.4.2 Empuje

Nuestro objetivo es echar un vistazo a la propulsión. ¿Cómo contabilizamos el empuje o la potencia en las evaluaciones de desempeño de las aeronaves?

Hay dos formas de hacerlo. Uno miraría las adiciones de energía al flujo y una conservación de energía. Pero, como se señaló en la discusión de la hélice anterior, esto sería muy tedioso, requiriendo que hagamos análisis aerodinámicos de cada pala de hélice, teniendo en cuenta las pérdidas debidas a los efectos de compresibilidad cerca de las puntas de las palas y por la interferencia entre el flujo sobre una pala y la siguiente pala. Hay libros sobre cómo hacer esto, el más antiguo de los cuales pasó bajo títulos como “Airscrew Theory”, y este es el tipo de análisis que deben utilizar las empresas que fabrican hélices. El problema sería aún más interesante en un motor a reacción con nosotros teniendo que dar cuenta de las ganancias y pérdidas de energía debido al flujo alrededor de las palas del compresor y las palas de turbina, la combustión del combustible y el flujo a través de las boquillas internas.

Resulta que la forma más sencilla de ver el empuje es mirar la conservación del impulso.

2.4.3 Conservación del impulso

La conservación del impulso, como la conservación masiva y la conservación de energía, es una de las “tres grandes” “leyes” de conservación que todos vimos en algún curso de Física. De cara a ello, la conservación del impulso es un concepto sencillo. Así como en la conservación masiva de un flujo debemos dar cuenta de todos los flujos de masa que entran o salen del campo de flujo en consideración, al mirar la conservación del impulso debemos considerar todas las cosas que posiblemente podrían dar cuenta de los cambios de impulso y, en última instancia, en las fuerzas.

Esencialmente, el concepto que estamos viendo es aquel que dice que el cambio de impulso en un cuerpo o “sistema” con el tiempo debe igualar las fuerzas sobre ese cuerpo o sistema. La idea es que o bien las fuerzas sobre un cuerpo o sistema harán que su impulso cambie o un cambio de impulso dentro del sistema o cuerpo dará como resultado una fuerza.

(d/dt) (impulso) = (d /dt) (mv) = Fuerza

Esta es una idea simple que a menudo se hace para parecer muy complicada cuando se deriva en la mayoría de los libros de texto sobre mecánica de fluidos. Si, por ejemplo, pateas un balón de fútbol, la fuerza que impartas al balón resultará en un cambio de impulso en el balón. Si el balón estaba parado antes de que fuera pateado, la fuerza cambiará su impulso de cero a un valor relacionado con la fuerza del impacto y la masa del balón. Si la pelota ya se estaba moviendo, la patada puede enviar moviéndose en otra dirección, por lo que este concepto es direccional; es decir, es un concepto vectorial, como se esperaría cuando se involucra una fuerza.

Al mirar la propulsión de los aviones nos interesa la acción inversa; es decir, crear un cambio de impulso para obtener una fuerza, cambiando el impulso del flujo a través del motor o hélice para crear empuje.

Así como al trabajar con la ecuación de Bernoulli tuvimos la opción de modelar el flujo como un fluido en movimiento que pasa por un ala o cuerpo, o como un cuerpo que se mueve a través del aire inmóvil, tenemos que hacer una elección similar aquí. Nosotros, por ejemplo, optaremos por mirar el flujo a través de un motor a reacción o una hélice como si el motor (prop) estuviera parado y el flujo se estuviera moviendo más allá de él. Esto es realmente una elección entre tener que considerar el impulso del motor en movimiento o el impulso del aire en movimiento. Cualquiera de las dos vistas dará la misma respuesta para el empuje, pero el modelo de aire móvil suele ser un poco más fácil de trabajar con él. De cualquier manera, debemos tener mucho cuidado para dar cuenta de todos los posibles cambios de impulso tanto en el motor como en el flujo.

Primero tenemos que analizar qué tipos de cambios de impulso podrían estar presentes, así como qué tipo de fuerzas podrían estar involucradas. Para ello, veamos uno de los motores “jet” más simples, pero uno de los más difíciles de analizar, un globo de goma que se infla y se libera.

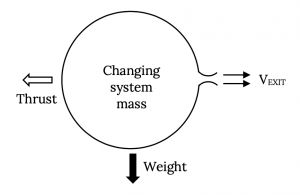
A medida que la masa total del balón cambia debido al aire que sale por el agujero, el gas sale con una salida secundaria V de tapa de velocidad a la derecha, lo que resulta en una fuerza neta de empuje hacia la izquierda. Estos son perpendiculares a la fuerza de peso descendente del globo. — Figura 2.7: Un globo como un chorro simple

Veamos la ilustración anterior y enumeremos todas las formas en que el impulso podría desempeñar un papel, así como todas las fuerzas involucradas. Habrá al menos dos fuentes de cambio de impulso para el globo y al menos tres fuerzas que podrían estar involucradas.

Fuentes de cambio de impulso:

El cambio en el momento del globo (el “sistema”) con el tiempo debido al cambio en la masa de aire dentro del globo con el tiempo y debido a cualquier cambio en la velocidad de esa masa. [A medida que el globo expulsa aire a través de su entrada/salida, la masa del “sistema” mismo está cambiando y, aunque su velocidad fuera constante, el impulso del sistema cambiaría.]
El momento del flujo que sale del “sistema” (globo); es decir, el flujo másico de aire a través de la entrada/salida (chorro) multiplicado por su velocidad.

Ambos términos anteriores son direccionales debido a las velocidades asociadas con ellos. El momento del globo en sí está relacionado con la velocidad del globo y el momento del flujo a través de la salida obviamente está relacionado con la dirección del flujo a través de la salida.

Fuerzas en el globo:

La mayor fuerza sobre el globo será la que elijamos llamar empuje. Esto es esencialmente lo que estamos tratando de encontrar.
otra fuerza sobre el globo que tal vez no pensemos al principio es la debida a la gravedad; es decir, su peso.
Por último, habría fuerzas de presión provocadas por presiones que actúan sobre las zonas. Estos pueden incluir arrastre de presión sobre el globo mismo o diferencias en la presión a través de los límites del sistema. A menudo encontramos que las fuerzas de presión tienden a equilibrarse o a sumar a cero pero hay algunos casos en los que éstas deben ser consideradas.
También podríamos considerar fuerzas de fricción o incluso fuerzas electromagnéticas u otras si así lo deseáramos pero nos limitaremos a las tres primeras fuerzas mencionadas anteriormente.

¿Cómo describimos cada una de estas fuentes de cambio de impulso o fuerzas de una manera muy general? Echemos un vistazo a cada uno de estos enumerados anteriormente.

1. El cambio en el momento del “sistema” con el tiempo implica los cambios tanto en la masa como en la velocidad del sistema:

d/dt [(masa) (velocidad)],

y, dado que la masa del sistema puede escribirse como su densidad multiplicada por su volumen, podríamos ver esto como

d/dt [(densidad) (volumen) (velocidad)]

2. El cambio en el momento debido al flujo de salida (y en general) al sistema con el tiempo es esencialmente el caudal másico (dm/dt) a través de cualquier entrada o salida multiplicado por la velocidad a la que esa masa está pasando por las áreas de entrada o salida. Sabemos que el caudal másico es la densidad multiplicada tanto por la velocidad como por el área de sección transversal del flujo, por lo que este término se expresa como:

(dm/dt) (velocidad) = (densidad) (velocidad) (área) x (velocidad).

3. El peso es solo la masa (densidad x volumen) multiplicada por la aceleración de la gravedad.

(densidad) (volumen) (g).

4. Las fuerzas de presión son solo presiones que actúan sobre un área:

(presión) (área)

Ahora bien, para trabajar con todos estos necesitamos ponerlos juntos en forma de algún tipo de ecuación. La ecuación debe decir esencialmente que los cambios de impulso deben ser equilibrados por las fuerzas involucradas. Esto puede pensarse como fuerzas que provocan un cambio de impulso (el pie del futbolista patea la pelota) o cambios de impulso que provocan fuerzas (el empuje de un globo liberado). La ecuación que suele resultar de una derivación mucho más formal es una relación vectorial de aspecto complicado llamada ecuación de impulso.

2.4.4 La Ecuación del Momentum

$ddtrρv¯dr+sρv¯ (v¯n^) dsCambio de impulso en fluido=−fe−sρn^ds+rρg¯drFuerzas que causan cambio de impulso$

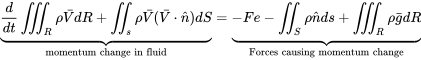
Antes de entrar en pánico ante la notación vectorial y las integrales dobles y triples, respira hondo y ve cómo estos términos se relacionan con los presentados anteriormente.

Una triple integral sobre “R” (la “región” matemática o el “sistema”) no es más que el volumen. Si la densidad y velocidad de todo lo contenido en la región o sistema es la misma; es decir, si es un sistema homogéneo, entonces este término no es más que la derivada temporal de la densidad multiplicada por el volumen por la velocidad; es decir, de la masa del sistema por su velocidad como se indicó en la sección arriba.

Entonces, ¿por qué lo hacemos tan complicado mirar? Una razón podría ser solo para impresionar a nuestros amigos en las artes liberales o para mostrarles a nuestros padres lo duros que son nuestros cursos. Una mejor razón es permitir que la ecuación de momentum tenga en cuenta los efectos del sistema no homogéneos. Supongamos, por ejemplo, que nuestro “sistema” no era un globo lleno de agradable aire homogéneo, sino una pelota de béisbol o pelota de golf con un relleno sólido hecho de varias capas, cada una con diferentes densidades, y además, que alguien hubiera hecho la pelota con su núcleo más pesado algo “descentrada”. Puedes comprar tales pelotas de golf “trick” en tiendas de novedades y cuando las golpeas con un palo de golf (¡imparte fuerza al sistema!) , en lugar de viajar en línea recta se tambalean como si estuvieran borrachos. Debido a que la ecuación de impulso puede explicar esta “no homogeneidad”, puede explicar el movimiento tambaleante de la pelota de golf truco. De manera similar el último término a la derecha, el término gravedad o peso, puede explicar los efectos gravitacionales sobre una masa no homogénea.

Dos de los términos de la ecuación tienen dobles integrales. Ya podrías haber adivinado que la doble integral sobre una distancia “S” debe relacionarse con algún tipo de área, y mirar los términos lo confirmaría. El término integral doble a la izquierda se refiere al impulso llevado con un flujo dentro o fuera del sistema sobre una zona de entrada o salida. Este término se escribe de esta manera compleja para poder dar cuenta de velocidades no uniformes sobre la entrada o salida e incluso densidades no uniformes sobre estas áreas. Si asumimos que todo el flujo de entrada o salida es el mismo fluido que se mueve a la misma velocidad entonces los términos de densidad y velocidad pueden salir de la integral y la integral misma se convierte en nada más que el área de entrada o salida. Entonces, de nuevo, ¿por qué hacer que se vea así de complicado? Bueno, en muchos casos el flujo que sale de una abertura no es uniforme porque las fuerzas de fricción hacen que se mueva más lentamente cerca de los bordes de la abertura que en el centro, y esta forma integral de la ecuación de impulso puede explicar eso si queremos que así lo haga. De manera similar, el término de presión en el lado derecho de la ecuación puede explicar la variación de presión sobre una superficie.

¿Qué pasa con la notación vectorial, el término V • n, en el término integral doble de la izquierda? Primero, la ecuación de momentum es una ecuación vectorial, lo que significa que cada uno de los términos tiene una dirección y la solución de la ecuación para una fuerza como empuje o arrastre dará tanto una magnitud como una dirección para esa fuerza. Segundo, para uno de los términos en cada lado de la ecuación, es solo el parámetro “normal” a una superficie o límite definido el que provocará una fuerza y el “vector unitario” n se usa para designar esa dirección normal. Siempre definiremos la dirección para este vector unitario como señalar fuera del sistema, incluso donde el flujo está entrando en el sistema.

¿Qué significan entonces estas cantidades vectoriales? Cada una de las velocidades puede tener hasta tres términos en ellas, uno asociado a cada dirección en un sistema de ejes seleccionado. En el caso de velocidad en un sistema convencional de ejes x, y, z, normalmente usamos los términos u, v y w para designar los componentes x, y y z de la velocidad, respectivamente. Entonces escribiríamos un vector de velocidad como:

V = u i + v j + w k,

donde i, j y k son los vectores unitarios en las direcciones x, y y z positivas. De manera similar, el vector de gravedad podría tener hasta tres componentes; sin embargo, a veces tratamos de definir nuestro sistema de coordenadas de manera que un eje esté en la dirección de la aceleración gravitacional para eliminar dos de estos componentes.

El término V • n es entonces el “producto punto” de dos vectores donde tanto los vectores V como los n pueden tener componentes x, y y z, pero solo los componentes dirigidos similares se multiplican entre sí, luego suman para dar una cantidad “escalar” con una magnitud pero sin dirección. Entonces, si la velocidad está en la misma dirección que el vector normal (como suele ser el caso de los flujos que entran o salen de un sistema) el resultado es simplemente la magnitud de la velocidad. En el otro extremo, si la velocidad está en un ángulo de 90 grados con respecto al vector normal, el producto de punto da cero.

De nuevo uno podría preguntarse, ¿por qué complicar tanto las cosas con todas estas integrales y vectores y productos dot y similares? Se hace de esta manera porque es una ecuación muy versátil que puede dar cuenta de un movimiento totalmente tridimensional. Por ejemplo, si ese futbolista pateara la pelota en un ángulo de 90 grados con respecto a su dirección de movimiento existente, esta relación, siempre y cuando conociéramos la fuerza de la patada y la masa y velocidad de la pelota, nos diría la nueva dirección y velocidad de la pelota a pesar de que la dirección no estaría ni en la dirección original del movimiento o en la dirección de la patada. De igual manera, si hay una curva en una tubería podemos usar la ecuación para encontrar la magnitud y dirección de la fuerza que ocurrirá cuando el agua fluya a través de esa curva en la tubería.

El truco para usar la ecuación de impulso es seguir la regla general que a menudo distingue a un ingeniero de un científico o matemático puro; es decir, usar la alineación adecuada de los sistemas de ejes y establecer límites del sistema y hacer buenas suposiciones que eliminen la mayor parte de la complejidad posible. Afortunadamente podemos hacer mucho de esto ya que usamos la ecuación de impulso para mirar el empuje.

2.4.5 Empuje (de nuevo)

Veamos el flujo a través de un motor a reacción en términos de la ecuación de impulso.

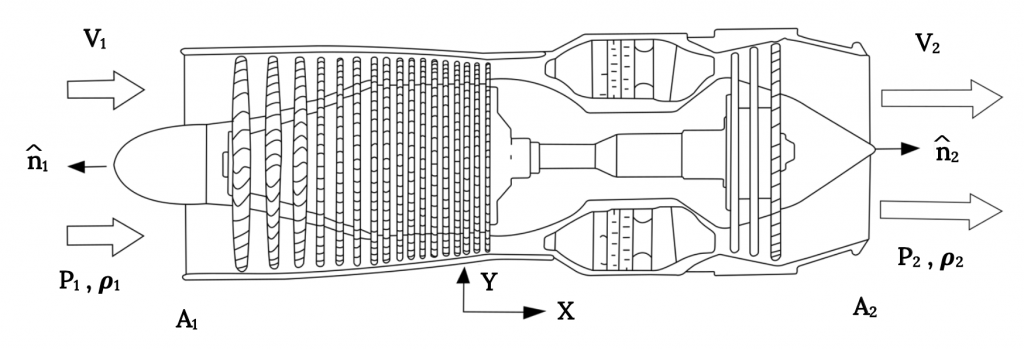
En la admisión para el motor turborreactor con un área de tapa A sub 1, la normal apunta hacia afuera, hacia la izquierda, mientras que el aire que fluye hacia el motor a velocidad cap V sub 1, tapa de presión P sub 1, y densidad rho sub 1, entran a la derecha. En la salida con una tapa de área A sub 2, la normal apunta hacia afuera, hacia la derecha, alineada con el flujo de aire de salida a velocidad cap V sub 2, tapa de presión P sub 2, y densidad rho sub 2. — Figura 2.8:Términos de la ecuación de Momentum para Turbo-Jet

En la ilustración anterior hemos alineado el motor con el eje “x” y tenemos flujo que entra en la entrada del motor en la dirección x y otro flujo que sale del motor, también en la dirección x. Queremos conocer el empuje en función de esta información. Veamos qué podemos decir sobre los diversos términos en la ecuación de momentum.

El primer término en el lado izquierdo de la ecuación es un término “dependiente del tiempo” para dar cuenta de los cambios en el impulso del “sistema” mismo con el tiempo. Aquí nuestro sistema es todo el motor a reacción, y, si asumimos que el motor (avión) está en vuelo de velocidad “constante” o constante, no hay nada en el término (densidad, velocidad o volumen) que vaya cambiando con el tiempo. Entonces, este término es cero.

El segundo término a la izquierda explica el impulso llevado dentro o fuera del sistema a medida que el flujo entra o sale. Obviamente, este término no va a desaparecer ya que tenemos aire entrando al motor y los productos de combustión saliendo por el otro extremo. Primero tenemos que preguntar si estos dos flujos son “uniformes” a través de sus respectivas áreas de entrada o salida. Si podemos suponer que son uniformes y podemos suponer que todo el flujo tiene la misma densidad, entonces este término (en realidad dos términos, uno para la entrada y otro para la salida) se convierte en:

ρ ₁ V ₁ (V ₁ •n ₁) A ₁ + ρ ₂ V ₂ (V ₂ •n ₂) A ₂.

Ahora bien, ¿qué hacemos con el negocio del vector? Los flujos están ambos en la dirección x positiva. El primer vector unitario normal está en la dirección x negativa mientras que el segundo está en la dirección x positiva. El resultado es:

— ρ ₁ V ₁ ² A ₁ + ρ ₂ V ₂ ² A ₂, (todo en la dirección x)

Ok, eso cuida el lado izquierdo de la ecuación de momentum. ¿Qué pasa con los términos de la derecha? El primer término a la derecha es la fuerza “externa” que, en este caso, es el empuje que queremos encontrar. El segundo término a la derecha es quizás el más difícil de entender físicamente por lo que volveremos a esto.

El tercer término a la derecha es el término de gravedad, realmente el peso. Si asumimos que esto está actuando en un ángulo de 90 grados con respecto al eje x o a la dirección de vuelo y así es perpendicular a todas las demás fuerzas y cambios de impulso en los que tenemos interés podríamos simplemente descuidar este término. En realidad sería más apropiado decir que su componente en la dirección x es cero. En realidad, este término nos diría que debe haber una fuerza para oponerse al peso y esta sería la elevación aerodinámica que, a su vez, estaría relacionada en la ecuación de momentum con un cambio vertical en el impulso del flujo a medida que se desplazaba alrededor del ala y la distribución de presión correspondiente alrededor el ala. En esencia estamos optando por ignorar los componentes verticales de las fuerzas y los cambios de impulso.

Ahora volvamos al segundo mandato por la derecha, el único término con presiones en él. Este término analiza las fuerzas provocadas por las presiones que actúan sobre las zonas. Si estuviéramos viendo la fuerza de sustentación usaríamos este término para integrar la distribución de presión alrededor de un ala. En el motor asumiremos que los flujos sobre el exterior de la carcasa o góndolas del motor son simétricos, es decir, que existe la misma distribución de presión en la parte superior que en la parte inferior de la góndula, y que el efecto neto de estas presiones (al menos en la dirección x) es cero. Pero ¿qué pasa con las presiones a través de la entrada y salida?

Presiones a través de la entrada y salida?!! ¿Cómo puede significar esto algo cuando aquí no hay superficies reales, solo flujos entrando o saliendo? Aquí es donde se pone interesante el concepto de un límite de “sistema”. Cuando hay un límite real como la góndula del motor, los límites del sistema son fáciles de entender. Pero estos extremos “abiertos” del “sistema” son también límites sobre los cuales debemos dar cuenta de todos los términos de la ecuación. En otras palabras, así como tuvimos que dar cuenta del flujo a través de estos límites un tanto imaginarios, también debemos dar cuenta de los cambios de presión a través de ellos. Pero, ¿cómo pueden estas presiones causar fuerzas reales cuando no hay superficies “reales” sobre las que puedan actuar? Esto se convierte en uno de esos “saltos de fe” que muchas veces debemos tomar al aplicar ecuaciones a situaciones físicas.

No, no hay superficies en la entrada y salida donde las diferencias de presión a través de la superficie provoquen una fuerza; sin embargo, debemos contabilizarlas de todos modos si existe un diferencial de presión entre la atmósfera circundante y el flujo hacia la entrada y salida. Este es probablemente el más fácil de entender cuando miramos el flujo de escape.

Al salir del escape hay un flujo de los productos de combustión de aire y combustible que ha sido calentado y presurizado en la cámara de combustión del motor. Después de la combustión queremos convertir esa energía agregada en un impulso lo más alto posible (el segundo término en el lado izquierdo de la ecuación de impulso). Esto significa que queremos “expandir” el gas en una boquilla de salida, bajando su presión con un incremento correspondiente de velocidad (ecuación de ala Bernoulli) tanto como sea posible para obtener un impulso alto. La situación ideal es expandirla hasta el punto en que el gas que sale tenga la misma presión que la atmósfera a la que saldrá. Si se expande demasiado o muy poco habrá pérdidas ya que la presión del flujo llega a equilibrio con la atmósfera. Resulta (y la ecuación de impulso esencialmente nos dice esto) que las pérdidas por sobreexpansión o subexpansión son equivalentes a la fuerza de presión que estaría en una superficie con la misma área que la salida con una diferencia de presión igual a la baja o sobreexpansión delta-P. Es por ello que algunos chorros de alto rendimiento tienen boquillas de salida de área variable en sus motores.

El mismo problema puede ocurrir en menor grado en la entrada del motor, pero una entrada del motor y una sección del compresor adecuadamente diseñadas pueden eliminar la mayor parte de la pérdida.

Entonces, ¿cómo lidiamos con este término de presión? O bien debemos conocer las diferencias entre la presión atmosférica y las de los flujos de entrada y salida y computar valores para estos términos, teniendo cuidado de dar cuenta adecuadamente de los signos del vector unitario, o debemos asumir que estas pérdidas son insignificantes. Tomemos la salida fácil y supongamos que estos términos son de poca importancia porque tenemos un motor debidamente diseñado.

Bien, ¿dónde nos deja esto? Hemos terminado con una ecuación relativamente simple:

— ρ ₁ V ₁ ² A ₁ + ρ ₂ V ₂ 2 A ₂ = — Fe

reorganizar esto da:

Empuje = Fe = ρ ₁ V ₁ ² A ₁ — ρ ₂ V 2 ² A ₂.

Al mirar esto vemos que el segundo término a la derecha será mucho mayor que el primer término, por lo que, el empuje tendrá un signo negativo. ¿Esto está bien? Seguro que lo es. Simplemente dice que la fuerza de empuje está en la dirección x negativa, hacia la izquierda, tal como queremos que sea.

¡Guau! Eso seguro fue mucho trabajo para obtener una respuesta bastante obvia ; ¡el empuje es igual al cambio de impulso de la entrada del motor a la salida! ¿No es esto algo intuitivo? Sí, es algo intuitivo para muchos de nosotros. Por otro lado sí mantiene felices a los matemáticos y teóricos entre nosotros, y lo que es más importante, nos dice que al llegar a esta respuesta “intuitiva” hemos hecho algunas suposiciones importantes sobre la presión comportamiento y selección del sistema de ejes, etc.

Ok, ahora que tenemos todo eso en nuestro haber ¿qué datos importantes sobre la propulsión pueden extraerse de esta solución? Para ver esto, juguemos un poco con la ecuación anterior al dar cuenta de la conservación de la masa.

Ahora bien, reconociendo que V ₁ es nuestra velocidad de “flujo libre”, V _∞, y que la densidad del aire entrante es también la de la atmósfera, ρ _∞, podemos escribir esto como

Empuje = ρ _∞ V _∞ ² A ₁ — ρ ₂ V 2 ² A ₂

Y mirando sólo a la magnitud del empuje (como se dijo anteriormente, la relación anterior da un empuje negativo, significando simplemente que está a la izquierda en nuestra ilustración original del motor moviéndose de derecha a izquierda)

Empuje = ρ ₂ V ₂ ² A ₂ — ρ _∞ V ∞ ² A ₁

Ahora definimos el “empuje estático” como T ₀, el empuje cuando el motor está parado (V _∞ = 0). Esta es la cantidad de empuje que se mediría en un banco de pruebas de motor y es una pieza estándar de información que existiría para cualquier motor.

T ₀ = ρ ₂ V ₂ ² A ₂

Esto nos permite reescribir la relación general de empuje como:

Empuje = T ₀— ρ _∞ V _∞ ² A ₁,

o simplemente como:

T = T ₀ — a V _∞ ²,

donde:

a = ρ _∞ A ₁

¿Qué nos dice todo esto? Primero, todas las ecuaciones de empuje nos dicen que el empuje es una función de la densidad atmosférica. A diferencia de la velocidad, que antes encontramos que variaba con la raíz cuadrada de densidad, el empuje disminuye en proporción directa a la disminución de la densidad en la atmósfera. Así, escribimos:

T _alt = T _sl (ρ _alt/ρ _SL)

Esta es una relación importante entre el empuje y la altitud que utilizaremos en todos los cálculos de rendimiento.

Segundo, aprendemos que, en general, el empuje de un motor varía con la velocidad según la relación:

T = T ₀ — a V _∞ ²

Cabe señalar, como siempre, que estas ecuaciones implican suposiciones importantes, como la suposición de que la presión de salida del motor y la presión de entrada son ambas iguales a la presión en la atmósfera de corriente libre. Los pilotos de aviones a reacción le dirán que la relación de empuje a empuje estático que se muestra arriba no da cuenta, por ejemplo, de una sobretensión del motor en la aceleración inicial por la pista ya que se produce un “efecto de ariete” en la entrada del motor. Este “efecto carnero” es esencialmente uno de estos efectos de presión que elegimos ignorar.

2.4.6 Empuje de hélice

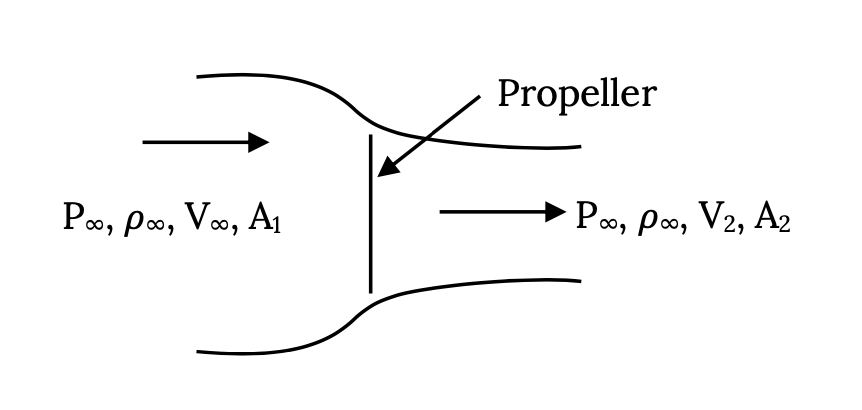
Cabe señalar que obtendríamos esencialmente exactamente la misma ecuación de empuje mirando el flujo a través de una hélice como lo hacemos con un motor a reacción. Teniendo en cuenta una discusión anterior, dibujaríamos nuestro “sistema” como se muestra a continuación usando límites que representan un “tubo de corriente” de flujo másico constante. En este caso no tenemos una manera fácil de conocer los valores exactos para el área de flujo de entrada o el área de salida pero obtendríamos exactamente la misma ecuación que encontramos para el jet y aún encontraríamos

T = T ₀ — a V _∞ ².

El flujo de aire se acerca a una hélice con tapa de presión P sub infinito, densidad rho sub infinito, tapa de velocidad V sub infinito y tapa de área A sub 1. El aire entonces sale más allá de la hélice con la misma presión y densidad, pero una velocidad actualizada de cap V sub 2 y área reducida cap A sub 2. La tapa de empuje T todavía se muestra igual al nudo T de la tapa de empuje estática menos la velocidad del sonido a veces la tapa V sub infinito al cuadrado. — Figura 2.9:Términos de la ecuación de impulso para el flujo de hélice

En este capítulo hemos analizado los modelos relativamente simples de propulsión de aeronaves que utilizaremos para examinar el rendimiento de las aeronaves. Al hacer esto hemos utilizado algunos conceptos físicos básicos de conservación (masa e impulso), los cuales pueden proporcionar herramientas muy poderosas para evaluar fuerzas y movimientos en flujos de fluidos y otras áreas. Hicimos muchas suposiciones simplificadoras a lo largo del camino para entender algunos conceptos muy básicos relacionados con la propulsión a chorro y hélice; en particular, para dar una base para modelar la forma en que tanto el empuje como la potencia varían con la velocidad y la altitud. Estos conceptos los encontraremos muy útiles en capítulos posteriores.

Tarea 2

1. En un túnel de viento la velocidad cambia a medida que cambia el área de la sección transversal del túnel. Si la velocidad en una sección de prueba cuadrada de 6′ x 6′ es de 100 mph, ¿cuál fue la velocidad aguas arriba de la sección de prueba donde el túnel mide 20′ x 20′? Utilizar conservación de masa y asumir flujo incompresible. La conservación de la masa requiere que a medida que el flujo se mueve a través de una trayectoria o un conducto el producto de la densidad, velocidad y área de sección transversal debe permanecer constante; es decir, que ρVa = constante.

2. Se está probando un modelo en un túnel de viento a una velocidad de 100 mph.

a) Si el flujo en la sección de prueba se encuentra en condiciones estándar a nivel del mar, ¿cuál es la presión en el punto de estancamiento del modelo?

(b) La velocidad del túnel se mide mediante un tubo pitot-estático conectado a un manómetro de tubo en U. ¿Cuál es la lectura de ese manómetro en pulgadas de agua?

Referencias

Figura 2.1: Claire Colvin (2021). “Ilustración del Motor TurboJet”. CC BY 4.0.

Figura 2.2: Claire Colvin (2021). “Ilustración de un Motor Turbo-Fan o Fan-Jet”. CC BY 4.0.

Figura 2.3: Claire Colvin (2021). “Ilustración del Motor Turbohélice”. CC BY 4.0.

Figura 2.4: Claire Colvin (2021). “Flujos de masa para un motor turb-jet”. CC BY 4.0.

Figura 2.5: Claire Colvin (2021). “Fluye a través de un motor a chorro de ventilador”. CC BY 4.0.

Figura 2.6: James F. Marchman (2004). “El concepto de tubo de corriente para un flujo de hélice”. CC BY 4.0.

Figura 2.7: Gris Kindred (2021). “Un Globo como un Chorro Simple”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/2.1_20210804

Figura 2.8: Claire Colvin (2021). “Términos de Ecuación de Momentum para Turbo-Jet”. CC BY 4.0.

Figura 2.9: Gris Kindred (2021). “Términos de la ecuación de impulso para el flujo de hélice”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/2.9_20210804

<! — pb_fixme —><! — pb_fixme —>

Search

Text Color

Text Size

Margin Size

Font Type