3.6: Flujo de corriente en dos dispositivos terminales de punto cuántico/molécula única

En esta sección presentamos un modelo simplificado para la conducción a través de una molécula. Se basa en el “modelo de juguete” de Datta, et al. \(^{†}\)que a pesar de su relativa simplicidad describe muchas de las características esenciales de las características de corriente-voltaje de una sola molécula.

El sistema contacto/molécula/contacto en equilibrio se muestra en la Figura 3.6.1. En equilibrio,\(\mu_{1}=E_{F}=\mu_{2}\). Dado que hay dos contactos, este es un ejemplo de un dispositivo de dos terminales. De acuerdo con la convención, etiquetaremos el contacto de inyección de electrones, la fuente, y el contacto aceptor de electrones, el drenaje. Modelaremos la molécula por un punto cuántico. Esto es exacto si el centro de la molécula es mucho más conductor que sus conexiones a los contactos.

Figura\(\PageIndex{1}\): Dispositivo de dos terminales con un conductor de punto molecular/cuántico. En equilibrio no hay flujos de corriente y los niveles de Fermi están alineados.

Ahora, cuando aplicamos un potencial entre los contactos de fuente y drenaje desplazamos el nivel Fermi de un contacto con respecto al otro, i.e.

\[ \mu_{D}-\mu_{S} = -qV_{DS} \nonumber \]

Hay dos efectos sobre la molécula:

1. El efecto electrostático: el potencial en la molécula es cambiado por el campo eléctrico establecido entre los contactos. Los niveles de energía dentro de la molécula se mueven rígidamente hacia arriba o hacia abajo en relación con los contactos.
2. El efecto de carga: Fuera de equilibrio, fluirá una corriente y la cantidad de carga en la molécula cambia. Puede aumentar si la corriente fluye a través de la LUMO, o disminuir si la corriente fluye a través del HOMO.

Desafortunadamente, estos efectos están vinculados: mover los niveles de energía molecular con respecto a los niveles de energía de contacto cambia la cantidad de carga suministrada a la molécula por los contactos. Pero la energía de carga asociada con la transferencia de carga a su vez cambia el potencial de la molécula.

Primero consideraremos los efectos estáticos y de carga de forma independiente.

Electrostática: El Modelo de Divisor Capacitivo del Potencial

Nuestro dispositivo de dos terminales puede ser modelado por un punto cuántico vinculado a la fuente y los contactos de drenaje por dos condensadores,\(C_{S}\) y\(C_{D}\), respectivamente. Los valores de estos condensadores dependen de la geometría del dispositivo. Si la molécula está equiespaciada entre los contactos podríamos esperar eso\(C_{S} ~ C_{D}\). Por otro lado, si la molécula está estrechamente unida a la fuente pero lejos del drenaje, podríamos esperar\(C_{S} \gg C_{D}\). (Recordemos que la capacitancia de un condensador de placa paralela simple es inversamente proporcional al espaciamiento entre las placas).

Figura\(\PageIndex{2}\): Dos dispositivos de molécula única y dos terminales acompañados de posibles perfiles de potencial en el conductor molecular. a) contactos simétricos, b) contactos asimétricos. Nos preocupa el voltaje en el centro de la molécula. Esto está determinado por el factor de división de voltaje,\(\eta\). Se puede obtener a partir de un divisor de voltaje construido a partir de capacitores. Adaptado de F. Zahid, M. Paulsson y S. Datta, “Conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).

Estos dos perfiles de potencial se muestran en la Figura 3.6.2. El voltaje se calcula a partir del divisor capacitivo. Así, un voltaje aplicado, V, desplaza los potenciales químicos tanto de los contactos de fuente como de drenaje:\(^{†}\)

\[ E_{F}= -\frac{1/C_{S}}{1/C_{D}+1/C_{S}}qV_{DS}+\mu_{S} \nonumber \]

Es conveniente utilizar como referencia la energía Fermi de la molécula en equilibrio, es decir, si establecemos\(E_{F} = 0\):

\[ \mu_{S}= +\frac{C_{D}}{C_{S}+C_{D}} qV_{DS} \nonumber \]

\( \mu_{D}= -\frac{C_{S}}{C_{S}+C_{D}} qV_{DS}\)

Podemos definir un factor de división de voltaje,\(\eta\). \(^{†}\)Da la fracción del sesgo aplicado que se cae entre la molécula y el contacto fuente, i.e.

\[ \eta=\frac{C_{D}}{C_{S}+C_{D}} \nonumber \]

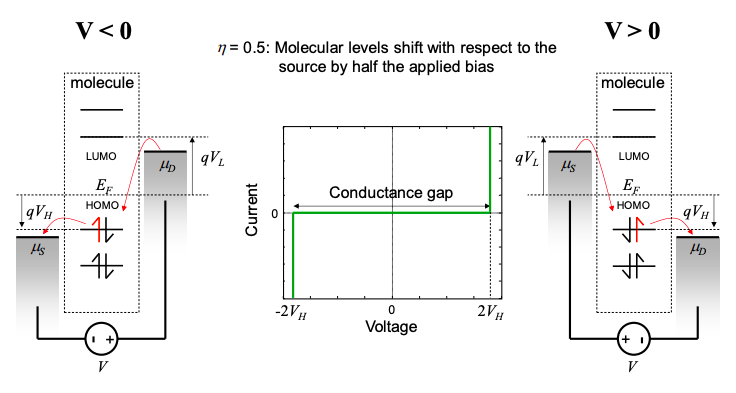
Como se muestra en la Figura 3.6.3, el factor de división de voltaje determina en parte si la conducción ocurre a través del HOMO o del LUMO. Si\(\eta=0\), entonces los niveles de energía molecular se fijan con respecto al contacto de la fuente. A medida que aumenta el potencial del drenaje, la conducción eventualmente ocurre a través del HOMO. Pero si se disminuye el potencial del drenaje, la conducción puede ocurrir a través de la LUMO. La característica de corriente-voltaje de este dispositivo exhibirá un hueco alrededor de la polarización cero que corresponde al hueco HOMO-LUMO. \(^{†}\)

Si\(\eta=0.5\), sin embargo, independientemente de que el sesgo sea positivo o negativo, la corriente siempre fluye a través del nivel de energía molecular más cercano a la energía Fermi. En esta situación, que se cree corresponde a la mayoría de las mediciones de una sola molécula,\(^{1}\) la brecha alrededor del sesgo cero no es la brecha HOMO-LUMO, sino, en este ejemplo, cuatro veces la separación de energía Fermi — HOMO. \(^{§}\)

El factor de división de voltaje es un modelo crudo del perfil de potencial, que de manera más general podría obtenerse a partir de la ecuación de Poisson. \(\eta\)también es probable que varíe con el sesgo. A altos sesgos, puede haber una redistribución de carga significativa dentro de la molécula, lo que lleva a un cambio en\(\eta\). \(^{†}\)

Figura\(\PageIndex{3}\): El factor de división de voltaje es crucial para determinar el nivel de conducción en un dispositivo de molécula única. En este ejemplo, cuando\(\eta = 0\), la conducción siempre ocurre a través del HOMO cuando el sesgo aplicado es positivo, y a través del LUMO cuando el sesgo aplicado es negativo. La brecha de conductancia está determinada por la separación HOMO-LUMO. Adaptado de F. Zahid, M. Paulsson y S. Datta, “Conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).

Figura\(\PageIndex{4}\): Cuándo\(\eta = 0.5\), la conducción siempre ocurre a través del clóset orbital molecular hasta la Energía Fermi. En este ejemplo ese es el HOMO, independientemente de la polaridad del sesgo aplicado. Adaptado de F. Zahid, M. Paulsson y S. Datta, “Conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).

Cargar

Anteriormente, definimos la energía de carga como el cambio en el potencial de la molécula por electrón adicional. Para calcular el efecto neto de la carga necesitamos el número de electrones transferidos.

En equilibrio, el número de electrones en la molécula está determinado por su energía Fermi.

\[ N_{0}=\int^{\infty}_{-\infty} g(E)f(E,E_{F})dE \nonumber \]

Bajo sesgo, la distribución de electrones en la molécula ya no está en equilibrio. Definiremos el número de electrones bajo polarización como N.

Así, el cambio en el potencial en la molécula debido a la carga es

\[ U_{C} = \frac{q^{2}}{C_{ES}}(N-N_{0}) \nonumber \]

Figura\(\PageIndex{5}\): Efecto de la carga sobre una molécula. La adición de electrones desplaza el potencial molecular (y por lo tanto todos los orbitales dentro de la molécula) para repeler la adición de más electrones. Obsérvese que aunque hemos mostrado el cambio esperado en el nivel de Fermi, esto solo es significativo si la molécula permanece en equilibrio. Adaptado de F. Zahid, M. Paulsson y S. Datta, “Conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).

Resumen

El cambio neto en el potencial en la molécula, U, es la suma de los efectos electrostáticos y de carga:

\[ U=U_{ES}+U_{C} \nonumber \]

Al aplicar el voltaje fuente-drenaje relativo a una tierra en la molécula hemos forzado\(U_{ES} = 0\) en la Figura 3.6.4. Pero no siempre será posible ignorar los efectos electrostáticos en U si el suelo se posiciona en otro lugar. Los análisis de transistores, por ejemplo, suelen definir la fuente a conectar a tierra.

Modelamos el efecto del cambio en el potencial cambiando rígidamente todos los niveles de energía dentro de la molécula, i.e.

\[ g \rightarrow g(E-U) \nonumber \]

\(^{†}\)S. Datta, “Transporte cuántico: átomo a transistor” Cambridge University Press (2005). F. Zahid, M. Paulsson, y S. Datta, “La conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).

\(^{†}\)F. Zahid, M. Paulsson, y S. Datta, “Conducción eléctrica en moléculas”. En Semiconductores Avanzados y Nanotécnicas Orgánicas, ed. H. Korkoc. Prensa Académica (2003).

\(^{§}\)Es posible distinguir experimentalmente entre\(\eta=0.5\) y\(\eta=0\) eligiendo metales de contacto con diferentes funciones de trabajo. Si se observa que la brecha de conductancia cambia entonces no puede ser determinada por la brecha HOMO-LUMO, y por lo tanto\(\eta \neq 0\)