9.10: Máquinas de Polo Saliente- Teoría de Dos Reacciones

Hasta el momento, hemos estado describiendo lo que se conoce como máquinas de “rotor redondo”, en las que la reactancia del estator no depende de la posición del rotor. Esta es una aproximación bastante buena para generadores de turbina grandes y muchas máquinas bipolares más pequeñas, pero no es una buena aproximación para muchos motores síncronos ni para generadores de velocidad más lenta. Para muchas de estas aplicaciones es más rentable enrollar los conductores de campo alrededor de cuerpos de acero (llamados polos) que luego se sujetan al cuerpo del rotor, con pernos o juntas de cola de milano. Estos producen anisotropías magnéticas en la máquina que afectan su funcionamiento. La teoría que sigue es una introducción a la teoría de las dos reacciones y, en consecuencia, a las transformaciones de campo rotativo que forman la base de la mayoría de los análisis dinámicos modernos.

La Figura 8 muestra una imagen muy esquemática de la máquina de polos salientes, destinada principalmente a mostrar cómo enmarcar este análisis. Al igual que con la máquina de rotor redondo, el devanado del estator se encuentra en ranuras en la superficie de un anillo de núcleo de estator altamente permeable. El devanado de campo se enrolla alrededor de piezas polares de acero. Separamos la hoja de corriente del estator en dos componentes: uno alineado con y otro

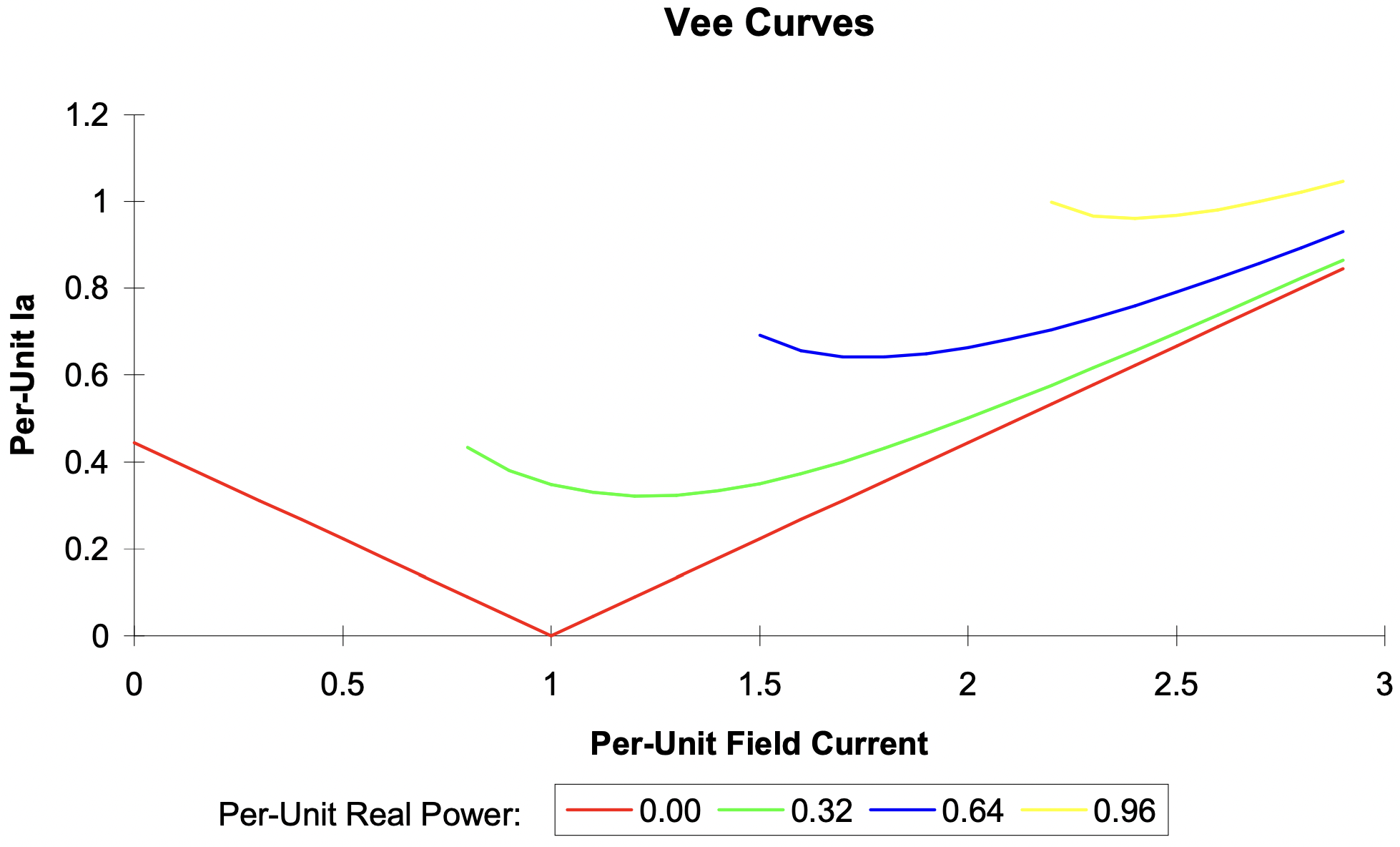Figura 7: Curva sincrónica de la máquina en V

en cuadratura al campo. Recuerde que estos dos componentes de corriente son en sí mismos combinaciones (lineales) de las corrientes de fase del estator. La transformación entre las corrientes de fase y los componentes del eje d y q es sencilla y aparecerá en el Capítulo 4 de estas notas.

La clave aquí es separar MMF y flujo en dos componentes ortogonales y pretender que cada uno puede ser tratado como sinusoidal. Los dos componentes están alineados con el eje directo y con el eje de cuadratura de la máquina. El eje directo está alineado con el devanado de campo, mientras que el eje de cuadratura conduce el directo 90 grados. Entonces, si\(\ \phi\) es el ángulo entre el eje directo y el eje de fase a, podemos escribir para la fase de enlace de flujo a:

\(\ \lambda_{a}=\lambda_{d} \cos \phi-\lambda_{q} \sin \phi\)

Entonces, en funcionamiento en estado estacionario, si\(\ V_{a}=\frac{d \lambda_{a}}{d t}\), y\(\ \phi=\omega t+\operatorname{delta}\),

\(\ V_{a}=-\omega \lambda_{d} \sin \phi-\omega \lambda_{q} \cos \phi\)

lo que nos permite definir:

\ (\\ begin {array} {l}
V_ {d} =-\ omega\ lambda_ {q}\\
V_ {q} =\ omega\ lambda_ {d}
\ end {array}\)

se podría pensar en el vector de 'voltaje' como liderando el vector de 'flujo' en 90 grados.

Ahora bien, si la máquina es lineal, esos flujos vienen dados por:

\ (\\ comenzar {alineado}
\ lambda_ {d} &=L_ {d} I_ {d} +M I_ {f}\
\ lambda_ {q} &=L_ {q} I_ {q}
\ final {alineado}\)

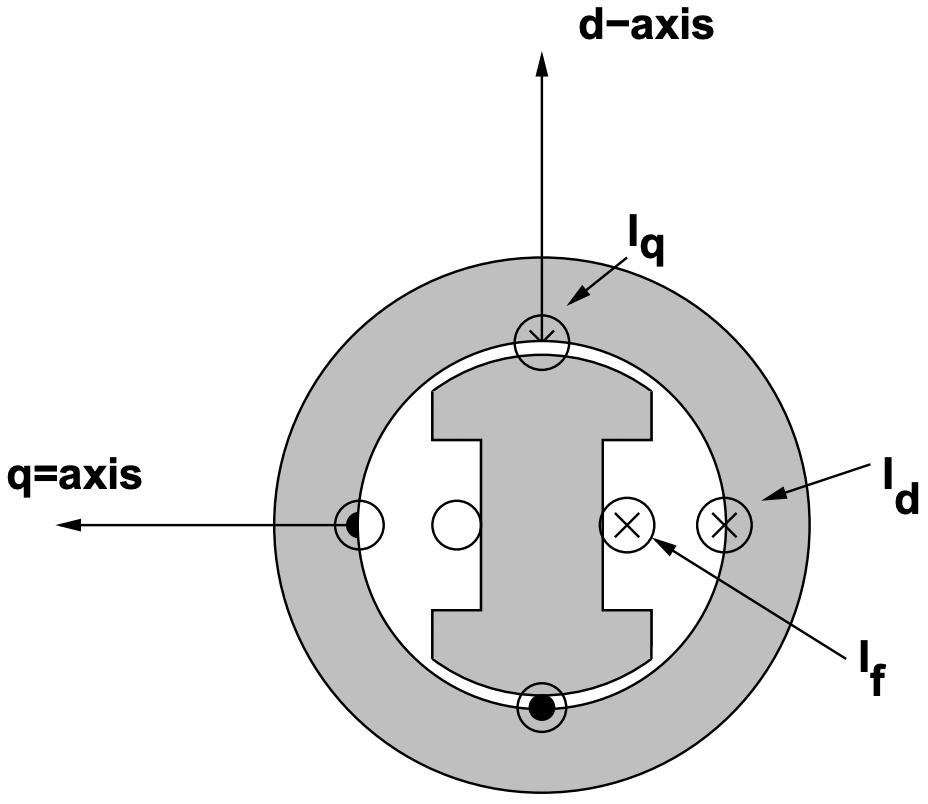Figura 8: Dibujos animados de una máquina síncrona de polos salientes

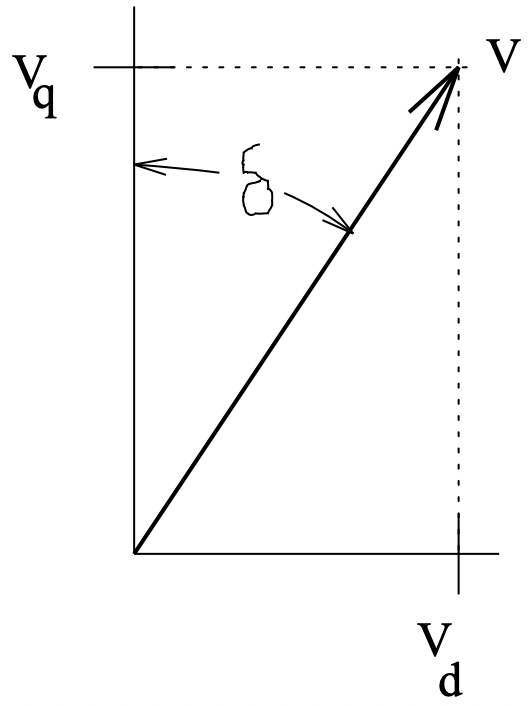Figura 9: Resolución del voltaje del terminal

Obsérvese que, en general,\(\ L_{d} \neq L_{q}\). En máquinas síncronas de campo herido, generalmente\(\ L_{d}>L_{q}\). Lo contrario es cierto para la mayoría de las máquinas de imanes permanentes salientes (imanes enterrados).

Haciendo referencia a la Figura 9, se puede resolver el voltaje terminal en estos componentes:

\ (\\ begin {array} {l}
V_ {d} =V\ sin\ delta\\
V_ {q} =V\ cos\ delta
\ end {array}\)

o:

\ (\\ comenzar {alineado}
V_ {d} &=-\ omega\ lambda_ {q} =-\ omega L_ {q} I_ {q} =V\ sin\ delta\\
V_ {q} &=\ omega\ lambda_ {d} =\ omega L_ {d} I_ {d} + omega\ M I_ {f} =V\ cos\ delta
\ fin alineado}\)

que se invierte fácilmente para producir:

\ (\\ comenzar {alineado}
I_ {d} &=\ frac {V\ cos\ delta-e_ {a f}} {X_ {d}}\\
I_ {q} &=-\ frac {V\ sin\ delta} {X_ {q}}
\ end {alineado}\)

donde

\(\ X_{d}=\omega L_{d} \quad X_{q}=\omega L_{q} \quad E_{a f}=\omega M I_{f}\)

Ahora, estamos trabajando en variables ordinarias (¡esta discusión debería ayudar a motivar el uso de la perunidad!) , y cada una de estas variables es la amplitud máxima. Entonces, si tomamos un marco de referencia complejo:

\ (\\ comenzar {alineado}
\ subrayado {V} &=V_ {d} +j V_ {q}\
\ subrayado {I} &=I_ {d} +j I_ {q}
\ end {alineado}\)

el poder complejo es:

\(\ P+j Q=\frac{3}{2} \underline{V I}^{*}=\frac{3}{2}\left\{\left(V_{d} I_{d}+V_{q} I_{q}\right)+j\left(V_{q} I_{d}-V_{d} I_{q}\right)\right\}\)

o:

\ (\\ comenzar {alineado}
P &=-\ frac {3} {2}\ izquierda (\ frac {V E_ {a f}} {X_ {d}}\ sin\ delta+\ frac {V^ {2}} {2}\ izquierda (\ frac {1} {X_ {d}} -\ frac {1} {X_ {q}} derecha)\ sin 2\ delta\ derecha)\\
Q &=\ frac {3} {2}\ izquierda (\ frac {V^ {2}} {2}\ izquierda (\ frac {1} {X_ {d}} +\ frac {1} {X_ {q}}\ derecha) -\ frac {V^ {2}} {2}\ izquierda (\ frac {1} {X_ { d}} -\ frac {1} {X_ {q}}\ derecha)\ cos 2\ delta-\ frac {V E_ {a f}} {X_ {d}}\ cos\ delta\ derecha)
\ final {alineado}\)

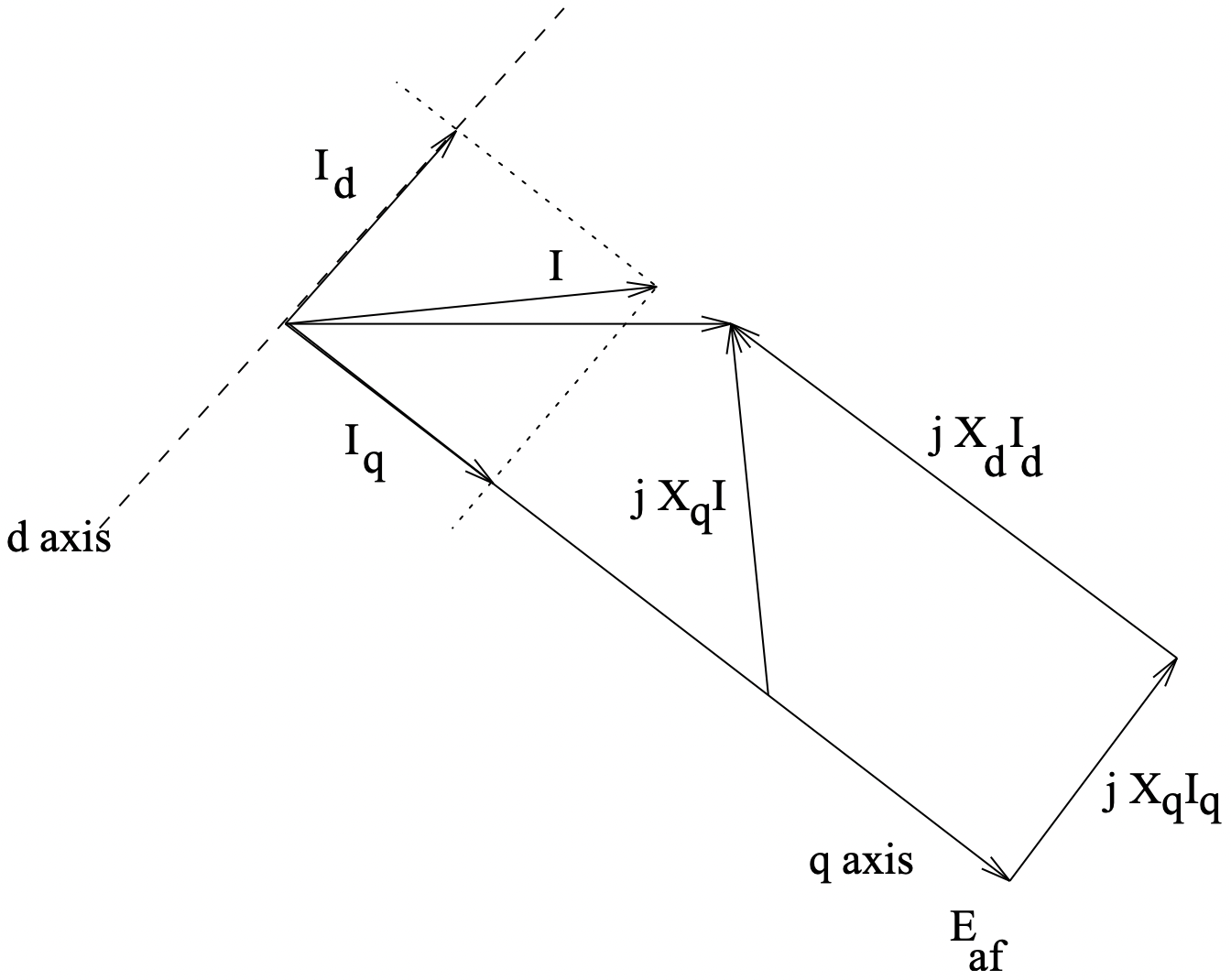Figura 10: Diagrama de fasores: Máquina de polos salientes

En la Figura 10 se muestra un diagrama de fasores para una máquina de polos salientes. Esto es un poco diferente de la imagen equivalente para una máquina de rotor redondo, en que la corriente del estator se ha separado en sus componentes de eje d y q, y las caídas de voltaje asociadas con esos componentes se han extraído por separado. Es interesante y útil reconocer que la tensión interna se\(\ E_{a f}\) puede expresar como:

\(\ E_{a f}=E_{1}+\left(X_{d}-X_{q}\right) I_{d}\)

donde el voltaje\(\ E_{1}\) está en el eje de cuadratura. De hecho, E1 sería el voltaje interno de una máquina de rotor redondo con reactancia\(\ X_{q}\) y la misma corriente de estator y voltaje de terminal. Entonces el punto de operación se encuentra con bastante facilidad:

\ (\\ begin {alineado}
\ delta &=-\ tan ^ {-1}\ izquierda (\ frac {X_ {q} I\ sin\ psi} {V+X_ {q} I\ cos\ psi}\ derecha)\\
E_ {1} &=\ sqrt {\ izquierda (V+X_ {q} I\ sin\ psi\ derecha) ^ {2} +\ izquierda (X_ _ {q} I\ cos\ psi\ derecha) ^ {2}}
\ fin {alineado}\)

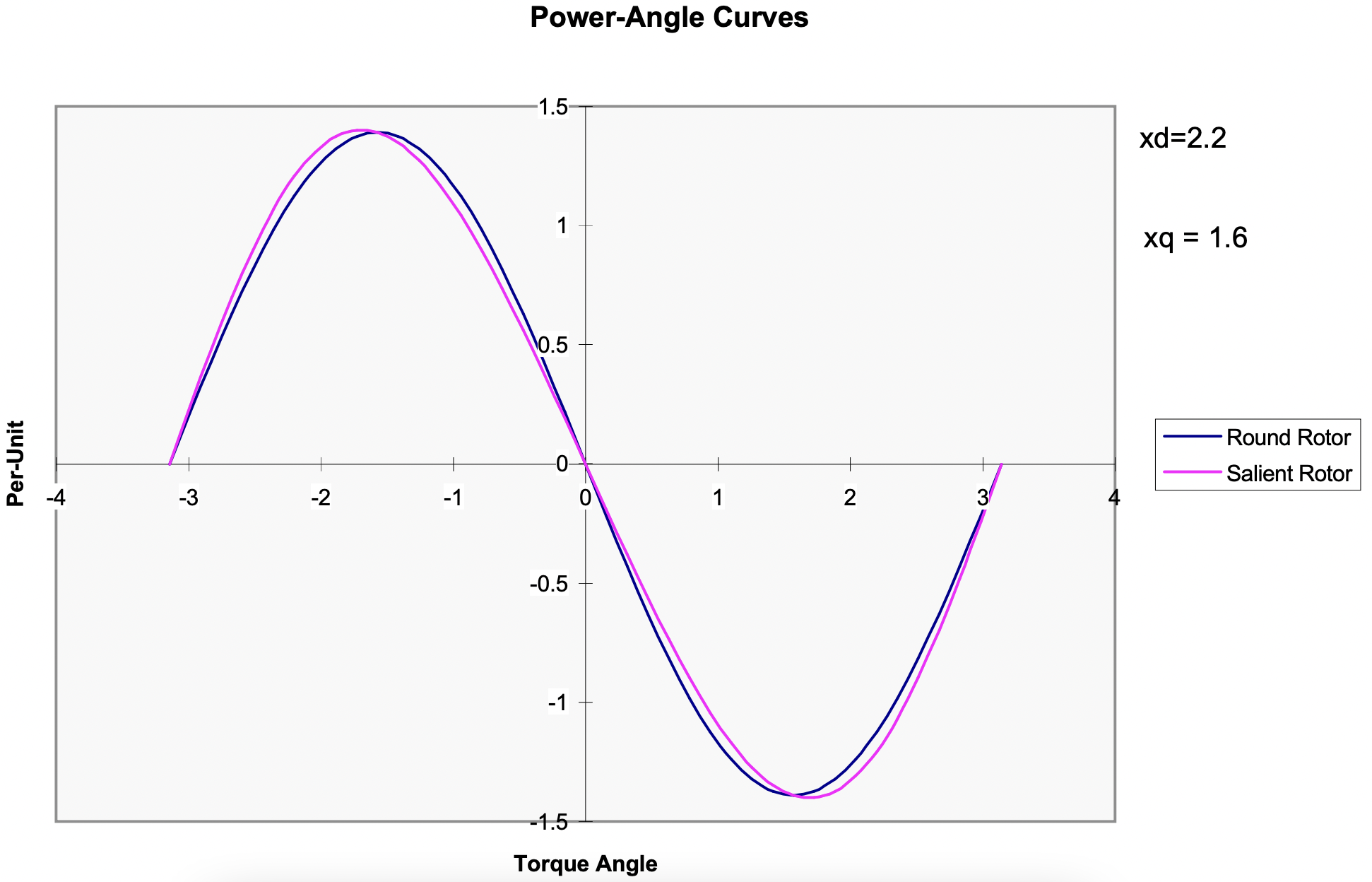Figura 11: Curvas de par-ángulo: Rotor Redondo y Máquinas de Polo Saliente

En la Figura 11 se muestra una comparación de curvas de par-ángulo para un par de máquinas, una con una redonda, otra con un rotor sobresaliente. No es demasiado difícil ver por qué los analistas de sistemas de energía a menudo descuidan la prominencia al hacer cosas como cálculos de estabilidad transitoria.