10.1: Modelo Transformador de Motor de Inducción

La máquina de inducción tiene dos elementos eléctricamente activos: un rotor y un estator. En funcionamiento normal, el estator es excitado por voltaje alterno. (Consideramos aquí solo máquinas polifásicas). La excitación del estator crea un campo magnético en forma de onda giratoria o itinerante, que induce corrientes en los circuitos del rotor. Esas corrientes, a su vez, interactúan con la onda viajera para producir torque. Para iniciar el análisis de esta máquina, supongamos que tanto el rotor como el estator pueden describirse mediante devanados balanceados, trifásicos. Los dos conjuntos están, por supuesto, acoplados por inductancias mutuas que dependen de la posición del rotor. Los flujos del estator son\(\ \left(\lambda_{a}, \lambda_{b}, \lambda_{c}\right)\) y los flujos del rotor son\(\ \left(\lambda_{A}, \lambda_{B}, \lambda_{C}\right)\). La relación flujo vs. corriente viene dada por:

\ (\\ left [\ begin {array} {c}
\ lambda_ {a}\\
\ lambda_ {b}\\
\ lambda_ {c}\\
\ lambda_ {A}\\
\ lambda_ {B}\
\ lambda_ {C}
\ end {array}\\ right] =\ left [\ begin {array} {ll}
\ subrayado {L} _ S} &\ subrayado {M} _ {S R}\\
\ subrayado {M} _ {S R} ^ {T} &\ subrayado {L} _ {R}
\ final {matriz}\ derecha]\ izquierda [\ comenzar {matriz} {c}
i_ {a}\\
i_ {b}\\
i_ {c}\\
i_ {A}\
i_ {B}\\
i_ {C}
\ i_ fin {matriz}\ derecha]\ etiqueta {1}\)

donde las matrices de componentes son:

\ (\\ subrayado {\ subrayado {L}} _ {S} =\ left [\ begin {array} {lll}
L_ {a} & L_ {a b} & L_ {a b}\\
L_ {a b} & L_ {a} & L_ {a} &
L_ {a b}\\ L_ {a b} & L_ {a}
fin {matriz}\ derecha]\ etiqueta {2}\)

\ (\\ subrayado {\ subrayado {L}} _ {R} =\ left [\ begin {array} {lll}
L_ {A} & L_ {A B} & L_ {A B}\\
L_ {A B} & L_ {A} & L_ {A} &
L_ {A B}\\ L_ {A B} & L_ {A}
final {matriz}\ derecha]\ etiqueta {3}\)

La parte de inductancia mutua de (1) es una matriz circulante:

\ (\\ subrayado {\ subrayado {M}} _ {S R} =\ izquierda [\ begin {array} {lll}
M\ cos (p\ theta) & M\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha) & M\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha)\\
M\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha) & M\ cos (p\ theta) & M\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha)\
M\ cos\ izquierda (p\ theta+\ frac {2\ pi} {3}\ derecha) & M\ cos\ izquierda (p\ theta-\ frac {2\ pi} {3}\ derecha) & M\ cos (p\ theta)
\ end {array}\ derecha]\ label {4}\)

Para llevar el análisis más allá, es necesario hacer algunas suposiciones respecto a la operación. Para comenzar, asuma corrientes equilibradas tanto en el estator como en el rotor:

\ (\\ begin {array} {l}
i_ {a} =I_ {S}\ cos (\ omega t)\\
i_ {b} =I_ {S}\ cos\ izquierda (\ omega t-\ frac {2\ pi} {3}\ derecha)\
i_ {c} =I_ {S}\ cos\ izquierda (\ omega t+\ frac {2\ pi} {3}\ derecha)
\ end {array}\ label {5}\)

\ (\\ comenzar {alineado}
i_ {A} &=I_ {R}\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R}\ derecha)\\
i_ {B} &=I_ {R}\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R} -\ frac {2\ pi} {3}\ derecha)\
i_ {C} &=I_ {R}\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R} +\ frac {2\ pi} {3}\ derecha)
\ final {alineado}\ etiqueta {6}\)

La posición del rotor se\(\ \theta\) puede describir mediante

\(\ \theta=\omega_{m} t+\theta_{0}\label{7}\)

Bajo estos supuestos, podemos calcular la forma de los flujos estatóricos. Resulta que solo necesitamos escribir las expresiones para\(\ \lambda_{a}\) y\(\ \lambda_{A}\) para ver qué está pasando:

\ (\\ comenzar {alineado}
\ lambda_ {a} =&\ izquierda (L_ {a} -L_ {a b}\ derecha) I_ {s}\ cos (\ omega t) +M I_ {R}\ izquierda (\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R}\ derecha)\ cos p\ izquierda (\ omega_ {m} +\ theta_ {0}\ derecho)\ derecho. \\
&+\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R} +\ frac {2\ pi} {3}\ derecha)\ cos\ izquierda (p\ izquierda (\ omega_ {m} t+\ theta_ {0}\ derecha) -\ frac {2\ pi} {3}\ derecha) +\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R} -\ frac {2\ pi} {3}\ derecha)\ cos\ izquierda (p\ izquierda (\ omega_ {m} t+\ theta_ {0}\ derecha) +\ frac {2\ pi} {3}\ derecha)
\ final {alineado}\ etiqueta {8 }\)

que, tras reducir algunas de las expresiones trig, se convierte en:

\(\ \lambda_{a}=\left(L_{a}-L_{a b}\right) I_{s} \cos (\omega t)+\frac{3}{2} M I_{R} \cos \left(\left(p \omega_{m}+\omega_{R}\right) t+\xi_{R}+p \theta_{0}\right)\label{9}\)

Hacer lo mismo para la fase A del rotor produce:

\ (\\ comenzar {alineado}
\ lambda_ {A} =& M I_ {s}\ izquierda (\ cos p\ izquierda (\ omega_ {m} t+\ theta_ {0}\ derecha)\ cos (\ omega t)\ derecha) +\ cos\ izquierda (p\ izquierda (\ omega_ {m} t+\ theta_ {0}\ derecha) -\ frac {2\ pi} {3}\ derecha)\ cos\ izquierda (\ omega t-\ frac {2\ pi} {3}\ derecha)\\
&+\ cos\ izquierda (p\ izquierda (\ omega_ {m} t+\ theta_ {0}\ derecha) +\ frac {2\ pi} {3}\ derecha)\ cos\ izquierda (\ omega t+\ frac {2\ pi} {3}\ derecha) +\ izquierda (L_ {A} -L_ {A B}\ derecha) I_ {R}\ cos\ izquierda (\ omega_ {R} t+\ xi_ {R}\ derecha)
\ final {alineado}\ etiqueta 10}\)

Esta última expresión es, después de manipular:

\(\ \lambda_{A}=\frac{3}{2} M I_{s} \cos \left(\left(\omega-p \omega_{m}\right) t-p \theta_{0}\right)+\left(L_{A}-L_{A B}\right) I_{R} \cos \left(\omega_{R} t+\xi_{R}\right)\label{11}\)

Estas dos expresiones, 9 y 11 dan expresiones para flujos en la armadura y devanados del rotor en términos de corrientes en los mismos dos devanados, asumiendo que ambas distribuciones de corriente son sinusoidales en tiempo y espacio y representan distribuciones equilibradas. El siguiente paso es hacer otra suposición, que las frecuencias del estator y del rotor coinciden a través de la rotación del rotor. Es decir:

\(\ \omega-p \omega_{m}=\omega_{R}\label{12}\)

Es importante mantener rectas las diferentes frecuencias aquí:

\(\ \omega\)es la frecuencia eléctrica del estator

\(\ \omega_{R}\)es la frecuencia eléctrica del rotor

\(\ \omega_{m}\)es la velocidad de rotación mecánica

así que esa\(\ p \omega_{m}\) es la velocidad de rotación eléctrica.

Para referir las cantidades del rotor al bastidor del estator (es decir, no giratorio), y para trabajar en amplitudes complejas, se hacen las siguientes definiciones:

\(\ \lambda_{a}=\operatorname{Re}\left(\underline{\Lambda}_{a} e^{j \omega t}\right)\label{13}\)

\(\ \lambda_{A}=\operatorname{Re}\left(\underline{\Lambda}_{A} e^{j \omega_{R} t}\right)\label{14}\)

\(\ i_{a}=\operatorname{Re}\left(\underline{I}_{a} e^{j \omega t}\right)\label{15}\)

\(\ i_{A}=\operatorname{Re}\left(\underline{I}_{A} e^{j \omega_{R} t}\right)\label{16}\)

Con estas definiciones, las complejas amplitudes plasmadas en 58 y 66 se convierten en:

\(\ \underline{\Lambda}_{a}=L_{S} \underline{I}_{a}+\frac{3}{2} M \underline{I}_{A} e^{j\left(\xi_{R}+p \theta_{0}\right)}\label{17}\)

\(\ \underline{\Lambda}_{A}=\frac{3}{2} M \underline{I}_{a} e^{-j p \theta_{0}}+L_{R} \underline{I}_{A} e^{j \xi_{R}}\label{18}\)

Hay dos ángulos de fase incrustados en estas expresiones:\(\ \theta_{0}\) que describe el ángulo de fase físico del rotor con respecto a la corriente del estator y\(\ \xi_{R}\) que describe el ángulo de fase de las corrientes del rotor con respecto a las corrientes del estator. Por este medio inventamos dos nuevas variables del rotor:

\(\ \left.\underline{\Lambda}_{A R}=\underline{\Lambda}_{A} e^{j p \theta}\right)\label{19}\)

\(\ \underline{I}_{A R}=\underline{I}_{A} e^{j\left(p \theta_{0}+\xi_{R}\right)}\label{20}\)

Estos son el flujo del rotor y la corriente referidos al ángulo de fase de la armadura. Tenga en cuenta que\(\ \underline{\Lambda}_{A R}\) y\(\ \underline{I}_{A R}\) tener la misma relación de fase entre sí como hacer\(\ \underline{\Lambda}_{A}\) y\(\ \underline{I}_{A}\). Usando 19 y 20 en 17 y 18, la relación flujo/corriente básica para la máquina de inducción se convierte en:

\ (\\ left [\ begin {array} {l}
\ subrayado {\ Lambda} _ {a}
\\\ subrayado {\ lambda} _ {A R}
\ end {array}\ right] =\ left [\ begin {array} {ll}
L_ {S} &\ frac {3} {2} M\
\ frac {3} {2} M y L_ {R}
\ end {array}\ right]\ left [\ begin {array} {l}
\ subrayado {I} _ {a}\\
\ subrayado {I} _ _ {A R}
\ end {array}\ derecha]\ label {21}\)

Esta es una declaración monofásica equivalente, que describe la relación flujo/corriente en la fase a, asumiendo una operación equilibrada. La misma expresión describirá las fases b y c.

El voltaje en los terminales de los devanados del estator y del rotor (posiblemente equivalente) es, entonces:

\(\ \underline{V}_{a}=j \omega \underline{\Lambda}_{a}+R_{a} \underline{I}_{a}\label{22}\)

\(\ \underline{V}_{A R}=j \omega_{R} \underline{\Lambda}_{A R}+R_{A} \underline{I}_{A R}\label{23}\)

o:

\(\ \underline{V}_{a}=j \omega L_{S} \underline{I}_{a}+j \omega \frac{3}{2} M \underline{I}_{A R}+R_{a} \underline{I}_{a}\label{24}\)

\(\ \underline{V}_{A R}=j \omega_{R} \frac{3}{2} M \underline{I}_{a}+j \omega_{R} L_{R} \underline{I}_{A R}+R_{A} \underline{I}_{A R}\label{25}\)

Para llevar esto más lejos, es necesario profundizar un poco más en los parámetros de la máquina. Tenga en cuenta que\(\ L_{S}\) y\(\ L_{R}\) son inductancias sincrónicas para el estator y el rotor. Estos pueden separarse en componentes fundamentales del espacio y de “fuga” de la siguiente manera:

\(\ L_{S}=L_{a}-L_{a b}=\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} R l N_{S}^{2} k_{S}^{2}}{p^{2} g}+L_{S l}\label{26}\)

\(\ L_{R}=L_{A}-L_{A B}=\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} R l N_{R}^{2} k_{R}^{2}}{p^{2} g}+L_{R l}\label{27}\)

Donde se mantiene el conjunto normal de parámetros de la máquina:

\(\ R\)es el radio del rotor

\(\ l\)es longitud activa

\(\ g\)es el espacio de aire efectivo

\(\ p\)es el número de pares de polos

\(\ N\)representa el número de vueltas

\(\ k\)representa el factor de bobinado

\(\ S\)como subíndice se refiere al estator

\(\ R\)como subíndice se refiere al rotor

\(\ L_{l}\)es inductancia de “fuga”

Los dos términos de fuga\(\ L_{S l}\) y\(\ L_{R l}\) contienen inductancias armónicas de estator y rotor de orden superior, inductancias de ranura, inductancias de devanado final y, si es necesario, una provisión para la inclinación del rotor. Esencialmente, se utilizan para representar todo el flujo en el rotor y estator que no está mutuamente acoplado.

En los mismos términos, la inductancia mutua de estator a rotor, que se toma para comprender solo un término fundamental espacial, es:

\(\ M=\frac{4}{\pi} \frac{\mu_{0} R l N_{S} N_{R} k_{S} k_{R}}{p^{2} g}\label{28}\)

Obsérvese que existen, por supuesto, vínculos de flujo mutuo armónicos espaciales. Si se incluyeran, cabellarían el análisis sustancialmente. Los ignoramos aquí y notamos que sí tienen un efecto en el comportamiento de la máquina, pero ese efecto es de segundo orden.

La permeancia del entrehierro se define como:

\(\ \wp_{a g}=\frac{4}{\pi} \frac{\mu_{0} R l}{p^{2} g}\label{29}\)

para que las inductancias sean:

\(\ L_{S}=\frac{3}{2} \wp_{a g} k_{S}^{2} N_{S}^{2}+L_{S l}\label{30}\)

\(\ L_{R}=\frac{3}{2} \wp_{a g} k_{R}^{2} N_{R}^{2}+L_{R l}\label{31}\)

\(\ M=\wp_{a g} N_{S} N_{R} k_{S} k_{R}\label{32}\)

Aquí definimos “slip” s por:

\(\ \omega_{R}=s \omega\label{33}\)

para que

\(\ s=1-\frac{p \omega_{m}}{\omega}\label{34}\)

Entonces las ecuaciones de balance de voltaje se convierten en:

\(\ \underline{V}_{a}=j \omega\left(\frac{3}{2} \wp_{a g} k_{S}^{2} N_{S}^{2}+L_{S l}\right) \underline{I}_{a}+j \omega \frac{3}{2} \wp_{a g} N_{S} N_{R} k_{S} k_{R} \underline{I}_{A R}+R_{a} \underline{I}_{a}\label{35}\)

\(\ \underline{V}_{A R}=j s \omega \frac{3}{2} \wp_{a g} N_{S} N_{R} k_{S} k_{R} \underline{I}_{a}+j s \omega\left(\frac{3}{2} \wp_{a g} k_{R}^{2} N_{R}^{2}+L_{R l}\right) \underline{I}_{A R}+R_{A} \underline{I}_{A R}\label{36}\)

En este punto, estamos listos para definir la corriente del rotor referida al estator. Esto se hace asumiendo una relación de vueltas efectiva que, a su vez, define una corriente de estator equivalente para producir el mismo MMF fundamental que una corriente de rotor dada:

\(\ \underline{I}_{2}=\frac{N_{R} k_{R}}{N_{S} k_{S}} \underline{I}_{A R}\label{37}\)

Ahora bien, si asumimos que el rotor de la máquina está cortocircuitado para que V AR = 0 y hacemos alguna manipulación obtenemos:

\(\ \underline{V}_{a}=j\left(X_{M}+X_{1}\right) \underline{I}_{a}+j X_{M} \underline{I}_{2}+R_{a} \underline{I}_{a}\label{38}\)

\(\ 0=j X_{M} \underline{I}_{a}+j\left(X_{M}+X_{2}\right) \underline{I}_{2}+\frac{R_{2}}{s} \underline{I}_{2}\label{39}\)

donde se hayan hecho las siguientes definiciones:

\(\ X_{M}=\frac{3}{2} \omega \wp_{a g} N_{S}^{2} k_{S}^{2}\label{40}\)

\(\ X_{1}=\omega L_{S l}\label{41}\)

\(\ X_{2}=\omega L_{R l}\left(\frac{N_{S} k_{S}}{N_{R} k_{R}}\right)^{2}\label{42}\)

\(\ R_{2}=R_{A}\left(\frac{N_{S} k_{S}}{N_{R} k_{R}}\right)^{2}\label{43}\)

Estas expresiones describen un circuito equivalente simple para el espectáculo de inducción en la Figura 2. Amplificaremos en este circuito equivalente anon.

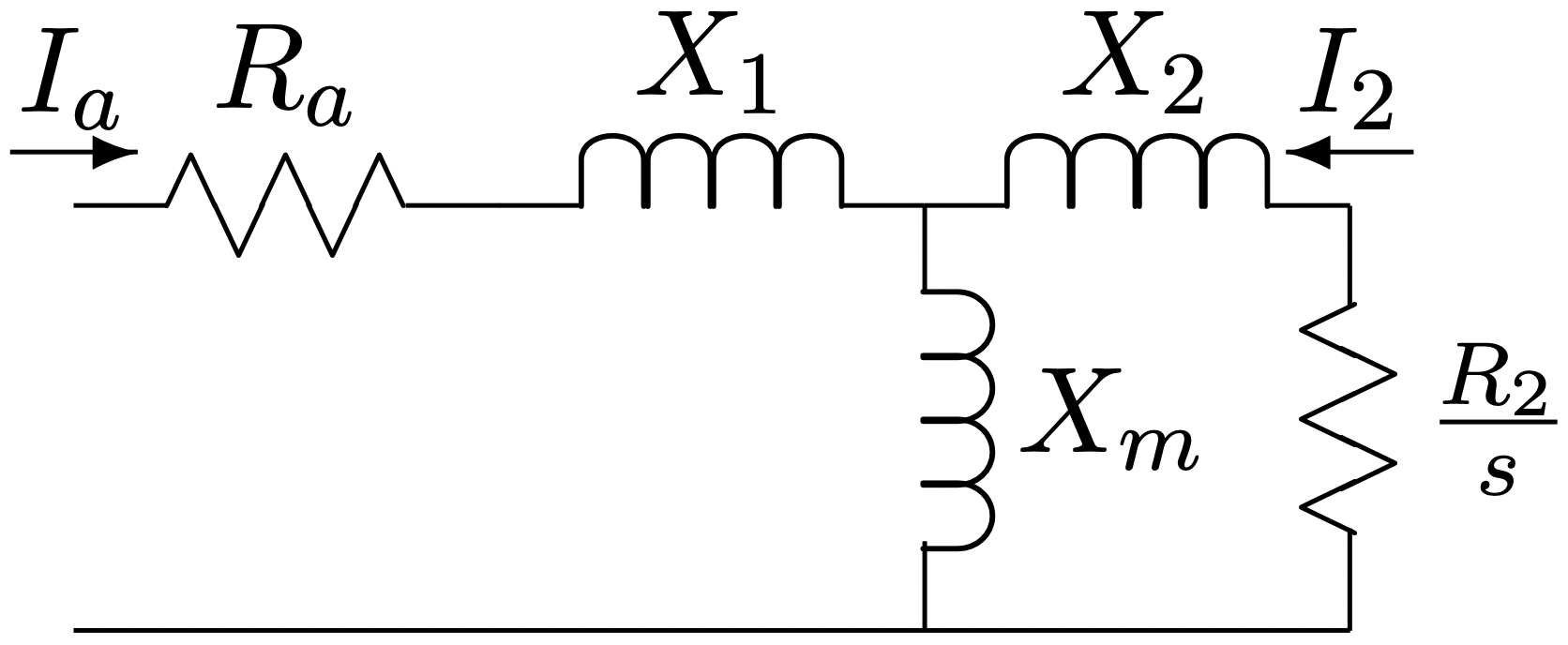Figura 2: Circuito equivalente

Espacio de aire efectivo: Coeficiente de Carter

En los motores de inducción, donde el entrehierro suele ser bastante pequeño, es necesario corregir la permeancia del entrehierro para el efecto de las aberturas de las ranuras. Estos hacen que la permeancia del entrehierro sea ligeramente menor que la calculada a partir de la brecha física, lo que efectivamente hace que la brecha sea un poco más grande. La relación entre la brecha efectiva y física es:

\(\ g_{\mathrm{eff}}=g \frac{t+s}{t+s-g f(\alpha)}\label{44}\)

donde

\(\ f(\alpha)=f\left(\frac{s}{2 g}\right)=\alpha \tan (\alpha)-\log \sec \alpha\label{45}\)