10.3: Modelo de Máquina de Jaula de Ardilla

Ahora derivamos un modelo de circuito para el motor de jaula de ardilla utilizando técnicas analíticas de campo. El modelo consta de dos partes principales. El primero de ellos es una descripción del flujo del estator en términos de corrientes de estator y rotor. El segundo es una descripción de la corriente del rotor en términos de flujo de entrehierro. El resultado de todo esto es un conjunto de expresiones para los elementos del modelo de circuito para la máquina de inducción.

Para comenzar, supongamos que el rotor es lo suficientemente simétrico como para llevar una corriente superficial, cuya fundamental es:

\ (\\ comenzar {alineado}
\ bar {K} _ {r} &=\ bar {\ imath} _ {z}\ nombreoperador {Re}\ izquierda (\ subrayado {K} _ _ {r} e^ {j\ izquierda (s\ omega t-p\ phi^ {\ prime}\ derecha)}\ derecha)\\
&=\ bar {\ imath} _ {z}\ operador nombre {Re}\ izquierda (\ subrayado {K} _ {r} e^ {j (\ omega t-p\ phi)}\ derecha)
\ final {alineado}\ etiqueta {58}\ )

Tenga en cuenta que en 58 hemos hecho uso de la simple transformación entre las coordenadas del rotor y el estator:

\(\ \phi^{\prime}=\phi-\omega_{m} t\label{59}\)

y que

\(\ p \omega_{m}=\omega-\omega_{r}=\omega(1-s)\label{60}\)

Aquí, hemos utilizado los siguientes símbolos:

\(\ \underline{K}_{r}\)	es la amplitud compleja de la corriente superficial del rotor
\(\ \mathcal{S}\)	es por unidad de “deslizamiento”
\(\ \omega\)	es la frecuencia eléctrica del estator
\(\ \omega_{r}\)	es la frecuencia eléctrica del rotor
\(\ \omega_{m}\)	es la velocidad de rotación

La corriente del rotor producirá una densidad de flujo de entrehierro de la forma:

\(\ B_{r}=R e\left(\underline{B}_{r} e^{j(\omega t-p \phi)}\right)\label{61}\)

donde

\(\ \underline{B}_{r}=-j \mu_{0} \frac{R}{p g} \underline{K}_{r}\label{62}\)

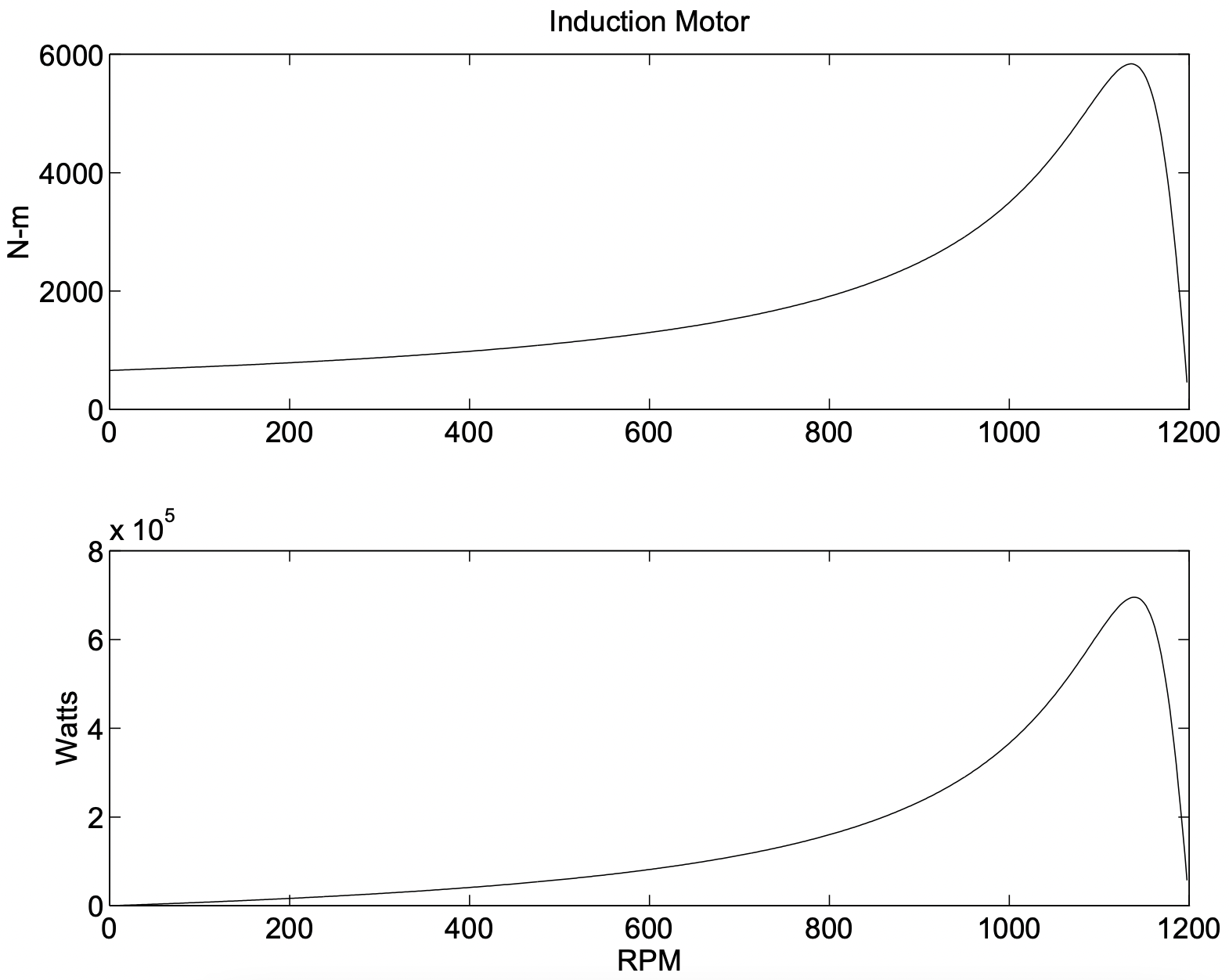Figura 3: Par de torsión y potencia frente a velocidad para motor de ejemplo

Tenga en cuenta que esto describe solo la densidad de flujo magnético radial producida por el espacio fundamental de la corriente del rotor. El flujo unido por el devanado de la armadura debido a esta densidad de flujo es:

\(\ \lambda_{A R}=l N_{S} k_{S} \int_{-\frac{\pi}{p}}^{0} B_{r}(\phi) R d \phi\label{63}\)

Esto produce una amplitud compleja para\(\ \lambda_{A R}\):

\(\ \lambda_{A R}=\operatorname{Re}\left(\underline{\Lambda}_{A R} e^{j \omega t}\right)\label{64}\)

donde

\(\ \underline{\Lambda}_{A R}=\frac{2 l \mu_{0} R^{2} N_{S} k_{S}}{p^{2} g} \underline{K}_{r}\label{65}\)

Añadiendo esto al flujo producido por las corrientes del estator, tenemos una expresión para el flujo total del estator:

\(\ \underline{\Lambda}_{a}=\left(\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} N_{S}^{2} R l k_{S}^{2}}{p^{2} g}+L_{S l}\right) \underline{I}_{a}+\frac{2 l \mu_{0} R^{2} N_{S} k_{S}}{p^{2} g} \underline{K}_{r}\label{66}\)

La expresión 66 motiva una definición de una corriente de rotor equivalente I2 en términos del espacio fundamental de la densidad de corriente superficial del rotor:

\(\ \underline{I}_{2}=\frac{\pi}{3} \frac{R}{N_{S} k_{S}} \underline{K}_{z}\label{67}\)

Luego tenemos la expresión simple para el flujo del estator:

\(\ \underline{\Lambda}_{a}=\left(L_{a d}+L_{S l}\right) \underline{I}_{a}+L_{a d} \underline{I}_{2}\label{68}\)

donde\(\ L_{a d}\) es el componente armónico espacial fundamental de la inductancia del estator:

\(\ L_{a d}=\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} N_{S}^{2} k_{S}^{2} R l}{p^{2} g}\label{69}\)

La segunda parte de esta derivación es el equivalente a encontrar una relación entre el flujo del rotor y\(\ I_{2}\). Sin embargo, dado que esta máquina no tiene devanados discretos, debemos enfocarnos en las barras individuales del rotor.

Supongamos que hay\(\ N_{R}\) ranuras en el rotor. Cada una de estas ranuras lleva algo de corriente. Si la máquina es simétrica y opera con corrientes balanceadas, podemos escribir una expresión para corriente en la\(\ k^{t h}\) ranura como:

\(\ i_{k}=\operatorname{Re}\left(\underline{I}_{k} e^{j s \omega t}\right)\label{70}\)

donde

\(\ \underline{I}_{k}=\underline{I} e^{-j \frac{2 \pi p}{N_{R}}}\label{71}\)

y\(\ \underline{I}\) es la amplitud compleja de la corriente en la ranura número cero. La expresión 71 muestra una progresión uniforme de la fase de corriente del rotor alrededor del rotor. Todas las ranuras del rotor llevan la misma corriente, pero esa corriente es retardada de fase (retardada) de ranura a ranura debido a la rotación relativa de la onda de corriente a la frecuencia de deslizamiento.

La densidad de corriente del rotor se puede expresar como una suma de impulsos:

\(\ K_{z}=R e\left(\sum_{k=0}^{N_{R}-1} \frac{1}{R} \underline{I} e^{j\left(\omega_{r} t-k \frac{2 \pi p}{N_{R}}\right)} \delta\left(\phi^{\prime}-\frac{2 \pi k}{N_{R}}\right)\right)\label{72}\)

La función de impulso unitario\(\ \delta()\) es nuestra manera de aproximar la corriente del rotor como una serie de corrientes impulsivas alrededor del rotor.

Esta corriente superficial del rotor puede expresarse como una serie de ondas viajeras de Fourier:

\(\ K_{z}=\operatorname{Re}\left(\sum_{n=-\infty}^{\infty} \underline{K}_{n} e^{j\left(\omega_{r} t-n p \phi^{\prime}\right)}\right)\label{73}\)

Tenga en cuenta que en 73, estamos permitiendo valores negativos del índice armónico espacial\(\ n\) para permitir ondas giratorias inversas. Esto es realmente parte de una expansión tanto en el tiempo como en el espacio, aunque solo estamos considerando la parte fundamental del tiempo. Podemos recuperar el componente armónico\(\ n^{t h}\) espacial de 73 empleando la siguiente fórmula:

\(\ \underline{K}_{n}=<\frac{1}{\pi} \int_{0}^{2 \pi} K_{r}(\phi, t) e^{-j\left(\omega_{r} t-n p \phi\right)} d \phi>\label{74}\)

Aquí los paréntesis <> denotan el promedio del tiempo y están aquí debido a la naturaleza bidimensional de la expansión. Para llevar a cabo 74 en 72, primero expanda 72 en sus partes conjugadas complejas:

\(\ K_{r}=\frac{1}{2} \sum_{k=0}^{N_{R}-1}\left\{\frac{\underline{I}}{R} e^{j\left(\omega_{r} t-k \frac{2 \pi p}{N_{R}}\right)}+\frac{\underline{I}^{*}}{R} e^{-j\left(\omega_{r} t-k \frac{2 \pi p}{N_{R}}\right)}\right\} \delta\left(\phi^{\prime}-\frac{2 \pi k}{N_{R}}\right)\label{75}\)

Si se usa 75 en 74, la segunda mitad de 75 da como resultado una suma de términos que el tiempo promedio a cero. La primera mitad de la expresión da como resultado:

\(\ \underline{K}_{n}=\frac{I}{2 \pi R} \int_{0}^{2 \pi} \sum_{k=0}^{N_{R}-1} e^{-j \frac{2 \pi p k}{N_{R}}} e^{j n p \phi} \delta\left(\phi-\frac{2 \pi k}{N_{R}}\right) d \phi\label{76}\)

La función de impulso convierte la integral en una evaluación del resto del integrando al impulso. Lo que queda es la suma:

\(\ \underline{K}_{n}=\frac{\underline{I}}{2 \pi R} \sum_{k=0}^{N_{R}-1} e^{j(n-1) \frac{2 \pi k p}{N_{R}}}\label{77}\)

La suma en 77 es fácilmente evaluada. Es:

\ (\\ sum_ {k=0} ^ {N_ {R} -1} e^ {j\ frac {2\ pi k p (n-1)} {N_ {R}}} =\ left\ {\ begin {array} {ll}
N_ {R} &\ text {if} (n-1)\ frac {P} {N_ {R}} =\ texto {entero}\\
0 &\ text {de lo contrario}
\ end {array}\ right. \ label {78}\)

El número entero en 78 puede ser positivo, negativo o cero. Resulta que solo los tres primeros de estos (cero, más y menos uno) son importantes, porque estos producen los mayores campos magnéticos y por lo tanto flujos. Estos son:

\ (\\ comenzar {alineado}
(n-1)\ frac {p} {N_ {R}} =-1 &\ texto {o} n=-\ frac {N_ {R} -p} {p}\\
=0\ quad &\ texto {o} n=1\\
=1\ cuádruple &\ texto {o} n=\ frac {N_ {R} +p} {p}
\ final {alineado}\ etiqueta {79}\)

Tenga en cuenta que 79 parece producir órdenes armónicas espaciales que pueden ser de orden no entero. Esto no es realmente cierto: es necesario que\(\ np\) sea un entero, y 79 siempre cumplirá esa condición.

Entonces, los órdenes armónicos de interés para nosotros son uno y

\(\ n_{+}=\frac{N_{R}}{p}+1\label{80}\)

\(\ n_{-}=-\left(\frac{N_{R}}{p}-1\right)\label{81}\)

Cada uno de los armónicos espaciales de la corriente de la jaula de ardilla producirá densidad de flujo radial. Una corriente superficial de la forma:

\(\ K_{n}=R e\left(\frac{N_{R} \underline{I}}{2 \pi R} e^{j\left(\omega_{r} t-n p \phi^{\prime}\right)}\right)\label{82}\)

produce densidad de flujo magnético radial:

\(\ B_{r n}=\operatorname{Re}\left(\underline{B}_{r n} e^{j\left(\omega_{r} t-n p \phi^{\prime}\right)}\right)\label{83}\)

donde

\(\ \underline{B}_{r n}=-j \frac{\mu_{0} N_{R} \underline{I}}{2 \pi n p g}\label{84}\)

A su vez, cada uno de los componentes de densidad de flujo radial producirá un componente de voltaje inducido. Para calcularlo, debemos invocar la ley de Faraday:

\(\ \nabla \times \bar{E}=-\frac{\partial \bar{B}}{\partial t}\label{85}\)

El componente radial de 85, asumiendo que los campos no varían con\(\ Z\), es:

\(\ \frac{1}{R} \frac{\partial}{\partial \phi} E_{z}=-\frac{\partial B_{r}}{\partial t}\label{86}\)

O, suponiendo un componente de campo eléctrico de la forma:

\(\ E_{z n}=\operatorname{Re}\left(\underline{E}_{n} e^{j\left(\omega_{r} t-n p \phi\right)}\right)\label{87}\)

Usando 84 y 87 en 86, obtenemos una expresión para el campo eléctrico inducido por componentes del flujo de separación de aire:

\(\ \underline{E}_{n}=\frac{\omega_{r} R}{n p} \underline{B}_{n}\label{88}\)

\(\ \underline{E}_{n}=-j \frac{\mu_{0} N_{R} \omega_{r} R}{2 \pi g(n p)^{2}} \underline{I}\label{89}\)

Ahora, el voltaje total inducido en una ranura empuja la corriente a través de los conductores en esa ranura. Podemos expresarlo por:

\(\ \underline{E}_{1}+\underline{E}_{n-}+\underline{E}_{n+}=\underline{Z}_{s l o t} \underline{I}\label{90}\)

Ahora: en 90, hay tres componentes del campo de entrehierro. \(\ E_{1}\)es el campo fundamental espacial, producido por el espacio fundamental de la corriente del rotor así como por el espacio fundamental de la corriente del estator. Los otros dos componentes a la izquierda de 90 son producidos solo por las corrientes del rotor y en realidad representan una impedancia reactiva adicional al rotor. Esto a menudo se llama inductancia de fuga en zigzag. El parámetro Zslot representa la impedancia de la propia ranura: resistencia y reactancia asociadas con campos magnéticos de ranura cruzada. Entonces 90 se pueden reescribir como:

\(\ \underline{E}_{1}=\underline{Z}_{s l o t} \underline{I}+j \frac{\mu_{0} N_{R} \omega_{r} R}{2 \pi g}\left(\frac{1}{\left(n_{+} p\right)^{2}}+\frac{1}{\left(n_{-} p\right)^{2}}\right) \underline{I}\label{91}\)

Para terminar este modelo, es necesario trasladar 91 de nuevo al estator. Ver que 67 y 77 hacen el vínculo entre\(\ \underline{I}\) y\(\ \underline{I}_{2}\):

\(\ \underline{I}_{2}=\frac{N_{R}}{6 N_{S} k_{S}} \underline{I}\label{92}\)

Entonces el campo eléctrico en la superficie del rotor es:

\(\ \underline{E}_{1}=\left[\frac{6 N_{S} k_{S}}{N_{R}} \underline{Z}_{s l o t}+j \omega_{r} \frac{3}{\pi} \frac{\mu_{0} N_{S} k_{S} R}{g}\left(\frac{1}{\left(n_{+} p\right)^{2}}+\frac{1}{\left(n_{-} p\right)^{2}}\right)\right] \underline{I}_{2}\label{93}\)

Esto debe traducirse en un voltaje equivalente del estator. Para ello, usamos 88 para traducir 93 en una declaración de campo magnético radial, luego encontramos el flujo gustado y de ahí el voltaje del estator a partir de eso. La densidad de flujo magnético es:

\ (\\ comenzar {alineado}
\ subrayado {B} _ {r} &=\ frac {p\ subrayado {E} _ {1}} {\ omega_ {r} R}\\
&=\ izquierda [\ frac {6 N_ {S} k_ {S} p} {N_ {R} R}\ izquierda (\ frac {R_ {s l o t} {\ omega_ {r}} +j L_ {s l o t}\ derecha) +j\ frac {3} {\ pi}\ frac {\ mu_ {0} N_ {S} k_ {S} p} {g}\ izquierda (\ frac {1} {\ izquierda (n_ {+} p\ derecha) ^ {2}} +\ frac {1 } {\ izquierda (n_ {-} p\ derecha) ^ {2}}\ derecha)\ derecha]\ subrayado {I} _ {2}
\ final {alineado}\ etiqueta {94}\)

donde la impedancia de ranura ha sido expresada por sus partes real e imaginaria:

\[\ \underline{Z}_{s l o t}=R_{s l o t}+j \omega_{r} L_{s l o t}\label{95} \]

El flujo que une el devanado de la armadura es:

\[\ \lambda_{a g}=N_{S} k_{S} l R \int_{-\frac{\pi}{2 p}}^{0} \operatorname{Re}\left(\underline{B}_{r} e^{j(\omega t-p \phi)}\right) d \phi\label{96} \]

Que se convierte en:

\[\ \lambda_{a g}=\operatorname{Re}\left(\underline{\Lambda}_{a g} e^{j \omega t}\right)\label{97} \]

donde:

\[\ \underline{\Lambda}_{a g}=j \frac{2 N_{S} k_{S} l R}{p} \underline{B}_{r}\label{98} \]

Entonces el voltaje de “entrehierro” es:

\ [\\ comenzar {alineado}
\ subrayado {V} _ {a g} &=j\ omega\ subrayado {\ Lambda} _ {a g} =-\ frac {2\ omega N_ {S} k_ {S} l R} {p}\ subrayado {B} _ _ {r}\
&=-\ subrayado {I} _ {2}\ izquierda [\ frac {12 l N_ {S} ^ {2} k_ {S} ^ {2}} {N_ {R}}\ izquierda (j\ omega L_ {s l o t} +\ frac {R_ {2}} {s}\ derecha) +j\ omega\ frac {6} {\ pi}\ frac {\ mu_ {0} R l N_ {S} ^ {2} k_ {S} ^ {2}} {g}\ izquierda (\ frac {1} {\ izquierda (n_ {+} p\ derecha) ^ {2}} +\ frac {1} {\ izquierda (n_ {-} p\ derecha) ^ {2}}\ derecha)\ derecha]
\ fin {alineado}\ label {99}\]

La expresión 99 describe la relación entre el voltaje fundamental del espacio de separación de aire\(\ \underline{V}_{a g}\) y la corriente del rotor\(\ \underline{I}_{2}\). Esta expresión se ajusta al circuito equivalente de la Figura 4 si las definiciones hechas a continuación se mantienen:

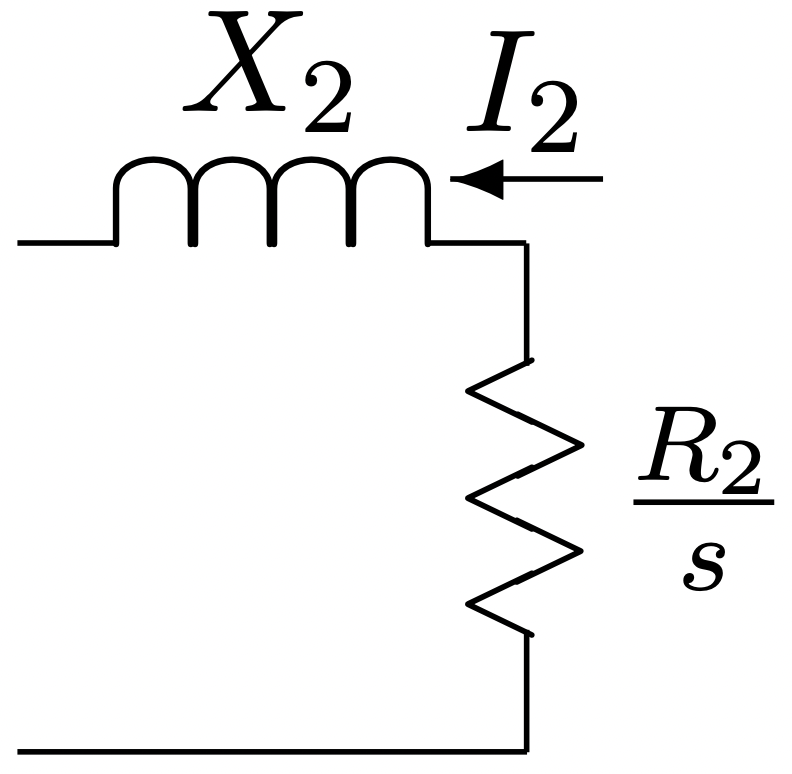Figura 4: Circuito Equivalente al Rotor

\[\ X_{2}=\omega \frac{12 l N_{S}^{2} k_{S}^{2}}{N_{R}} L_{\mathrm{slot}}+\omega \frac{6}{\pi} \frac{\mu_{0} R l N_{S}^{2} k_{S}^{2}}{g}\left(\frac{1}{\left(N_{R}+p\right)^{2}}+\frac{1}{\left(N_{R}-p\right)^{2}}\right)\label{100} \]

\[\ R_{2}=\frac{12 l N_{S}^{2} k_{S}^{2}}{N_{R}} R_{\text {slot }}\label{101} \]

El primer término en 100 expresa inductancia de fuga de ranura para el rotor. De manera similar, 101 expresa la resistencia del rotor en términos de resistencia de ranura. Tenga en cuenta que Lslot y Rslot se expresan por unidad de longitud. El segundo término en 100 expresa la inductancia de fuga “en zigzag” resultante de armónicos en el orden de paso de ranura del rotor.

A continuación, vea que el flujo de la armadura es igual al flujo de entrehierro más la inductancia de fuga de armadura. Es decir, 68 podría escribirse como:

\[\ \underline{\Lambda}_{a}=\underline{\Lambda}_{a g}+L_{a l} \underline{I}_{a}\label{102} \]

Hay una serie de componentes de fugas en la ranura del estator\(\ L_{a l}\), cada uno de los cuales representa trayectorias de flujo que no involucran directamente al rotor. Cada uno de los componentes se suma a la inductancia de fuga. Los componentes más destacados de la fuga del estator se conocen como ranura, correa, zigzag, devanado final y sesgo. Cada uno de estos se discutirá en los siguientes párrafos.

Los componentes de fugas de correa y zigzag se deben a los armónicos de espacio de entrehierro. Resulta que estos son relativamente complicados de estimar, pero podemos obtener alguna noción de nuestra vista de primer orden de la máquina. El problema de estimar estos componentes de fuga es que no son realmente independientes del rotor, a pesar de que los llamamos “fuga”. Los armónicos de cinturón son de orden\(\ n=5\) y\(\ n=7\). Si no hubiera acoplamiento del rotor, los términos de fuga armónica de la correa serían:

\[\ X_{a g 5}=\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} N_{S}^{2} k_{5}^{2} R l}{5^{2} p^{2} g}\label{103} \]

\[\ X_{a g 7}=\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} N_{S}^{2} k_{7}^{2} R l}{7^{2} p^{2} g}\label{104} \]

Sin embargo, los armónicos de la correa se unen al rotor y en realidad parecen estar en paralelo con componentes de impedancia del rotor apropiados para máquinas de pares de polos de 5p y 7p. En estos órdenes armónicos generalmente podemos ignorar la resistencia del rotor para que la impedancia del rotor sea puramente inductiva. Esos componentes son:

\[\ X_{2,5}=\omega \frac{12 l N_{S}^{2} k_{5}^{2}}{N_{R}} L_{\mathrm{slot}}+\omega \frac{6}{\pi} \frac{\mu_{0} R l N_{S}^{2} k_{5}^{2}}{g}\left(\frac{1}{\left(N_{R}+5 p\right)^{2}}+\frac{1}{\left(N_{R}-5 p\right)^{2}}\right)\label{105} \]

\[\ X_{2,7}=\omega \frac{12 l N_{S}^{2} k_{7}^{2}}{N_{R}} L_{\mathrm{slot}}+\omega \frac{6}{\pi} \frac{\mu_{0} R l N_{S}^{2} k_{7}^{2}}{g}\left(\frac{1}{\left(N_{R}+7 p\right)^{2}}+\frac{1}{\left(N_{R}-7 p\right)^{2}}\right)\label{106} \]

En el modelo simple de la máquina de jaula de ardilla, debido a que las resistencias del rotor son relativamente pequeñas y se deslizan altas, generalmente se ignora el efecto de la resistencia del rotor. Luego, los componentes armónicos quinto y séptimo de la fuga de la correa son:

\[\ X_{5}=X_{a g 5} \| X_{2,5}\label{107} \]

\[\ X_{7}=X_{a g 7} \| X_{2,7}\label{108} \]

La fuga en zigzag del estator es de aquellos armónicos de las órdenes\(\ p n_{s}=N_{s l o t s} \pm p\) donde\(\ N_{\text {slots }}\).

\[\ X_{z}=\frac{3}{2} \frac{4}{\pi} \frac{\mu_{0} N_{S}^{2} R l}{g}\left(\frac{k_{n_{s}+}}{\left(N_{\text {slots }}+p\right)^{2}}+\frac{k_{n_{s}-}}{\left(N_{\text {slots }}-p\right)^{2}}\right)\label{109} \]

Tenga en cuenta que estos órdenes armónicos no tienden a ser cortocircuitados por la jaula del rotor y por lo tanto, normalmente no se tiene en cuenta ninguna interacción directa con la jaula.

Para reducir los efectos de prominencia que ocurren debido a que los dientes del rotor tenderán a intentar alinearse con los dientes del estator, los diseñadores de motores de inducción siempre utilizan un número diferente de ranuras en el rotor y el estator. Todavía puede haber cierta tendencia a alinearse, y esto produce pares “dentados” que a su vez producen vibraciones y ruido y, en casos severos, pueden retardar o incluso impedir el arranque. Para reducir esta tendencia al “diente”, los rotores a menudo se construyen con un poco de “sesgo”, o torsión de las ranuras de un extremo a otro. Así, cuando un diente está alineado en un extremo de la máquina, se desalinea en el otro extremo. Un efecto secundario de esto es reducir el acoplamiento del estator y el rotor en un poco, y esto produce reactancia de fuga. Esto es bastante fácil de estimar. Considere, por ejemplo, una densidad de flujo espacio-fundamental\(\ B_{r}=B_{1} \cos p \theta\), que enlaza una (posiblemente) trayectoria de corriente de paso completo sesgada:

\(\ \lambda=\int_{-\frac{l}{2}}^{\frac{l}{2}} \int_{-\frac{\pi}{2 p}+\frac{\varsigma}{p} \frac{x}{l}}^{\frac{\pi}{2 p}+\frac{\varsigma}{p} \frac{x}{l}} B_{1} \cos p \theta R d \theta d x\)

Aquí, el sesgo en el rotor son radianes\(\ \varsigma\) eléctricos de un extremo de la máquina al otro. Evaluación de estos rendimientos:

\(\ \lambda=\frac{2 B_{1} R l}{p} \frac{\sin \frac{\varsigma}{2}}{\frac{\varsigma}{2}}\)

Ahora bien, la diferencia entre lo que habría sido vinculado por un rotor no sesgado y lo que está vinculado por el rotor sesgado es el flujo de fuga sesgado, ahora expresable como:

\(\ X_{k}=X_{a g}\left(1-\frac{\sin \frac{\varsigma}{2}}{\frac{\varsigma}{2}}\right)\)

El componente final de la reactancia de fuga se debe a los devanados finales. Este es quizás el más difícil de los parámetros de la máquina de estimar, siendo esencialmente de naturaleza tridimensional. Hay varias formas de estimar este parámetro, pero para nuestros propósitos usaremos un parámetro simplificado de AlgerEquation\ ref {1}:

\(\ X_{e}=\frac{14}{4 \pi^{2}} \frac{q}{2} \frac{\mu_{0} R N_{a}^{2}}{p^{2}}(p-0.3)\)

Al igual que con todas esas fórmulas, aquí se requiere un cuidado extremo, ya que podemos dar poca orientación en cuanto a cuándo esta expresión es correcta o incluso cercana. Y admitiremos que un tratamiento más completo de este elemento de construcción de parámetros de máquina sería una mejora.

Resistencia del rotor de orden armónico y pérdidas de carga parásita

Es importante reconocer que el rotor de la máquina “ve” cada uno de los armónicos del estator esencialmente de la misma manera, y es bastante sencillo estimar los parámetros del rotor para los órdenes armónicos, como hemos hecho justo arriba. Ahora, particularmente para los órdenes armónicos de “correa”, hay corrientes de rotor que fluyen en respuesta a los mmf del estator en el quinto y séptimo orden armónico espacial. Las resistencias atribuibles a estos órdenes armónicos son:

\[\ R_{2,5}=\frac{12 l N_{s}^{2} k_{5}^{2}}{N_{R}} R_{\operatorname{slot}, 5}\label{110} \]

\[\ R_{2,7}=\frac{12 l N_{s}^{2} k_{7}^{2}}{N_{R}} R_{\mathrm{slot}, 7}\label{111} \]

Los armónicos de ranura de orden superior tendrán frecuencias relativas (resbalones) que son:

\ [\ s_ {n} =1\ mp (1-s) n\ left\ {\ begin {array} {l}
n=6 k+1\\
n=6 k-1
\ end {array}\ right\}\ mathrm {k}\ text {un entero}\ etiqueta {112}\]

La interacción electromagnética del motor de inducción puede describirse ahora mediante un circuito magnético aumentado como se muestra en la Figura 17. Tenga en cuenta que el flujo terminal de la máquina es la suma de todos los flujos armónicos, y cada armónico espacial es excitado por la misma corriente por lo que los componentes armónicos individuales están en serie.

Cada uno de los armónicos espaciales tendrá una interacción electromagnética similar a la fundamental: la potencia transferida a través del entrehierro es:

\(\ P_{e m, n}=3 I_{2, n}^{2} \frac{R_{2, n}}{s_{n}}\)

Por supuesto, la disipación en cada circuito es:

\(\ P_{d, n}=3 I_{2, n}^{2} R_{2, n}\)

dejando

\(\ P_{m, n}=3 I_{2, n}^{2} \frac{R_{2, n}}{s_{n}}\left(1-s_{n}\right)\)

Tenga en cuenta que este circuito equivalente tiene provisiones para dos conjuntos de circuitos que parecen “jaulas”. De hecho uno de estos conjuntos es para el cuerpo sólido del rotor si eso existe. Discutiremos eso anon. También hay una provisión\(\ \left(r_{c}\right)\) para la pérdida en el hierro del núcleo del estator.

La potencia depositada en los elementos de resistencia armónica del rotor se caracteriza como pérdida de “carga parásita” porque no se calcula fácilmente a partir del circuito equivalente de la máquina simple.

Modelos de Ranura

Algunas de las cosas más interesantes que se pueden hacer con los motores de inducción tienen que ver con la conformación de las ranuras del rotor para lograr efectos particulares dependientes de la frecuencia. Consideraremos aquí tres casos, pero hay muchas otras posibilidades.

Primero, supongamos que las ranuras del rotor son representables como rectangulares, como se muestra en la Figura 5, y supongamos que las dimensiones de las ranuras son tales que los efectos de difusión no son importantes de manera que la corriente en el conductor de ranura es aproximadamente uniforme. En ese caso, la resistencia de ranura y la inductancia por unidad de longitud son:

\[\ R_{\mathrm{slot}}=\frac{1}{w_{s} h_{s} \sigma}\label{113} \]

\[\ L_{\mathrm{slot}}=\mu_{0} \frac{h_{s}}{3 w_{s}}\label{114} \]

La resistencia de ranura es obvia, la inductancia de ranura puede estimarse reconociendo que si la corriente en la ranura es uniforme, el campo magnético que cruza la ranura debe ser:

\(\ H_{y}=\frac{I}{w_{s}} \frac{x}{h_{s}}\)

Entonces la energía almacenada en el campo en la ranura es simplemente:

\(\ \frac{1}{2} L_{\mathrm{slot}} I^{2}=w_{s} \int_{0}^{h_{s}} \frac{\mu_{0}}{2}\left(\frac{I x}{w_{s} h_{s}}\right)^{2} d x=\frac{1}{6} \frac{\mu_{0} h_{s}}{w_{s}} I^{2}\)

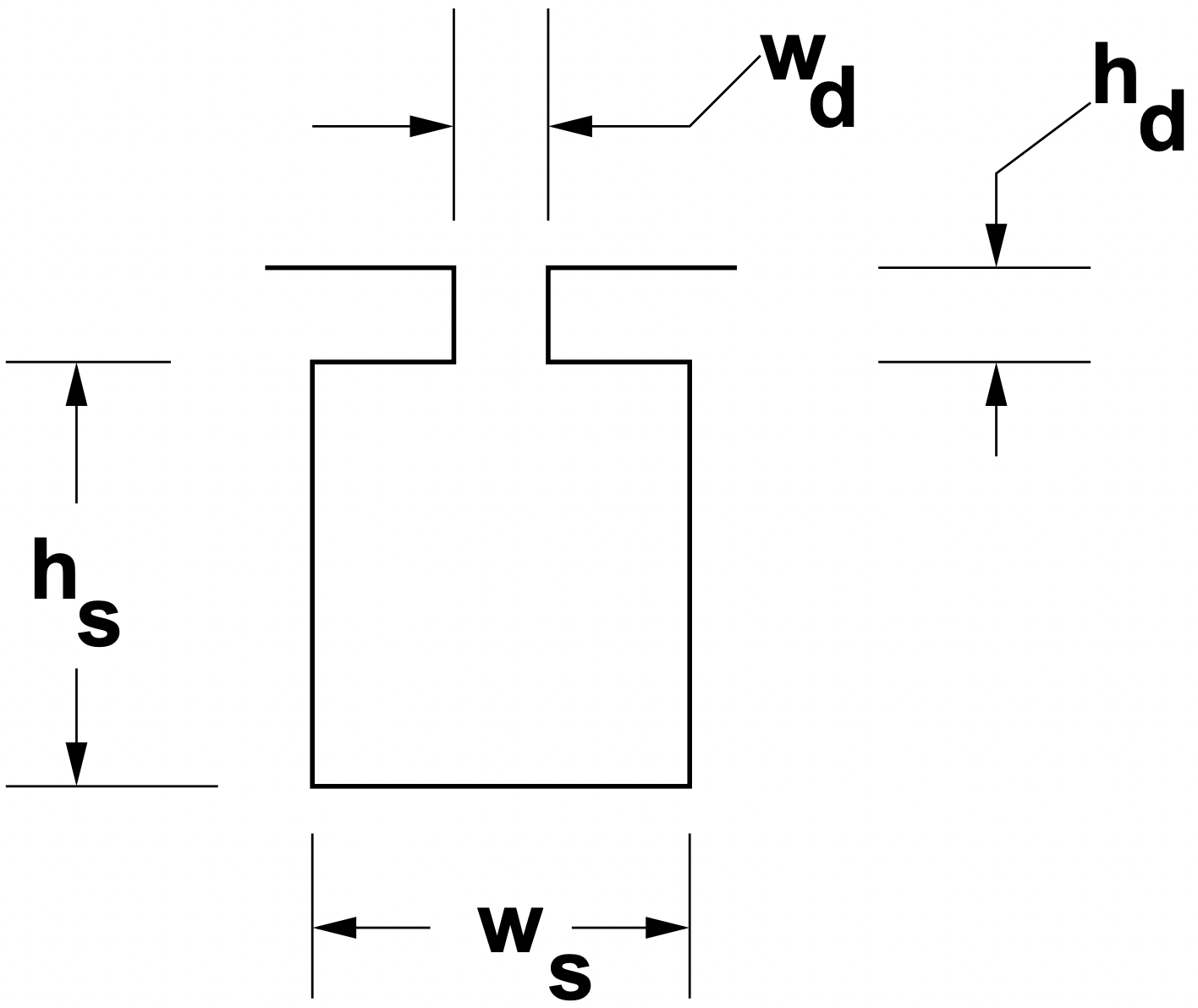Figura 5: Ranura única

Ranuras Profundas

Ahora, supongamos que la ranura no es lo suficientemente pequeña como para que se puedan ignorar los efectos de difusión. La ranura se vuelve “profunda” en la medida en que su profundidad es menor que (o incluso comparable a) la profundidad de la piel para la conducción a la frecuencia de deslizamiento. La conducción en este caso puede representarse usando la Ecuación de Difusión:

\(\ \nabla^{2} \bar{H}=\mu_{0} \sigma \frac{\partial \bar{H}}{\partial t}\)

En el estado estacionario, y suponiendo que solo el flujo de ranura cruzada (en la dirección y) es importante, y la única variación que es importante es en la dirección radial (x):

\(\ \frac{\partial^{2} H_{y}}{\partial x^{2}}=j \omega_{s} \mu_{0} \sigma H_{y}\)

Esto se resuelve mediante soluciones de la forma:

\(\ H_{y}=H_{\pm} e^{\pm(1+j) \frac{x}{\delta}}\)

donde la profundidad de la piel es

\(\ \delta=\sqrt{\frac{2}{\omega_{s} \mu_{0} \sigma}}\)

Dado que\(\ H_{y}\) debe desaparecer en la parte inferior de la ranura, debe tomar la forma:

\(\ H_{y}=H_{\operatorname{top}} \frac{\sinh (1+j) \frac{x}{\delta}}{\sinh (1+j) \frac{h_{s}}{\delta}}\)

Dado que la corriente es el rizo del campo magnético,

\(\ J_{z}=\sigma E_{z}=\frac{\partial H_{y}}{\partial x}=H_{\mathrm{top}} \frac{1+j}{\delta} \frac{\cosh (1+j) \frac{h_{s}}{\delta}}{\sinh (1+j) \frac{h_{s}}{\delta}}\)

Entonces la impedancia de ranura, por unidad de longitud, es:

\(\ Z_{\text {slot }}=\frac{1}{w_{s}} \frac{1+j}{\sigma \delta} \operatorname{coth}(1+j) \frac{h_{s}}{\delta}\)

Por supuesto, se debe agregar a esto la impedancia (puramente reactiva) debida a la depresión de la ranura. Es posible extraer las partes reales e imaginarias de esta impedancia (el proceso es algebraicamente un poco desordenado) para producir:

\ (\\ comenzar {alineado}
R_ {\ texto {ranura}} &=\ frac {1} {w_ {s}\ sigma\ delta}\ frac {\ sinh 2\ frac {h_ {s}} {\ delta} +\ sin 2\ frac {h_ {s}} {\ delta}} {\ cosh 2\ frac {h_ {s}} {delta} -\ cos 2\ frac {h_ {s}} {\ delta}}\\
L_ {\ text {slot}} &=\ mu_ {0}\ frac {h_ {d}} {w_ {d}} +\ frac {1} {\ omega_ {s}}\ frac {1} {w_ { s}\ sigma\ delta}\ frac {\ sinh 2\ frac {h_ {s}} {\ delta} -\ sin 2\ frac {h_ {s}} {\ delta}} {\ cosh 2\ frac {h_ {s}} {\ delta} -\ cos 2\ frac {h_ {s}} {\ delta}}
\ end {alineado}\)

Jaulas Múltiples

El propósito de una ranura “profunda” es mejorar el rendimiento de arranque de un motor. Cuando el rotor está estacionario, la frecuencia vista por los conductores del rotor es relativamente alta, y el hacinamiento de corriente debido al efecto de la piel hace que la resistencia del rotor parezca ser alta. A medida que el rotor acelera la frecuencia vista desde las caídas del rotor, disminuyendo el efecto de la piel y haciendo más uso del conductor del rotor. Esto, entonces, le da a la máquina un mayor par de arranque (que requiere alta resistencia) sin comprometer la eficiencia de funcionamiento.

Este efecto se puede llevar aún más haciendo uso de múltiples jaulas, tal como se muestra en la Figura 6. Aquí hay dos conductores en una ranura bastante compleja. La estimación de la impedancia de esta ranura se realiza en etapas para construir un circuito equivalente.

Supongamos a los efectos de esta derivación que cada sección de la jaula múltiple es lo suficientemente pequeña como para que las corrientes puedan considerarse uniformes en cada conductor. Entonces la sección inferior puede representarse como una resistencia en serie con una inductancia:

\(\ R_{a}=\frac{1}{\sigma w_{1} h_{1}}\)

\(\ L_{a}=\frac{\mu_{0}}{3} \frac{h_{1}}{w_{1}}\)

La sección de ranura estrecha sin conductor entre los conductores superior e inferior contribuirá con una impedancia inductiva:

\(\ L_{s}=\mu_{0} \frac{h_{s}}{w_{s}}\)

El conductor superior tendrá una resistencia:

\(\ R_{b}=\frac{1}{\sigma w_{2} h_{2}}\)

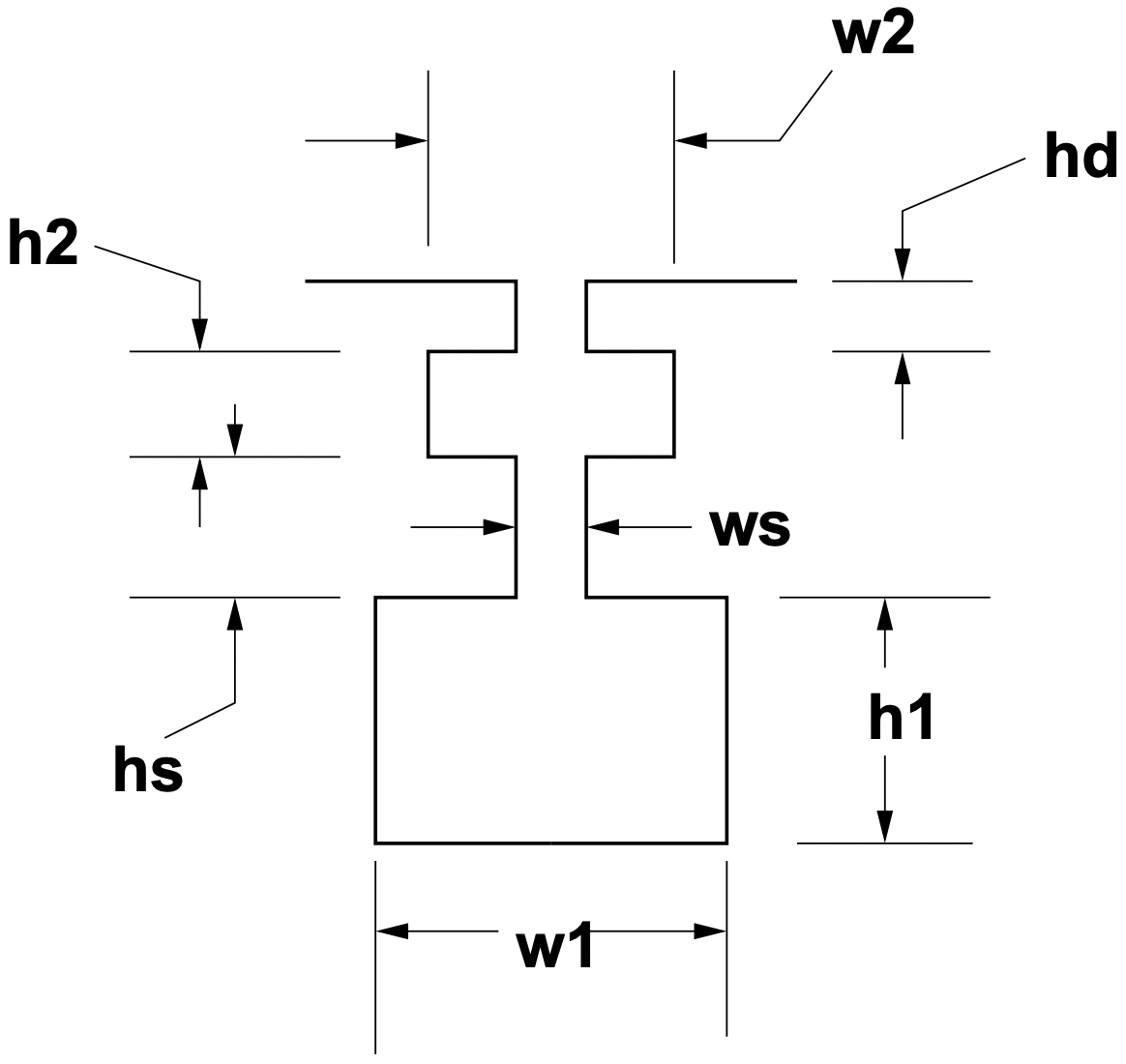Figura 6: Ranura Doble

Ahora, en el circuito equivalente, la corriente que fluye en el conductor inferior producirá un campo magnético a través de esta sección, produciendo una inductancia en serie de

\(\ L_{b}=\mu_{0} \frac{h_{2}}{w_{2}}\)

Por analogía con el conductor inferior, la corriente en el conductor superior fluye a través de solo un tercio de la inductancia de la sección superior, conduciendo al circuito equivalente de la Figura 7, una vez que se agrega la inductancia de la depresión de la ranura en:

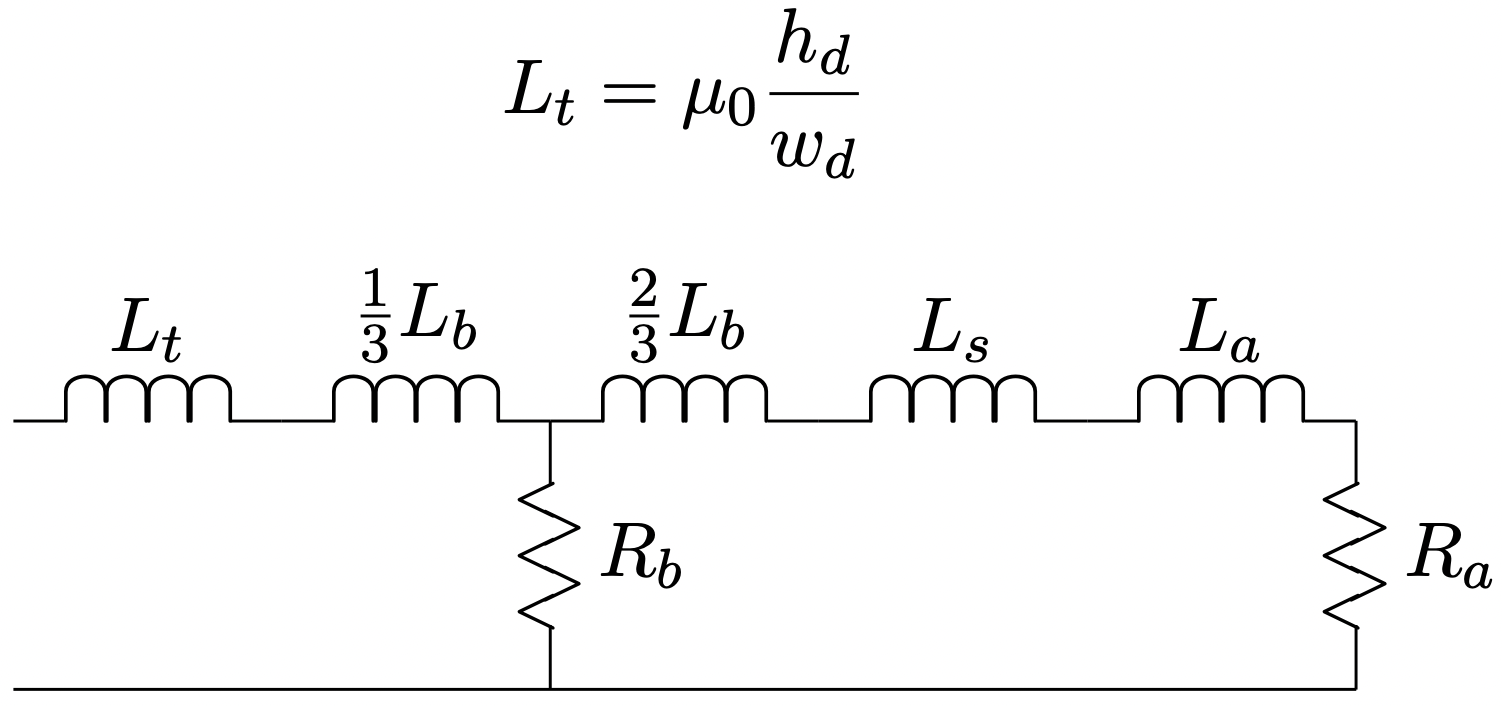Figura 7: Circuito Equivalente: Doble Barra

Ahora, este circuito de barra de rotor encaja directamente en el marco del circuito equivalente del motor de inducción, mostrado para la caja de doble jaula en la Figura 8, con

\ (\\ comenzar {alineado}
R_ {2 a} &=\ frac {12 l N_ {S} ^ {2} k_ {S} ^ {2}} {N_ {R}} R_ {a}\\
R_ {2 b} &=\ frac {12 l N_ {S} ^ {2} k_ {S} ^ {2}} {N_ {R}} R_ {b}
\ final {alineado}\)

\ (\\ comenzar {alineado}
X_ {2 a} &=\ omega\ frac {12 l N_ {S} ^ {2} k_ {S} ^ {2}} {N_ {R}}\ izquierda (\ frac {2} {3} L_ {b} +L_ {s} +L_ {a}\ derecha)\\
X_ {2 a} &=\ omega\ frac {12 l N_ {S} ^ {2} k_ {S} ^ {2}} {N_ {R}}\ izquierda (L_ {t} +\ frac {1} {3} L_ {b}\ derecha)
\ final {alineado}\)

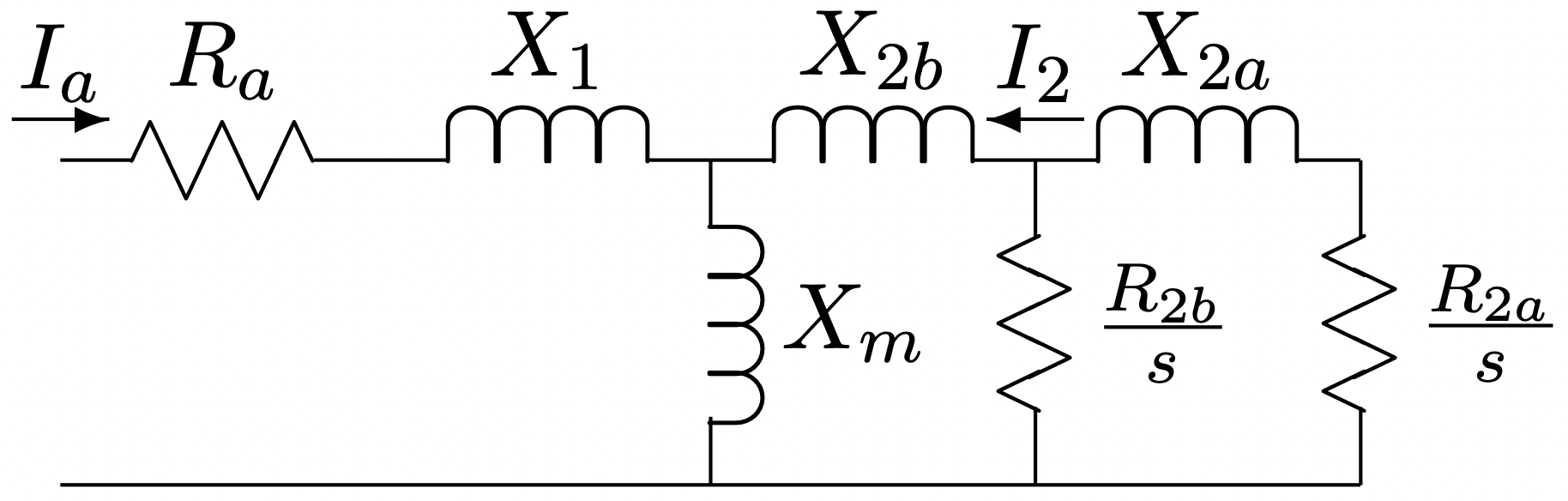Figura 8: Circuito equivalente: Rotor de doble jaula

Efectos del anillo final del rotor

Es necesario corregir la resistencia del “anillo final” en el rotor. Para ello, observamos que la magnitud de la densidad de corriente superficial en el rotor está relacionada con la magnitud de la corriente de barra individual por:

\(\ I_{z}=K_{z} \frac{2 \pi R}{N_{R}}\label{115}\)

La corriente en el anillo final es:

\(\ I_{R}=K_{z} \frac{R}{p}\label{116}\)

Entonces es sencillo calcular la relación entre la potencia disipada en los anillos extremos y la potencia disipada en las propias barras conductoras, considerando la relación de densidades y volúmenes de corriente. Suponiendo que las barras y los anillos extremos tienen la misma extensión radial, la relación de densidades de corriente es:

\(\ \frac{J_{R}}{J_{z}}=\frac{N_{R}}{2 \pi p} \frac{w_{r}}{l_{r}}\label{117}\)

donde\(\ w_{r}\) es el ancho promedio de una barra conductora y\(\ l_{r}\) es la longitud del anillo extremo axial.

Ahora, la relación de pérdidas (y de ahí la relación de resistencias) se encuentra multiplicando el cuadrado de la relación de densidad de corriente por la relación de volúmenes. Esto es aproximadamente:

\[\ \frac{R_{\text {end }}}{R_{\text {slot }}}=\left(\frac{N_{R}}{2 \pi p} \frac{w_{r}}{l_{r}}\right)^{2} 2 \frac{2 \pi R}{N_{R} l} \frac{l_{r}}{w_{r}}=\frac{N_{R} R w_{r}}{\pi l l_{r} p^{2}}\label{118} \]

Windage

La fricción de los rodamientos, la pérdida de viento y la potencia de entrada del ventilador a menudo se consideran elementos de un “arte negro”. Nos acercamos a ellos con cierto nivel de inquietud, ya que los fabricantes de motores parecen tener una visión altamente empírica de estos elementos. Lo que sigue es un intento de construir modelos razonables pero simples para dos efectos: pérdida en el entrehierro debido al viento y potencia de entrada al ventilador para enfriamiento. Aquí se requiere cierta precaución, ya que estos elementos de cálculo no han sido probados adecuadamente, aunque parecen dar números razonables

El primer elemento es la pérdida por viento de brecha. Esto se produce por cizallamiento del aire en el espacio de rotación relativo. Es probable que sea un elemento significativo solo en máquinas con brechas de aire muy estrechas o velocidades superficiales muy altas. Pero estas incluyen, por supuesto, las máquinas de alto rendimiento con las que más nos interesa. Abordamos esto con un sencillo modelo de “couette flow”. La pérdida por cizallamiento del entrehierro es aproximadamente:

\[\ P_{w}=2 \pi R^{4} \Omega^{3} l \rho_{a} f\label{119} \]

donde\(\ \rho_{a}\) es la densidad del medio de entrehierro (posiblemente aire) y\(\ f\) es el factor de fricción, estimado por:

\[\ f=\frac{.0076}{R_{n}^{\frac{1}{4}}}\label{120} \]

y el número de Reynold\(\ R_{n}\) es

\[\ R_{n}=\frac{\Omega R g}{\nu_{\text {air }}}\label{121} \]

y\(\ \nu_{\text {air }}\) es la viscosidad cinemática del medio de entrehierro.

El segundo elemento es la potencia de entrada del ventilador. Basamos una estimación de esto en dos hipótesis. El primero de ellos es que el flujo másico de aire que circula por el ventilador se puede calcular por la pérdida en el motor y un aumento de temperatura promedio en el aire de refrigeración. La segunda hipótesis es que el aumento de presión del ventilador se establece por el aumento de presión centrífuga asociado con la velocidad superficial en el exterior del rotor. Tomando estos uno a la vez: Si va a haber un aumento de temperatura\(\ \Delta T\) en el aire de enfriamiento, entonces el volumen de flujo másico es:

\(\ \dot{m}=\frac{P_{d}}{C_{p} \Delta T}\)

y luego el flujo volumétrico es solo

\(\ \dot{v}=\frac{\dot{m}}{\rho_{\text {air }}}\)

El aumento de presión se estima por la fuerza centrífuga:

\(\ \Delta P=\rho_{\text {air }}\left(\frac{\omega}{p} r_{\mathrm{fan}}\right)^{2}\)

entonces el poder viene dado por:

\(\ P_{\text {fan }}=\Delta P \dot{v}\)

Como referencia, las propiedades del aire son:

Densidad	\(\ \rho_{\text {air }}\)	1.18	\(\ \mathrm{kg} / \mathrm{m}^{2}\)
Viscosidad Cinemática	\\ nu_ {\ texto {aire}}	\(\ 1.56 \times 10^{-5}\)	\(\ m^{2} / s e c\)
Capacidad de Calor	\(\ C_{p}\)	1005.7	\(\ \mathrm{J} / \mathrm{kg}\)

Pérdida y excitación del circuito magnético

Habrá alguna pérdida en el circuito magnético del estator debido a la corriente parásita y los efectos de histéresis en el núcleo de hierro. Además, particularmente si los dientes del rotor y del estator están saturados, habrá MMF gastados para empujar el flujo a través de esas regiones. Estos efectos son muy difíciles de estimar a partir de los primeros principios, por lo que recurrimos a un modelo sencillo.

Supongamos que la pérdida en acero saturado sigue una ley como:

\[\ P_{d}=P_{B}\left(\frac{\omega_{e}}{\omega_{B}}\right)^{\epsilon_{f}}\left(\frac{B}{B_{B}}\right)^{\epsilon_{b}}\label{122} \]

Esto no es tan malo una estimación para el comportamiento del núcleo de hierro. Típicamente,\(\ \epsilon_{f}\) es un poco menor que dos (entre aproximadamente 1.3 y 1.6) y\(\ \epsilon_{b}\) es un poco más de dos (entre aproximadamente 2.1 y 2.4). Por supuesto, este modelo es bueno solo para un rango bastante restringido de densidad de flujo. La disipación de base generalmente se expresa en “vatios por kilogramo”, por lo que primero calculamos la densidad de flujo y luego la masa de los dos componentes principales del hierro del estator, los dientes y el hierro posterior.

De manera similar podemos modelar los emocionantes volt-amperios consumidos por el núcleo de hierro por algo así como:

\[\ Q_{c}=\left(V a_{1}\left(\frac{B}{B_{B}}\right)^{\epsilon_{v 1}}+V a_{2}\left(\frac{B}{B_{B}}\right)^{\epsilon_{v 2}}\right) \frac{\omega}{\omega_{B}}\label{123} \]

Esta, también, es una forma que parece ser válida para algunos aceros. Obviamente, puede ser necesario desarrollar diferentes formas de 'ajustes' de curva para diferentes materiales.

La densidad de flujo (RMS) en el entrehierro es:

\[\ B\_{r}=\frac{p V_{a}}{2 R l N_{a} k_{1} \omega_{s}}\label{124} \]

Entonces la densidad de flujo en los dientes del estator es:

\[\ B_{t}=B_{r} \frac{w_{t}+w_{1}}{w_{t}}\label{125} \]

donde\(\ w_{t}\) es el ancho del diente y\(\ w_{1}\) es el ancho superior de la ranura. El flujo en el hierro posterior del núcleo es

\[\ B_{c}=B_{r} \frac{R}{p d_{c}}\label{126} \]

donde\(\ d_{c}\) está la profundidad radial del núcleo.

Una forma de manejar esta pérdida es asumir que el núcleo maneja el flujo correspondiente al voltaje del terminal, sumar las pérdidas y luego calcular una resistencia y reactancia equivalentes:

\ (\\ begin {array} {l}
r_ {c} =\ frac {3\ izquierda|v_ {a}\ derecha|^ {2}} {P_ {\ text {núcleo}}}\
x_ {c} =\ frac {3\ izquierda|v_ {a}\ derecha|^ {2}} {Q_ {\ text {núcleo}}
\ fin matriz}\)

luego poner esta resistencia equivalente en paralelo con el elemento de reactancia de entrehierro en el circuito equivalente.