10.5: Control de velocidad del motor de inducción
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introducción
Los atributos inherentes de las máquinas de inducción las hacen muy atractivas para aplicaciones de accionamiento. Son robustos, económicos de construir y no tienen contactos deslizantes que desgastar. La dificultad de usar máquinas de inducción en servomecanismos y variadores de velocidad es que son “difíciles de controlar”, ya que su relación par-velocidad es compleja y no lineal. Sin embargo, con la electrónica de potencia moderna para servir como cambiadores de frecuencia y electrónica digital para hacer la aritmética requerida, las máquinas de inducción están viendo un uso creciente en aplicaciones de accionamiento.
En este capítulo desarrollamos modelos para el control de motores de inducción. La derivación es bastante breve ya que se basa en lo que ya hemos hecho para las máquinas síncronas. En este capítulo, sin embargo, nos quedaremos en variables “ordinarias”, omitiendo la normalización por unidad.
Voltios/Hz Control
Recordando que las máquinas de inducción generalmente tienden a operar a un deslizamiento relativamente bajo por unidad, podríamos concluir que una forma de construir un accionamiento de velocidad ajustable sería suministrar un motor de inducción con frecuencia de estator ajustable. Y esto es, efectivamente, posible. Una cosa a recordar es que el flujo es inversamente proporcional a la frecuencia, por lo que para mantener el flujo constante se debe hacer que el voltaje del estator sea proporcional a la frecuencia (de ahí el nombre “voltes/Hz constantes”). Sin embargo, los suministros de voltaje son siempre limitados, por lo que a alguna frecuencia es necesario cambiar a control de voltaje constante. La analogía con las máquinas de CC es bastante directa aquí: por debajo de cierta velocidad “base”, la máquina se controla en modo de flujo constante (“voltios/Hz”), mientras que por encima de la velocidad base, el flujo es inversamente proporcional a la velocidad. Es fácil ver que el par máximo es entonces inversamente al cuadrado de flujo, o por lo tanto al cuadrado de frecuencia.
Para obtener una imagen de primer orden de cómo funciona una máquina de inducción a velocidad ajustable, comience con la red equivalente simplificada que describe la máquina, como se muestra en la Figura 9
Anteriormente en este capítulo, se demostró que el par puede calcularse encontrando la potencia disipada en la resistencia virtual R2/s y dividiendo por la velocidad eléctrica. Para una máquina trifásica, y suponiendo que estamos tratando con magnitudes RMS:
Te=3pω|I2|2R2s
donde ω está la frecuencia eléctrica y p es el número de pares de polos. Es sencillo de encontrar I2 usando técnicas de red. Como ejemplo, la Figura 10 muestra una serie de curvas de par/velocidad para
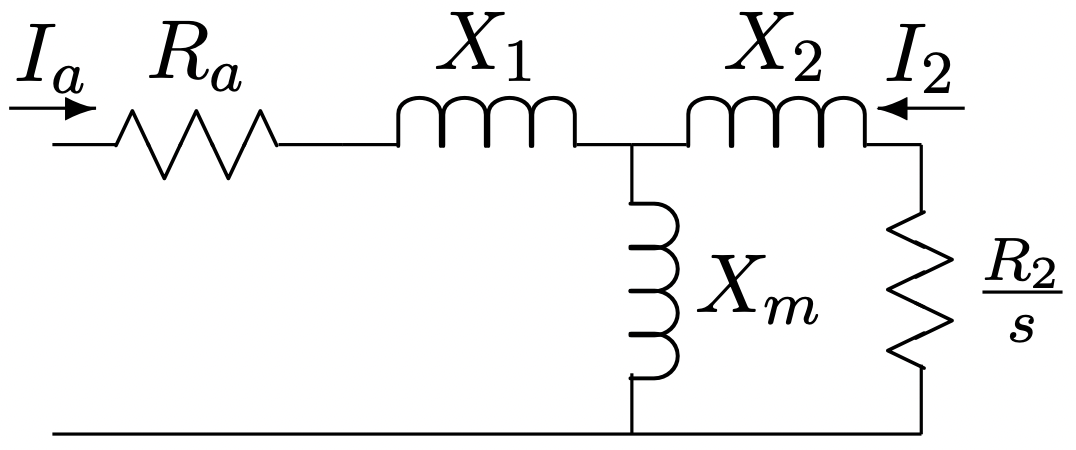 Figura 9: Circuito equivalente
Figura 9: Circuito equivalenteuna máquina de inducción operada con una amplia gama de frecuencias de entrada, tanto por debajo como por encima de su frecuencia “base”. Los parámetros de esta máquina son:
| Número de Fases | 3 |
| Número de pares de polos | 3 |
| Voltaje de terminal RMS (línea-línea) | 230 |
| Frecuencia (Hz) | 60 |
| Resistencia del estator R1 | .06 Ω |
| Resistencia del Rotor R2 | .055 Ω |
| Fuga del Estator X1 | .34 Ω |
| Fuga del Rotor X2 | .33 Ω |
| Reactancia de magnetización Xm | 10.6 Ω |
La estrategia para operar la máquina es hacer que la magnitud del voltaje del terminal sea proporcional a la frecuencia para frecuencias de entrada menores que la “Frecuencia Base”, en este caso 60 Hz, y mantener constante la tensión para frecuencias por encima de la “Frecuencia Base”.
Para frecuencias altas la producción de par cae bastante rápido con la frecuencia (como resulta, es aproximadamente proporcional a la inversa del cuadrado de frecuencia). También cae con muy baja frecuencia debido a los efectos de la resistencia terminal. Vamos a ver esto a continuación.
Modelo idealizado: sin resistencia del estator
Ignorar, por el momento, R1. Un circuito equivalente se muestra en la Figura 11. Es bastante fácil demostrar que, desde el rotor, la combinación de fuente, fuga de armadura y rama magnetizante puede ser reemplazada por su circuito equivalente, como se muestra en la Figura 12.
En el circuito de la Figura 12, los parámetros son:
\ (\\ begin {alineado}
V^ {\ prime} &=V\ frac {X_ {m}} {X_ {m} +X_ {1}}\\
X^ {\ prime} &=X_ {m}\ | X_ {1}
\ end {alineado}\)
Si la máquina funciona a frecuencia variable ω, pero la reactancia se establece en frecuencia ωB, la corriente es:
I_=V′j(X′1+X2)ωωB+R2s
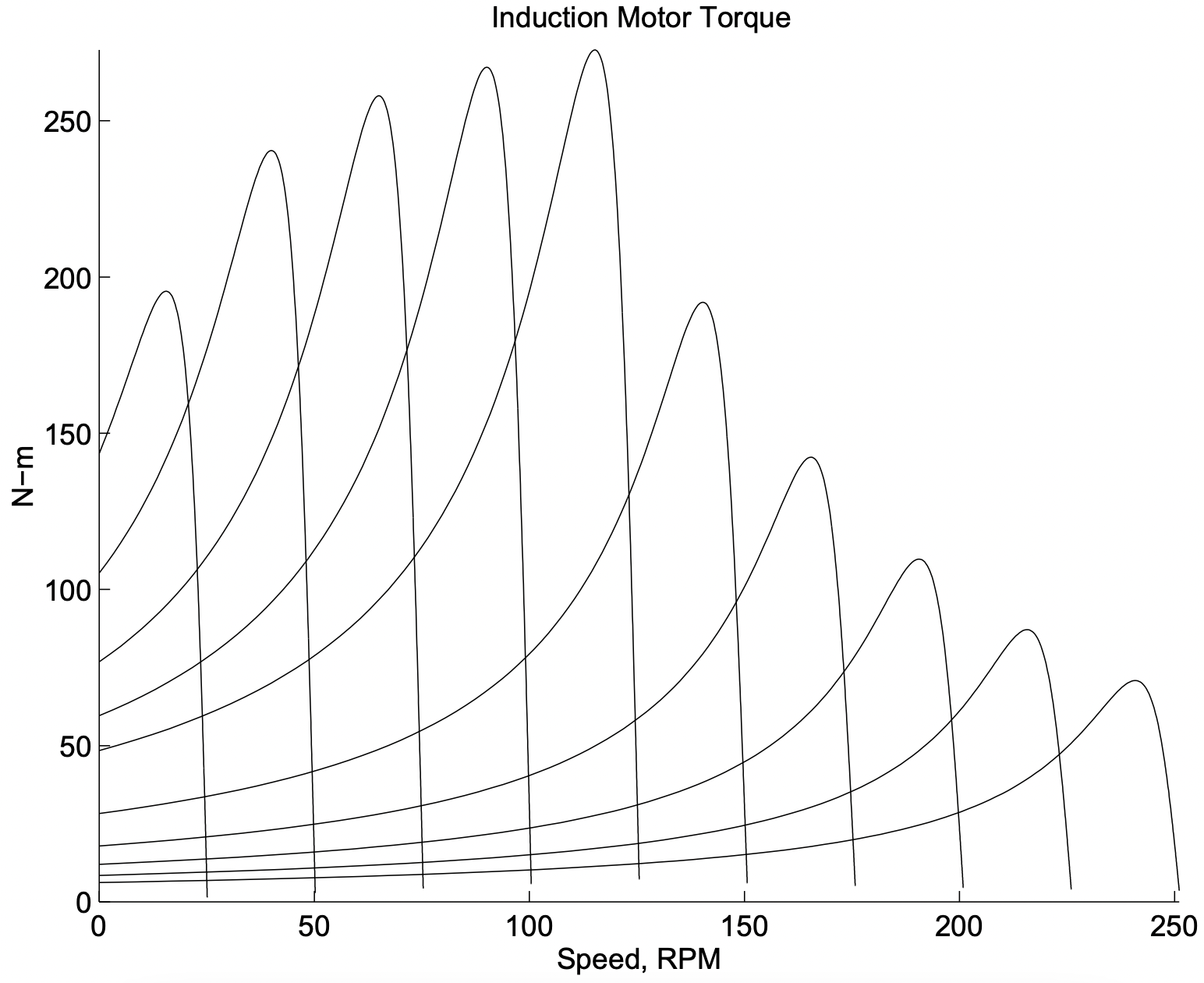 Figura 10: Curvas de Torque-Velocidad de Máquina de Inducción
Figura 10: Curvas de Torque-Velocidad de Máquina de Inducción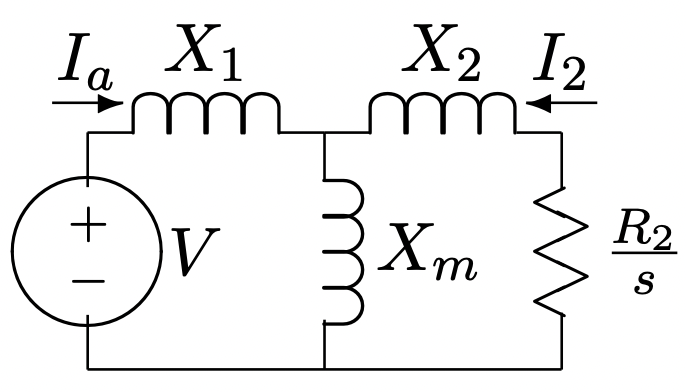 Figura 11: Circuito idealizado: Ignorar la resistencia de la armadura
Figura 11: Circuito idealizado: Ignorar la resistencia de la armaduray luego el par es
Te=3|I2|2R2s=3pω|V′|2R2s(X′1+X2)2+(R2s)2
Ahora bien, si observamos que lo que cuenta es el deslizamiento absoluto del rotor, podríamos definir un deslizamiento con respecto a la frecuencia base:
s=ωrω=ωrωBωBω=sBωBω
Entonces, si asumimos que el voltaje se aplica proporcional a la frecuencia:
V′=V′0ωωB
y con un poco de manipulación, obtenemos:
Te=3pωB|V′0|2R2sB(X′1+X2)2+(R2sB)2
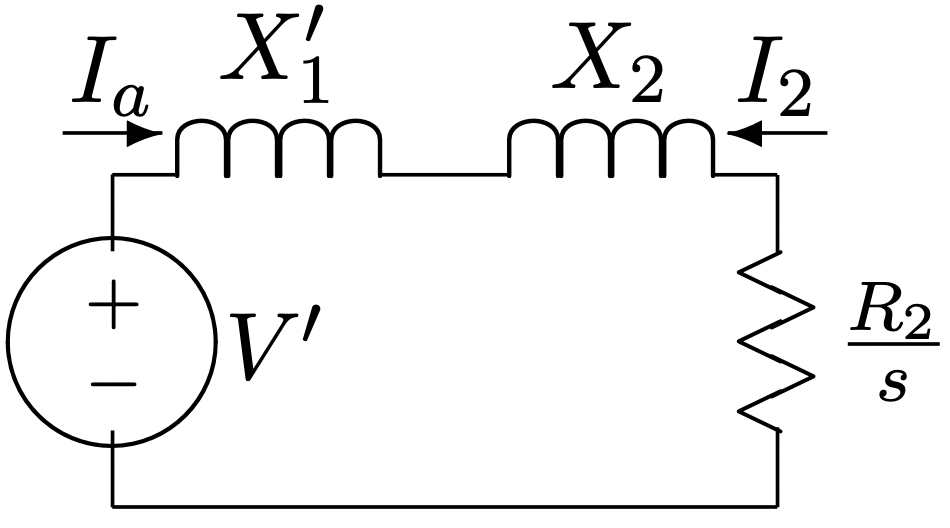 Figura 12: Equivalente idealizado
Figura 12: Equivalente idealizadoEsto implicaría que el par es, si el voltaje es proporcional a la frecuencia, es decir, flujo constante aplicado, dependiente solo del deslizamiento absoluto. La curva par-velocidad es una constante, dependiente solo de la diferencia entre la velocidad sincrónica y la real del rotor.
Esto está bien, pero finalmente, la noción de “voltios por Hz” se agota porque a algún número de Hz, no hay más voltios para tener. Esta generalmente se toma como la velocidad “base” para la unidad. Por encima de esa velocidad, el voltaje se mantiene constante y el par viene dado por:
Te=3pωB|V′|2R2sB(X′1+X2)2+(R2sB)2
El pico de este par tiene una dependencia cuadrada inversa de la frecuencia, como puede verse en la Figura 13.
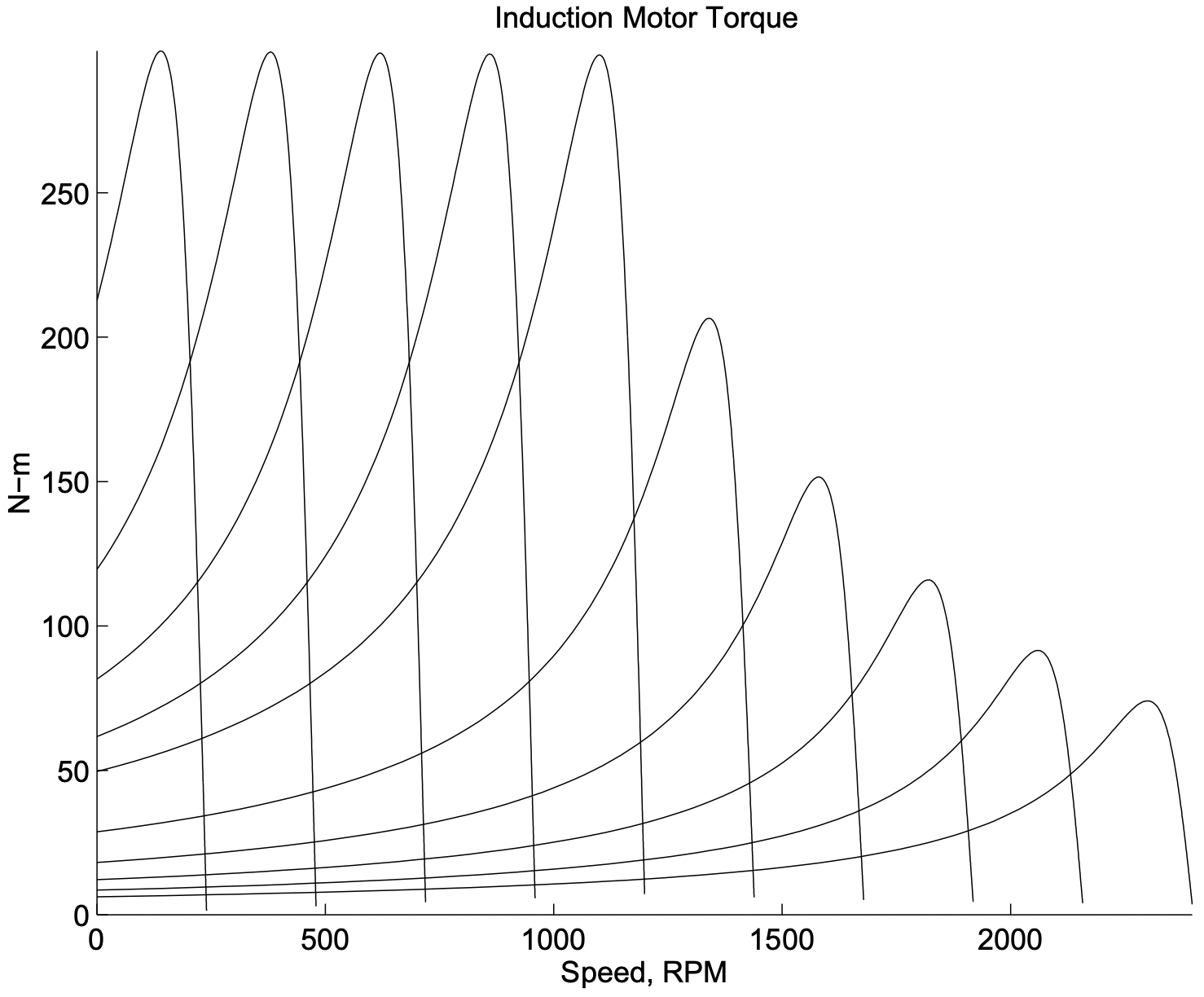 Figura 13: Curvas idealizadas de par-velocidad: Resistencia cero del estator
Figura 13: Curvas idealizadas de par-velocidad: Resistencia cero del estatorCapacidad de par máximo
Suponiendo que tenemos un controlador inteligente, estamos interesados en la capacidad real de la máquina. A cierta tensión y frecuencia, el par viene dado por:
Te=3|I2|2R2s=3pω|V′|2R2s((X′1+X2)(ωωB))2+(R′1+R2s)2
Ahora, nos interesa encontrar el valor pico de eso, que viene dado por el valor de R2s lo que maximiza la transferencia de potencia a la resistencia virtual. Esto viene dado por la condición coincidente:
R2s=√R′21+((X′1+X2)(ωωB))2
Entonces el par máximo (avería) viene dado por:
Tmax
Esto se representa en la Figura 14. Así como una comprobación, esto se calculó asumiendo\ R_{1}=0, y los resultados se trazan en la figura 15. Esta gráfica muestra, como cabría esperar, una región límite de par constante a velocidad cero.
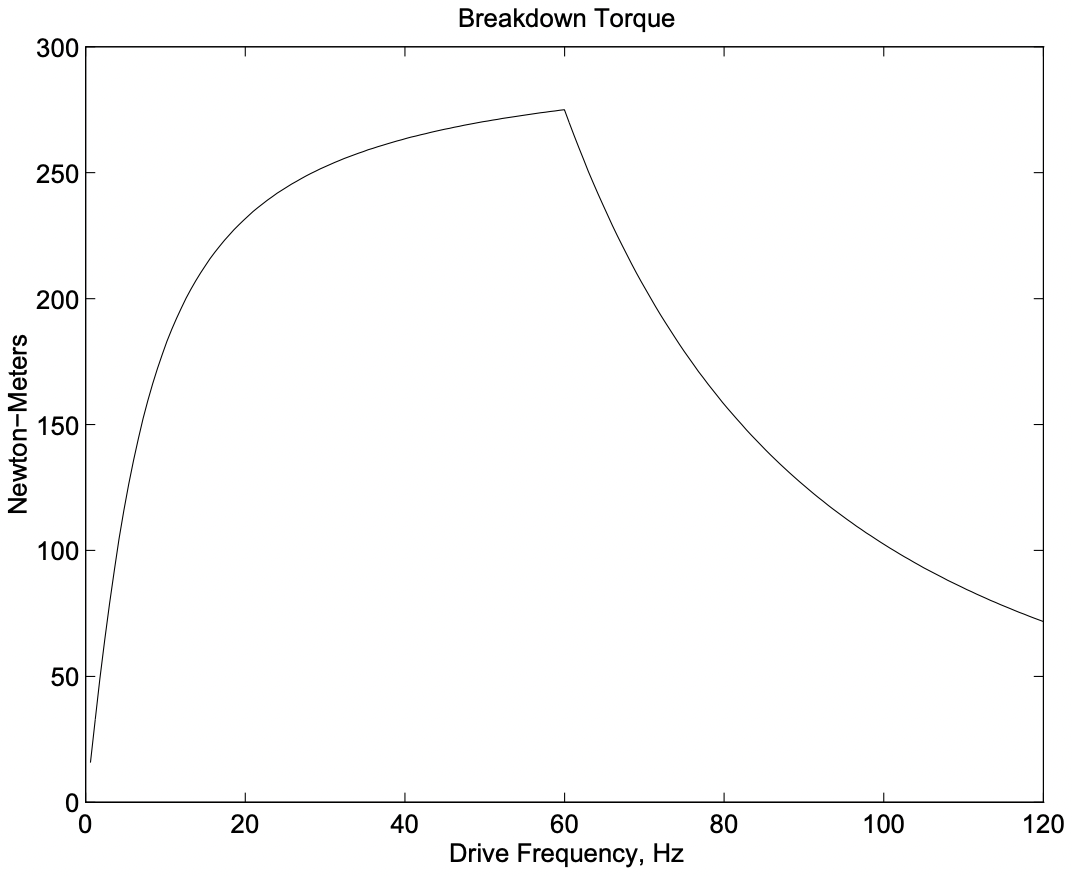 Figura 14: Curva de capacidad de par para un motor de inducción
Figura 14: Curva de capacidad de par para un motor de inducciónControl Orientado a Campo
Uno de los impactos más útiles de la electrónica de potencia moderna y la tecnología de control nos ha permitido convertir las máquinas de inducción en servomotores de alto rendimiento. En esta nota desarrollaremos un
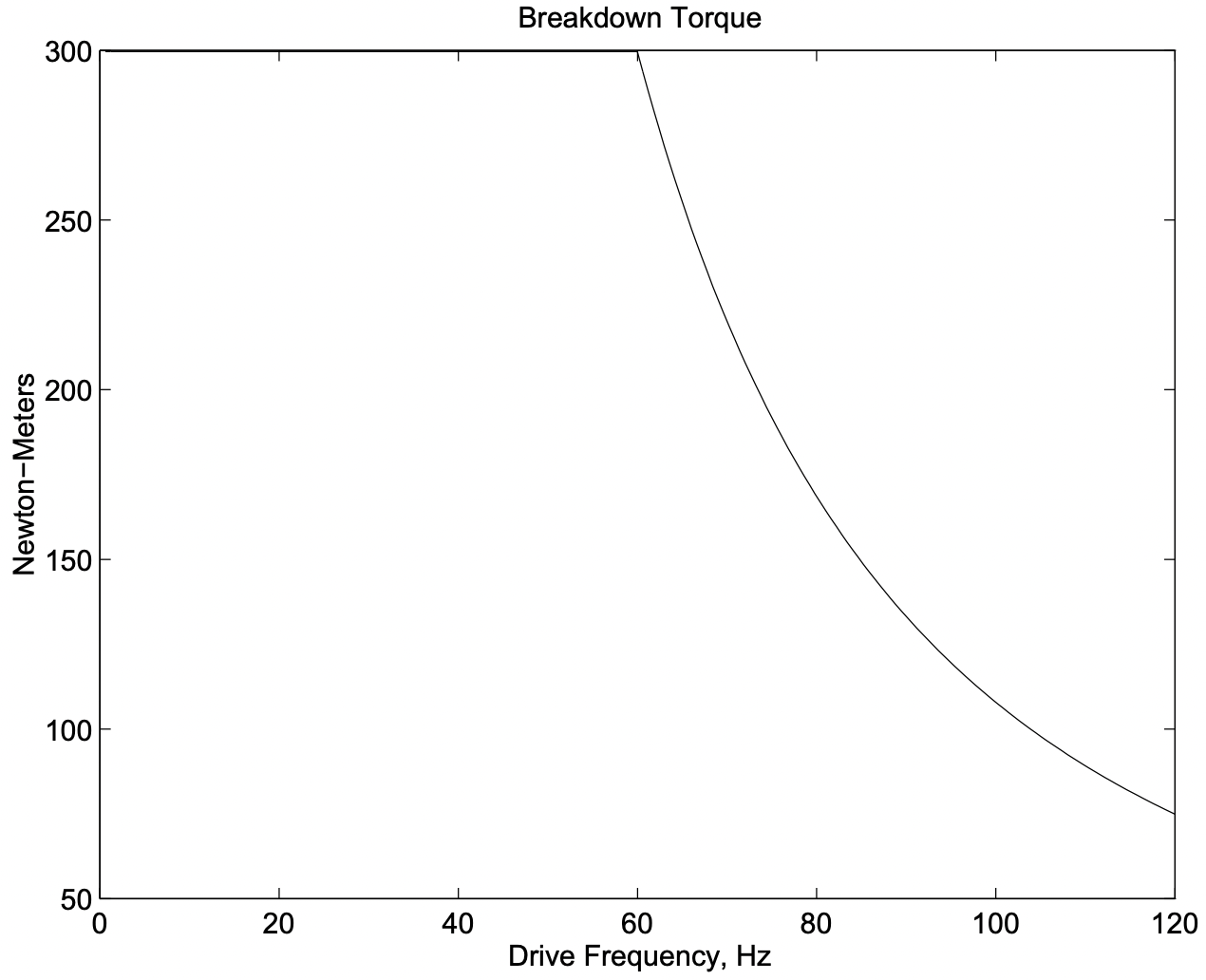 Figura 15: Curva de capacidad de par idealizado: Resistencia cero del estator
Figura 15: Curva de capacidad de par idealizado: Resistencia cero del estatorimagen de cómo se hace esto. Obviamente hay muchos detalles que no vamos a tocar aquí. El objetivo es emular el rendimiento de una máquina de CC, en la que (como recordará), el torque es una función simple de la corriente aplicada. Para una máquina con un devanado de campo, esto es simplemente:
\ T=G I_{f} I_{a}
Esto hace que el control de una máquina de este tipo sea bastante fácil, ya que una vez que se conoce el par deseado es fácil traducir ese comando de par en una corriente y el motor hace el resto.
Por supuesto, las máquinas de CC (colector) son, al menos en tamaños grandes, caras, no particularmente eficientes, tienen requisitos de mantenimiento relativamente altos debido a la interfaz de escobilla deslizante/colector, proporcionan problemas ambientales debido a chispas y polvo de carbono y son ambientalmente sensibles. El motor de inducción es más simple y resistente. Hasta hace bastante poco el motor de inducción no ha sido ampliamente utilizado en aplicaciones de servo porque se pensaba que era “difícil de controlar”. Como mostraremos, sí se necesita un poco de esfuerzo e incluso algunos cómputos para hacer bien los controles, pero esto se está volviendo cada vez más asequible.
Modelo Elemental
Volvemos al modelo elemental del motor de inducción. En las variables ordinarias, referidas al estator, la máquina se describe por relaciones flujo-corriente (en el marco de referencia d-q):
\ (\\ begin {aligned}
\ left [\ begin {array} {c}
\ lambda_ {d S}\
\ lambda_ {d R}
\ end {array}\ right] &=\ left [\ begin {array} {ll}
L_ {S} & M\
M & L_ {R}
\ end {array}\ right]\ left [\ begin {array} {c}
i_ {d S}\\
i_ {d R}
\ end {array}\ derecha]\
\\ izquierda [\ begin {array} {c}
\ lambda_ {q S}\
\ lambda_ {q R}
\ end {array}\ right] &=\ left [\ begin {array} {ll}
L_ {S} & M\
M & L_ {R}
\ end {array}\ right]\ left [\ begin {array} {c}
i_ {q S}\\
i_ {q R}
\ end {array}\ right]
\ end {alineada}\)
Tenga en cuenta que la máquina es simétrica (no hay prominencia), y como nos refieren al estator, las autoinductancias del estator y del rotor incluyen términos de fuga:
\ (\\ begin {array} {l}
L_ {S} =M+L_ {S\ ell}\\
L_ {R} =M+L_ {R\ ell}
\ end {array}\)
Las ecuaciones de voltaje son:
\ (\\ comenzar {alineado}
v_ {d S} &=\ frac {d\ lambda_ {d S}} {d t} -\ omega\ lambda_ {q S} +r_ {S} i_ {d S}\\
v_ {q S} &=\ frac {d\ lambda_ {q S}} {d t} +\ omega\ lambda_ d {S} +r_ {S} i_ {q S}\\
0 &=\ frac {d\ lambda_ {d R}} {d t} -\ omega_ {s}\ lambda_ {q R} +r_ {R} i_ {d R}\\
0 &=\ frac {d\ lambda_ {q R}} {d t} +\ omega_ {s}\ lambda_ {d R} +r_ {R} i_ {q R}
\ end {alineado}\)
Tenga en cuenta que tanto el rotor como el estator tienen términos de voltaje de “velocidad” ya que ambos están girando con respecto al sistema de coordenadas giratorias. La velocidad del sistema de coordenadas giratorias es w con respecto al estator. Con respecto al rotor esa velocidad es, donde wm es la velocidad mecánica del rotor. Tenga en cuenta que este análisis no requiere que la velocidad w del sistema de coordenadas del marco de referencia sea constante.
El par viene dado por:
\ T^{e}=\frac{3}{2} p\left(\lambda_{d S} i_{q S}-\lambda_{q S} i_{d S}\right)
Modelo de simulación
Como primer paso en el desarrollo de un modelo de simulación, vea que la inversión de la relación flujo-corriente es (utilizamos el eje d ya que el eje q es idéntico):
\ (\\ comenzar {alineado}
i_ {d S} &=\ frac {L_ {R}} {L_ {S} L_ {R} -M^ {2}}\ lambda_ {d S} -\ frac {M} {L_ {S} L_ {R} -M^ {2}}\ lambda_ {d R}\
i_ {d} &= frac {M} {L_ {S} L_ {R} -M^ {2}}\ lambda_ {d S} -\ frac {L_ {S}} {L_ {S} L_ {R} -M^ {2}}\ lambda_ {d R}
\ end {alineado}\)
Ahora bien, si hacemos las siguientes definiciones (la motivación para esto ya debería ser obvia):
\ (\\ comenzar {alineado}
X_ {d} &=\ omega_ {0} L_ {S}\\
X_ {k d} &=\ omega_ {0} L_ {R}\
X_ {a d} &=\ omega_ {0} M\\
X_ {d} ^ {\ prime} &=\ omega_ {0}\ izquierda (L_ {S} -\ frac {M^ {2}} {L_ {R}}\ derecha)
\ final {alineado}\)
las corrientes se convierten en:
\ (\\ begin {alineado}
i_ {d S} &=\ frac {\ omega_ {0}} {X_ {d} ^ {\ prime}}\ lambda_ {d S} -\ frac {X_ {a d}} {X_ {k d}}\ frac {\ omega_ {0}} {X_ {d} ^ {\ prime}}\ da_ {d R}\\
i_ {d R} &=\ frac {X_ {a d}} {X_ {k d}}\ frac {\ omega_ {0}} {X_ {d} ^ {\ prime}}\ lambda_ {d S} -\ frac {X_ {d}} {X_ {d} ^ {\ prime}\ frac\ omega _ {0}} {X_ {k d}}\ lambda_ {d R}
\ final {alineado}\)
El eje q es el mismo.
El par puede ser, con estos cálculos para la corriente, escrito como:
\ T_{e}=\frac{3}{2} p\left(\lambda_{d S} i_{q S}-\lambda_{q S} i_{d S}\right)=-\frac{3}{2} p \frac{\omega_{0} X_{a d}}{X_{k d} X_{d}^{\prime}}\left(\lambda_{d S} \lambda_{q R}-\lambda_{q S} \lambda_{d R}\right)
Obsérvese que aquí se mantienen los problemas habituales con las variables ordinarias: la expresión anterior se escribió asumiendo que las variables se expresan como cantidades máximas. Si
RMS se usa debemos reemplazar 3/2 por 3!
Con estos, el modelo de simulación es bastante sencillo. Las ecuaciones de estado son:
\ (\\ comenzar {array} {l}
\ frac {d\ lambda_ {d S}} {d t} =V_ {d S} +\ omega\ lambda_ {q S} -R_ {S} i_ {d S}\
\ frac {d\ lambda_ {q S}} {d t} =V_ {q S} -\ omega\ lambda_ {d S} -R_ {S} i_ {q S}\
\ frac {d\ lambda_ {d R}} {d t} =\ omega_ {s}\ lambda_ {q R} -R_ {R} i_ {d R}\
\ frac {d\ lambda _ {q R}} {d t} =-\ omega_ {s}\ lambda_ {d R} -R_ {S} i_ {q R}\
\ frac {d\ Omega_ {m}} {d t} =\ frac {1} {J}\ left (T_ {e} +T_ {m}\ derecha)
\ end {array}\)
donde la frecuencia del rotor (frecuencia de deslizamiento) es:
\ \omega_{s}=\omega-p \Omega_{m}
Para simulaciones simples y frecuencia de excitación constante, la elección de los sistemas de coordenadas es arbitraria, por lo que podemos elegir algo conveniente. Por ejemplo, podríamos optar por fijar el sistema de coordenadas a un marco que gira sincrónicamente, de modo que la frecuencia del estator\ \omega=\omega_{0}. En este caso, podríamos escoger el voltaje del estator para que se encuentre en un eje u otro. Una elección común es\ V_{d}=0 y\ V_{q}=V.
Modelo de control
Si vamos a convertir la máquina en un servomotor, vamos a querer ser un poco más sofisticados sobre nuestro sistema de coordenadas. En general, el principio de control orientado al campo es muy parecido a emular la función de una máquina de CC (conmutador). Descubrimos dónde está el flujo, luego inyectamos corriente para interactuar más directamente con el flujo.
Como primer paso, tenga en cuenta que debido a que los dos enlaces de flujo del estator son la suma del entrehierro y el flujo de fuga,
\ (\\ comenzar {alineado}
\ lambda_ {d S} &=\ lambda_ {a g d} +L_ {S\ ell} i_ {d S}\
\ lambda_ {q S} &=\ lambda_ {a g q} +L_ {S\ ell} i_ {q S}
\ final {alineado}\)
Esto significa que podemos reescribir el torque como:
\ T^{e}=\frac{3}{2} p\left(\lambda_{a g d} i_{q S}-\lambda_{a g q} i_{d S}\right)
A continuación, tenga en cuenta que el flujo del rotor está, de manera similar, relacionado con el flujo entre aire:
\ (\\ comenzar {alineado}
\ lambda_ {a g d} &=\ lambda_ {d R} -L_ {R\ ell} i_ {d R}\
\ lambda_ {a g q} &=\ lambda_ {q R} -L_ {R\ ell} i_ {q R}
\ final {alineado}\)
El par ahora se convierte en:
\ T^{e}=\frac{3}{2} p\left(\lambda_{d R} i_{q S}-\lambda_{q R} i_{d S}\right)-\frac{3}{2} p L_{R \ell}\left(i_{d R} i_{q S}-i_{q R} i_{d S}\right)
Ahora bien, dado que las corrientes del rotor podrían escribirse como:
\ (\\ begin {array} {l}
i_ {d R} =\ frac {\ lambda_ {d R}} {L_ {R}} -\ frac {M} {L_ {R}} i_ {d S}\\
i_ {q R} =\ frac {\ lambda_ {q R}} {L_ {R}} -\ frac {M} {L_ {R}} i_ {q S}
\ final {matriz}\)
Ese segundo término puede escribirse como:
\ i_{d R} i_{q S}-i_{q R} i_{d S}=\frac{1}{L_{R}}\left(\lambda_{d R} i_{q S}-\lambda_{q R} i_{d S}\right)
Entonces ese par es ahora:
\ T^{e}=\frac{3}{2} p\left(1-\frac{L_{R \ell}}{L_{R}}\right)\left(\lambda_{d R} i_{q S}-\lambda_{q R} i_{d S}\right)=\frac{3}{2} p \frac{M}{L_{R}}\left(\lambda_{d R} i_{q S}-\lambda_{q R} i_{d S}\right)
Estrategia orientada al campo
Lo que se hace en el control orientado al campo es establecer un flujo de rotor en una posición conocida (generalmente esta posición es el eje d de la transformación) y luego poner una corriente en el eje ortogonal (donde será más efectiva en la producción de par). Es decir, intentaremos establecer
\ (\\ begin {array} {l}
\ lambda_ {d R} =\ lambda_ {0}\
\ lambda_ {q R} =0
\ end {array}\)
Entonces el par se produce aplicando corriente en cuadratura del eje:
\ T^{e}=\frac{3}{2} p \frac{M}{L_{R}} \Lambda_{0} i_{q S}
El proceso es casi así de simple. Hay algunos detalles involucrados en averiguar dónde está el eje de cuadratura y qué tan difícil es conducir la corriente del eje directo (magnetizante).
Ahora, supongamos que podemos tener éxito en poner flujo en el eje derecho, de modo que\ \lambda_{q R}=0, entonces las dos ecuaciones de voltaje del rotor son:
\ (\\ comenzar {alineado}
0 &=\ frac {d\ lambda_ {d R}} {d t} -\ omega_ {s}\ lambda_ {q R} +r_ {R} I_ {d R}\\
0 &=\ frac {d\ lambda_ {q R}} {d t} +\ omega_ {s}\ lambda_ d {R} +r_ {R} I_ {q R}
\ final {alineado}\)
Ahora, ya que las corrientes del rotor son:
\ (\\ comenzar {alineado}
i_ {d R} &=\ frac {\ lambda_ {d R}} {L_ {R}} -\ frac {M} {L_ {R}} i_ {d S}\\
i_ {q R} &=\ frac {\ lambda_ {q R}} {L_ {R}} -\ frac {M} L_ {R}} i_ {q S}
\ final {alineado}\)
Las expresiones de voltaje se convierten, teniendo en cuenta el hecho de que no hay flujo del eje de cuadratura del rotor:
\ (\\ comenzar {alineado}
0 &=\ frac {d\ lambda_ {d R}} {d t} +r_ {R}\ izquierda (\ frac {\ lambda_ {d R}} {L_ {R}} -\ frac {M} {L_ {R}} i_ {d S}\ derecha)\\
0 &=\ omega_ {s} lambda_ {d R} -r_ {R}\ frac {M} {L_ {R}} i_ {q S}
\ final {alineado}\)
Observando que la constante de tiempo del rotor es
\ T_{R}=\frac{L_{R}}{r_{R}}
encontramos:
\ (\\ comenzar {alineado}
T_ {R}\ frac {d\ lambda_ {d R}} {d t} +\ lambda_ {d R} &=M i_ {d S}\
\ omega_ {s} &=\ frac {M} {T_ {R}}\ frac {i_ {q S}} {\ lambda_ {d R}
\ end {alineado}\)
La primera de estas dos expresiones describe el comportamiento del flujo de eje directo: como uno pensaría, tiene una relación simple de primer orden con la corriente del estator de eje directo. La segunda expresión, que describe el deslizamiento como una función de la corriente del eje de cuadratura y el flujo del eje directo, en realidad describe la rapidez con la que se gira el sistema de coordenadas giratorias para mantener el flujo en el eje directo.
Ahora, una aplicación de máquina real implica corrientes de fase\ i_{a},\ i_{b} y\ i_{c}, y estas deben derivarse de las corrientes modelo\ i_{d S} y\ i_{q s}. Esto se hace con, por supuesto, una operación matemática que utiliza un ángulo de transformación\ \theta. Y ese ángulo se deriva de la velocidad mecánica del rotor y deslizamiento calculado:
\ \theta=\int\left(p \omega_{m}+\omega_{s}\right) d t
Una estrategia generalmente buena para hacer que este tipo de sistema funcione es medir las corrientes trifásicas y derivar las corrientes de eje directo y cuadratura de ellas. Una buena estimación del flujo de eje directo se realiza haciendo pasar el flujo de eje directo a través de un filtro de primer orden. La operación complicada implica dividir la corriente del eje de cuadratura por el flujo de eje directo para obtener deslizamiento, pero esto ahora se hace fácilmente numéricamente (al igual que las operaciones trigonométricas requeridas para la transformación del sistema de coordenadas giratorias). En la Figura 16 se muestra un diagrama de bloques elmentario de un esquema (poseíble) plausible para esto.
En esta imagen partimos con valores comandados de corrientes de eje directo y cuadratura, correspondientes al flujo y par, respectivamente. Estos se traducen por una transformación de coordenadas giratorias en corrientes de fase comandadas. Esa transformación (simplemente la transformada inversa de Park) utiliza el ángulo q derivado como parte del esquema. En algunas implementaciones (baratas) de este esquema se utilizan las corrientes comandadas en lugar de las corrientes medidas para establecer el flujo y el deslizamiento.
Hemos mostrado las corrientes comandadas\ i_{a}^{*}, etc. como entradas a un “Amplificador”. Esto podría implementarse como una fuente de corriente PWM, por ejemplo, y un bucle apretado aquí resulta en un sistema servo de rendimiento bastante alto.
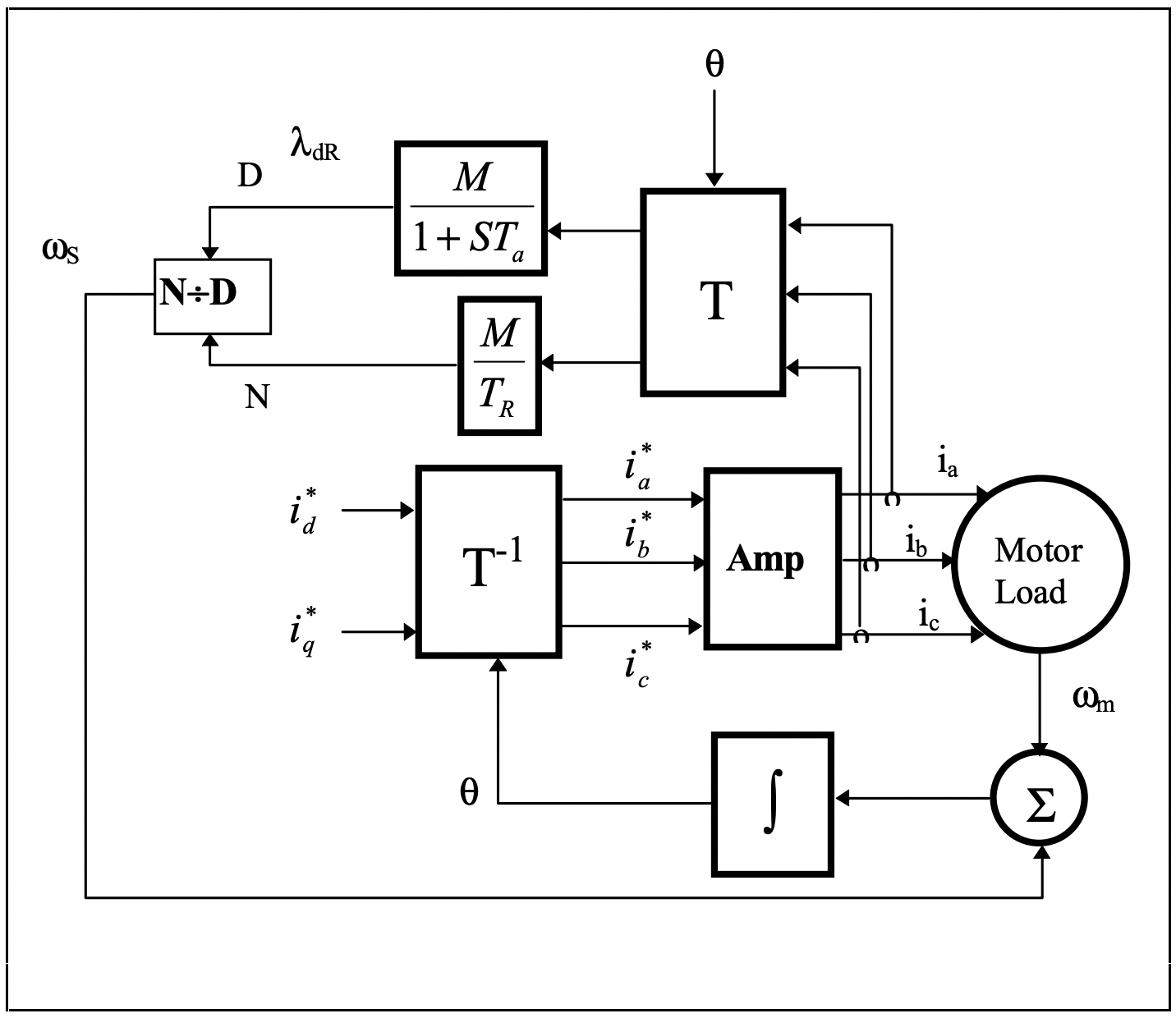 Figura 16: Controlador orientado al campo
Figura 16: Controlador orientado al campoReferencias
Ecuación\ ref {1} P.L. Alger, “Máquinas de inducción”, Gordon y Breach, 1969
 Figura 17: Circuito equivalente extendido
Figura 17: Circuito equivalente extendido

