11.1: Introducción

Prácticamente todas las máquinas eléctricas, y todas las máquinas eléctricas prácticas emplean alguna forma de sistema de campo/corriente giratoria o alterna para producir torque. Si bien es posible producir una máquina “verdadera CC” (por ejemplo, el “Disco Faraday”), por razones prácticas tales máquinas no han alcanzado la aplicación y es poco probable que lo hagan. En las máquinas que hemos examinado hasta ahora la máquina es operada desde una fuente de voltaje alterno. En efecto, esta es una de las principales razones para emplear CA en sistemas de energía.

Las primeras máquinas eléctricas emplearon un interruptor mecánico, en forma de sistema de escobilla/colector de carbón, para producir este campo giratorio. Si bien el uso generalizado de la electrónica de potencia está haciendo que los motores “sin escobillas” (que en realidad son solo máquinas síncronas) sean más populares y comunes, las máquinas de conmutación siguen siendo económicamente muy importantes. Son relativamente baratos, particularmente en tamaños pequeños, tienden a ser robustos y simples.

Encontrará máquinas de conmutación en una amplia gama de aplicaciones. El motor de arranque en todos los automóviles es una máquina conmutadora conectada en serie. Muchos de los otros motores eléctricos en los automóviles, desde los pequeños motores que impulsan los espejos retrovisores exteriores hasta los motores que impulsan los limpiaparabrisas son máquinas de conmutación de imán permanente. Los grandes motores de tracción que impulsan trenes subterráneos y locomotoras diesel/eléctricas son máquinas de conmutación de CC (aunque las máquinas de inducción están haciendo algunas incursiones aquí). Y muchos aparatos comunes utilizan motores “universales”: motores de colector conectados en serie adaptados a CA.

Geometría

En 1 se muestra una imagen esquemática (“caricatura”) de una máquina tipo conmutador. La armadura de esta máquina está en el rotor (esta es la parte que maneja la energía eléctrica), y la corriente se alimenta a la armadura a través del sistema de escobilla/conmutador. Se proporciona el campo magnético de interacción

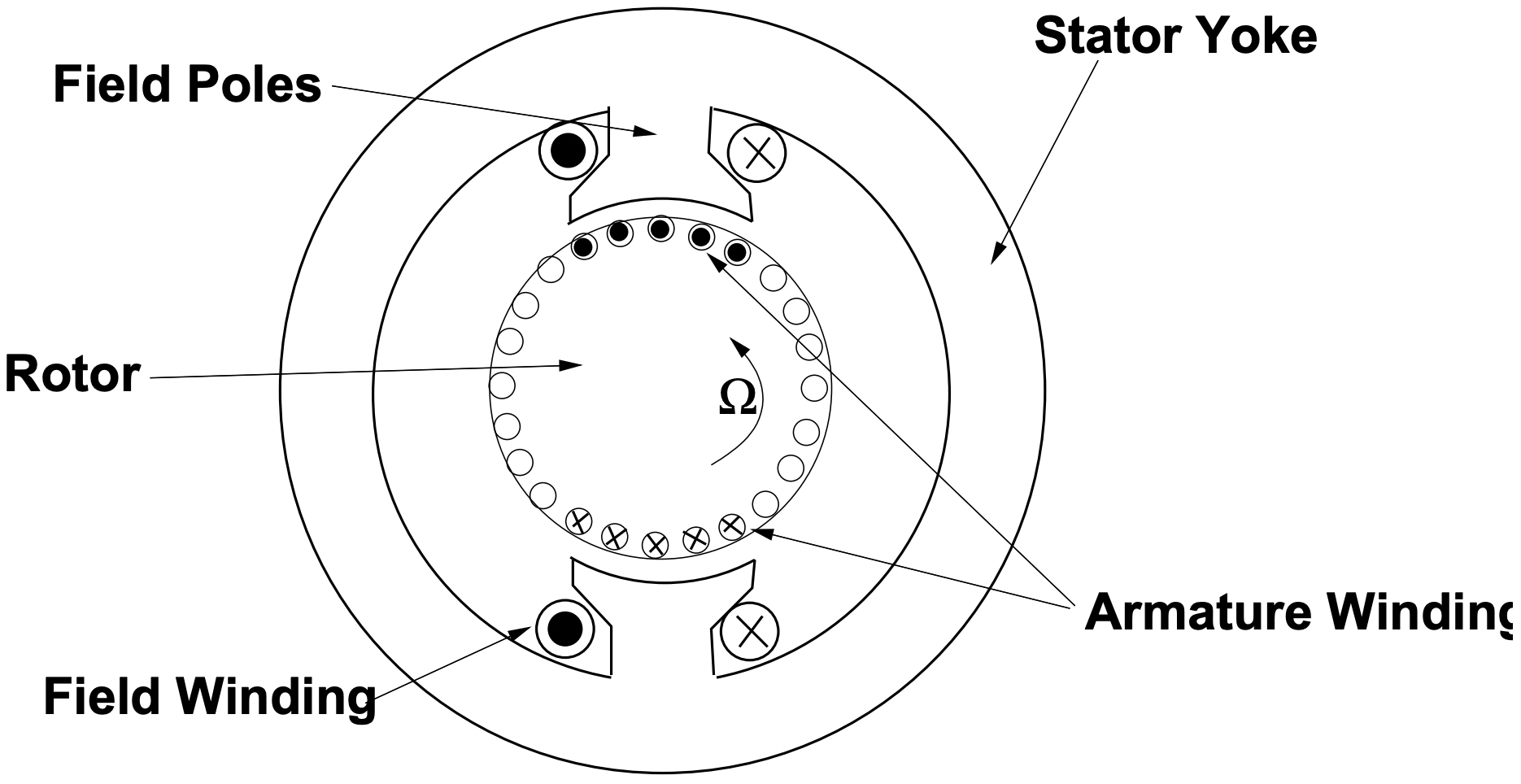Figura 1: Geometría de Máquina DC de Campo Herido

(en esta imagen) por un devanado de campo. Un campo de imán permanente es aplicable aquí, y vamos a tener mucho más que decir sobre este tipo de arreglos a continuación.

Ahora bien, si asumimos que la densidad de flujo magnético de interacción promedia\(\ B_{r}\), y si hay\(\ C_{a}\) conductores debajo de los polos en cualquier momento, y si hay m trayectorias paralelas, entonces podemos estimar el par producido por la máquina por:

\(\ T_{e}=\frac{C_{a}}{m} R \ell B_{r} I_{a}\)

donde\(\ R\) y\(\ \ell\) son el radio y la longitud del rotor, respectivamente y\(\ I_{a}\) es corriente terminal. Tenga en cuenta que no\(\ C_{a}\) es necesariamente el número total de conductores, sino más bien el número total de conductores activos (es decir, conductores debajo del polo y por lo tanto sujetos al campo de interacción). Ahora bien, si observamos\(\ N_{f}\) como el número de giros de campo por polo, el campo de interacción es solo:

\(\ B_{r}=\frac{N_{f} I_{f}}{g}\)

lo que lleva a una expresión simple para el par en términos de las dos corrientes:

\(\ T_{e}=G I_{a} I_{f}\)

donde G es ahora el coeficiente motor (unidades de N-m/amperio al cuadrado):

\(\ G=\mu_{0} \frac{C_{a}}{m} \frac{N_{f}}{g} R \ell\)

Ahora, volvamos y veamos esto desde el punto de vista del voltaje. Comience con la Ley de Faraday:

\(\ \nabla \times \vec{E}=-\frac{\partial \vec{B}}{\partial t}\)

Integrando ambos lados y señalando que el área integral de un rizo es el borde integral de la cantidad, encontramos:

\(\ \oint \vec{E} \cdot d \bar{\ell}=-\iint \frac{\partial \vec{B}}{\partial t}\)

Ahora bien, eso es un poco incómodo de usar, particularmente en el caso que tenemos aquí en el que se mueve el borde del contorno (tenga en cuenta que estaremos usando esta expresión para encontrar voltaje). Podemos hacer esto un poco más cómodo de usar si observamos:

\(\ \frac{d}{d t} \iint \vec{B} \cdot \vec{n} d a=\iint \frac{\partial \vec{B}}{\partial t} \cdot \vec{n} d a+\oint \vec{v} \times \vec{B} \cdot d \vec{\ell}\)

donde\(\ \vec{v}\) está la velocidad del contorno. Esto nos da una manera conveniente de observar el campo eléctrico aparente dentro de un objeto en movimiento (como en los conductores en una máquina de CC):

\(\ \vec{E}^{\prime}=\vec{E}+\vec{v} \times \vec{B}\)

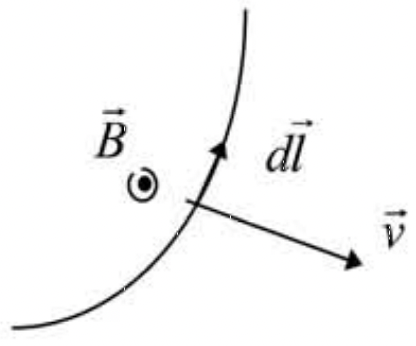Figura 2: El movimiento de un contorno a través de un campo magnético produce cambio de flujo y campo eléctrico en el contorno móvil

Ahora, tenga en cuenta que los conductores de la armadura se están moviendo a través del campo magnético producido por los polos del estator (campo), y podemos atribuirles un campo eléctrico dirigido axialmente:

\(\ E_{z}=-R \Omega B_{r}\)

Si los conductores de armadura están dispuestos como se describió anteriormente, con\(\ C_{a}\) conductores en m trayectorias paralelas debajo de los polos y con un campo magnético radial activo medio de\(\ B_{r}\), podemos calcular una tensión inducida en los conductores del estator:

\(\ E_{b}=\frac{C_{a}}{m} R \Omega B_{r}\)

Tenga en cuenta que esto es solo el voltaje inducido por el movimiento de los conductores de la armadura a través del campo y no incluye la resistencia del cepillo o del conductor. Si incluimos la expresión de campo magnético efectivo, encontramos que la contratensión es:

\(\ E_{b}=G \Omega I_{f}\)

lo que nos lleva a la conclusión de que newton-metros por amperio cuadrado equivale a voltios segundos por amperio. Esto es razonable si examinamos la energía eléctrica en la interacción y la salida de energía mecánica:

\(\ P_{e m}=E_{b} I_{a}=T_{e} \Omega\)

Ahora, un modelo más completo de esta máquina incluiría los efectos de resistencia de armadura, cepillo y plomo, de manera que en funcionamiento en estado estacionario:

\(\ V_{a}=R_{a} I_{a}+G \Omega I_{f}\)

Ahora, considere esta máquina con su armadura conectada a una fuente de voltaje y su campo operando a corriente constante, de manera que:

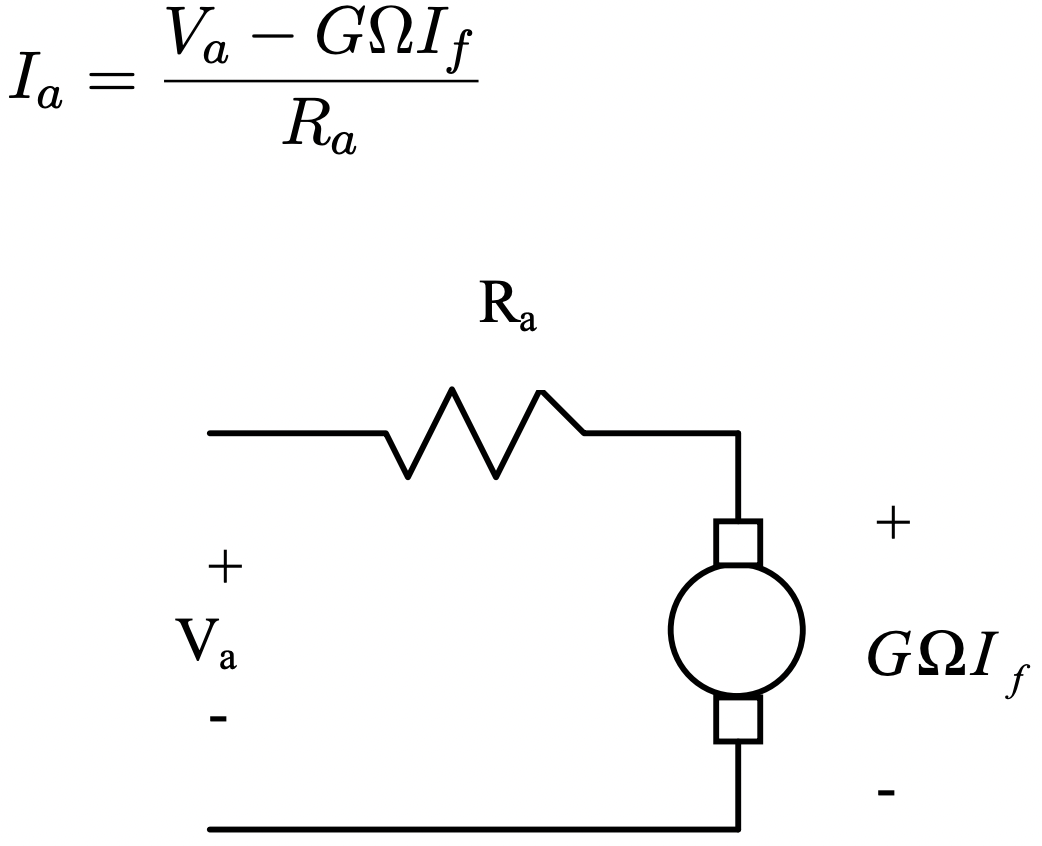Figura 3: Circuito equivalente a máquina de CC

Luego, el par, la entrada de energía eléctrica y la salida de energía mecánica son:

\ (\\ comenzar {alineado}
T_ {e} &=G I_ {f}\ frac {V_ {a} -G\ Omega I_ {f}} {R_ {a}}\
P_ {e} &=V_ {a}\ frac {V_ {a} -G\ Omega I_ {f}} {R_ {a}}\
P_ {m} &=G\ Omega I_ {f}\ frac {V_ {a} -G\ Omega I_ {f}} {R_ {a}}
\ final {alineado}\)

Ahora bien, tenga en cuenta que estas expresiones definen tres regímenes definidos por la velocidad de rotación. Los dos “puntos de ruptura” están a velocidad cero y a la velocidad de “par cero”:

\(\ \Omega_{0}=\frac{V_{a}}{G I_{f}}\)

Porque\(\ 0<\Omega<\Omega_{0}\), la máquina es un motor: la entrada de energía eléctrica y la salida mecánica son ambas positivas. Para velocidades más altas:\(\ \Omega_{0}<\Omega\), la máquina es un generador, siendo ambas negativas la potencia eléctrica de entrada y la salida mecánica. Para velocidades inferiores a cero, la entrada de energía eléctrica es positiva y la salida mecánica es negativa. Hay pocas necesidades para operar máquinas en este régimen, a falta de algunos tipos de “taponamiento” o frenado de emergencia en sistemas de tracciones.

Conexiones

Acabamos de describir un modo de funcionamiento de una máquina conmutadora generalmente llamada “excitada por separado”, en la que los circuitos de campo y armadura se controlan por separado. Este modo de operación se utiliza en algunos tipos de aplicaciones de tracción en las que la flexibilidad que brinda es útil. Por ejemplo,

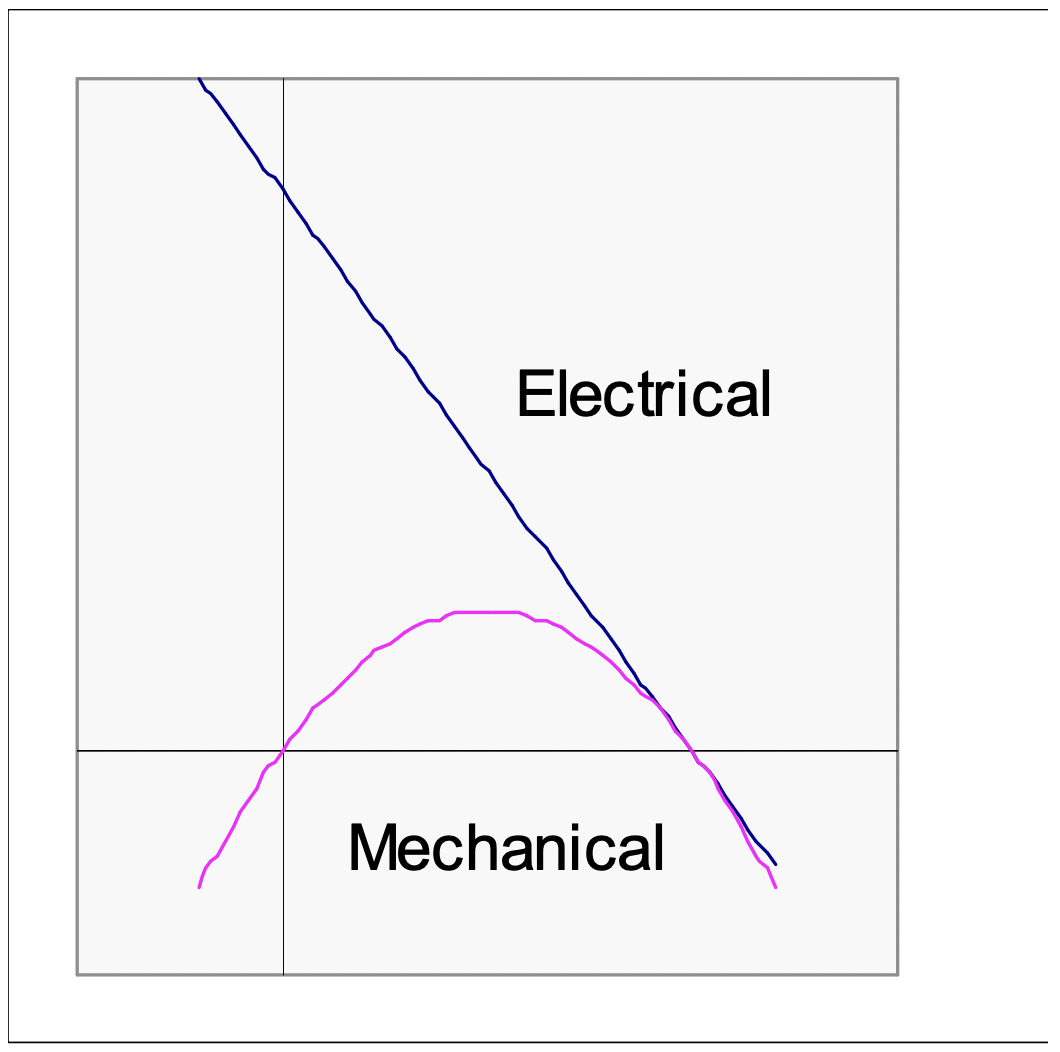Figura 4: Regímenes operativos de la máquina de CC

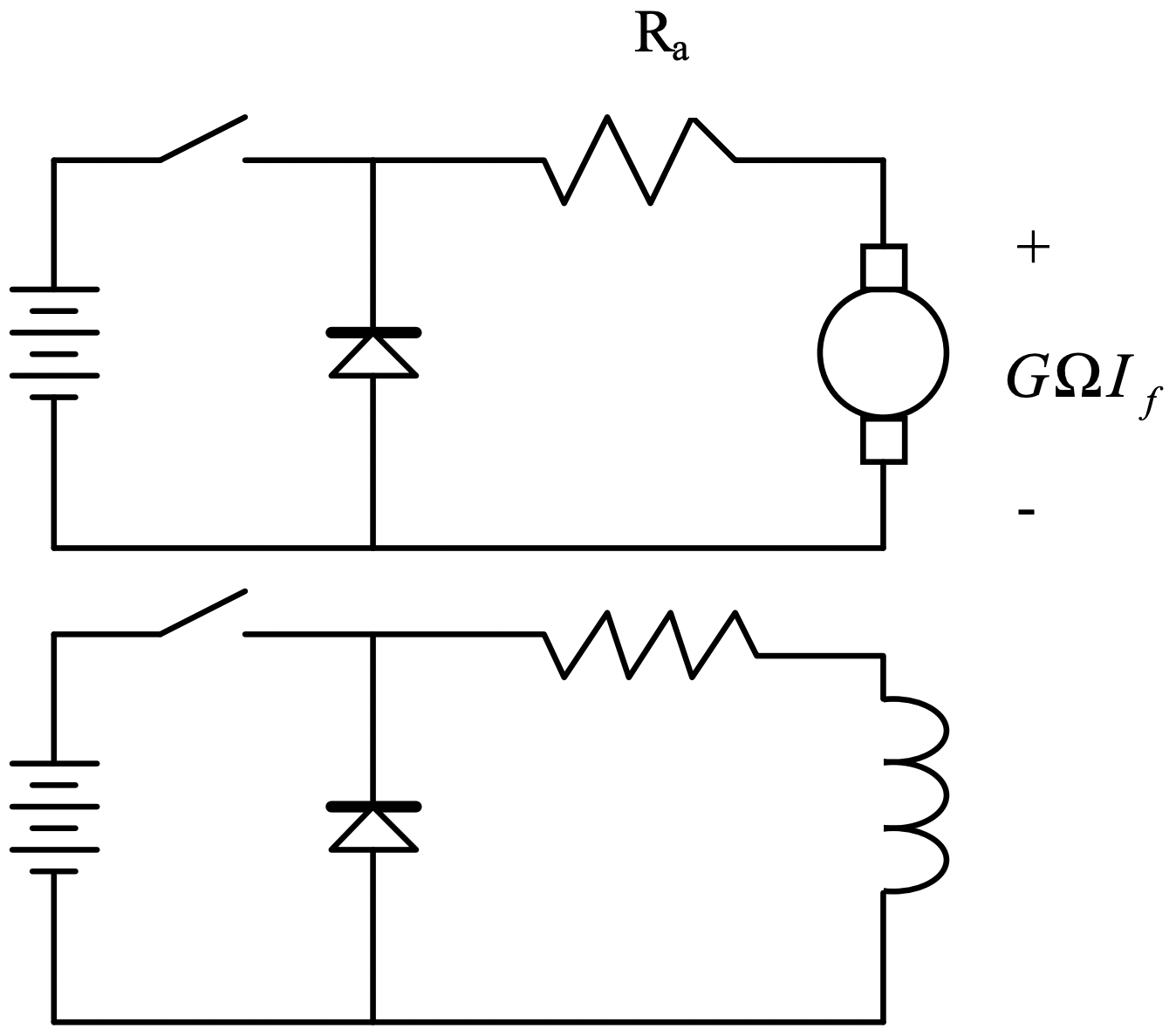Figura 5: Conexión de máquina excitada por separado con dos Chopper

algunas aplicaciones de tracción aplican control de voltaje en forma de “choppers” a máquinas excitadas por separado.

Tenga en cuenta que la “velocidad de par cero” depende del voltaje de la armadura y de la corriente de campo. Para un par alto a baja velocidad, se operaría la máquina con alta corriente de campo y suficiente voltaje de armadura para producir la corriente requerida. A medida que aumenta la velocidad, también lo hace el voltaje de retorno, y la corriente de campo puede necesitar reducirse. A cualquier velocidad de funcionamiento constante, habrá una mezcla óptima de corrientes de campo y armadura para producir el par requerido. Para frenar uno podría (y esto a menudo se hace) volver a conectar la armadura de la máquina a una resistencia de frenado y convertir la máquina en un generador. El par de frenado es controlado por la corriente de campo.

Un subconjunto de la máquina excitada por separado es la conexión de derivación en la que la armadura y el campo son suministrados por la misma fuente, en paralelo. Esta conexión ya no es ampliamente utilizada: no produce ninguna capacidad significativa para controlar la velocidad y las aplicaciones simples a las que se utiliza están siendo manejadas principalmente por máquinas de inducción.

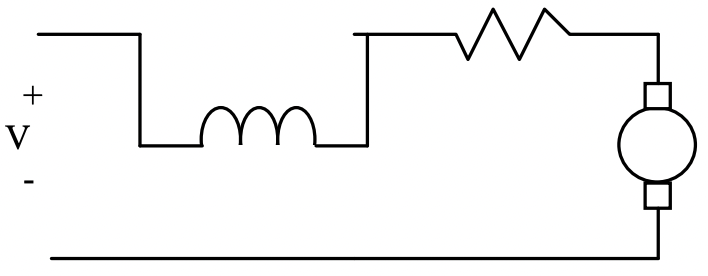Figura 6: Conexión en serie

Otra conexión que todavía es ampliamente utilizada en la conexión en serie, en la que el devanado de campo está dimensionado de manera que su nivel de corriente de funcionamiento normal sea el mismo que la corriente normal de la armadura y los dos devanados estén conectados en serie. Entonces:

\(\ I_{a}=I_{f}=\frac{V}{R_{a}+R_{f}+G \Omega}\)

Y luego el par es:

\(\ T_{e}=\frac{G V^{2}}{\left(R_{a}+R_{f}+G \Omega\right)^{2}}\)

Es importante señalar que esta máquina no tiene velocidad de “par cero”, lo que lleva a la posibilidad de que una máquina descargada pueda acelerar a velocidades peligrosas. Esto es particularmente cierto porque el conmutador, hecho de piezas de material relativamente pesado atadas entre sí con no conductores, no es muy fuerte.

El control de velocidad de las máquinas conectadas en serie se puede lograr con control de voltaje y muchos electrodomésticos que utilizan este tipo de máquina utilizan picadoras o control de fase. Una forma más antigua de control utilizada en aplicaciones de tracción era la resistencia de caída en serie: obviamente no es una forma muy eficiente de controlar la máquina y no ampliamente utilizada (excepto en equipos antiguos, por supuesto).

Una variación de esta clase de máquina es el “motor universal” muy ampliamente utilizado, en el que tanto el estator como el rotor (campo y armadura) de la máquina están construidos para operar con corriente alterna. Esto significa que tanto el campo como la armadura están hechos de acero laminado. Tenga en cuenta que una máquina de este tipo funcionará igual que lo tendría con corriente continua, siendo la única adición la impedancia reactiva de los dos devanados. Trabajando con cantidades RMS:

\ (\\ comenzar {alineado}
\ subrayado {I} &=\ frac {\ subrayado {V}} {R_ {a} +R_ {f} +G\ omega+J\ omega\ izquierda (L_ {a} +L_ {f}\ derecha)}\
T_ {e} &=\ frac {|\ subrayado {V} |^ {2}} {izquierda\ (R_ {a} +R_ {f} +G\ Omega\ derecha) ^ {2} +\ izquierda (\ omega L_ {a} +\ omega L_ {f}\ derecha) ^ {2}}
\ final {alineado}\)

donde\(\ \omega\) está la frecuencia de suministro eléctrico. Tenga en cuenta que, a diferencia de otras máquinas de CA, el motor universal no está limitado en velocidad a la frecuencia de suministro. Los motores de electrodomésticos suelen girar sustancialmente más rápido que el límite de 3,600 RPM de los motores de CA, y esta es una de las razones por las que se usan tan ampliamente: con las altas velocidades de rotación es posible producir más potencia por unidad de masa (y más potencia por dólar).

Conmutador

El conmutador es lo que hace que esta máquina funcione. El sistema de cepillo y conmutador de esta clase de motores implica bastante “arte negro”, y todavía hay aspectos de su funcionamiento que son poco conocidos. Sin embargo, podemos hacer algún intento de mostrar un poco de lo que hace el sistema de cepillo/colector.

Para comenzar, eche un vistazo a la imagen que se muestra en la Figura 7. Se representan un par de postes (sombreados) y un par de pinceles. Los conductores forman un grupo de caminos cerrados. La corriente de uno de los pinceles toma dos caminos paralelos. Puedes seguir uno de esos caminos alrededor de un bucle cerrado, debajo de cada uno de los dos polos (recuerda que los polos son de polaridad opuesta) al pincel opuesto. Los segmentos de conmutador abiertos (la mayoría de ellos) no transportan corriente dentro o fuera de la máquina.

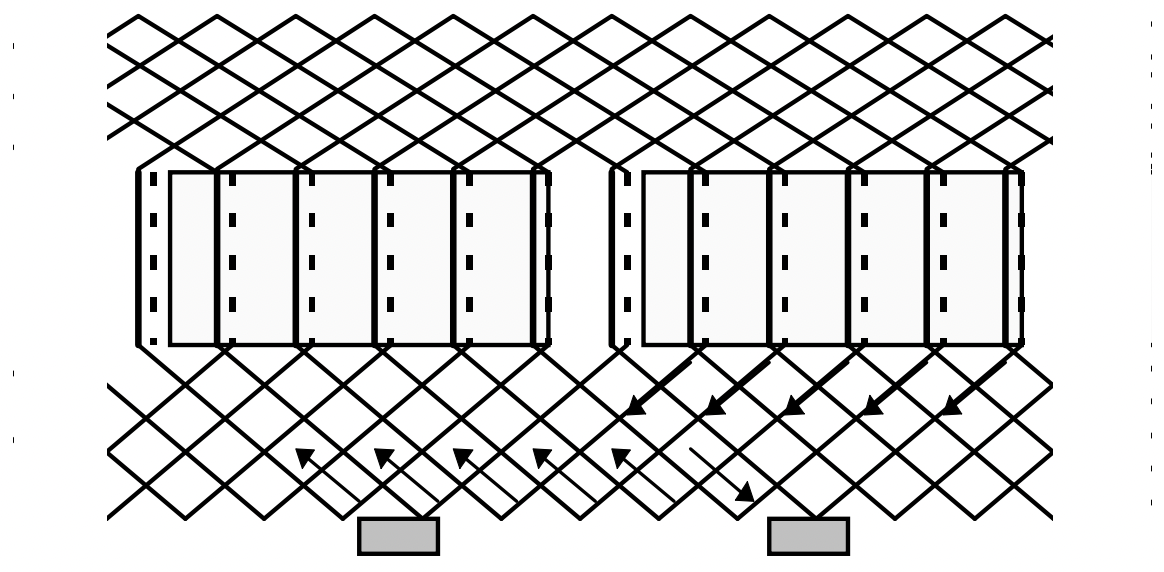Figura 7: Conmutador y trayectorias de corriente

Un intervalo de conmutación ocurre cuando se debe invertir la corriente en una bobina. (Ver Figura 8 En la forma más simple esto implica un puente de cepillo entre dos segmentos del colector, cortocircuitando esa bobina. La resistencia del cepillo provoca la descomposición de la corriente. Cuando el cepillo sale del segmento principal, la corriente en la bobina principal debe revertirse.

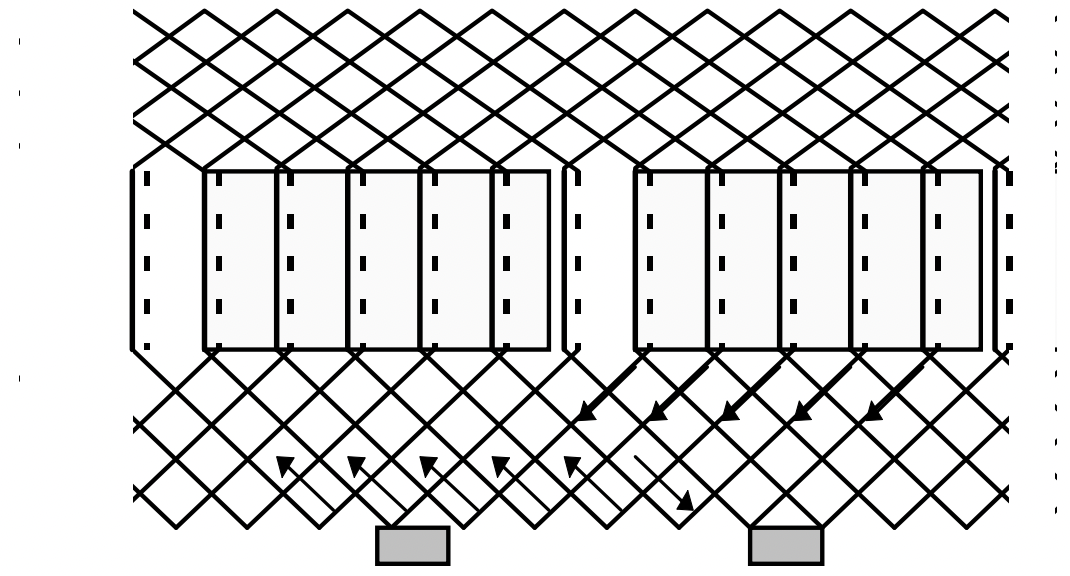Figura 8: Conmutador en Conmutación

No intentaremos entender completamente el proceso de conmutación en este tipo de máquinas, pero podemos anotar algunas cosas. La conmutación resistiva es el proceso en el que se basa en máquinas pequeñas.

Cuando se debe invertir la corriente en una bobina (porque ha dejado un polo y se acerca al otro), esa bobina es cortocircuitada por una de las escobillas. La resistencia del cepillo hace que la corriente en la bobina se detenga. Entonces el segmento del conmutador principal sale de la escobilla la corriente DEBE revertir (la bobina trasera tiene corriente en ella), y a menudo hay chispas.

Conmutación

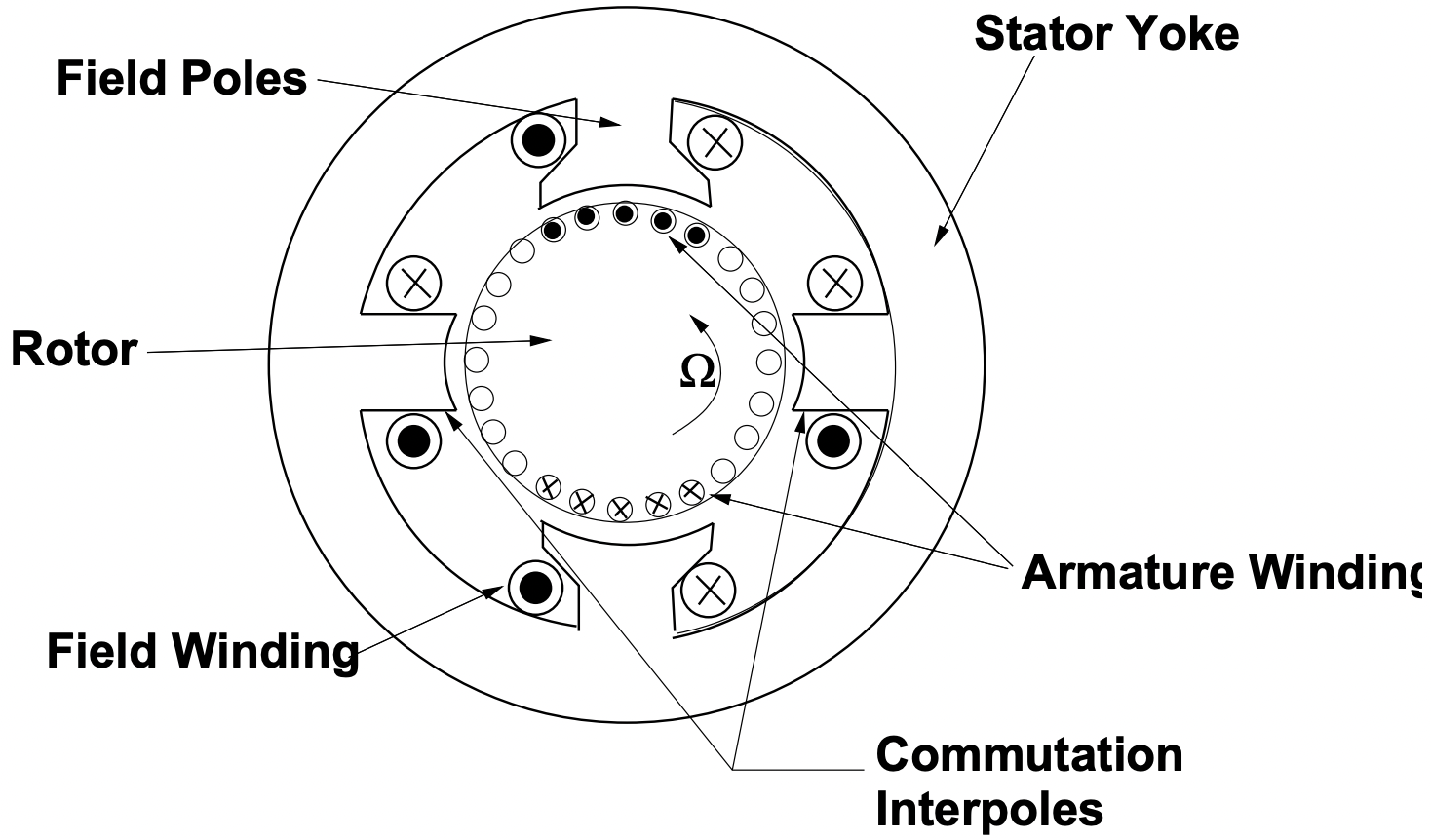Figura 9: Interpolos de conmutación

En máquinas más grandes el proceso de conmutación implicaría demasiadas chispas, lo que provoca el desgaste del cepillo, gases nocivos (ozono) que promueven la corrosión, etc. en estos casos es común usar interpolos de conmutación separados. Estas son piezas polares separadas, generalmente estrechas o aparentemente vestigales que transportan corriente de armadura. Están dispuestos de tal manera que el flujo del interpolo impulsa la corriente en la bobina conmutada en la dirección adecuada. Recuerde que la bobina que se está conmutando se encuentra físicamente entre los polos activos y el interpolo está por lo tanto en el punto correcto para influir en la conmutación. El interpolo se enrolla con corriente de armadura (está en serie con los cepillos principales). Es fácil ver que el interpolo debe tener una densidad de flujo proporcional a la corriente a conmutar. Dado que la velocidad con la que se debe conmutar la bobina es proporcional a la velocidad de rotación y también lo es el voltaje inducido por el interpolo, si se pone el número correcto de vueltas alrededor del interpolo, la conmutación se puede hacer para que sea bastante precisa.

Compensación

El análisis de las máquinas de conmutación a menudo ignora el flujo de reacción de la armadura. Obviamente estas máquinas DO producen flujo de reacción de armadura, en cuadratura con el campo principal. Normalmente, las máquinas de conmutación son altamente sobresalientes y la inductancia en cuadratura es menor que la inductancia de eje directo, pero todavía se produce flujo. Esto se suma a la densidad de flujo en un lado de los polos principales (posiblemente conduciendo a la saturación). Para que la distribución del flujo sea más uniforme y por lo tanto para evitar este efecto de saturación del flujo del eje de cuadratura, es común en máquinas de muy alta calificación enrollar bobinas de compensación: esencialmente imágenes especulares de las bobinas de armadura, pero esta vez enrolladas en ranuras en la superficie de los polos de campo. Tales bobinas tendrán el mismo número de amperios-vueltas que el

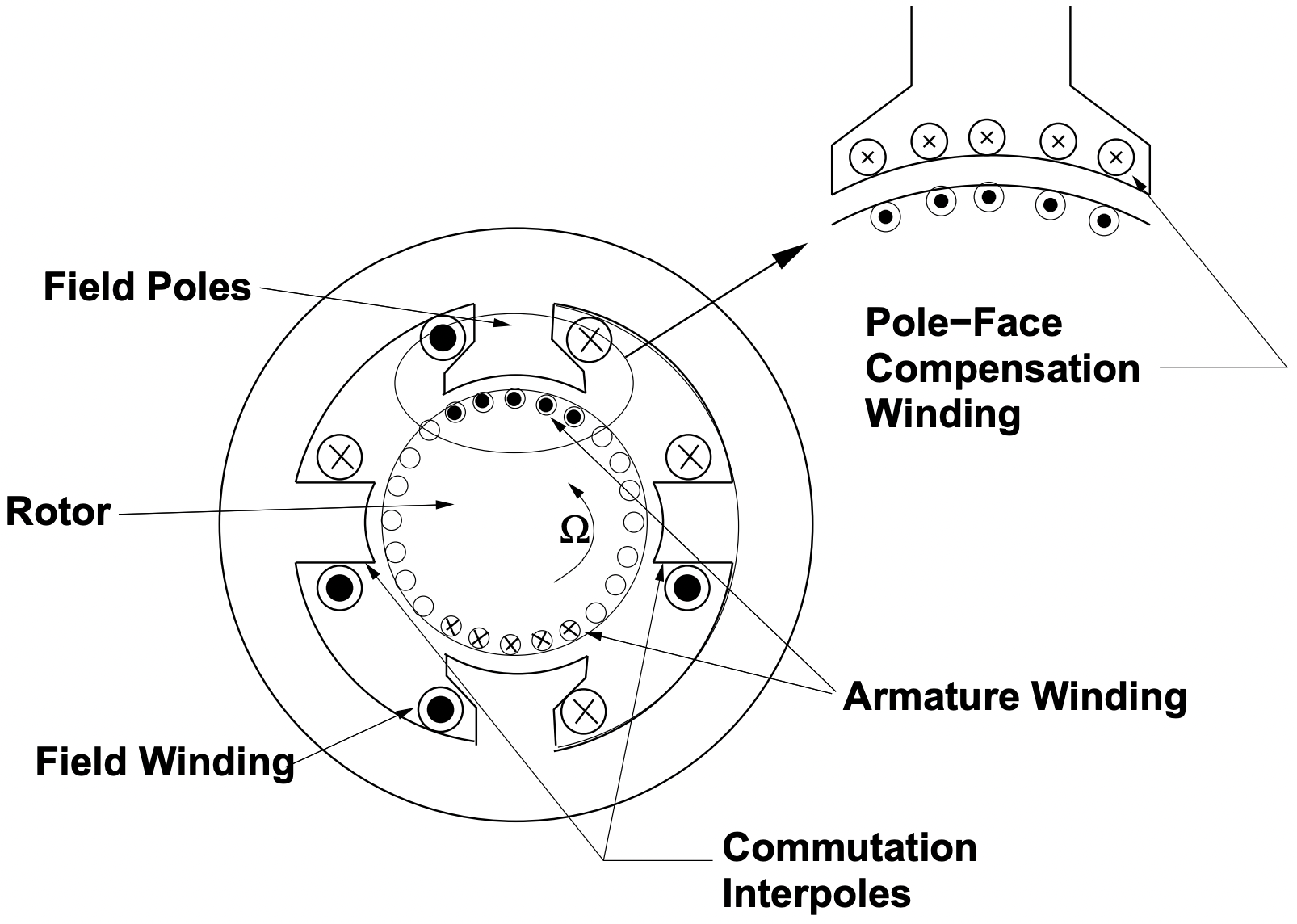Figura 10: Bobinado de compensación de cara de poste

armadura. Normalmente tienen el mismo número de vueltas y se conectan directamente en serie con los cepillos de armadura. Lo que hacen es cancelar casi exactamente el flujo producido por las bobinas de la armadura, dejando solo el flujo principal producido por el devanado de campo. Uno podría pensar que estas bobinas proporcionan un par de reacción, producido exactamente de la misma manera que el par principal es producido por la armadura. En la Figura 10 se muestra una vista de dibujos animados de esto.