11.2: Imanes Permanentes en Máquinas Eléctricas

De todos los cambios en la tecnología de materiales en los últimos años, los avances en imanes permanentes han tenido el mayor impacto en las máquinas eléctricas. Los imanes permanentes suelen ser adecuados como reemplazos para los devanados de campo en las máquinas: es decir, pueden producir el campo de interacción fundamental. Esto hace tres cosas. Primero, dado que el imán permanente no tiene pérdidas elimina la energía requerida para la excitación, generalmente mejorando la eficiencia de la máquina. Segundo, dado que eliminar la pérdida de excitación reduce la carga de calor, a menudo es posible hacer que las máquinas de PM sean más compactas. Finalmente, y menos apreciado, es el hecho de que los imanes permanentes modernos tienen densidades de fuerza coercitiva muy grandes que permiten espacios de aire mucho más grandes que los devanados de campo convencionales, y esto a su vez permite flexibilidad de diseño que puede resultar en máquinas eléctricas aún mejores.

Estas ventajas vienen no sin costo. Los materiales de imanes permanentes tienen características especiales que deben tenerse en cuenta en el diseño de la máquina. Los imanes permanentes de mayor rendimiento son cerámicas quebradizas, algunos tienen sensibilidades químicas, todos son sensibles a altas temperaturas, la mayoría tienen sensibilidad a los campos desmagnetizantes y el diseño adecuado de la máquina requiere comprender bien los materiales. Estas notas no te convertirán en diseñadores experimentados de máquinas de imanes permanentes. Son, sin embargo, un intento de comenzar, de desarrollar algunas de las habilidades matemáticas requeridas y de señalar algunos de los temas importantes involucrados.

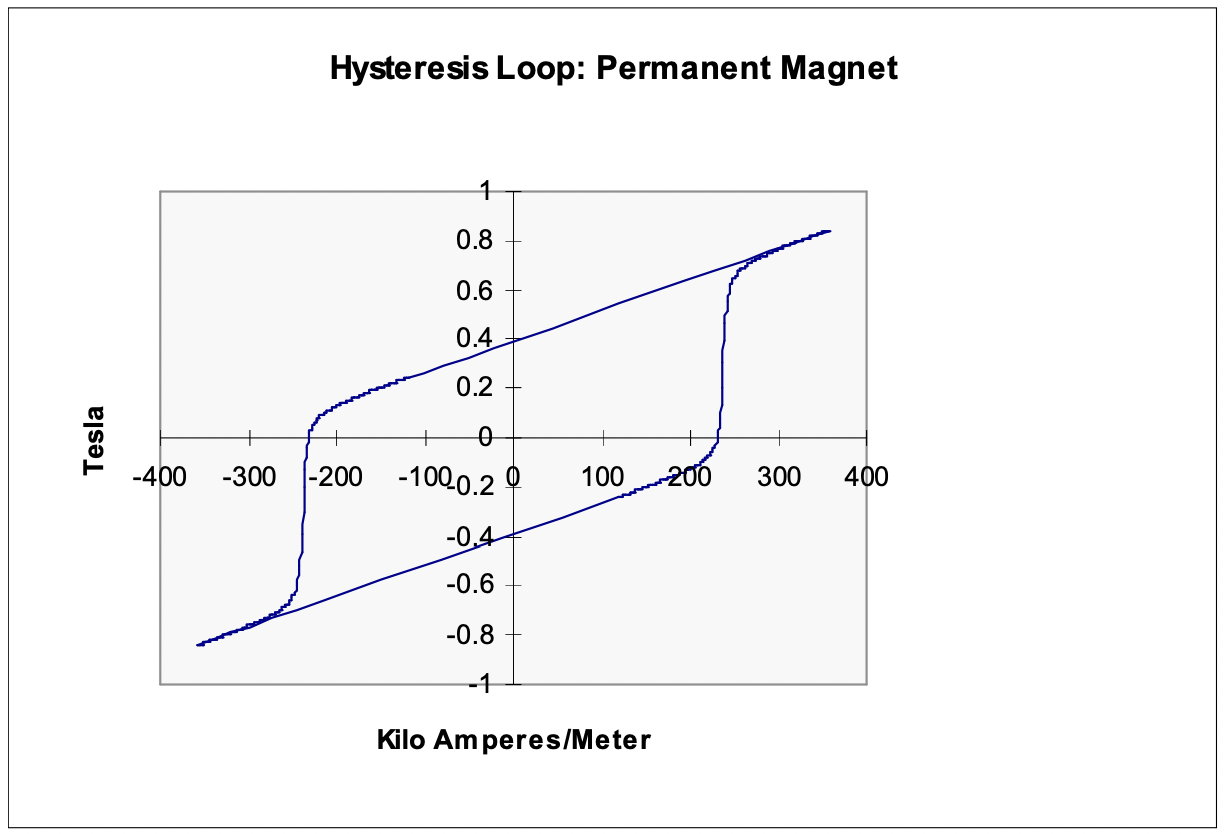Figura 11: Bucle de histéresis de imán permanente de cerámica

Los materiales de imanes permanentes son, en el núcleo, solo materiales con bucles de histéresis muy amplios. La Figura 11 es un ejemplo de algo cercano a uno de los materiales magnéticos cerámicos más populares.Tenga en cuenta que este bucle de histéresis es tan amplio que se puede ver el efecto de la permeabilidad del espacio libre.

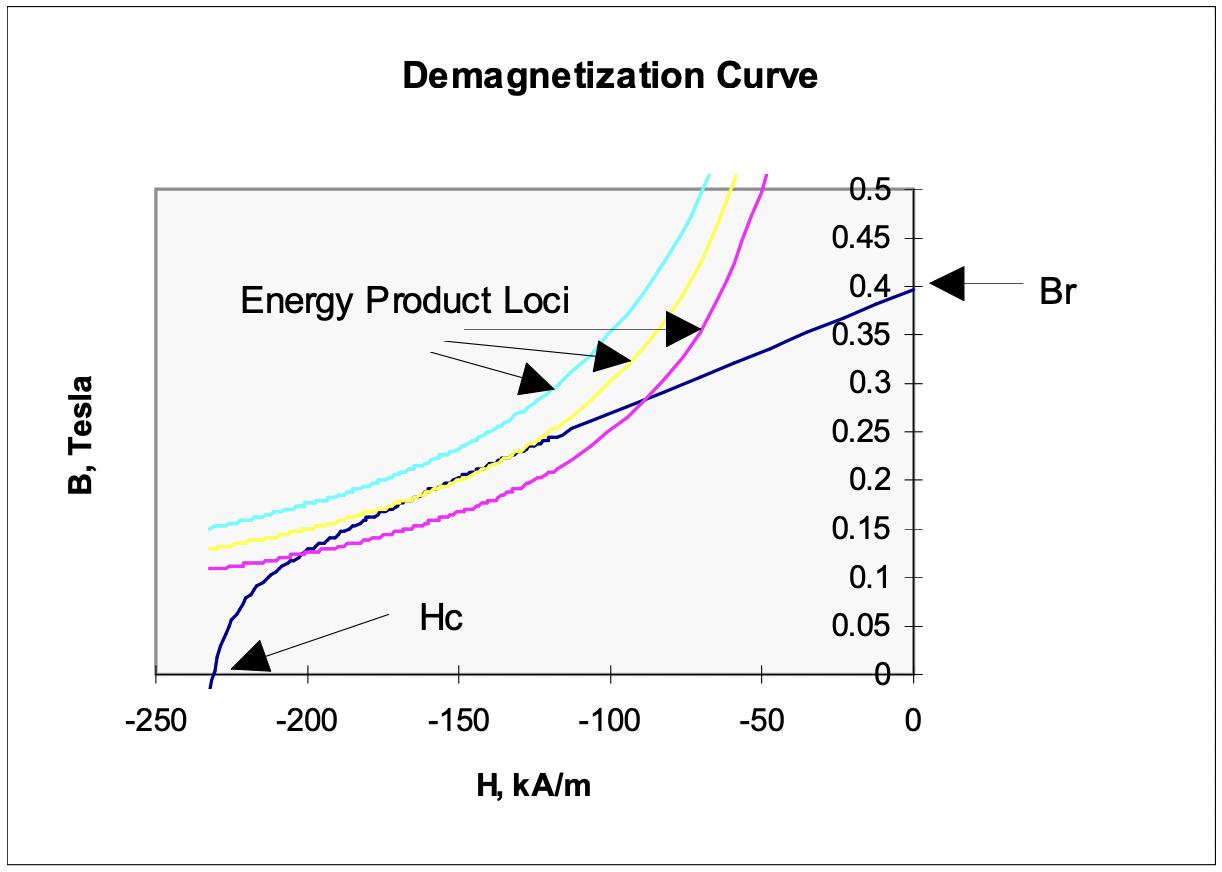Figura 12: Curva de desmagnetización

Es habitual mostrar sólo una parte de la característica magnética de los materiales de imanes permanentes (ver Figura 12), el tercer cuadrante de esta imagen, porque ahí es donde normalmente se opera el material. Tenga en cuenta algunas características importantes de lo que se llama la “curva de desmagnetización”. La densidad de flujo remanente\(\ B_{r}\), es el valor de la densidad de flujo en el material con campo magnético cero\(\ H\). El campo coercitivo\(\ H_{c}\) es el campo magnético en el que la densidad de flujo cae a cero. También se muestran en la curva loci de producto de energía constante. Desafortunadamente, esta cantidad recibe el nombre, pues aunque tiene las mismas unidades que la energía representa la energía real en un sentido bastante general. Es producto de la densidad de flujo y la intensidad de campo. Como ya sabe, hay tres sistemas de unidades de uso común para cantidades de campo magnético, y estos sistemas a menudo se mezclan para formar unidades muy confusas. Intentaremos mantenernos alejados del sistema inglés de unidades en el que la intensidad de campo\(\ H\) se mide en amperios por pulgada y densidad de flujo\(\ B\) en líneas (en realidad, generalmente kilolinas) por pulgada cuadrada. En unidades CGS la densidad de flujo se mide en Gauss (o kilogauss) y la intensidad del campo magnético en Oersteds. Y en SI la unidad de densidad de flujo es el Tesla, que es un Weber por metro cuadrado, y la unidad de intensidad de campo es el Amperio por metro. De estos, sólo el último,\(\ A / m\) es obvio. Un Weber es un vo}\) Tesla. Y, finalmente, un Oersted es esa intensidad de campo requerida para producir un Gauss en la permeabilidad del espacio libre. Dado que la permeabilidad del espacio libre\(\ \mu_{0}=4 \pi \times 10^{-7} H y / m\), esto significa que un Oe es de aproximadamente 79.58 A/m. Comúnmente, el producto energético se cita en MGoE (Mega-Gauss-Oersted) s. Un MgOe es igual a\(\ 7.958 k \mathrm{~J} / \mathrm{m}^{3}\). Una medida comúnmente utilizada para el rendimiento de un material de imán permanente es el producto de energía máxima, el mayor valor de este producto a lo largo de la curva de desmagnetización.

Para comenzar a entender cómo podrían ser útiles estos materiales, considere la situación que se muestra en la Figura 13: Una pieza de material de imán permanente se envuelve en un circuito magnético con una permeabilidad efectivamente infinita. Supongamos que la cosa tiene cierta profundidad (finita) en la dirección que no puedes ver. Ahora bien, si tomamos la ley de Ampere alrededor del camino descrito por la línea punteada,

\(\ \oint \vec{H} \cdot d \vec{\ell}=0\)

ya que no hay corriente en ninguna parte del problema. Si la magnetización es hacia arriba, como indica la flecha, esto indicaría que la densidad de flujo en el material del imán permanente es igual a la densidad de flujo remanente (también hacia arriba).

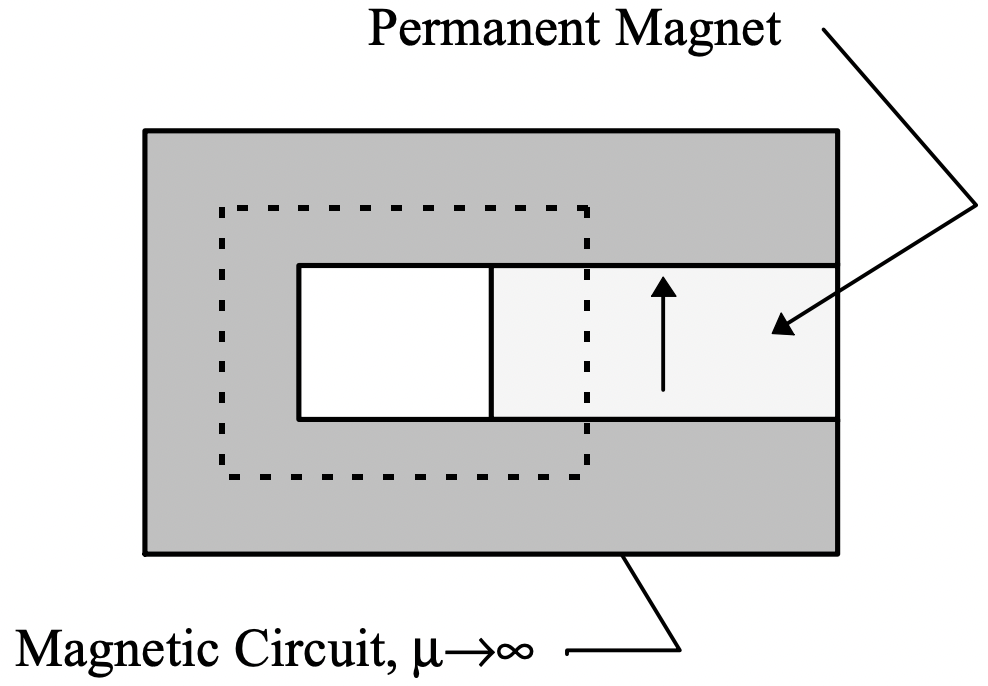Figura 13: Imán permanente en circuito magnético

Un segundo problema se ilustra en la Figura 14, en la que el mismo imán está incrustado en un circuito magnético con un entrehierro. Supongamos que el hueco tiene ancho g y área Ag. El imán tiene altura hm y área Am. Para mayor comodidad, tomaremos la dirección de referencia positiva para estar arriba (como lo vemos aquí) en el imán y hacia abajo en el entrehierro.

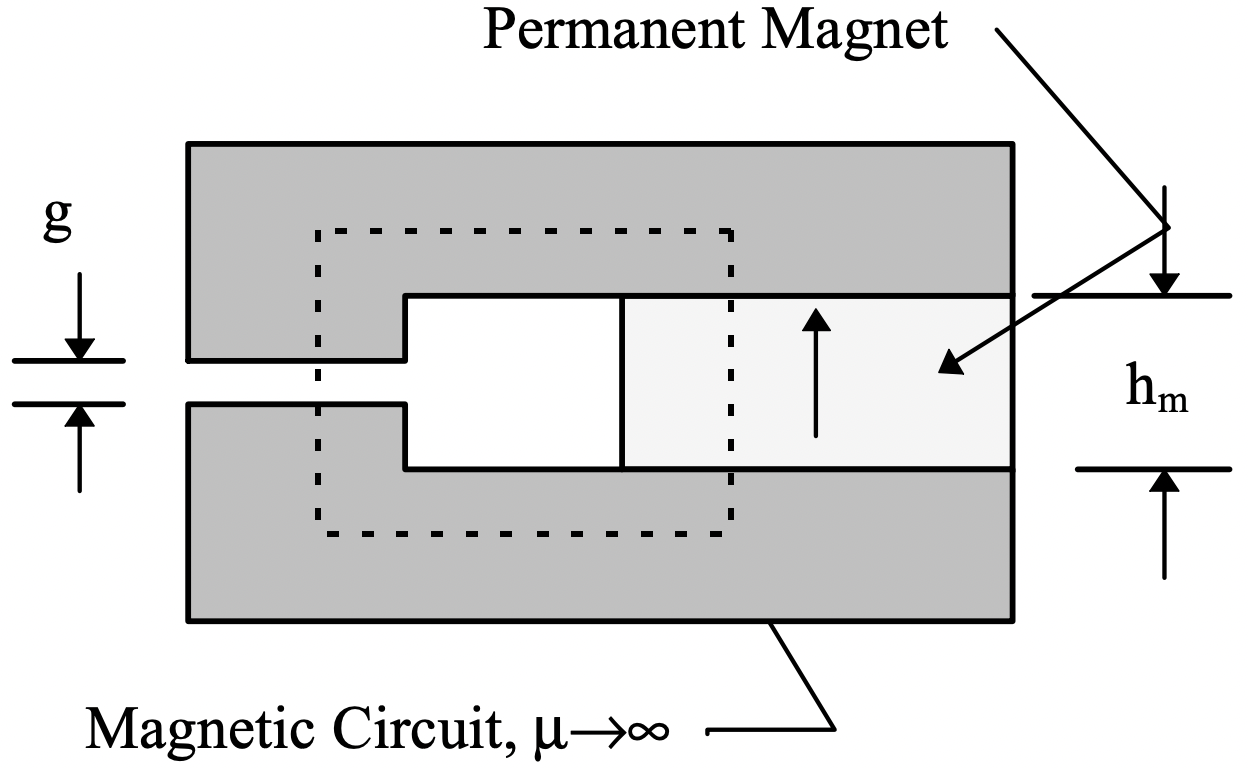Figura 14: Imán permanente que impulsa un espacio de aire

Por lo tanto, estamos siguiendo la misma dirección de referencia a medida que recorremos el bucle de la Ley de Ampere. Eso se convierte en:

\(\ \oint \vec{H} \cdot d \vec{\ell}=H_{m} h_{m}+H_{g} g\)

Ahora bien, la ley de Gauss podría escribirse para la pieza superior o inferior del circuito magnético. Suponiendo que el único flujo sustantivo que sale o entra en el circuito magnético está en el imán o en el hueco:

\(\ \oiint \vec{B} \cdot d \vec{A}=B_{m} A_{m}-\mu_{0} H_{g} A_{g}\)

Resolviendo este par tenemos:

\(\ B_{m}=-\mu_{0} \frac{A_{g}}{A_{m}} \frac{h_{m}}{g} H_{m}=\mu_{0} \mathcal{P}_{u} H_{m}\)

Esto define la permeancia unitaria, esencialmente la relación de la permeancia enfrentada al imán permanente con respecto a la permeancia interna del imán. El problema puede resolverse, si es necesario, gráficamente, ya que la relación entre\(\ B_{m}\) y\(\ H_{m}\) es inherentemente no lineal, como se muestra en la Figura 15 análisis de “línea de carga” de un circuito electrónico no lineal.

Ahora, un 'corte' más ante este problema. Tenga en cuenta que, al menos para permeancias unitarias bastante grandes, la pendiente de la característica del imán es bastante constante. De hecho, para la mayoría de los imanes permanentes utilizados en las máquinas (la única excepción importante es el imán de aleación ALNICO ahora raramente usado), generalmente es aceptable aproximar la curva de desmagnificación con:

\(\ \vec{B}_{m}=\mu_{m}\left(\vec{H}_{m}+\vec{M}_{0}\right)\)

Aquí, la magnetización\(\ M_{0}\) es fija. Además, para casi todos los materiales magnéticos prácticos, la permeabilidad del imán es casi la misma que la del espacio libre\(\ \left(\mu_{m} \approx \mu_{0}\right)\). Con eso en mente,

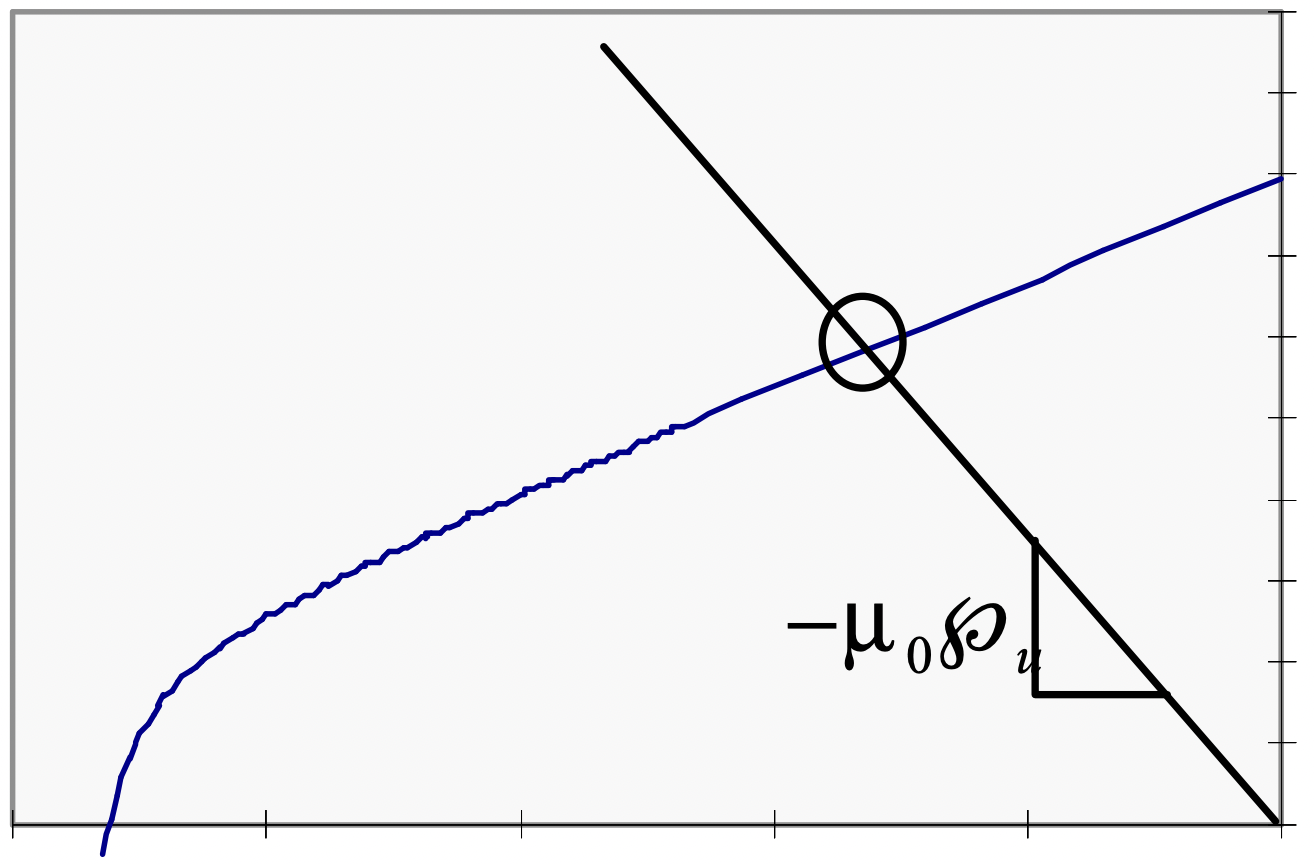Figura 15: Línea de Carga, Análisis de Permeancia Unitaria

considerar el problema mostrado en la Figura 16, en la que el imán llena sólo parte de un hueco en un circuito magnético. Pero aquí las áreas de imán y hueco son esencialmente las mismas. Podríamos considerar el imán simplemente como una magnetización.

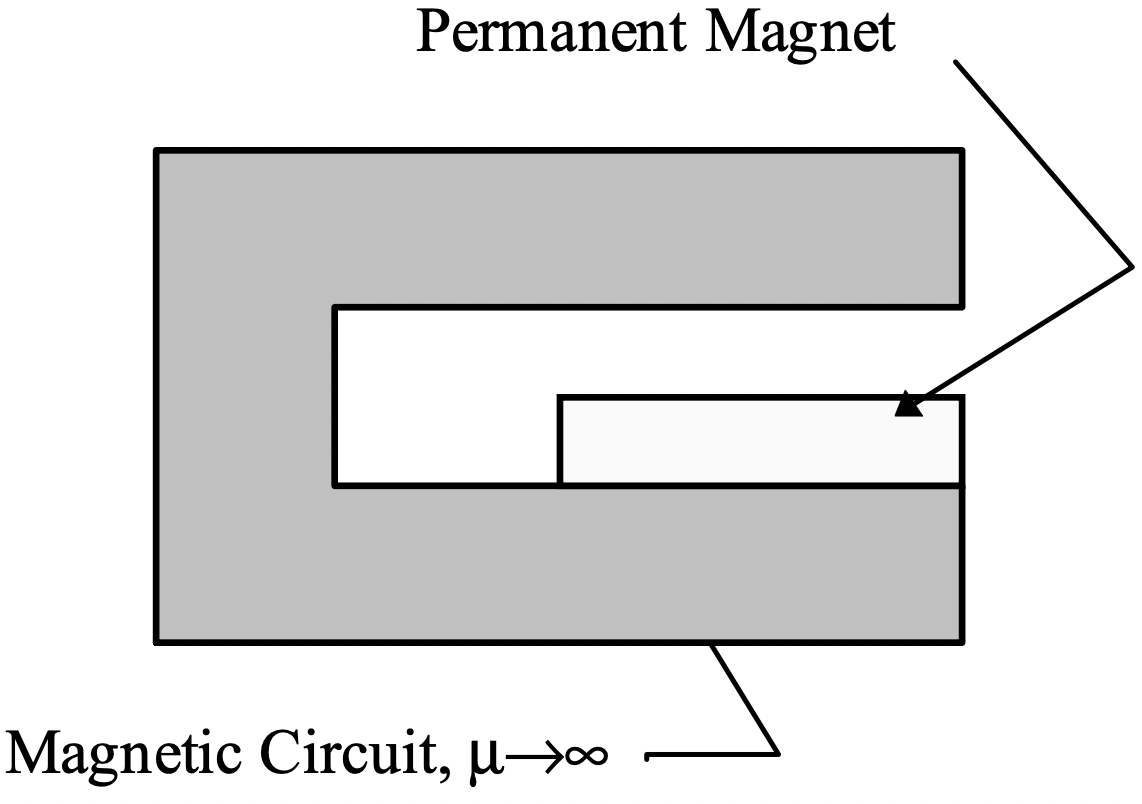Figura 16: Problema primitivo del imán superficial

En la región del imán y la brecha de aire, la Ley de Ampere y la ley de Gauss pueden escribirse:

\ (\\ comenzar {alineado}
\ nabla\ veces\ vec {H} &=0\\
\ nabla\ cdot\ mu_ {0}\ izquierda (\ vec {H} _ {m} +\ vec {M} _ _ {0}\ derecha) &=0\
\ nabla\ cdot\ mu_ {0}\ vec {H} _ {g} &=0
\ fin {alineado}\)

Ahora bien, si en el imán la magnetización es constante, la divergencia de\(\ H\) en el imán es cero. Porque aquí no hay corriente,\(\ H\) está libre de rizo, así que en todas partes:

\ (\\ comenzar {alineado}
\ vec {H} &=-\ nabla\ psi\
\ nabla^ {2}\ psi &=0
\ end {alineado}\)

Es decir, el campo magnético puede expresarse como el gradiente de un potencial escalar que satisface la ecuación de Laplace. También es bastante claro que, si podemos asignar el potencial escalar para tener un valor de cero en cualquier lugar de la superficie del circuito magnético será cero sobre todo el circuito magnético (es decir, tanto en la parte superior del hueco como en la parte inferior del imán). Por último, tenga en cuenta que en realidad no podemos suponer que el potencial escalar satisfaga la ecuación de Laplace en todas partes del problema. De hecho la divergencia de M es cero en todas partes excepto en la superficie superior del imán donde es singular! De hecho, podemos señalar que existe una densidad de carga magnética (algunos dirían ficticia):

\(\ \rho_{m}=-\nabla \cdot \vec{M}\)

En la parte superior del imán hay un cambio discontinuo en M y así el equivalente a una carga superficial magnética. Usando\(\ H_{g}\) para anotar el campo magnético sobre el imán y\(\ H_{m}\) para notar el campo magnético en el imán,

\ (\\ comenzar {alineado}
\ mu_ {0} H_ {g} &=\ mu_ {0}\ izquierda (H_ {m} +M_ {0}\ derecha)\
\ sigma_ {m} &=M_ {0} =H_ {g} -H_ {m}
\ final {alineado}\)

y luego para satisfacer la condición potencial, si hm es la altura del imán y g es el hueco:

\(\ g H_{g}=h_{m} H_{m}\)

Resolviendo,

\(\ H_{g}=M_{0} \frac{h_{m}}{h_{m}+g}\)

Ahora, se podría hacer una observación más. Produciríamos la misma densidad de flujo de entrehierro si consideramos que el imán permanente tiene una corriente superficial alrededor de la periferia igual a la intensidad de magnetización. Es decir, si la corriente superficial corre alrededor del imán:

\(\ K_{\phi}=M_{0}\)

Esto produciría un MMF en la brecha de:

\(\ F=K_{\phi} h_{m}\)

y luego como el campo magnético es solo el MMF dividido por la brecha total:

\(\ H_{g}=\frac{F}{h_{m}+g}=M_{0} \frac{h_{m}}{h_{m}+g}\)

La verdadera utilidad de los imanes permanentes proviene de las magnetizaciones relativamente grandes: son comunes números de unos pocos a varios miles de amperios por metro, y estos se traducirían en enormes densidades de corriente en imanes de tamaño ordinario.