11.3: Estructuras Simples de Máquinas de Imán Permanente- Máquinas Conmutadoras

La Figura 17 es una imagen de dibujos animados de una sección transversal de la geometría de una máquina de conmutación de dos polos que utiliza imanes permanentes. Esta es en realidad la geometría más común que se utiliza. El rotor (armadura) de la máquina es de tipo convencional, enrollados en ranuras, tal y como ya hemos visto

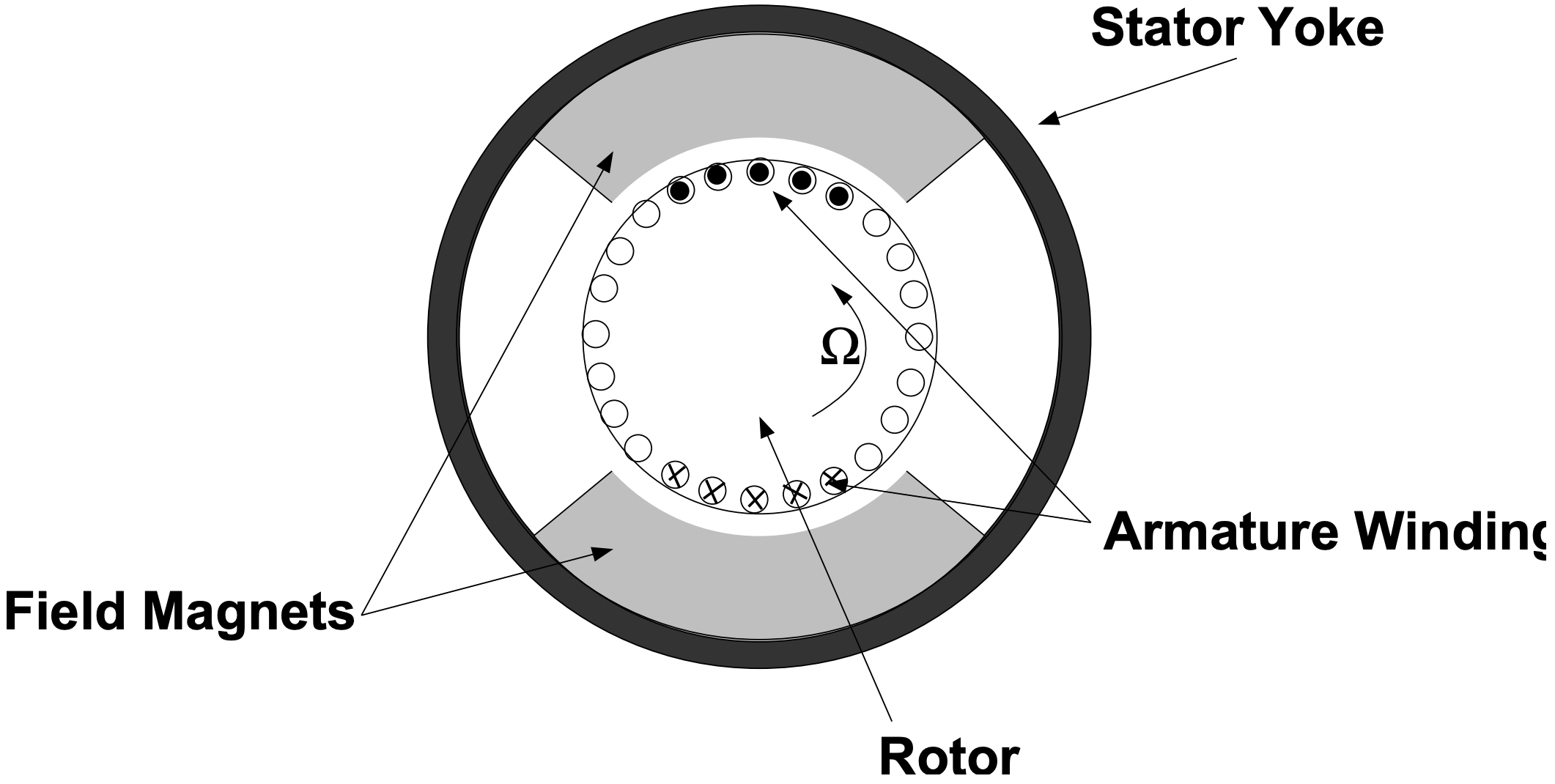Figura 17: Máquina Conmutador PM

para máquinas de conmutación. Los imanes de campo están sujetos (a menudo simplemente unidos) al interior de un tubo de acero que sirve como ruta de retorno del flujo magnético.

Supongamos a los efectos del análisis de primer orden de esta cosa que el imán es descriptible por su densidad de flujo remanente$\ B_{r}$ y tenía permeabilidad de$\ \mu_{0}$. Primero, estimaremos la densidad de flujo magnético útil y luego trataremos el voltaje generado en la armadura. Densidad de flujo de interacción Usando los fundamentos del análisis presentado anteriormente, podemos estimar la densidad de flujo magnético radial en el entrehierro como:

$\ B_{d}=\frac{B_{r}}{1+\frac{1}{\mathcal{P}_{c}}}$

donde la permeancia unitaria efectiva es:

$\ \mathcal{P}_{c}=\frac{f_{l}}{f_{f}} \frac{h_{m}}{g} \frac{A_{g}}{A_{m}}$

Un libro sobre este tema de James Ireland sugiere valores para los dos “factores de fudge”:

1. El “factor de fuga”$\ f_{l}$ se cita como de aproximadamente 1.1.
2. El “factor de reluctancia”$\ f_{f}$ se cita como aproximadamente 1.2.

Podemos estimar además la relación de áreas de la brecha y el imán por:

$\ \frac{A_{g}}{A_{m}}=\frac{R+\frac{g}{2}}{R+g+\frac{h_{m}}{2}}$

Ahora bien, hay un montón de aproximaciones y ondas de mano en esta expresión, pero parece funcionar, al menos para el tipo de máquinas contempladas.

Se requiere una segunda corrección para corregir la longitud efectiva para la interacción eléctrica. La razón de esto es que los imanes producen campos marginales, como si fueran más largos que la “longitud de pila” real del rotor (a veces lo son en realidad). Esto es puramente empírico, e Irlanda da un valor para la longitud efectiva para la generación de voltaje de:

$\ \ell_{\mathrm{eff}}=\frac{\ell^{*}}{f_{\ell}}$

dónde$\ \ell^{*}=\ell+2 N R$, y el coeficiente empírico

$\ N \approx \frac{A}{B} \log \left(1+B \frac{h_{m}}{R}\right)$

donde

\ (\\ comenzar {alineado}
B &=7.4-9.0\ frac {h_ {m}} {R}\\
A &=0.9
\ end {alineado}\)

Voltaje

Es, en este caso, más sencillo considerar primero el voltaje generado en un solo cable. Si la máquina está funcionando a velocidad angular Ω, el voltaje de velocidad es, mientras que el cable está bajo un imán,

$\ v_{s}=\Omega R \ell B_{r}$

Ahora bien, si los imanes tienen extensión angular$\ \theta_{m}$ el voltaje inducido en un cable tendrá una forma de onda como se muestra en la Figura 18: Es similar a pulso y tiene la misma forma que el campo magnético de los imanes.

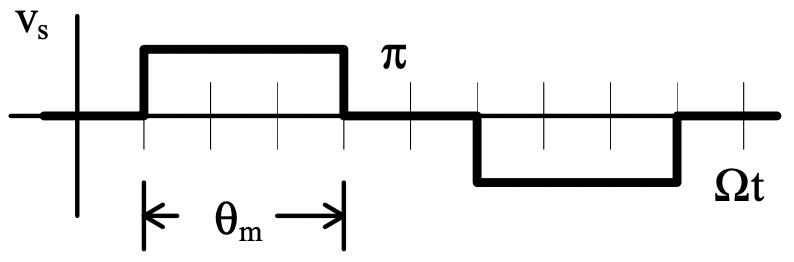Figura 18: Voltaje inducido en un conductor

El voltaje producido por una bobina en realidad se compone de dos formas de onda exactamente de esta forma, pero separadas en el tiempo por el ángulo de “lanzamiento de la bobina”. Entonces la forma de onda de voltaje total producida será la suma de las dos formas de onda. Si el ángulo de lanzamiento de la bobina es mayor que el ángulo del imán, las dos formas de onda de voltaje se suman para verse así: En realidad, hay dos formas de onda del lado de la bobina que se suman con un ligero desplazamiento de fase.

Si, por otro lado, la bobina lanzada es menor que el ángulo del imán, la imagen es la misma, solo el ancho de los pulsos es el de la bobina en lugar del imán. En cualquier caso, el voltaje promedio generado por una bobina es:

$\ v=\Omega R \ell N_{s} \frac{\theta^{*}}{\pi} B_{d}$

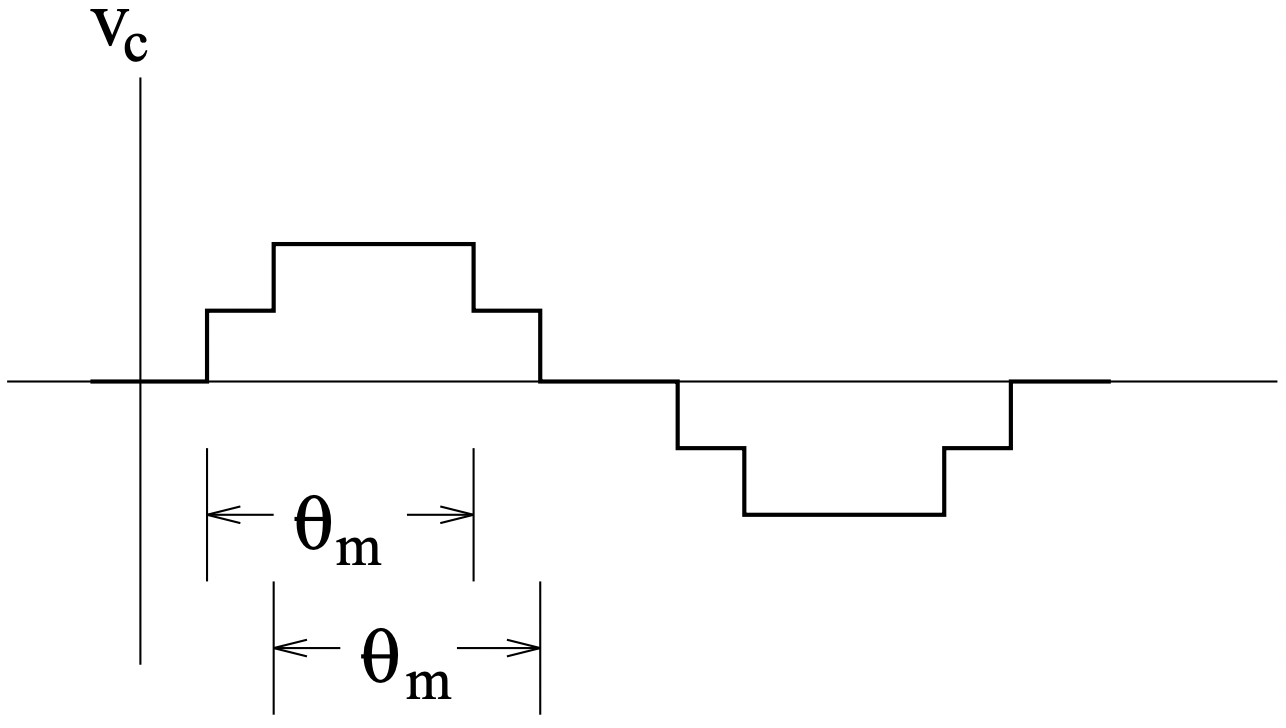Figura 19: Voltaje inducido en una bobina

donde$\ \theta^{*}$ es el menor de los ángulos de tiro de la bobina o imán y$\ N_{s}$ es el número de vueltas en serie en la bobina. Esto nos da la oportunidad de desarrollar el número de giros “activos”:

$\ \frac{C_{a}}{m}=N_{s} \frac{\theta^{*}}{\pi}=\frac{C_{\mathrm{tot}}}{m} \frac{\theta^{*}}{\pi}$

Aquí,$\ C_{a}$ es el número de conductores activos,$\ C_{\text {tot }}$ es el número total de conductores y$\ m$ es el número de trayectorias paralelas. El coeficiente motor es entonces:

$\ K=\frac{R \ell_{\mathrm{eff}} C_{\mathrm{tot}} B_{d}}{m} \frac{\theta^{*}}{\pi}$

Resistencia de la Armadura

El último elemento que necesitamos para la predicción de primer orden del rendimiento del motor es el valor de la resistencia de la armadura. La resistencia de la armadura está determinada simplemente por la longitud y el área del cable y por el número de trayectorias paralelas (generalmente igual a 2 para motores de conmutación pequeños). Si observamos$\ N_{c}$ como el número de bobinas y$\ N_{a}$ como el número de vueltas por bobina,

$\ N_{s}=\frac{N_{c} N_{a}}{m}$

La resistencia total de la armadura viene dada por:

$\ R_{a}=2 \rho_{w} \ell_{t} \frac{N_{s}}{m}$

donde$\ \rho_{w}$ es la resistividad (por unidad de longitud) del cable:

$\ \rho_{w}=\frac{1}{\frac{\pi}{4} d_{w}^{2} \sigma_{w}}$

($\ d_{w}$es el diámetro del alambre,$\ \sigma_{w}$ es la conductividad del cable y$\ \ell_{t}$ es la longitud de media vuelta). Esta longitud depende de cómo se enrolle la máquina, pero una buena suposición de primer orden podría ser algo como esto:

$\ \ell_{t} \approx \ell+\pi R$