2.3: Ecuaciones de Bloch
- Page ID
- 84826
Los átomos en baja concentración muestran espectros lineales tal como se encuentran en medios láser de gas, tinte y algunos de estado sólido. Por lo general, hay infinitamente muchos autoestados de energía en un medio atómico, molecular o de estado sólido y las líneas espectrales están asociadas con transiciones permitidas entre dos de estos autoestados de energía. Por muchas consideraciones físicas ya es suficiente tomar en cuenta sólo dos de los posibles estados propios de energía, por ejemplo los que están relacionados con la transición láser. El bombeo del láser puede describirse mediante procesos de relajación fenomenológica hacia el nivel láser superior y fuera del nivel láser inferior. El modelo simple resultante a menudo se denomina átomo de dos niveles, que matemáticamente también es equivalente a una partícula de espín 1/2 en un campo magnético externo, porque el espín solo puede ser paralelo o antiparalelo al campo, es decir, tiene dos niveles de energía y autoestados de energía. La interacción del átomo de dos niveles o el espín con el campo eléctrico o magnético es descrita por las ecuaciones de Bloch.
Modelo de dos niveles
Un átomo que tiene solo dos valores propios de energía es descrito por un espacio de estado bidimensional abarcado por los dos estados propios de energía |\(e\)\ rangle y |\(g\)\ rangle. Los dos estados constituyen un sistema ortonormal completo. Los valores propios de energía correspondientes son\(E_e\) y\(E_g\) (Figura 2.2).
En la representación de posición, es decir, x, estos estados corresponden a las funciones de onda
\[\psi_e(x) = \langle x|e \rangle , \ \ \ \ \ \text{ and } \psi_g(x) = \langle x|g \rangle .\label{eq2.3.1} \]
El hamiltoniano del átomo viene dado por
\[H_A = E_e |e\rangle \langle e| + E_g |g\rangle \langle g|. \nonumber \]
En este espacio de estado bidimensional solo son posibles operadores lineales\(2 \times 2 = 4\) linealmente independientes. Una posible elección para una base de operador en este espacio es
\[1 = |e \rangle \langle e| + |g\rangle \langle g|, \nonumber \]
\[\sigma_z = |e\rangle \langle e| - |g\rangle \langle g|,\label{eq2.3.4} \]
\[\sigma^+ = |e\rangle \langle g|, \nonumber \]
\[\sigma^- = |g\rangle \langle e|.\label{eq2.3.6} \]
Los operadores no hermitianos\(\sigma^{\pm}\) podrían ser reemplazados por los operadores hermitianos\(\sigma_{x,y}\)
\[\sigma_x = \sigma^+ + \sigma^-, \nonumber \]
\[\sigma_y = -j\sigma^+ + j\sigma^-. \nonumber \]
El significado físico de estos operadores se vuelve obvio, si miramos la acción cuando se aplica a un estado arbitrario
\[|\psi \rangle = c_g |g \rangle + c_e| e\rangle .\label{eq2.3.9} \]
Obtenemos
\[\sigma^+|\psi \rangle = c_g|e\rangle , \nonumber \]
\[\sigma^-|\psi \rangle = c_e|g\rangle , \nonumber \]
\[\sigma_z|\psi \rangle = c_e|e\rangle -c_g |g\rangle . \nonumber \]
El operador\(\sigma^+\) genera una transición del suelo al estado excitado, y\(\sigma^-\) hace lo contrario. En contraste con\(\sigma^+\) y\(\sigma^-\),\(\sigma_z\) es un operador hermitiano, y su valor de expectativa es una cantidad física observable con valor de expectativa
\[\langle \psi |\sigma_z| \psi \rangle = |c_e|^2 - |c_g|^2 = \omega, \nonumber \]
la inversión\(\omega\) del átomo, ya que\(|c_e|^2\) y\(|c_g|^2\) son las probabilidades de encontrar el átomo en estado\(|e \rangle \) o\(|g \rangle \) sobre una medición correspondiente.
Si consideramos un conjunto de\(N\) átomos la inversión total sería\(\sigma = N\langle \psi |\sigma_z| \psi \rangle \). Si separamos del hamiltoniano (Ecuación\(\ref{eq2.3.1}\)) el término\((E_e + E_g)/2 \cdot 1\), donde 1 denota la matriz de unidad, reescalamos los valores de energía correspondientemente y obtenemos para el hamiltoniano del sistema de dos niveles
\[H_A = \dfrac{1}{2} \hat{h} \omega_{eg} \sigma_z, \nonumber \]
con la frecuencia de transición
\[\omega_{eg} = \dfrac{1}{\hat{h}} (E_e - E_g). \nonumber \]
Esta forma del hamiltoniano es favorable. Existen las siguientes relaciones de conmutador entre operadores (Ecuación\(\ref{eq2.3.4}\)) a (Ecuación\(\ref{eq2.3.6}\))
\[[\sigma^+, \sigma^-] = \sigma_z,\label{eq2.3.16} \]
\[[\sigma^+, \sigma_z] = -2\sigma^+, \nonumber \]
\[[\sigma^-, \sigma_z] = 2\sigma^-,\label{eq2.3.18} \]
y relaciones anti-conmutador, respectivamente
\[[\sigma^+, \sigma^-]_+ = 1, \nonumber \]
\[[\sigma^+, \sigma_z]_+ = 0, \nonumber \]
\[[\sigma^-, \sigma_z]_+ = 0, \nonumber \]
\[[\sigma^-, \sigma^-]_+ = [\sigma^+, \sigma^+]_+ = 0, \nonumber \]
Los operadores\(\sigma_x\),\(\sigma_y\),\(\sigma_z\) cumplen con las relaciones de conmutador de momento angular
\[[\sigma_x, \sigma_y] = 2j \sigma_z, \nonumber \]
\[[\sigma_y, \sigma_z] = 2j \sigma_x, \nonumber \]
\[[\sigma_z, \sigma_x] = 2j \sigma_y, \nonumber \]
El espacio de estado bidimensional se puede representar como vectores de\(\mathbb{C}^2\) acuerdo con la regla:
\[|\psi \rangle = c_e| e\rangle + c_g|g \rangle \to \ \ \left (\begin{matrix} c_e \\ c_g \end{matrix} \right ). \nonumber \]
Los operadores son entonces representados por matrices
\[\sigma^+ \to \left ( \begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix} \right ),\label{eq2.3.27} \]
\[\sigma^- \to \left ( \begin{matrix} 0 & 0 \\ 1 & 0 \end{matrix} \right ), \nonumber \]
\[\sigma_z \to \left ( \begin{matrix} 1 & 0 \\ 0 & -1 \end{matrix} \right ), \nonumber \]
\[1 \to \left ( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right ).\label{eq.2.3.30} \]
Interacción Atom-Campo en Aproximación de Dipolos
El momento dipolar de un átomo\(\tilde{P}\) está determinado esencialmente por el operador de posición\(\vec{x}\) a través de
\[\vec{P} = -e_0 \vec{x}.\label{eq2.3.31} \]
Entonces el valor de expectativa para el momento dipolar de un átomo en estado (Ecuación\(\ref{eq2.3.9}\)) es
\[\begin{array} {rcl} {\langle \psi |\vec{P}|\psi \rangle } & = & {-e_0 (|c_e|^2 \langle e|\bar{x}|e \rangle + c_e c_g^* \langle g|\bar{x}| e\rangle } \\ {} & + & {c_gc_e^* \langle e|\bar{x}| g\rangle +|c_g|^2 \langle g|\bar{x}|g \rangle ).}\end{array} \nonumber \]
Por simplicidad, podemos suponer que ese medio es un gas atómico. Los átomos poseen simetría de inversión, por lo tanto, los autoestados energéticos deben ser simétricos o antisimétricos, es decir\(\langle e|\bar{x}|e\rangle =\langle g|\bar{x}|g\rangle =0\). Obtenemos
\[\langle \psi |\bar{P} \psi\rangle = -e_0 (c_ec_g^* \langle g|\bar{x}|e\rangle + c_g c_e^* \langle g|\bar{x}|e\rangle ^*). \nonumber \]
(Nota, esto quiere decir, no hay momento dipolar permanente en un átomo, que está en un estado propio de energía. Tenga en cuenta que este podría no ser el caso en un sólido. Los átomos que constituyen el sólido están orientados en una red, lo que puede romper la simetría. Si es así, hay momentos dipolares permanentes y consecuentemente los elementos de la matriz\(\langle e|\bar{x}|e \rangle \) y no\(\langle g|\bar{x}|g \rangle \) desaparecerían. Si es así, también hay campos de cristal, que luego implican cambios de nivel, a través del efecto Stark lineal). Así un átomo solo exhibe un momento dipolar en la media, si el producto\(c_ec_g^* \ne 0\), es decir, el estado del átomo está en una superposición de estados\(|e \rangle \) y\(|g \rangle \).
Con los elementos de la matriz dipolo
\[\bar{M} = e_0 \langle g|\bar{x}|e\rangle \nonumber \]
el valor de expectativa para el momento dipolo se puede escribir como
\[\langle \psi |\bar{P}| \psi \rangle = -(c_e c_g^* \vec{M} + c_g c_e^* \vec{M}^*) = - \langle \psi |(\sigma^+ \vec{M}^* + \sigma^- \vec{M})|\psi \rangle . \nonumber \]
Como esto es cierto para un estado arbitrario, el operador dipolo (Ecuación\(\ref{eq2.3.31}\)) está representado por
\[\vec{P} = \vec{P}^+ + \vec{P}^- = -\vec{M}^* \sigma^+ - \vec{M} \sigma^-.\label{eq2.3.36} \]
Por lo tanto, los operadores\(\sigma^+\) y\(\sigma^-\) son proporcionales a los operadores de momento dipolo complejo\(\vec{P}^+\) y\(\vec{P}^-\), respectivamente.
La energía de un dipolo eléctrico en un campo eléctrico es
\[H_{A - F} = -\vec{P} \cdot \vec{E} (\vec{x}_A, t). \nonumber \]
El campo eléctrico en la posición del átomo,\(\vec{x}_A\), puede escribirse como
\[\vec{E} (\vec{x}_A, t) = \dfrac{1}{2} \left (\vec{E} (t)^{(+)} + \vec{E} (t)^{(-)} \right ) =\dfrac{1}{2} \left (\hat{\vec{E}} (t)^{(+)} e^{j\omega t} + \hat{\vec{E}} (t)^{(-)} e^{-j\omega t}\right ), \nonumber \]
donde\(\hat{\vec{E}} (t)^{(+)}\) denota la envolvente de campo complejo que varía lentamente con\(\omega \approx \omega_{eg}\). En la Aproximación de Onda Rotatoria (RWA), solo mantenemos los componentes que varían lentamente en la interacción hamiltoniana. Como veremos más adelante, si no hay campo el operador\(\sigma^+\) evoluciona como\(\sigma^+ (t) = \sigma^+ (0) e^{j \omega_{eg} t}\), así obtenemos en RWA
\[H_{A-F} = -\vec{P} \cdot \vec{E} (\vec{x}_A, t) \approx \nonumber \]
\[\approx H_{A-F}^{RWA} =\dfrac{1}{2} \vec{M}^* \vec{E} (t)^{(-)} \sigma^+ + h.c.. \nonumber \]
La ecuación de Schrödinger para el átomo de dos niveles en un campo clásico viene dada entonces por
\[jh\dfrac{d}{dt} |\psi \rangle = (H_A + H_{A- F}|\psi \rangle \nonumber \]
\[\approx (H_A + H_{A - F}^{RWA})|\psi \rangle . \nonumber \]
Escrito en la representación energética, obtenemos
\[\dfrac{d}{dt} c_e = -j\dfrac{\omega_{eg}}{2} c_e - j \Omega_r e^{-j\omega t} c_g,\label{eq2.3.43} \]
\[\dfrac{d}{dt} c_g = +j\dfrac{\omega_{eg}}{2} c_g - j \Omega_r e^{+j\omega t} c_e,\label{eq2.3.44} \]
con la frecuencia RABI definida como
\[\Omega_r = \dfrac{\vec{M}^* \hat{\vec{E}}}{2\hbar}. \nonumber \]
Por el momento, suponemos que la frecuencia Rabi-frecuencia es real. De no ser así,\(c_{a,b}\) sería necesaria una transformación que incluyera un cambio de fase en las amplitudes para eliminar esta fase. Como era de esperar el campo empareja a los autoestados energéticos.
Oscilaciones rabi-
Si la luz incidente tiene una amplitud de campo constante\(\hat{\vec{E}}\) Eqs. (\(\ref{eq2.3.43}\)) y (\(\ref{eq2.3.44}\)) pueden resolverse y observamos una oscilación en la diferencia poblacional, la Rabi-oscilación [1]. Para mostrar esto se introduce la desintonización entre campo y resonancia atómica
\[\Delta = \dfrac{\omega_{ab} - \omega}{2} \nonumber \]
y las nuevas amplitudes de probabilidad
\[C_e = c_e e^{j \tfrac{\omega}{2} t}, \nonumber \]
\[C_g = c_g e^{-j \tfrac{\omega}{2} t}, \nonumber \]
Esto lleva al nuevo sistema de ecuaciones con coeficientes constantes
\[\dfrac{d}{dt} C_e = -j\Delta C_e - j \Omega_r C_g, \nonumber \]
\[\dfrac{d}{dt} C_g = +j\Delta C_g - j \Omega_r C_e, \nonumber \]
Tenga en cuenta que estos son el acoplamiento de ecuaciones de modo en el tiempo. Ahora bien, los modos son electrónicos en lugar de modos fotónicos. Pero por lo demás todo es igual. Para el caso de la desaparición de la desintonización es especialmente fácil eliminar una de las variables y llegamos a
\[\dfrac{d^2}{dt^2} C_e = -\Omega_r^2 C_e \nonumber \]
\[\dfrac{d^2}{dt^2} C_g = -\Omega_r^2 C_g \nonumber \]
La solución a este conjunto de ecuaciones son las oscilaciones que estamos buscando. Si el átomo está en el momento\(t = 0\) en el estado fundamental, es decir\(C_e (0) = 0\),\(C_g (0) = 1\) y, respectivamente, llegamos a
\[|c_b (t)|^2 = \cos^2 (\Omega, t) \nonumber \]
\[|c_a (t)|^2 = \sin^2 (\Omega, t) \nonumber \]
Entonces, las probabilidades de encontrar el átomo en el suelo o estado excitado son
\[\langle \vec{P}\rangle = -\vec{M} c_e c_g^* + c.c. \nonumber \]
\[=-\vec{M} \sin (2\Omega_r t)\sin (\omega_{eg} t).\label{eq2.3.56} \]
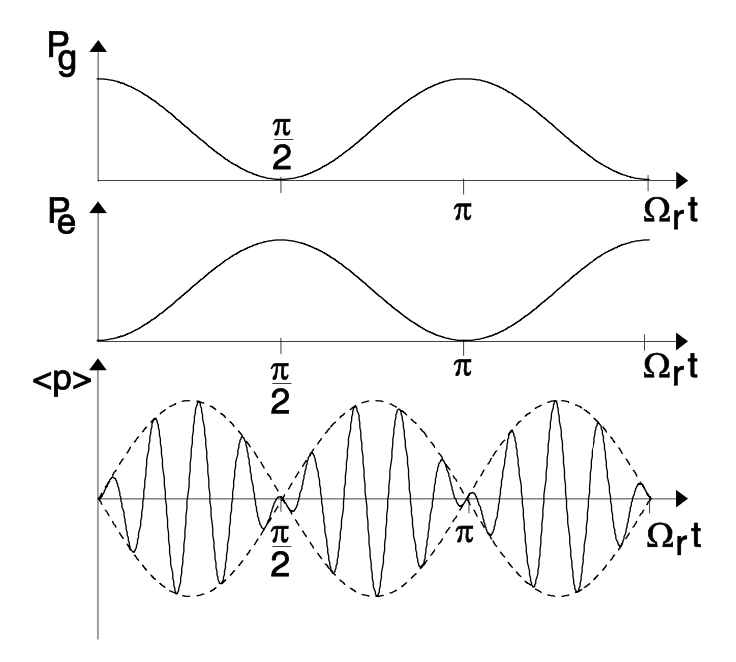
El campo externo coherente impulsa la población del sistema atómico entre los dos estados disponibles con un periodo\(T_r = \pi/\Omega_r\). Aplicar el campo sólo más de la mitad de este periodo conduce a una inversión completa de la población. Estas oscilaciones rabi-se han observado en diversos sistemas que van desde gases hasta semiconductores. Curiosamente, la luz emitida desde el átomo de dos niveles impulsado coherentemente no es idéntica en frecuencia al campo de conducción. Si nos fijamos en el espectro de Fourier de la polarización de acuerdo con la Ec. (\(\ref{eq2.3.56}\)), obtenemos líneas a frecuencias\(\omega_{\pm} = \omega_{eg} \pm 2 \Omega_r\). Esto es claramente una salida no lineal y las bandas laterales se llaman Mollow-sidebands [2]. Lo más importante para la existencia de estas oscilaciones es la coherencia del sistema atómico sobre al menos una oscilación RABI. Si esta coherencia se destruye lo suficientemente rápido, las oscilaciones Rabi-oscilaciones no pueden ocurrir y entonces es imposible generar inversión en un sistema de dos niveles por interacción con la luz. Este es el caso de una gran clase de situaciones en la interacción luz-materia. Por lo que nos interesa lo que sucede en el caso de pérdida de coherencia debido a la interacción adicional de los átomos con un baño de calor.
Operador de Densidad
Para estudiar procesos incoherentes o disipativos es útil cambiar a una descripción estatística utilizando el operador de densidad en lugar de funciones de onda deterministas similares a la mecánica estadística clásica, donde las trayectorias deterministas de las partículas son reemplazadas por distribuciones de probabilidad.
El operador de densidad de un estado puro se define por el producto diádico del estado consigo mismo
\[\rho = |\psi \rangle \langle \psi| \nonumber \]
o en representación de coordenadas por una\(2 \times 2\) −matrix
\[\rho = \left ( \begin{matrix} \rho_{ee} & \rho_{eg} \\ \rho_{ge} & \rho_{gg} \end{matrix} \right ). \nonumber \]
En caso de un estado puro (\(\ref{eq2.3.9}\)) esto es
\[\rho = \left ( \begin{matrix} c_ec_e^* & c_ec_g^* \\ c_gc_e^* & c_gc_g^* \end{matrix} \right ). \nonumber \]
Es obvio, que, para el caso bastante sencillo de un sistema de dos niveles, cada elemento de la matriz de densidad corresponde a una cantidad física. La diagonal principal contiene las probabilidades poblacionales para los niveles y el elemento fuera de la diagonal es el valor de expectativa de la componente de frecuencia positiva o negativa del momento dipolar del átomo, es decir, su contribución a la polarización media.
El valor de expectativa de un operador arbitrario se\(A\) puede calcular usando la fórmula de traza
\[\langle A \rangle = Tr\{\rho A\} =\langle \psi |A| \psi \rangle . \nonumber \]
La ventaja del operador de densidad es que las mezclas de estados puros también pueden tratarse en un sentido estadístico. Por ejemplo, si el átomo está en estado\(|e \rangle \) con probabilidad\(p_e\) y en estado\(|g \rangle \) con probabilidad\(p_g\) un operador de densidad
\[\rho = p_e|e\rangle \langle e|+p_g|g\rangle \langle g| \nonumber \]
, que se puede utilizar para calcular los valores promedio de observables en el sentido estadístico adecuado
\[\langle A\rangle =T_r \{\rho A\} = p_e\langle e|A|e\rangle +p_g \langle g|A|g\rangle . \nonumber \]
Dado que las matrices (\(\ref{eq2.3.27}\)) a (\(\ref{eq2.3.30}\)) construyen una base completa en el espacio de\(2 \times 2\) −matrices, podemos expresar la matriz de densidad como
\[\rho = \rho_{ee} \dfrac{1}{2} (1 + \sigma_z) + \rho_{gg} \dfrac{1}{2} (1 - \sigma_z) + \rho_{eg} \sigma^+ + \rho_{ge} \sigma^- \nonumber \]
\[=\dfrac{1}{2} 1 + \dfrac{1}{2} (\rho_{ee} -\rho_{gg}) \sigma_z + \rho_{eg} \sigma^+ + \rho_{ge} \sigma^-, \nonumber \]
ya que el rastro de la matriz de densidad es siempre uno (normalización). Eligiendo la nueva base\(1, \sigma_x, \sigma_y, \sigma_z\), obtenemos
\[\rho = \dfrac{1}{2} 1 + \dfrac{1}{2} (\rho_{ee} - \rho_{gg})\sigma_z + d_x \sigma_x + d_y \sigma_y, \nonumber \]
con
\[d_x = \dfrac{1}{2} (\rho_{eg} + \rho_{ge}) = \Re\{\langle \sigma^{(+)} \rangle \}, \nonumber \]
\[d_y = \dfrac{j}{2} (\rho_{eg} - \rho_{ge}) = \Im\{\langle \sigma^{(+)} \rangle \}, \nonumber \]
El valor de expectativa del operador dipolo viene dado por (\(\ref{eq2.3.36}\))
\[\langle \vec{P}\rangle =T_r \{\rho \vec{P}\} = -\vec{M}^* Tr\{\rho \sigma^+\} + c.c. = -\vec{M}^* \rho_{ge} + c.c. \nonumber \]
De la ecuación de Schrödinger para la función de onda\(|\psi \rangle \) podemos derivar fácilmente la ecuación de movimiento para el operador de densidad, llamada ecuación de von Neumann
\[\dot{\rho} = \dfrac{d}{dt} |\psi \rangle \langle \psi| + h.c. = \dfrac{1}{j\hbar} H|\psi \rangle \langle \psi| - \dfrac{1}{j\hbar} |\psi \rangle \langle \psi| H = \dfrac{1}{j\hbar} [H, \rho]. \nonumber \]
Debido a la naturaleza lineal de la ecuación, esta es también la ecuación correcta para un operador de densidad que describe una mezcla arbitraria de estados. En el caso de un átomo de dos niveles, la ecuación de von Neumann es
\[\dot{\rho} = \dfrac{1}{j\hbar} [H_A, \rho] = -j \dfrac{\omega_{\in g}}{2} [\sigma_z, \rho]. \nonumber \]
Usando las relaciones de conmutador (\(\ref{eq2.3.16}\)) - (\(\ref{eq2.3.18}\)), el resultado es
\[\dot{\rho}_{\in e} = 0,\label{eq2.3.71} \]
\[\dot{\rho}_{gg} = 0, \nonumber \]
\[\dot{\rho}_{eg} = -j \omega_{eg} \rho_{eg} \to \rho_{eg} (t) = e^{-j \omega_{eg} t} \rho_{eg} (0), \nonumber \]
\[\dot{\rho}_{ge} = j \omega_{eg} \rho_{ge} \to \rho_{ge} (t) = e^{j \omega_{eg} t} \rho_{ge} (0).\label{eq2.3.74} \]
Nuevamente el átomo aislado de dos niveles tiene una dinámica bastante simple, las poblaciones son constantes, solo el momento dipolar oscila con la frecuencia de transición\(\omega_{\in g}\), si ha habido un momento dipolar inducido en\(t = 0\), es decir, el sistema se encuentra en un estado de superposición.
Relajación Energética y de Fase
En realidad, no hay un átomo aislado. De hecho en nuestro caso nos interesa un átomo radiante, es decir, tiene una interacción dipolo con el campo. El acoplamiento con los infinitamente muchos modos del campo libre conduce ya a la emisión espontánea, un proceso irreversible. Podríamos tratar este proceso usando el Hamiltonian
\[H = H_A + H_F + H_{A-F}. \nonumber \]
Aquí,\(H_A\) es el hamiltoniano del átomo, HF del campo libre y\(H_{A-F}\) describe la interacción entre ellos. Un tratamiento completo en esta línea está más allá del alcance de esta clase y generalmente se realiza en clases de Mecánica Cuántica. Pero el resultado de este cálculo es simple y conduce en la ecuación de von Neumann de la matriz de densidad reducida, es decir, la matriz de densidad del átomo. Con la tasa de emisión espontánea\(1/\tau_{sp}\), es decir, el tiempo de vida espontáneo inverso\(\tau_{sp}\), las poblaciones cambian según
\[\dfrac{d}{dt} |c_e (t)|^2 = \dfrac{d}{dt} \rho_{ee} = -\Gamma_e \rho_{ee} + \Gamma_a \rho_{gg} \nonumber \]
con las abreviaturas
\[\Gamma_e = \dfrac{1}{\tau_{sp}} (n_{th} + 1), \nonumber \]
\[\Gamma_a = \dfrac{1}{\tau_{sp}} n_{th}.\label{eq2.3.78} \]
Aquí,\(n_{th}\) está el número de fotones térmicamente excitados en los modos del campo libre con frecuencia\(\omega_{eg}\),\(n_{th} = 1/(\exp (h\omega_{eg} /kT) - 1)\), a temperatura\(T\).
Se tiene que mantener la probabilidad total de estar en estado excitado o fundamental, es decir
\[\dfrac{d}{dt} \rho_{gg} = -\dfrac{d}{dt} \rho_{ee} = \Gamma_e \rho_{ee} - \Gamma_a \rho_{gg}.\label{eq2.3.79} \]
Si las poblaciones decaen, también lo hace la polarización, ya que\(\rho_{ge} = c_e^* c_g\), i.e.
\[\dfrac{d}{dt} \rho_{ge} j \omega_{eg} \rho_{eg} - \dfrac{\Gamma_e + \Gamma_a}{2} \rho_{ge}.\label{eq2.3.80} \]
Por lo tanto, los procesos de absorción y emisión también son destructivos para la fase, por lo tanto, las tasas correspondientes se suman en la tasa de decaimiento de fase.
Teniendo en cuenta los procesos coherentes (\(\ref{eq2.3.71}\)-\(\ref{eq2.3.74}\)) e incoherentes (\(\ref{eq2.3.79}\)-\(\ref{eq2.3.80}\)) se obtienen las siguientes ecuaciones para el momento dipolo promedio normalizado\(d = d_x + jd_y\) y la inversión\(w\)
\[\dot{d} = \dot{\rho}_{ge} = (j \omega_{eg} - \dfrac{1}{T_2})d,\label{eq2.3.81} \]
\[\dot{\omega} = \dot{\rho}_{ee} - \dot{\rho}_{gg} = \dfrac{\omega - \omega_0}{T_1},\label{eq2.3.82} \]
con las constantes de tiempo
\[\dfrac{1}{T_1} = \dfrac{2}{T_2} = \Gamma_e + \Gamma_a = \dfrac{2n_{th} + 1}{\tau_{sp}} \nonumber \]
e inversión de equilibrio\(w_0\), debido a la excitación térmica del átomo por el campo térmico
\[w_0 = \dfrac{\Gamma_a - \Gamma_e}{\Gamma_a + \Gamma_e} = \dfrac{-1}{1 + 2n_{th}} = -\tanh \left (\dfrac{\hbar\omega_{eg}}{2kT} \right ).\label{eq2.3.84} \]
La constante de tiempo\(T_1\) denota la relajación energética en el sistema de dos niveles y\(T_2\) la relajación de fase. \(T_2\)es el tiempo de correlación entre amplitudes\(c_e\) y\(c_g\). Esta coherencia es destruida por la interacción del sistema de dos niveles con el entorno. En este modelo la relajación energética es la mitad de la tasa de relajación de fase o
\[T_2 = 2T_1 \nonumber \]
Los átomos en un medio láser no sólo interactúan con el campo electromagnético, sino que además también con los fonones de la red huésped, podrían colisionar entre sí en un láser de gas y así sucesivamente. Todos estos procesos deben ser considerados a la hora de determinar las tasas de energía y relajación de fase. Algunos de estos procesos sólo están destruyendo la fase, pero en realidad no conducen a una pérdida de energía en el sistema. Por lo tanto, estos procesos reducen\(T_2\) pero no tienen influencia en\(T_1\). En sistemas reales, el tiempo de relajación de fase suele ser mucho más corto que el doble del tiempo de relajación energética,
\[T_2 \le 2 T_1. \nonumber \]
Si la inversión se desvía de su valor de equilibrio\(w_0\), se relaja de nuevo al equilibrio con una constante de tiempo\(T_1\). La ecuación (\(\ref{eq2.3.84}\)) muestra que para todas las temperaturas\(T \rangle 0\) la inversión es negativa, es decir, el nivel inferior está más poblado que el nivel superior. Por lo tanto, no se puede lograr la inversión incoherente de la luz térmica en un sistema de dos niveles. La inversión solo se puede lograr bombeando con luz incoherente, si hay más niveles y procesos de relajación posteriores hacia el nivel láser superior. Debido a estos procesos de relajación, la tasa\(\Gamma_a\) se desvía de la expresión de equilibrio (\(\ref{eq2.3.78}\)), y tiene que ser reemplazada por la velocidad de bombeo\(\Lambda\). Si la tasa de bombeo\(\Lambda\) excede\(\Gamma_e\), la inversión correspondiente a la Ecuación (\(\ref{eq2.3.84}\)) se vuelve positiva,
\[w_0 = \dfrac{\Lambda - \Gamma_e}{\Lambda + \Gamma_e}. \nonumber \]
Si permitimos temperaturas negativas artificiales, obtenemos con\(T \langle 0\) para la relación de tasas de relajación
\[\dfrac{\Gamma_e}{\Gamma_a} = \dfrac{1+\bar{n}}{\bar{n}} = e^{\tfrac{\hbar \omega_{eg}}{kT}} \langle 1. \nonumber \]
De esta manera, el bombeo del sistema de dos niveles aleja al sistema del equilibrio térmico, lo que tiene que esperarse.
Átomo de dos niveles con un campo externo clásico coherente
Si hay además del acoplamiento a un baño de calor externo, que modela la descomposición espontánea, bombeo y otros procesos incoherentes, un campo externo coherente, el hamiltoniano tiene que ser extendido por la interacción dipolo con ese campo,
\[H_E = -\vec{P} \vec{E} (\vec{x}_A, t). \nonumber \]
Nuevamente utilizamos la interacción hamiltoniana en RWA
\[H_E = \dfrac{1}{2} \vec{M}^* \vec{E} (t)^{(-)} \sigma^+ + h.c.. \nonumber \]
Esto lleva en la ecuación de von Neumann al término adicional
\[\dot{\rho} |_E = \dfrac{1}{j\hbar} [H_E, \rho] \nonumber \]
\[= \dfrac{1}{2j\hbar} \vec{M}^* \vec{E} (t)^{(-)} [\sigma^+, \rho] + h.c. \nonumber \]
o
\[\rho{\rho}_{ee}|_E = \dfrac{1}{2j\hbar} \vec{E}^{(-)} \rho_{ge} + c.c., \nonumber \]
\[\rho{\rho}_{ge}|_E = \dfrac{1}{2j\hbar} \vec{E}^{(+)} (\rho_{ee} -\rho_{gg}), \nonumber \]
\[\rho{\rho}_{gg}|_E = -\dfrac{1}{2j\hbar} \vec{E}^{(-)} \rho_{ge} + c.c., \nonumber \]
La evolución del momento dipolo y la inversión se cambia por
\[\dot{d}|_E = \dot{\rho}_{ge}|_E = \dfrac{1}{2j\hbar} \vec{M} \vec{E}^{(+)} w, \nonumber \]
\[\dot{w}|_E = \dot{\rho}_{ee}|_E - \dot{\rho}_{gg}|_E = \dfrac{1}{j\hbar} (\vec{M}^* \vec{E}^{(-)} d^* - \vec{M} \vec{E}^{(+)} d). \nonumber \]
Así, la dinámica total del sistema de dos niveles incluyendo los procesos de bombeo y desfase de Eqs. (\(\ref{eq2.3.81}\)) y (\(\ref{eq2.3.82}\)) viene dada por
\[\dot{d} = -(\dfrac{1}{T_2} - j \omega_{eg})d + \dfrac{1}{2j \hbar} \vec{M} \vec{E}^{(+)} w, \nonumber \]
\[\dot{w} = -\dfrac{w-w_0}{T_1} + \dfrac{1}{j\hbar} (\vec{M}^* \vec{E}^{(-)} d - \vec{M} \vec{E}^{(+)} d^*). \nonumber \]
Estas ecuaciones se denominan ecuaciones de Bloch. Describen la dinámica de un átomo que interactúa con un campo eléctrico clásico. Junto con la Ecuación (2.2.2) construyen las ecuaciones de Maxwell-Bloch.