2.7: Relaciones Kramers-Kroenig

Última actualización
Guardar como PDF

Page ID: 84825

Franz X. Kaertner
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

La susceptibilidad lineal es la respuesta de frecuencia de un sistema lineal a un campo eléctrico aplicado, lo cual es causal, por lo que las partes reales e imaginarias obedecen a las Relaciones Kramers-Kroenig

\[\chi_r (\Omega) = \dfrac{2}{\pi} \int_{0}^{\infty} \dfrac{\omega \chi_i (\omega)}{\omega^2 - \Omega^2} d\omega = n^2 (\Omega) - 1, \nonumber \]

\[\chi_i (\Omega) = -\dfrac{2}{\pi} \int_{0}^{\infty} \dfrac{\Omega \chi_r (\omega)}{\omega^2 - \Omega^2} d\omega. \nonumber \]

En medios transparentes uno está operando lejos de las resonancias. Entonces la absorción o parte imaginaria de la susceptibilidad se puede aproximar por

\[\chi_i (\Omega) = \sum_i A_i \delta (\omega -\omega_i) \nonumber \]

y los resultados de la relación Kramers-Kroenig en una ecuación de Sellmeier para el índice de refracción

\[\begin{align*} n^2 (\Omega) &= 1 + \sum_i A_i \dfrac{\omega_i}{\omega_i^2 - \Omega^2} \\[4pt] &= 1 + \sum_i a_i \dfrac{\lambda}{\lambda^2 - \lambda_i^2} \end{align*} \nonumber \]

Para un ejemplo en el Cuadro 2.1 se muestran los coeficientes sellmeier para cuarzo fundido y zafiro.

Cuadro 2.1: Tabla con coeficientes de Sellmeier para cuarzo fundido y zafiro.
	Cuarzo Fundido	Zafiro
\(a_1\)	0.6961663	1.023798
\(a_2\)	0.4079426	1.058364
\(a_3\)	0.8974794	5.280792
\(\lambda_1^2\)	\(4.679148 \cdot 10^{-3}\)	\(3.77588 \cdot 10^{-3}\)
\(\lambda_2^2\)	\(1.3512063 \cdot 10^{-2}\)	\(1.22544 \cdot 10^{-2}\)
\(\lambda_3^2\)	\(0.9793400 \cdot 10^{2}\)	\(3.213616 \cdot 10^{2}\)

Una situación típica para un material que tiene resonancias en los rayos UV e IR, tal como vidrio, se muestra en la Figura 2.12

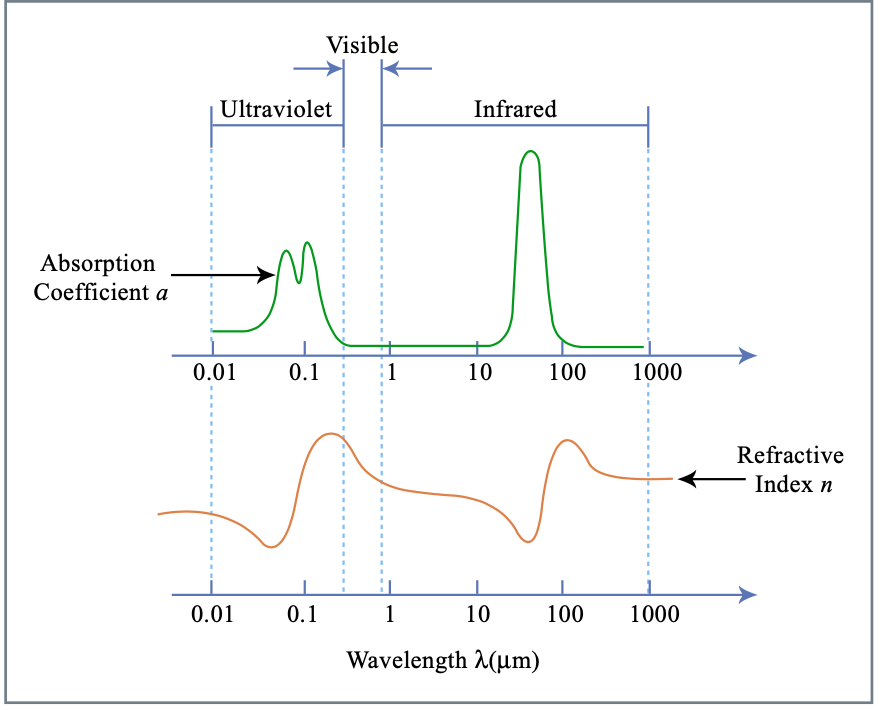
2021-04-06 11.36.18.png — Figura 2.12: Distribución típica de líneas de absorción en un medio transparente en lo visible. Figura por MIT OCW.

Las regiones donde el índice de refracción disminuye con la longitud de onda se suele llamar rango de dispersión normal y el comportamiento opuesto dispersión anormal

\[\begin{array} {rcl} {\dfrac{dn}{d\lambda}} & < & {\text{0: normal dispersion (blue refracts more than red)}} \\ {\dfrac{dn}{d\lambda}} & > & {\text{0: abnormal dispersion}} \end{array}\nonumber \]

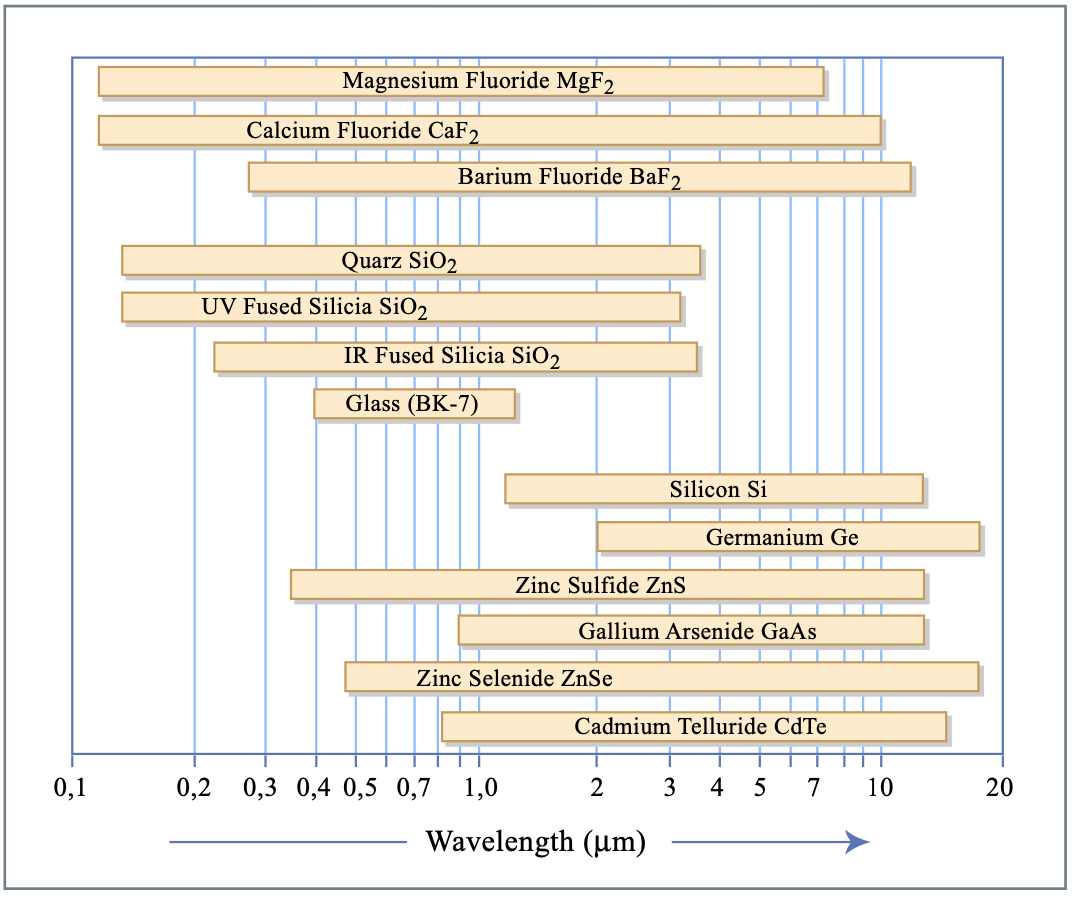
La Fig. 2.13 muestra el rango de transparencia de algunos medios de uso frecuente.

2021-04-06 11.39.45.png — Figura 2.13: Rango de transparencia de algunos materiales. Figura por MIT OCW.