4.1: Ecuaciones de velocidad

En la sección 2.5, derivamos para la interacción de un átomo de dos niveles con un campo láser propagando hacia la derecha las ecuaciones de movimiento (2.5.13) y (2.5.14), que se dan aquí nuevamente:

\[\left ( \dfrac{\partial}{\partial z} + \dfrac{1}{v_g} \dfrac{\partial}{\partial t} \right ) A(z, t) = \dfrac{N\hbar}{4T_2 E_s} w (z, t) A(z, t), \label{4.1.1} \]

\[\dot{w} = -\dfrac{w - w_0}{T_1} + \dfrac{|A(z,t)|^2}{E_s} w(z, t), \label{4.1.2} \]

donde\(T_1\) está la tasa de relajación de energía,\(v_g\) la velocidad de grupo en el material huésped donde están incrustados los dos átomos de nivel,\(E_s = I_sT_1\), la fluencia de saturación [\(J/cm^2\)], del medio.y\(I_s\) la intensidad de saturación de acuerdo con la Ecuación (2.4.7)

\[I_s = \left [\dfrac{2T_1T_2Z_F}{\hbar} \dfrac{|\vec{M} \hat{\vec{E}}|^2}{|\hat{\vec{E}}|^2} \right ]^{-1},\nonumber \]

que relaciona la intensidad de saturación con los parámetros microscópicos de la transición como las tasas de relajación longitudinal y transversal, así como el momento dipolar de la transición.

Figura 4.1: Ecuaciones de velocidad para el átomo de dos niveles

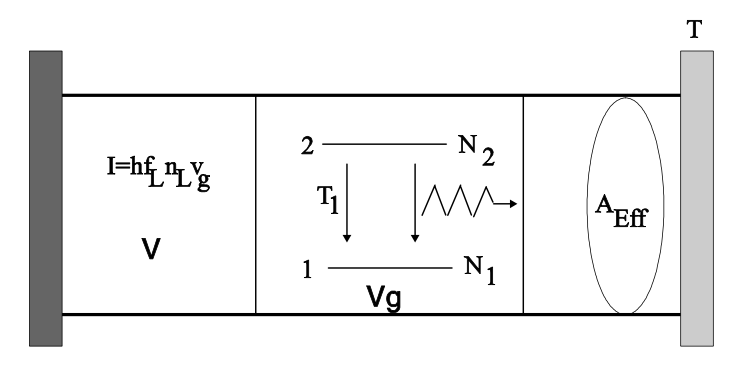
En muchos casos es más conveniente normalizar las Ecuaciones\ ref {4.1.1} y\ ref {4.1.2} a las poblaciones en nivel\(\text{e}\) y\(\text{g}\) o 2 y 1, respectivamente,\(N_2\) y\(N_1\), y la densidad de fotones,\(n_L\), en el modo interactuando con los átomos y viajando en el correspondiente velocidad de grupo, vg, ver Figura 4.1. La intensidad\(I\) en un modo que se propaga a velocidad de grupo\(v_g\) con un volumen de modo\(V\) está relacionada con el número de fotones\(N_L\) almacenados en el modo con volumen\(V\) por

\[I = hf_L \dfrac{N_L}{2^*V} v_g = \dfrac{1}{2^*} hf_Ln_Lv_g, \nonumber \]

donde\(hf_L\) está la energía fotónica. \(2^* = 2\)para un resonador láser lineal (entonces solo la mitad de los fotones van en una dirección), y\(2^* = 1\) para un láser de anillo. En este primer tratamiento consideramos el caso de ecuaciones de velocidad independientes del espacio, es decir, suponemos que el láser está oscilando en un solo modo y las densidades de energía de bombeo y modo son uniformes dentro del material láser. Con la sección transversal de interacción\(\sigma\) definida como

\[\sigma = \dfrac{hf_L}{2^*I_s T_1},\label{eq4.1.4} \]

y multiplicando la Ecuación (??) con el número de átomos en el modo, obtenemos

\[\dfrac{d}{dt} (N_2 - N_1) = -\dfrac{(N_2 - N_1)}{T_1} - \sigma (N_2 - N_1) v_g n_L + R_p \nonumber \]

Tenga en cuenta,\(v_gn_L\) es el flujo de fotones, por lo tanto σ es la sección transversal de emisión estimulada entre los átomos y los fotones. \(R_p\)es la velocidad de bombeo en el nivel superior del láser. Se puede derivar una ecuación de velocidad similar para la densidad de fotones

\[\dfrac{d}{dt} n_L = -\dfrac{n_L}{\tau_p} + \dfrac{l_g}{L} \dfrac{\sigma v_g}{V_g} [N_2 (n_L + 1) - N_1 n_L].\label{eq4.1.6} \]

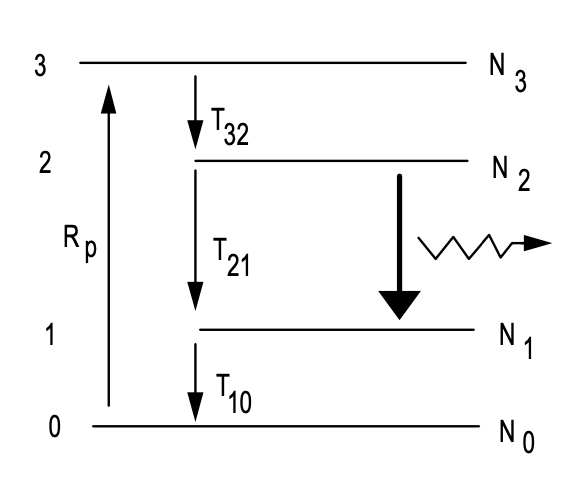
Aquí,\(\tau_p\) es la vida útil del fotón en la cavidad o tiempo de decaimiento de la cavidad y la de la Ec. (\(\ref{4.1.6}\)) da cuenta de la emisión espontánea que es equivalente a la emisión estimulada por un fotón que ocupa el modo. \(V_g\)es el volumen del medio de ganancia activa. Para una cavidad láser con un espejo semitransparente con transmisión\(T\), produciendo una pequeña pérdida de potencia\(2l = - \ln(1 - T) \approx T\) (para pequeñas\(T\)) por ida y vuelta en la cavidad, el tiempo de decaimiento de la cavidad\(T_R = 2^*L/c_0\) es\(\tau_p = 2l/T_R\), si es el tiempo de ida y vuelta en la cavidad lineal con longitud óptica\(2L\) o un anillo cavidad con longitud óptica\(L\). La longitud óptica\(L\) es la suma de la longitud óptica en el medio de ganancia\(n_{group} l_g\) y la longitud restante de la cavidad del espacio libre\(l_a\). Las pérdidas internas se pueden tratar de manera similar y contribuir al tiempo de decaimiento de la cavidad. Tenga en cuenta que la tasa de decaimiento para la inversión en ausencia de un campo,\(1/T_1\), no solo se debe a la emisión espontánea, sino que también es resultado de procesos de desintegración no radiativa. Véase por ejemplo el sistema de cuatro niveles que se muestra en la Figura 4.2. En el límite, donde las poblaciones en el tercer y primer nivel son cero, debido a las rápidas tasas de relajación\(T_{32}\), es decir\(T_{10} \to 0\), obtenemos

\[\dfrac{d}{dt} N_2 = -\dfrac{N_2}{\tau_L} - \sigma v_g N_2 n_L + R_p \nonumber \]

\[\dfrac{d}{dt} n_L = -\dfrac{n_L}{\tau_p} + \dfrac{l_g}{L} \dfrac{\sigma v_g}{V_g} N_2 (n_L + 1). \nonumber \]

Figura 4.2: Vier-Niveau-Laser

donde\(\tau_L = T_{21}\) es la vida útil del nivel láser superior. Experimentalmente, el número de fotones y la inversión en un resonador láser no son cantidades muy convenientes, por lo tanto, normalizamos ambas ecuaciones a la ganancia de amplitud de ida y vuelta\(g = \dfrac{l_g}{L} \dfrac{\sigma v_g}{2V_g} N_2 T_R\) experimentada por la luz y la potencia intracavitaria circulante\(P = I \cdot A_{eff}\)

\[\dfrac{d}{dt} g = -\dfrac{g-g_0}{\tau_L} - \dfrac{gP}{E_{sat}} \nonumber \]

\[\dfrac{d}{dt} P = -\dfrac{1}{\tau_p} P + \dfrac{2g}{T_R} (P + P_{vac}), \nonumber \]

con

\[E_s = I_s A_{eff} \tau_{L} = \dfrac{hf_L}{2^* \sigma} \nonumber \]

\[P_{sat} = E_{sat}/\tau_L \nonumber \]

\[P_{vac} = hf_L v_g/2^* L = hf_L/T_R \nonumber \]

\[g_0 = \dfrac{2^* v_g R_p}{2A_{eff} c_0} \sigma \tau_L,\label{eq4.1.14} \]

la pequeña señal de ganancia de ida y vuelta del láser. Tenga en cuenta que el factor de dos frente a ganancia y pérdida se debe al hecho, el\(g\) y\(l\) son ganancia y pérdida con respecto a la amplitud. La ecuación\ ref {eq4.1.14} aclara que la cifra de mérito que caracteriza a la pequeña ganancia de señal alcanzable con cierto material láser es el\(\sigma \tau_L\) -producto.

Cuadro 4.1: Rango de longitud de onda, sección transversal para emisión estimulada, vida útil del estado superior, ancho de línea, tipo de forma de línea (H = ensanchado homogéneamente, I = ensanchado inhomogéneamente) e índice para algunos materiales láser de estado sólido de uso frecuente, y en comparación con los láseres semiconductores y colorantes.

Medio Láser	Longitud de onda\(\lambda_0\) (\(n\)m)	Sección transversal\(\sigma\) (\(\text{cm}^2\))	Superior—St. Vida\(\tau_L\) (\(\mu\)s)	Linewidth\(\Delta f_{FWHM} = \tfrac{2}{T_2} (\text{THz})\)	Typ	Índice refr.\(n\)
\(\text{Nd}^{3+}: \ce{YAG}\)	\ (\ lambda_0\) (\(n\)m) ">1.064	\ (\ sigma\) (\(\text{cm}^2\)) ">\(4.1 \cdot 10^{-19}\)	\ (\ Tau_l\) (\(\mu\)s) ">1,200	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">0.210	H	\ (n\) ">1.82
\(\text{Nd}^{3+}: \ce{LSB}\)	\ (\ lambda_0\) (\(n\)m) ">1,062	\ (\ sigma\) (\(\text{cm}^2\)) ">\(1.3 \cdot 10^{-19}\)	\ (\ Tau_l\) (\(\mu\)s) ">87	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">1.2	H	\ (n\) ">1.47 (ne)
\(\text{Nd}^{3+}: \ce{YLF}\)	\ (\ lambda_0\) (\(n\)m) ">1.047	\ (\ sigma\) (\(\text{cm}^2\)) ">\(1.8 \cdot 10^{-19}\)	\ (\ Tau_l\) (\(\mu\)s) ">450	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">0.390	H	\ (n\) ">1.82 (ne)
\(\text{Nd}^{3+}: \ce{YVO4}\)	\ (\ lambda_0\) (\(n\)m) ">1.064	\ (\ sigma\) (\(\text{cm}^2\)) ">\(2.5 \cdot 10^{-19}\)	\ (\ Tau_l\) (\(\mu\)s) ">50	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">0.300	H	\ (n\) ">2.19 (ne)
\(\text{Nd}^{3+}: \ce{glass}\)	\ (\ lambda_0\) (\(n\)m) ">1.054	\ (\ sigma\) (\(\text{cm}^2\)) ">\(4 \cdot 10^{-20}\)	\ (\ Tau_l\) (\(\mu\)s) ">350	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">3	H/I	\ (n\) ">1.5
\(\text{Er}^{3+}: \ce{glass}\)	\ (\ lambda_0\) (\(n\)m) ">1,55	\ (\ sigma\) (\(\text{cm}^2\)) ">\(6 \cdot 10^{-21}\)	\ (\ Tau_l\) (\(\mu\)s) ">10,000	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">4	H/I	\ (n\) ">1.46
Ruby	\ (\ lambda_0\) (\(n\)m) ">694.3	\ (\ sigma\) (\(\text{cm}^2\)) ">\(2 \cdot 10^{-20}\)	\ (\ Tau_l\) (\(\mu\)s) ">1,000	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">0.06	H	\ (n\) ">1.76
\(\text{Ti}^{3+}: \ce{Al2O3}\)	\ (\ lambda_0\) (\(n\)m) ">660-1180	\ (\ sigma\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-19}\)	\ (\ Tau_l\) (\(\mu\)s) ">3	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">100	H	\ (n\) ">1.76
\(\text{Cr}^{3+}: \ce{LiSAF}\)	\ (\ lambda_0\) (\(n\)m) ">760-960	\ (\ sigma\) (\(\text{cm}^2\)) ">\(4.8 \cdot 10^{-20}\)	\ (\ Tau_l\) (\(\mu\)s) ">67	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">80	H	\ (n\) ">1.4
\(\text{Cr}^{3+}: \ce{LiCAF}\)	\ (\ lambda_0\) (\(n\)m) ">710-840	\ (\ sigma\) (\(\text{cm}^2\)) ">\(1.3 \cdot 10^{-20}\)	\ (\ Tau_l\) (\(\mu\)s) ">170	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">65	H	\ (n\) ">1.4
\(\text{Cr}^{3+}: \ce{LiSGAF}\)	\ (\ lambda_0\) (\(n\)m) ">740-930	\ (\ sigma\) (\(\text{cm}^2\)) ">\(3.3 \cdot 10^{-20}\)	\ (\ Tau_l\) (\(\mu\)s) ">88	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">80	H	\ (n\) ">14
He-Ne	\ (\ lambda_0\) (\(n\)m) ">632.8	\ (\ sigma\) (\(\text{cm}^2\)) ">\(1 \cdot 10^{-13}\)	\ (\ Tau_l\) (\(\mu\)s) ">0.7	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ text {THz})\) ">0.0015	I	\ (n\) ">~1
\(\ce{Ar+}\)	\ (\ lambda_0\) (\(n\)m) ">515	\ (\ sigma\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-12}\)	\ (\ Tau_l\) (\(\mu\)s) ">0.07	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ text {THz})\) ">0.0035	I	\ (n\) ">~1
\(\ce{CO2}\)	\ (\ lambda_0\) (\(n\)m) ">10.600	\ (\ sigma\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-18}\)	\ (\ Tau_l\) (\(\mu\)s) ">2.900.000	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">0.000060	H	\ (n\) ">~1
Rodaamin-6G	\ (\ lambda_0\) (\(n\)m) ">560-640	\ (\ sigma\) (\(\text{cm}^2\)) ">\(3 \cdot 10^{-16}\)	\ (\ Tau_l\) (\(\mu\)s) ">0.0033	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">5	H	\ (n\) ">1.33
semiconductores	\ (\ lambda_0\) (\(n\)m) ">450-30,000	\ (\ sigma\) (\(\text{cm}^2\)) ">~\(10^{-14}\)	\ (\ Tau_l\) (\(\mu\)s) ">~0.002	\ (\ Delta f_ {FWHM} =\ tfrac {2} {T_2} (\ texto {THz})\) ">25	H/I	\ (n\) ">3-4

Cuanto más grande sea este producto, mayor será la pequeña ganancia de señal (\(g_0\)) alcanzable con cierto material láser. Cuadro 4.1

De la Eq. (2.4.7) y (\(\ref{eq4.1.4}\)) encontramos la siguiente relación entre la sección transversal de interacción de una transición y sus parámetros microscópicos como ancho de línea, momento dipolo y tasa de relajación energética

\[\sigma = \dfrac{hf_L}{I_{sat} T_1} = \dfrac{2T_2}{\hbar^2 Z_F} \dfrac{|\vec{M} \hat{\vec{E}}|^2}{|\hat{\tilde{E}}|^2}.\nonumber \]

Esta ecuación nos dice que los materiales láser de banda ancha, naturalmente, muestran secciones transversales de ganancia más pequeñas, si el momento dipolo es el mismo.