4.4: Conmutación Q
- Page ID
- 84902
Imagen eliminada debido a restricciones de derechos de autor. Consulte: Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 4.5: Dinámica de ganancia y pérdida de un láser de conmutación Q activa.
La energía almacenada en el medio láser puede liberarse repentinamente aumentando el valor Q de la cavidad para que el láser alcance el umbral. Esto se puede hacer activamente, por ejemplo moviendo rápidamente uno de los espejos resonadores en su lugar o pasivamente colocando un absorbedor saturable en el resonador [1, 16]. Hellwarth fue el primero en sugerir este método solo un año después de la invención del láser. Como orientación aproximada para un láser de estado sólido, la siguiente relación para las escalas de tiempo relevantes es generalmente válida
\[\tau_L \gg T_R \gg \tau_p. \nonumber \]
Conmutación Q activa
La Figura 4.5 muestra la dinámica principal de un láser de conmutación Q activa. El láser es bombeado por un pulso de bomba con una longitud del orden de la vida útil del estado superior, mientras que las pérdidas intracavitarias se mantienen lo suficientemente altas, para que el láser no pueda alcanzar el umbral. Por lo tanto, el medio láser actúa como un almacenamiento de energía. La energía solo se relaja mediante transiciones espontenosas y no radiativas. Entonces de repente se reduce la pérdida intracavitaria, por ejemplo por un espejo de cavidad giratoria. El láser se bombea muy por encima del umbral y el campo de luz se construye exponencialmente con la ganancia neta hasta que la energía del pulso se acerca a la energía de saturación del medio de ganancia. La ganancia se satura y se extrae, de manera que el láser es apagado por el propio pulso.
Un pulso típico de conmutación Q activa es asimétrico: El tiempo de subida es proporcional a la ganancia neta después de que el valor Q de la cavidad se conmute activamente a un valor alto. La intensidad lumínica crecimientos proporcionales a\(2g_0/T_R\). Cuando se agota la ganancia, el tiempo de caída depende principalmente del tiempo de decaimiento de la cavidad τp. Para pulsos cortos de conmutación Q es necesaria una longitud de cavidad corta, alta ganancia y un gran cambio en la cavidad Q. Si el interruptor Q no es rápido, el ancho de pulso puede estar limitado por la velocidad del interruptor. Los interruptores electroópticos y acústico-ópticos típicos son de 10 ns y 50 ns, respectivamente
Imagen eliminada debido a restricciones de derechos de autor. Consulte: Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 4.6: Pulso asimétrico de conmutación Q activa.
Por ejemplo, con un láser de\(\ce{Nd:YAG}\) microchip bombeado con diodos [6] que utiliza un interruptor electroóptico basado en pulsos de\(\ce{LiTaO3}\) conmutación Q tan cortos como 270 ps a tasas de repetición de 5 kHz, se han generado potencias pico de 25 kW a una potencia promedio de 34 mW y energía de pulso de 6.8\(\mu\) J (Figura 4.7).
Imagen eliminada debido a restricciones de derechos de autor. Por favor vea: Kafka, J. D., y T. Baer. “Láser de fibra dopado con erbio bloqueado en modo con modelado de pulso de solitón”. Letras Ópticas 14 (1989): 1269-1271.
Figura 4.7: Láser de microchip de conmutación Q usando un interruptor electroóptico. El pulso se mide con un alcance de muestreo [8]
Se obtuvieron resultados similares con Nd: YLF [7] y la configuración correspondiente se muestra en la Figura 4.8.
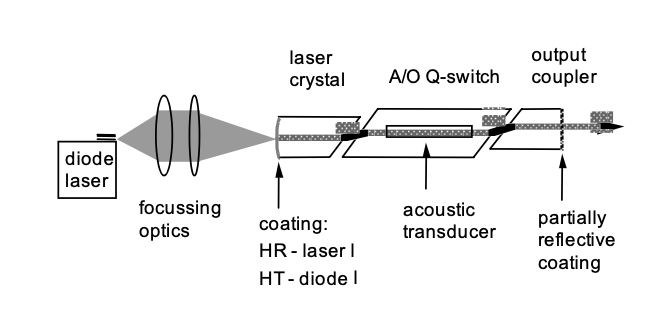
Pulsos Q-conmutados de frecuencia única
Los láseres de conmutación Q solo ofrecen una salida estable si oscilan en una sola frecuencia. Por lo general, esto no se logra automáticamente. Un método para lograrlo es sembrando con un láser de frecuencia única durante la operación de conmutación Q, de manera que ya haya una población en uno de los modos longitudinales antes de que se acumule el pulso. Este modo extraerá toda la energía antes de que los otros modos puedan hacer, ver Figura 4.9
Imagen eliminada debido a restricciones de derechos de autor. Consulte: Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 4.9: Intensidad de salida de un láser de conmutación Q sin a) y con siembra b).
Otra posibilidad para lograr una salida monomodo es usar un etalón en la cavidad o hacer que la cavidad sea tan corta, que solo un modo longitudinal esté dentro del ancho de banda de ganancia (Figura 4.10). Este suele ser solo el caso si la longitud de la cavidad es del orden de una vista milímetros o inferiores.El láser de microchip [6] [11] [10] se puede combinar con un modulador electro-óptico para lograr láseres de alta potencia de pico muy compactos con ancho de pulso de subnanosegundos (Figura 4.7).
Imagen eliminada debido a restricciones de derechos de autor. Consulte: Keller, U., Física láser ultrarrápida, Instituto de Electrónica Cuántica, Instituto Federal Suizo de Tecnología, ETH Hönggerberg—HPT, CH-8093 Zurich, Suiza.
Figura 4.10: En un láser de microchip el resonador puede ser tan corto, que solo hay un modo longitudinal dentro del ancho de banda de ganancia.
Teoría de la Conmutación Q Activa
Queremos obtener una idea de la acumulación de pulso y decaimiento del pulso de conmutación Q activa. Consideramos la situación ideal, donde la pérdida de la cavidad del láser puede cambiarse instantáneamente de un valor alto a un valor bajo, es decir, el factor de calidad se cambia de un valor bajo a un valor alto, respectivamente (Figura: 4.11)
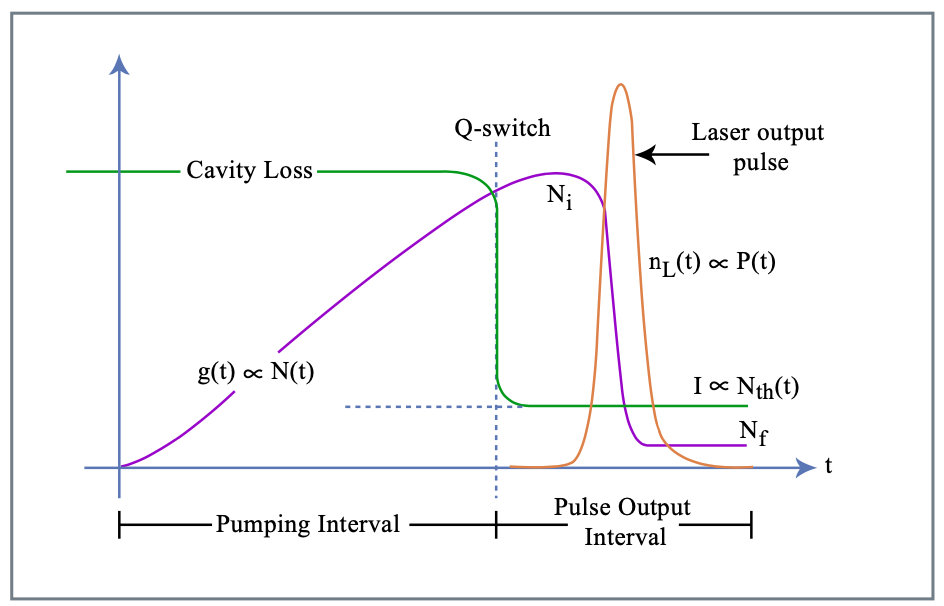
Intervalo de bombeo
Durante el bombeo con una velocidad de bombeo constante\(R_p\), proporcional a la pequeña ganancia de señal\(\text{g}_0\), se construye la inversión. Como no hay campo presente, la ganancia sigue la ecuación simple:
\[\dfrac{d}{dt} \text{g} = -\dfrac{\text{g} - \text{g}_0}{\tau_L}, \nonumber \]
o
\[\text{g}(t) = \text{g}_0 (1 - e^{-t/\tau_L}), \nonumber \]
Fase de acumulación de pulso:
Suponiendo una conmutación instantánea de las pérdidas de cavidad buscamos una solución aproximada a las ecuaciones de tasa a partir de la ganancia o inversión inicial\(\text{g}_i = hf_LN_{2i}/(2E_{sat}) = hf_LN_i/(2E_{sat})\), podemos dejar el índice de manera segura lejos ya que solo hay una población de estado superior. Además, asumimos que durante la acumulación del pulso la tasa de emisión estimulada es el término dominante que cambia la inversión. Luego, las ecuaciones de velocidad simplifican a\(\tau\)
\[\dfrac{d}{dt} \text{g} = -\dfrac{\text{g}P}{E_{sat_p}} \nonumber \]
\[\dfrac{d}{dt} P = \dfrac{2(\text{g} - l)}{T_R} P, \nonumber \]
lo que resulta en
\[\dfrac{dP}{d\text{g}} = \dfrac{2E_{sat}}{T_R} \left (\dfrac{l}{\text{g}} - 1\right ).\label{eq4.4.6} \]
Utilizamos las siguientes condiciones initales para el poder intracavitario\(P (t = 0) = 0\) y la ganancia inicial\(\text{g}(t = 0) = \text{g}_i = r \cdot l\). Tenga en cuenta,\(r\) significa cuántas veces se bombea el láser por encima del umbral después de que se opera el interruptor Q y las pérdidas intracavitarias se han reducido a\(l\). Entonces se\(\ref{eq4.4.6}\) puede resolver directamente y obtenemos
\[P(t) = \dfrac{2 E_{sat}}{T_R} \left (\text{g}_i - \text{g} (t) + l \ln \dfrac{\text{g} (t)}{\text{g}_i} \right ). \nonumber \]
De esta ecuación podemos deducir la potencia máxima del pulso, ya que el crecimiento de la potencia intracavitaria se detendrá cuando la ganancia se reduzca a las pérdidas,\(g(t) = l\), (Figura 4.11)
\[P_{\max} = \dfrac{2lE_{sat}}{T_R} (r - 1 - \ln r) \nonumber \]
\[= \dfrac{E_{sat}}{\tau_p} (r - 1 - \ln r).\label{eq4.4.9} \]
Esta es la primera cantidad importante del pulso generado y se muestra normalizada en la Figura 4.12.
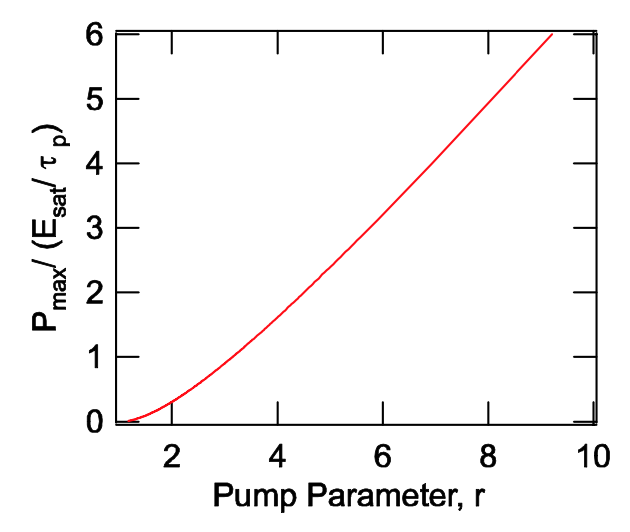
A continuación, podemos encontrar la ganancia final\(\text{g}_f\), que se alcanza una vez que se completa la emisión del pulso, es decir, es cuando el lado derecho de (4.38) desaparece
\[\left (\text{g}_i - \text{g}_f + l \ln \left ( \dfrac{\text{g}_f}{\text{g}_i} \right ) \right ) = 0 \nonumber \]
Usando el parámetro de bombeo\(r = \text{g}_i/l\), esto da como expresión para la relación entre la ganancia final e inicial o entre la inversión final e inicial
\[1 - \dfrac{\text{g}_f}{\text{g}_i} + \dfrac{1}{r} \ln \left (\dfrac{\text{g}_f}{\text{g}_i} \right ) = 0, \nonumber \]
\[1 - \dfrac{N_f}{N_i} + \dfrac{1}{r} \ln \left ( \dfrac{N_f}{N_i} \right ) = 0,\label{eq4.4.12} \]
que depende únicamente del parámetro de la bomba. Suponiendo además, que no hay pérdidas internas, entonces podemos estimar la energía de pulso generada por
\[E_P = (N_i - N_f) h f_L. \nonumber \]
Esto también es igual a la energía de impulso acoplada de salida ya que no se suponen pérdidas internas. Así, si la inversión final se hace pequeña, se puede extraer toda la energía almacenada en el medio de ganancia. Definimos la eficiencia de extracción de energía\(\eta\)
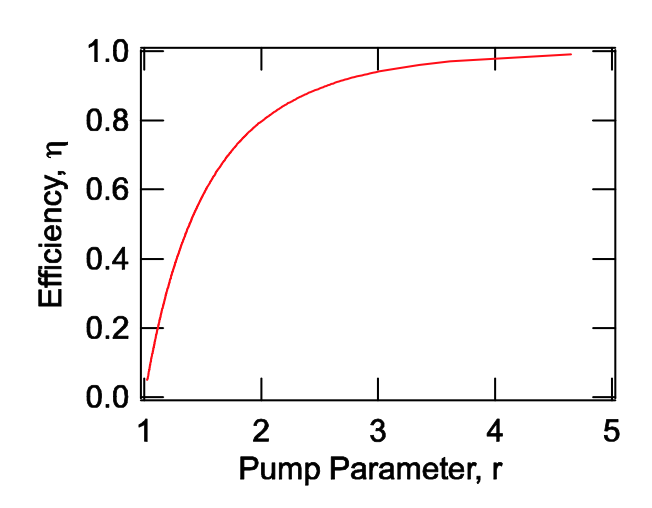
\[\eta = \dfrac{N_i - N_f}{N_i}, \nonumber \]
que nos dice cuánto de la energía inicialmente almacenada se puede extraer usando eq. (\(\ref{eq4.4.12}\))
\[\eta + \dfrac{1}{r} \ln (1 - \eta) = 0. \nonumber \]
Esta eficiencia se grafica en la Figura 4.13.
Tenga en cuenta que la eficiencia de extracción de energía solo depende del parámetro de la bomba\(r\). Ahora, la energía de pulso emitida se puede escribir como
\[E_P = \eta (r) N_i h f_L.\label{eq4.4.16} \]
y podemos estimar el ancho de pulso del pulso emitido por la relación entre la energía del pulso y la potencia máxima usando (\(\ref{eq4.4.9}\)) y (\(\ref{eq4.4.16}\))
\[\begin{array} {rcl} {\tau_{Pulse}} & = & {\dfrac{E_P}{2lP_{peak}} = \tau_p \dfrac{\eta (r)}{(r - 1 - \ln r)} \dfrac{N_i hf_L}{2lE_{sat}}} \\ {} & = & {\tau_p \dfrac{\eta (r)}{(r - 1 - \ln r)} \dfrac{\text{g}_i}{l}} \\ {} & \ & {\tau_p \dfrac{\eta (r) \cdot r}{(r - 1 - \ln r)}.} \end{array} \nonumber \]
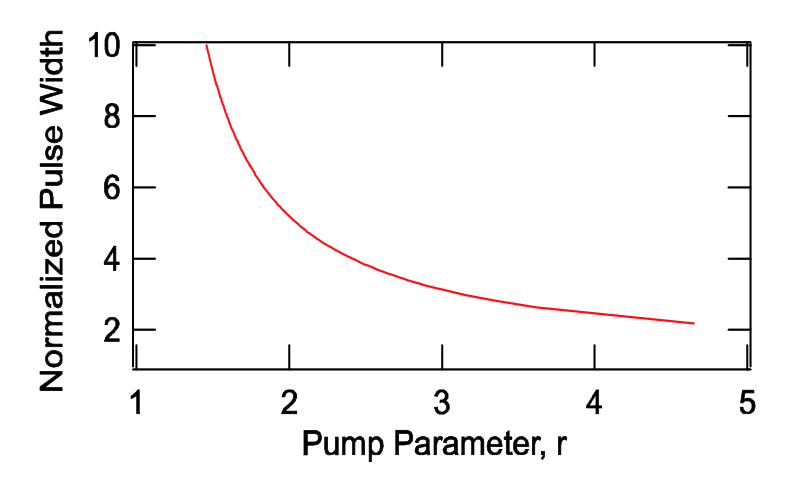
El ancho de pulso normalizado al tiempo de decaimiento de la cavidad\(\tau_p\) se muestra en la Figura 4.14.
Conmutación Q pasiva
En el caso de la conmutación Q pasiva la modulación de pérdida intracavitaria está per- formada por un absorbedor saturable, que introduce grandes pérdidas para bajas intensidades de luz y pequeñas pérdidas para alta intensidad.
Las oscilaciones de relajación se deben a un intercambio periódico de energía almacenada en el medio láser por la inversión y el campo de luz. Sin el absorbedor saturable estas oscilaciones se amortiguan. Si por alguna razón hay dos ganancias mucho en el sistema, el campo de luz puede acumularse rápidamente. Especialmente para una sección transversal de baja ganancia, la retroacción del campo láser en crecimiento en la inversión es débil y puede crecer aún más. Este crecimiento se ve favorecido ante la presencia de pérdida que satura con la intensidad de la luz. El láser se vuelve inestable, la intensidad de campo crece siempre y cuando la ganancia no se satura por debajo de la pérdida neta, ver Fig.4.15.
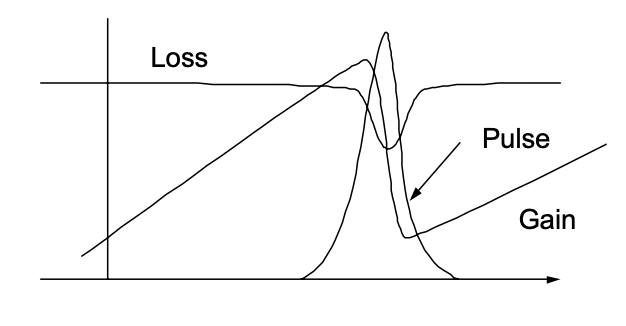
Ahora, queremos demostrar que el absorbedor saturable conduce a una desestabilización de las oscilaciones de relajación que resultan en el láser de pulso gigante.
Extendemos nuestro modelo láser mediante un absorbedor saturable como se muestra en la Figura 4.16
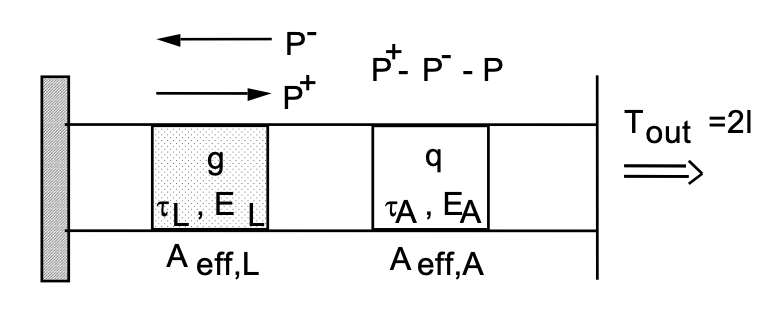
ecuaciones para un láser de conmutación Q pasiva
Hacemos los siguientes supuestos: Primero, los tiempos de relajación transversal de los modelos de dos niveles equivalentes para el medio de ganancia láser y para el absorbedor saturable son mucho más rápidos que cualquier otra dinámica en nuestro sistema, de manera que podemos usar ecuaciones de velocidad para describir la dinámica del láser. Segundo, asumimos que los cambios en la intensidad del láser, ganancia y absorción saturable son pequeños en una escala de tiempo del orden del tiempo de ida y vuelta\(T_R\) en la cavidad, (es decir, menos del 20%). Entonces, podemos usar las ecuaciones de tasa del láser como se derivó anteriormente más una ecuación correspondiente para la pérdida saturable q similar a la ecuación para la ganancia.
\[T_R \dfrac{dP}{dt} = 2(\text{g} - l - q) P\label{eq4.4.18} \]
\[T_R \dfrac{d \text{g}}{dt} = -\dfrac{\text{g} - \text{g}_0}{T_L} - \dfrac{\text{g} T_R P}{E_L} \nonumber \]
\[T_R \dfrac{dq}{dt} = -\dfrac{q -q_0}{T_A} - \dfrac{qT_R P}{E_A}\label{eq4.4.20} \]
donde\(P\) denota la potencia del láser,\(\text{g}\) la ganancia de amplitud por ida y vuelta,\(l\) las pérdidas de amplitud lineal por ida y vuelta,\(\text{g}_0\) la ganancia de señal pequeña por ida y vuelta y q0 las pérdidas insaturadas pero saturables por ida y vuelta. Las cantidades\(T_L = \tau_L/T_R\) y\(T_A = \tau_A/T_R\) son el tiempo de vida normalizado en estado superior del medio de ganancia y el tiempo de recuperación del absorbedor, normalizados al tiempo de ida y vuelta de la cavidad. Las energías\(E_L = h \nu A_{eff,L}/2^*\sigma_L\) y\(E_A = h \nu A_{eff,A}/2^*\sigma_A\) son las energías de saturación de la ganancia y del absorbedor, respectivamente.
Para láseres de estado sólido con tiempos de relajación de ganancia del orden de\(\tau_L \approx 100 \mu s\) o más, y tiempos de ida y vuelta de cavidad\(T_R \approx 10\) ns, obtenemos\(T_L \approx 10^4\). Además, asumimos absorbedores con tiempos de recuperación mucho más cortos que el tiempo de ida y vuelta de la cavidad, es decir\(\tau_A \approx 1 - 100\) ps, de manera que típicamente\(T_A ≈ 10^{-4}\) a\(10^{-2}\). Esto se puede lograr en semiconductores y puede diseñarse a voluntad mediante el crecimiento a baja temperatura del material semiconductor [20, 30]. Mientras el láser esté funcionando cw y modo único, el absorbedor seguirá la potencia instantánea del láser. Entonces, la absorción saturable se puede eliminar adiabáticamente, mediante el uso de la eq. (\(\ref{eq4.4.20}\))
\[q = \dfrac{q_0}{1 + P/P_A} \text{ with } P_A = \dfrac{E_A}{\tau_A}, \nonumber \]
y sustitución posterior en eq. (\(\ref{eq4.4.18}\)). Aquí,\(P_A\) está el poder de saturación del absorbedor. A una cierta cantidad de absorción saturable, las oscilaciones de relajación se vuelven inestables y se produce la conmutación Q. Para encontrar el criterio de estabilidad, linealizamos el sistema
\[T_R \dfrac{dR}{dt} = (\text{g} - l -q(P))P \nonumber \]
\[T_R \dfrac{d\text{g}}{dt} = -\dfrac{\text{g} - \text{g}_0}{T_L} - \dfrac{\text{g} T_R P}{E_L}. \nonumber \]
Solución estacionaria
Como en el caso del láser cw-running, el punto de operación estacionario del láser está determinado por el punto de ganancia neta cero
\[\begin{array} {rcl} {\text{g}_s} & = & {l + q_s} \\ {\dfrac{\text{g}_0}{1 + P_s/P_L}} & = & {l + \dfrac{q_0}{1 + P_s/P_A}.} \end{array}\label{eq4.4.24} \]
La solución gráfica de esta ecuación se muestra en la Figura 4.17
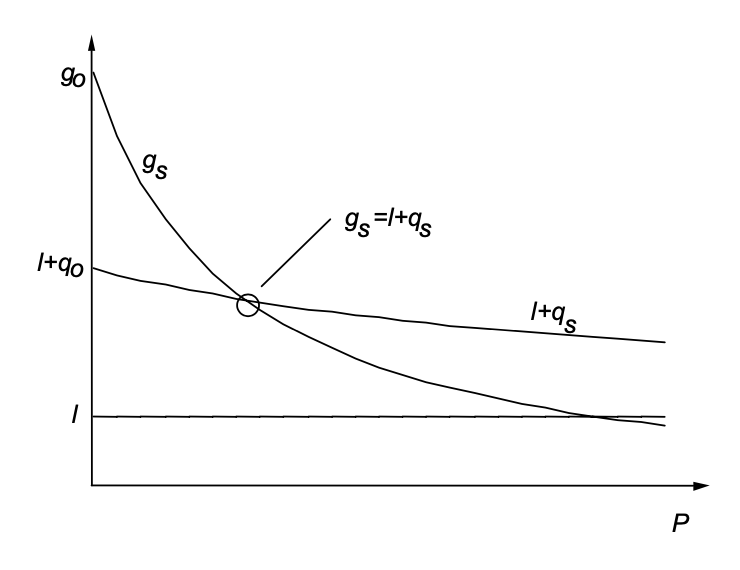
Estabilidad del punto de funcionamiento estacionario o la condición para la conmutación Q
Para el sistema linealizado, la matriz de coeficientes correspondiente a la Ec. (4.3.6) cambios solo por el absorbedor saturable [23]:
\[T_R \dfrac{d}{dt} \left (\begin{matrix} \Delta P_0 \\ Delta \text{g}_0 \end{matrix} \right ) = A \left (\begin{matrix} \Delta P_0 \\ Delta \text{g}_0 \end{matrix} \right ), \text{ with } A = \left (\begin{matrix} -2 \dfrac{dq}{dP}|_{cw} P_s & 2P_s \\ -\tfrac{gsT_R}{E_L} & -\tfrac{T_R}{\tau_{stim}} \end{matrix} \right )\label{eq4.4.25} \]
La matriz de coeficientes\(A\) sí tiene valores propios con parte real negativa, si y solo si su traza es negativa y el determinante es positivo lo que da como resultado dos condiciones
\[-2P \dfrac{dq}{dP}|_{cw} < \dfrac{r}{T_L} \text{ with } r = 1 + \dfrac{P_A}{P_L} \text{ and } P_L = \dfrac{E_L}{\tau_L},\label{eq4.4.26} \]
y
\[\dfrac{dq}{dP}|_{cw} \dfrac{r}{T_L} + 2 \text{g}_s \dfrac{r - 1}{T_L} > 0. \nonumber \]
Después de la cancelación de\(T_L\) terminamos con
\[\left |\dfrac{dq}{dP} \right |_{cw} < \left |\dfrac{d\text{g}_s}{dP} \right |_{cw}\label{eq4.4.28} \]
Para un láser que comienza a oscilar por sí solo, la relación\(\ref{eq4.4.28}\) se cumple automáticamente ya que la ganancia de señal pequeña es mayor que las pérdidas totales, ver Figura 4.17. La desigualdad (\(\ref{eq4.4.26}\)) tiene una explicación física simple. El lado derecho de (\(\ref{eq4.4.26}\)) es el tiempo de relajación de la ganancia hacia el equilibrio, a una potencia de bombeo dada y una potencia láser constante. El lado izquierdo es el tiempo de decaimiento de una fluctuación de potencia del láser a ganancia fija. Si la ganancia no puede reaccionar lo suficientemente rápido a las fluctuaciones de la potencia del láser, las oscilaciones de relajación crecen y dan como resultado una conmutación Q pasiva del láser.
Como se puede ver en la Ec. \(\ref{eq4.4.24}\)y la Eq. (\(\ref{eq4.4.26}\)), obtenemos
\[-2T_L P \dfrac{dq}{dP}|_{cw} = 2T_L q_0 \dfrac{\tfrac{P}{\chi P_L}}{(1 + \tfrac{P}{\chi P_L})^2}|_{cw} < r_s \text{ with } \chi = \dfrac{P_A}{P_L},\label{eq4.4.29} \]
donde\(\chi\) es una “rigidez” efectiva del absorbedor contra la saturación cw. La relación de estabilidad\(\ref{eq4.4.29}\) se visualiza en la Figura 4.18.
Imagen eliminada debido a restricciones de derechos de autor. Por favor vea: Kaertner, Franz, et al. “Control de la dinámica láser de estado sólido mediante dispositivos semiconductores”. Ingeniería Óptica 34, núm. 7 (julio de 1995): 2024-2036.
Figura 4.18: Representación gráfica de la relación de estabilidad de conmutación CW-Q para diferentes productos\(2q_0T_L\). La rigidez cw utilizada para las parcelas es\(\chi = 100\).
La tendencia de un láser a cambiar Q aumenta con el producto\(q_0T_L\) y disminuye si el absorbedor saturable es difícil de saturar, es decir\(\chi \gg 1\). Como se puede deducir de la Figura 4.18 y la eq. (\(\ref{eq4.4.26}\)), el láser nunca puede Q-switch, es decir, el lado izquierdo de la eq. (\(\ref{eq4.4.26}\)) es siempre menor que el lado derecho, si la cantidad
\[MDF = \dfrac{2q_0T_L}{\chi} < 1\label{eq4.4.27} \]
es menor que 1. La abreviatura MDF significa fuerza impulsora de bloqueo de modo, a pesar de que la expresión (\(\ref{eq4.4.27}\)) gobierna la inestabilidad del Q-switching. Veremos, en la siguiente sección, la conexión de este parámetro con bloqueo de modo. Para láseres de estado sólido con tiempos de vida de estado superior largos, cantidades ya muy pequeñas de absorción saturable, incluso una fracción de un porcentaje, pueden conducir a una fuerza impulsora de bloqueo de modo lo suficientemente grande como para impulsar el láser a la conmutación Q. La Figura 4.19 muestra las regiones en el plano\(\chi\) −\(P/P_L\) - donde la conmutación Q puede ocurrir para MDF fijo de acuerdo con la relación (\(\ref{eq4.4.26}\)). El área por encima del valor MDF correspondiente es la región de conmutación Q. Para MDF < 1, la conmutación CW-Q no puede ocurrir. Por lo tanto, si se tiene que diseñar un láser CW-Q conmutado, uno tiene que elegir un absorbedor con un MDF >1. Cuanto más se encuentre el punto de operación en el dominio de conmutación CW-Q, más pronunciada será la conmutación CW-Q. Para entender la naturaleza de la inestabilidad observamos la solución eigen y los valores propios de las ecuaciones linealizadas de movimiento\(\ref{eq4.4.25}\)
Imagen eliminada debido a restricciones de derechos de autor. Por favor vea: Kaertner, Franz, et al. “Control de la dinámica láser de estado sólido mediante dispositivos semiconductores”. Ingeniería Óptica 34, núm. 7 (julio de 1995): 2024-2036.
Figura 4.19: Para un valor dado del MDF, la conmutación CW-Q ocurre en el área por encima de la curva correspondiente. Para un valor MDF inferior a 1 CW-Qswitching no puede ocurrir.
\[\dfrac{d}{dt} \left (\begin{matrix} \Delta P_0 (t) \\ \Delta g_0 (t) \end{matrix} \right ) = s \left (\begin{matrix} \Delta P_0 (t) \\ \Delta g_0 (t) \end{matrix} \right ) \nonumber \]
lo que da como resultado los valores propios
\[sT_R = \dfrac{A_{11} + A_{22}}{2} \pm j \sqrt{A_{11}A_{22} - A_{12}A_{21} - \left ( \dfrac{A_{11} + A_{22}}{2} \right )^2}. \nonumber \]
Con los elementos de la matriz de acuerdo a la eq. (\(\ref{eq4.4.25}\)) obtenemos
\[s = \dfrac{-\tfrac{2}{T_R} \tfrac{dq}{dP}|_{cw} P_s - \tfrac{1}{\tau_{stim}}}{2} \pm j \omega_Q \nonumber \]
\[\omega_Q = \sqrt{-\dfrac{2}{T_R} \dfrac{dq}{dP}|_{cw} P_s \dfrac{r}{\tau_L} + \dfrac{r - 1}{\tau_p \tau_L} - \left (\dfrac{-\tfrac{2}{T_R} \tfrac{dq}{dP}|_{cw} P_s - \tfrac{1}{\tau_{stim}}}{2} \right )^2} \nonumber \]
donde el parámetro de la bomba ahora se define como la relación entre la ganancia de señal pequeña las pérdidas totales en estado estacionario, es decir\(r = g_0/(l + q_s)\). Esta expresión un tanto larga muestra claramente, que cuando el sistema se vuelve inestable\(-2\dfrac{dq}{dP} |_{cw} P_s > \dfrac{T_R}{\tau_{stim}}\),\(\tau_L \gg \tau_p\), con, hay una creciente oscilación con la frecuencia
\[\omega_Q \approx \dfrac{r - 1}{\tau_p \tau_L} \approx \dfrac{1}{\tau_p \tau_{stim}}. \nonumber \]
Es decir, la conmutación Q pasiva puede entenderse como una desestabilización de las oscilaciones de relajación del láser. Si el sistema está solo ligeramente en el régimen inestable, la frecuencia de la oscilación de conmutación Q es cercana a la frecuencia de oscilación de relajación. Si definimos la tasa de crecimiento\(\gamma_Q\), introducida por el absorbedor saturable como un prametro, los valores eigen pueden escribirse como
\[s = \dfrac{1}{2} \left ( \gamma_Q - \dfrac{1}{\tau_{stim}} \right ) \pm j \sqrt{\gamma_Q \dfrac{r}{\tau_L} + \dfrac{r - 1}{\tau_p \tau_L} - \left (\dfrac{\gamma_Q - \tfrac{1}{\tau_{stim}}{2} \right )^2}. \nonumber \]
La Figura 4.20 muestra la gráfica del locus radicular para un sistema con y sin un absorbedor sat- able. El absorbedor saturable desestabiliza las oscilaciones de relajación. El tipo de bifurcación se llama bifurcación Hopf y resulta en una oscilación.
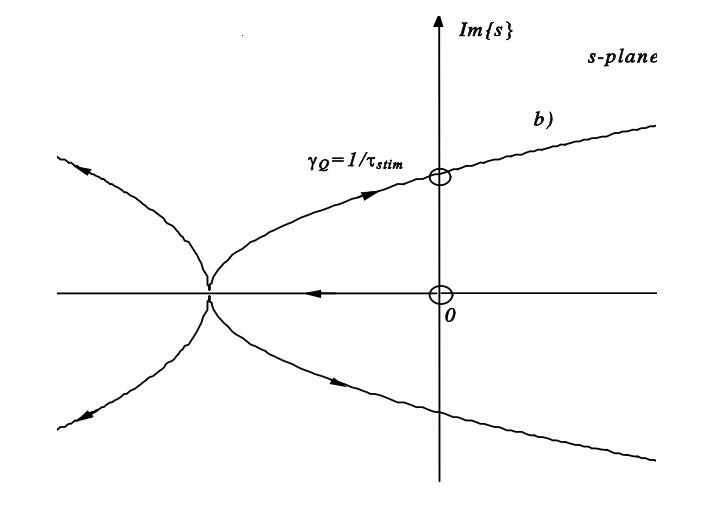
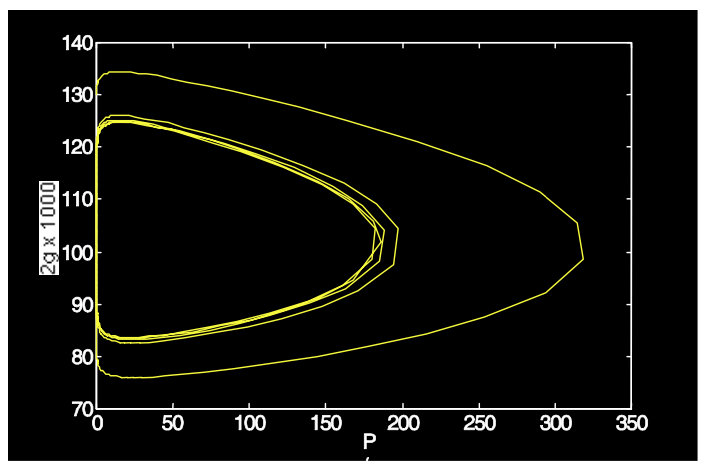
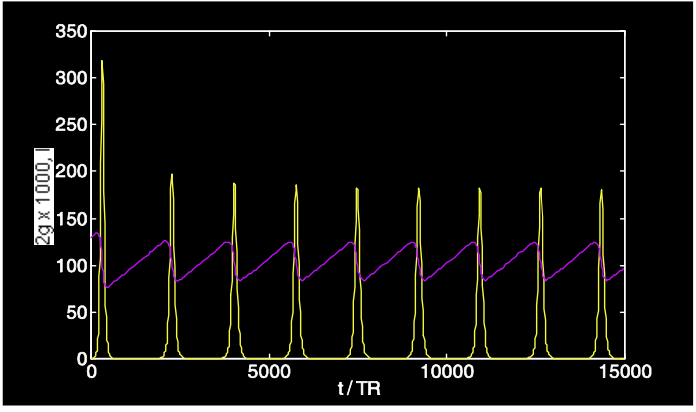
Como ejemplo, consideramos un láser con los siguientes parámetros:\(\tau_L = 250 \mu s\),,\(T_R = 4ns\),\(2l_0 = 0.1\),\(2q_0 = 0.005\),\(2g_0 = 2\),\(P_L/P_A = 100\). Las ecuaciones de tasa se resuelven numéricamente y se muestran en las Figuras 4.21 y 4.22.
