10.4: Interferometría Espectral y SPIDER
- Page ID
- 84988
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Interferometría de Fase Espectral para Reconstrucción Directa de Campo Eléctrico (SPI-DER) evita la reconstrucción iterativa del perfil de fase. Los algoritmos iterativos de transformada de Fourier tienen la desventaja de que a veces consumen bastante tiempo, impidiendo la caracterización de pulsos en tiempo real. Además, para las formas de pulso “patológicas”, la reconstrucción es difícil o incluso imposible. Matemáticamente no está probado que los algoritmos de recuperación sean poco ambiguos, especialmente en presencia de ruido.
La interferometría de cizallamiento espectral proporciona un método elegante para superar estas desventajas. Esta técnica ha sido introducida por primera vez por C. Iaconis y I.A. Walmsley en 1999 [11] y denominada interferometría de fase espectral para la reconstrucción directa de campo eléctrico - SPIDER. Antes de discutir SPIDER veamos la interferometría espectral en general
Interferometría espectral
El espectro de un pulso se puede medir fácilmente con un espectrómetro. El pulso sería completamente conocido, si pudiéramos determinar la fase a través del espectro. Para determinar esta interferometría espectral de fase desconocida para la medición de pulsos ha sido propuesta desde el principio por Froehly y otros [12]. Si tuviéramos un pulso bien referenciado con campo\(E_R(t)\), superpongamos el campo eléctrico desconocido\(E_S(t)\) retardado con el pulso de referencia e interferirlos en un espectrómetro, ver Figura 10.21, obtenemos para la salida del espectrómetro
\[E_I (t) = E_R (t) + E_s (t - \tau) \nonumber \]
\[\hat{S} (\omega) = \left | \int_{-\infty}^{+\infty} E_I (t) e^{-j \omega t} dt \right |^2 = \left | \hat{E}_R (\omega) + \hat{E}_S (\omega)^{-j \omega \tau} \right |^2 \nonumber \]
\[= \hat{S}_{DC} (\omega) + \hat{S}^{(-)} (\omega) e^{j \omega \tau} + \hat{S}^{(+)} (\omega) e^{-j \omega \tau} \nonumber \]
con
\[\hat{S}^{(+)} (\omega) = \hat{E}_R^* (\omega) \hat{E}_S (\omega) \nonumber \]
\[\hat{S}^{(-)} (\omega) = \hat{S}^{(+)*} (\omega) \nonumber \]
Donde (+) y (-) indican como antes, señales de “frecuencia” positivas y negativas bien separadas, donde la “frecuencia” ahora está relacionada\(\tau\) en lugar de\(\omega\).
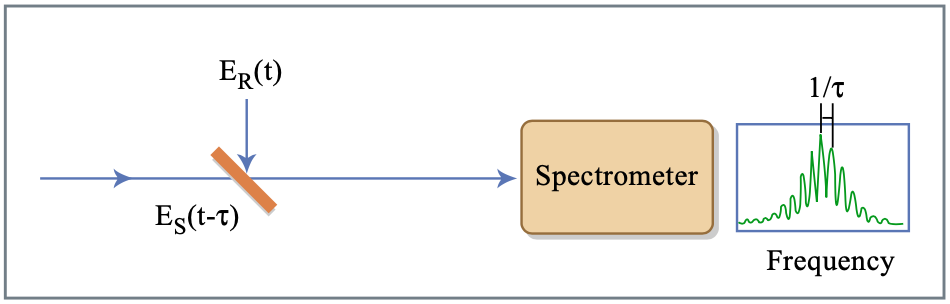
Figura por MIT OCW.
Si\(\tau\) se elige lo suficientemente grande, el espectro de transformada inversa de Fourier da como\(S(t) = F^{-1} \{ \hat{S} (\omega) \}\) resultado señales bien separadas, ver Figura 10.22.
\[S(t) = S_{DC} (t) + S^{(-)} (t + \tau) + \hat{S}^{(+)} (t - \tau) \nonumber \]
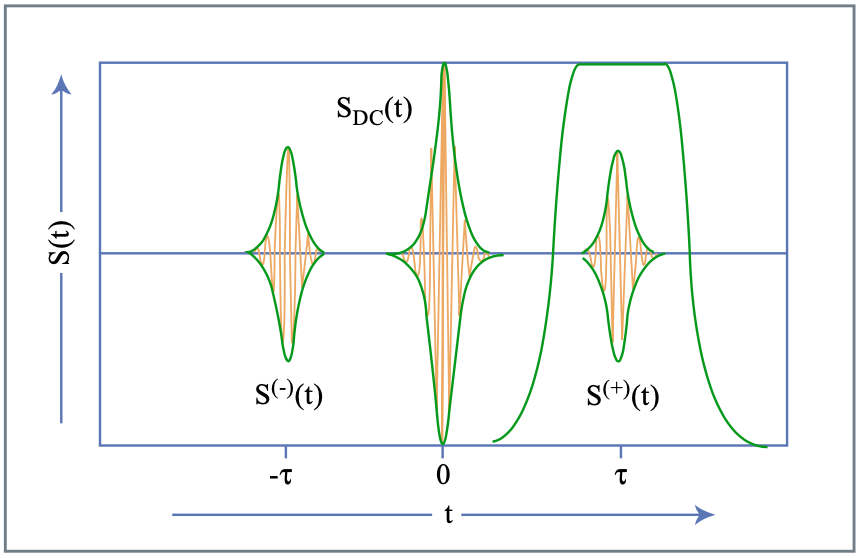
Figura por MIT OCW.
Podemos aislar el término de frecuencia positiva o negativa con un filtro en el dominio del tiempo. La transformación posterior del término correspondiente al dominio de frecuencia y el cálculo de la fase espectral de uno de los términos da como resultado la fase espectral de la señal hasta la fase conocida del pulso de referencia y una contribución de fase lineal desde el retardo.
\[\Phi^{(+)} (\omega) = \text{arg} \{ \hat{S}^{(+)} (\omega) e^{j \omega \tau} \} = \varphi_S (\omega) -\varphi_R (\omega) + \omega \tau \nonumber \]
ARAÑA
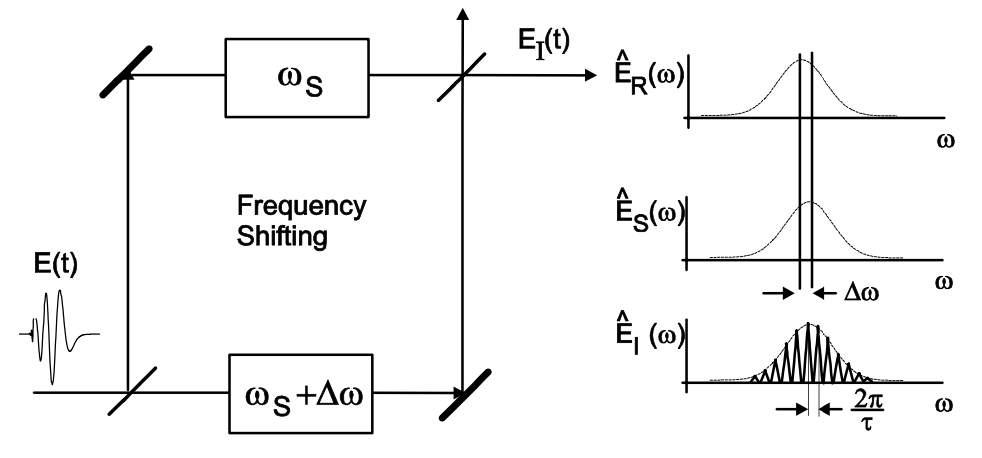
¿Qué podemos hacer si no tenemos un pulso de referencia bien caracterizado? C. Iaconis y I.A. Walmsley [?] se le ocurrió la idea de generar dos espectros convertidos hacia arriba ligeramente desplazados en frecuencia e investigar la interferencia espectral de estas dos copias, ver Figura 10.23. Utilizamos
\[E_R (t) = E(t) e^{j \omega_S t} \nonumber \]
\[E_S (t) = E(t - \tau) e^{j(\omega_S + \Omega) t} \nonumber \]
\[E_I (t) = E_R (t) + E_S (t) \nonumber \]
donde\(\omega_s\) y\(\omega_s + \Omega\) son las dos frecuencias utilizadas para la conversión ascendente y\(\Omega\) se llama el cizallamiento espectral entre los dos pulsos. \(E(t)\)es el campo eléctrico desconocido con espectro
\[\hat{E} (\omega) = \left |\hat{E} (\omega) \right | e^{j \varphi (\omega)} \nonumber \]
La interferometría espectral que utiliza estos pulsos de señal y referencia especialmente construidos da como resultado
\[\hat{S} (\omega) = \left | \int_{-\infty}^{+\infty} E_I (t) e^{-j \omega t} dt \right |^2 = \hat{S}_{DC} (\omega) + \hat{S}^{(-)} (\omega) e^{j \omega \tau} + \hat{S}^{(+)} e^{-j \omega \tau} \nonumber \]
\[\hat{S}^{(+)} (\omega) = \hat{E}_R^* (\omega) \hat{E}_S (\omega) = \hat{E}^* (\omega - \omega_s) \hat{E} (\omega - \omega_s - \Omega) \nonumber \]
\[\hat{S}^{(-)} (\omega) = \hat{S}^{(+)*} (\omega)\label{eq10.4.14} \]
La fase\(\psi (\omega) = \text{arg} [\hat{S}^{(+)} e^{-j \omega \tau}]\) derivada del componente espectral positivo aislado es
\[\psi (\omega) = \varphi (\omega - \omega_s - \Omega) - \varphi (\omega - \omega_s) - \omega \tau.\label{eq10.4.15} \]
La fase lineal se\(\omega \tau\) puede sustraer después de la determinación independiente del retardo de tiempo\(\tau\). Es obvio que el cizallamiento espectral\(\Omega\) tiene que ser pequeño comparado con el ancho de banda espectral\(\Delta \omega\) del pulso, ver Figura 10.23. Luego la diferencia de fase en la Ec. (\(\ref{eq10.4.13}\)) es proporcional al retardo de grupo en el pulso, i.e.
\[-\Omega \dfrac{d\varphi}{d \omega} = \psi (\omega), \nonumber \]
o
\[\varphi (\omega) = -\dfrac{1}{\Omega} \int_{0}^{\omega} \psi (\omega') d\omega'. \nonumber \]
Tenga en cuenta que un error\(\Delta \tau\) en la calibración del retardo de tiempo\(\tau\) da como resultado un error en el chirp del pulso
\[\Delta \varphi (\omega) = -\dfrac{\omega^2}{2 \Omega} \Delta \tau.\label{eq10.4.18} \]
Por lo tanto, es importante elegir un cizallamiento espectral\(\Omega\) que no sea demasiado pequeño. ¿Qué tan pequeño tiene que ser? Esencialmente se muestrear la fase con un espaciado muestral\(\Omega\). El teorema de Nyquist establece que podemos resolver de manera única un pulso en el dominio del tiempo si solo es distinto de cero sobre una longitud\([-T, T]\), donde\(T = \tau /\Omega\). Por otro lado la cizalla\(\Omega\) tiene que ser lo suficientemente grande para que las franjas en el espectro puedan resolverse con el espectrómetro disponible.
Configuración de SPIDER
Seguimos el trabajo de Gallmann et al. [?] que se puede utilizar para la caracterización de pulsos solo unos pocos ciclos ópticos de duración. La configuración se muestra en la Figura 10.24.
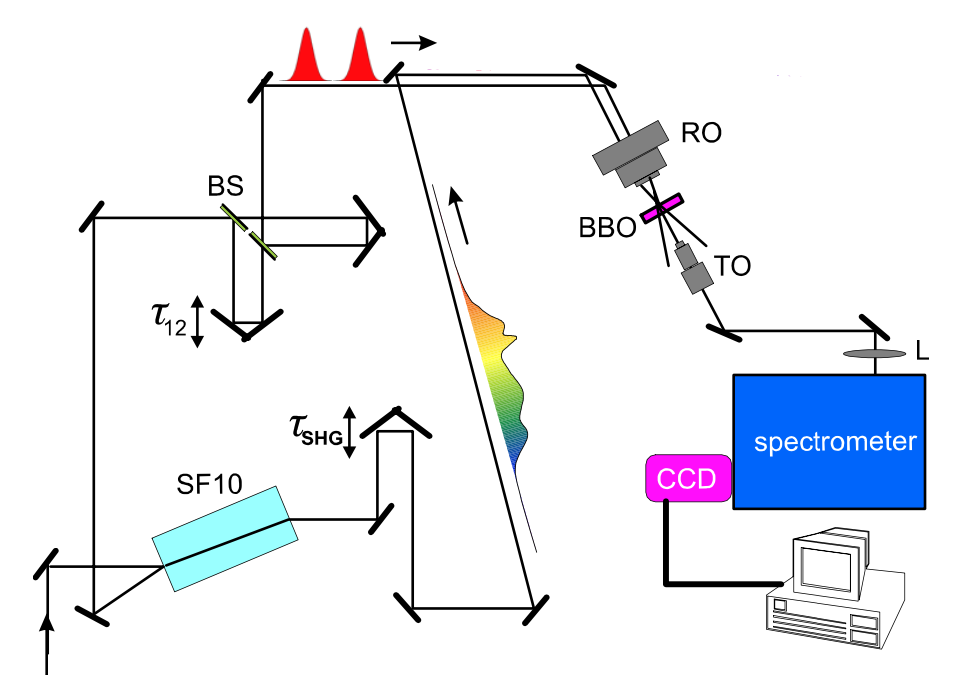
Cortesía de Richard Ell. Usado con permiso.
Generación de dos réplicas sin chirp adicional:
Un interferómetro tipo Michelson genera dos réplicas sin chirrido. Los divisores de haz BS tienen que ser de banda ancha, no para distorsionar los pulsos. El retardo\(\tau\) entre las dos réplicas tiene que ser elegido correctamente, es decir, en la configuración mostrada fue de aproximadamente 400-500 fs correspondientes a 120-150\(\mu\) m de distancia en el espacio.
Cizalla espectral:
Las copias espectralmente cizalladas del pulso son generadas por generación de suma-frecuencia (SFG) con haces cuasi-monocromáticos a frecuencias\(\omega_s\) y\(\omega_s + \Omega\). Estas señales cuasimonocromáticas son generadas por un fuerte chirp- ing de una tercera réplica (ver Figura 10.24) del pulso de señal que se propaga a través de una losa de vidrio fuertemente dispersiva. Para la configuración actual estimamos para el ensanchamiento de un pulso gaussiano debido a la dispersión vítrea de 5 fs a aproximadamente 6ps. Tal estiramiento de más de un factor de mil asegura que SFG ocurre dentro de un ancho de banda óptico menor a 1 nm, una señal cuasi-monocromática. El ajuste de la superposición temporal\(\tau_{SHG}\) con las dos réplicas no chirpeadas es posible mediante una segunda línea de retardo. El pulso rayado se puede calcular por propagación del pulso de señal\(E(t)\) a través del medio fuertemente dispersivo con característica de transferencia
\[H_{glass} (omega) = e^{-j D_{glass} (\omega -\omega_c)^2/2} \nonumber \]
descuidar el retardo de grupo lineal y términos de dispersión de orden superior. Se aferró a la parte analítica del campo eléctrico del pulso rayado que sale del bloque de vidrio por convolución con la característica de transferencia
\[E_{stretch} (t) = \int_{-\infty}^{+\infty} \hat{E} (\omega) e^{-j D_{glass} (\omega - \omega_c)^2/2} e^{j \omega t} d\omega = \nonumber \]
\[= e^{jt^2/(2 D_{glass}) e^{j \omega_c t} \int_{-\infty}^{+\infty} \hat{E} (\omega) e^{-jD_{glass} ((\omega - \omega_c) - t/D_{glass}^2)/2} d \omega \nonumber \]
Si el espectro del pulso es lo suficientemente suave, se puede aplicar el método de fase estacionaria para la evaluación de la integral y obtenemos
\[E_{stretch} (t) \propto e^{j \omega_c (t + t^2/(2D_{glass})} \hat{E} (\omega = \omega_c + t/D_{glass}) \nonumber \]
Por lo tanto, la intensidad de campo en la posición donde la frecuencia instantánea es
\[\omega_{inst} = \dfrac{d}{dt} \omega_c (t + t^2/(2D_{glass})) = \omega_c + t/D_{glass}\label{eq10.4.23} \]
viene dada por la amplitud espectral a esa frecuencia,\(\hat{E} (\omega = \omega_c + t/D_{glass})\). Para grandes estiramientos, i.e.
\[|\tau_p/D_{glass}| \ll |\Omega|\label{eq10.4.24} \]
se puede suponer que la conversión ascendente es cuasi monocromática.
SFG:
Un cristal BBO (acuñado 10-50\(\mu\) m) se utiliza para SFG tipo I de fase emparejada. La adaptación de fase de tipo II permitiría mayores anchos de banda de aceptación. Los pulsos son enfocados en el cristal BBO mediante un objetivo reflectante compuesto por espejos curvos. La señal es colimada por otro objetivo. Debido al SFG con el pulso chirped el cizallamiento espectral se relaciona con el retardo entre ambos pulsos\(\tau\), determinado por la Ec. (\(\ref{eq10.4.23}\)) ser
\[\Omega = -\tau/ D_{glass}.\label{eq10.4.25} \]
Tenga en cuenta que las condiciones (\(\ref{eq10.4.24}\)) y (\(\ref{eq10.4.25}\)) son consistentes con el hecho de que el retardo entre los dos pulsos debe ser mucho mayor que el ancho de pulso,\(\tau_p\) lo que también permite la separación de los espectros en la Fig. 10.22 para determinar la fase espectral usando el método de transformada de Fourier. Para la caracterización de pulsos sub-10fs un espesor de cristal alrededor de 30μm es un buen compromiso. La eficiencia sigue siendo lo suficientemente alta para las cámaras CCD refrigeradas comunes, la dispersión ya es suficientemente baja y el ancho de banda de adaptación de fase lo suficientemente grande.
Detección de señal y reconstrucción de fase:
Una lente adicional enfoca la señal SPIDER en un espectrómetro con una cámara CCD en el plano de salida. El registro y análisis de datos se realiza con una computadora. La búsqueda inicial de una señal SPIDER se realiza mediante corte y detección Lock-In. La rueda troceadora se coloca de manera que los pulsos no chirped son modulados por la parte externa de la rueda y el pulso chirped por la parte interna de la rueda. La parte externa e interna tienen frecuencias de hendidura difentes. Una señal SPIDER es modulada por la frecuencia de diferencia (y suma) que es discriminada por el amplificador Lock-In. Una vez que se mide una señal, se puede obtener una mayor optimización mejorando la superposición espacial y temporal de los haces en el cristal BBO.
Una de las ventajas de SPIDER es que solo se extrae de los datos medidos la información de fase faltante. Debido al ancho de banda limitado de adaptación de fase del cristal no lineal y la respuesta espectral de la rejilla y CCD, el espectro fundamental no se imagina en su forma original sino con intensidad reducida en las alas espectrales. Pero mientras las franjas de interferencia sean visibles, cualquier amortiguación en las alas espectrales y la deformación del espectro no impacte en el proceso de reconstrucción de fase, la técnica SPIDER entrega la información correcta. Luego se genera la traza SPIDER detectando la interferencia espectral de los pulsos
\[E_R (t) = E(t) \hat{E} (\omega_s) e^{j \omega_S t} \nonumber \]
\[E_S (t) = E(t - \tau) \hat{E} (\omega_s + \Omega) e^{j (\omega_S + \Omega) t \nonumber \]
\[E_I (t) = E_R (t) + E_S (t) \nonumber \]
Los componentes de frecuencia positiva y negativa de la traza SIDER son entonces de acuerdo con las Eqs. (\(\ref{eq10.4.14}\))
\[\hat{S}^{(+)} (\omega) = \hat{E}_R^* (\omega) \hat{E}_S (\omega) = \hat{E}^* (\omega - \omega_s - \Omega) \hat{E}^* (\omega_s) \hat{E} (\omega_s - \Omega) \nonumber \]
\[\hat{S}^{(-)} (\omega) = \hat{S}^{(+)*} (\omega) \nonumber \]
y la fase\(\psi (\omega) = \text{arg} [\hat{S}^{(+)} (\omega) e^{-j \omega \tau}]\) derivada de la sustracción de componente espectral positiva aislada ya la fase lineal es
\[\psi (\omega) = \varphi (\omega - \omega_s - \Omega) - \varphi (\omega - \oemga_s) - \varphi (\omega - \omega_s - \Omega) + \varphi (\omega_s - \Omega) - \varphi (\omega_s). \nonumber \]
Así, hasta una constante adicional entrega el retardo de grupo dentro del pulso a caracterizar. Un retraso grupal constante no tiene importancia física.
Calibración de arañas
Esta es la parte más crítica de la medición SPIDER. Hay tres cantidades a determinar con alta precisión y reproducibilidad:
- retraso\(\tau\)
- turno\(\omega_s\)
- cizalla\(\Omega\)
Retraso\(\tau\):
El retardo\(\tau\) es el desplazamiento temporal entre los pulsos no chirpeados. Aparece como un término de fase dependiente de la frecuencia en la fase SPIDER, Eqs. (\(\ref{eq10.4.15}\)) y conduce a un error en el chirp del pulso si no se sustrae correctamente, vea la Ec. (\(\ref{eq10.4.18}\)).
Una determinación de\(\tau\) debe hacerse preferentemente con los pulsos detectados por el espectrómetro pero sin el cizallamiento espectral para que las franjas observadas estén todas espaciadas exactamente por\(1/\tau\). Tal interferograma puede obtenerse bloqueando el pulso chirped y solapando las señales SHG individuales de los dos pulsos no chirpeados. Una transformada de Fourier del interferograma entrega el retardo deseado\(\tau\). En la práctica, esta técnica puede ser difícil de usar. Experimento y simulación muestran que los cambios ya menores de\(\tau\) (\(\pm 1\)fs) alteran significativamente la duración del pulso reconstruido (\(\approx \pm\)1 - 10%).
Otra forma de determinación de\(\tau\) es la siguiente. Como ya se mencionó,\(\tau\) es accesible por una diferenciación de la fase SPIDER con respecto a\(\omega\). \(\tau\)Por lo tanto, el retraso representa un GDD constante. Una determinación incorrecta de\(\tau\) es, por lo tanto, equivalente a una medición falsa de GDD. El GDD físico real del pulso se puede minimizar mediante una medición simultánea de IAC. El nivel máximo de señal, respectivamente, la traza más corta de IAC significa un GDD promedio de cero. La duración del pulso es entonces sólo limitada por dispersión de orden superior no dependiendo de\(\tau\). Después de la medición de IAC,\(\tau\) se elige el retardo de manera que la medición SPIDER proporcione la duración de pulso más corta. Esto se justifica porque a través del IAC sabemos que la duración del pulso sólo está limitada por dispersión de orden superior y no por el GDD\(\propto \tau\). La desventaja de este método es que se necesita una configuración adicional de IAC.
Desplazamiento\(\omega_s\):
El proceso SFG desplaza el espectro original por una frecuencia\(\omega_s \approx 300\) THz hacia frecuencias más altas equivalentes a aproximadamente 450nm cuando se caracterizan los pulsos Ti:zafiro. Si la configuración de SPIDER está bien ajustada, el cuadrado del interferograma SPIDER medido por el CCD es similar al espectro fundamental. Una determinación del desplazamiento se puede hacer correlacionando ambos espectros entre sí. La determinación de\(\omega_s\) solo influye también en la frecuencia a la que asignamos un valor de fase dado, que no es tan crítico.
Cizalla\(\Omega\):
El cizallamiento espectral es acrítico y puede ser estimado por la dispersión vítrea y el retraso\(\tau\).
Caracterización de Pulsos Láser Ti:Zafiro Sub-Dos
La configuración y el registro y procesamiento de datos se pueden optimizar de tal manera que el interferograma SPIDER y la fase reconstruida, GDD y envolvente de intensidad se visualizan en una pantalla con velocidades de actualización en el rango de 0.5-1s.
Las mediciones de SPIDER en tiempo real permitieron optimizar la compensación de dispersión externa que conduce a pulsos de 4.8 fs directamente desde un láser [13], ver Figura 10.25.
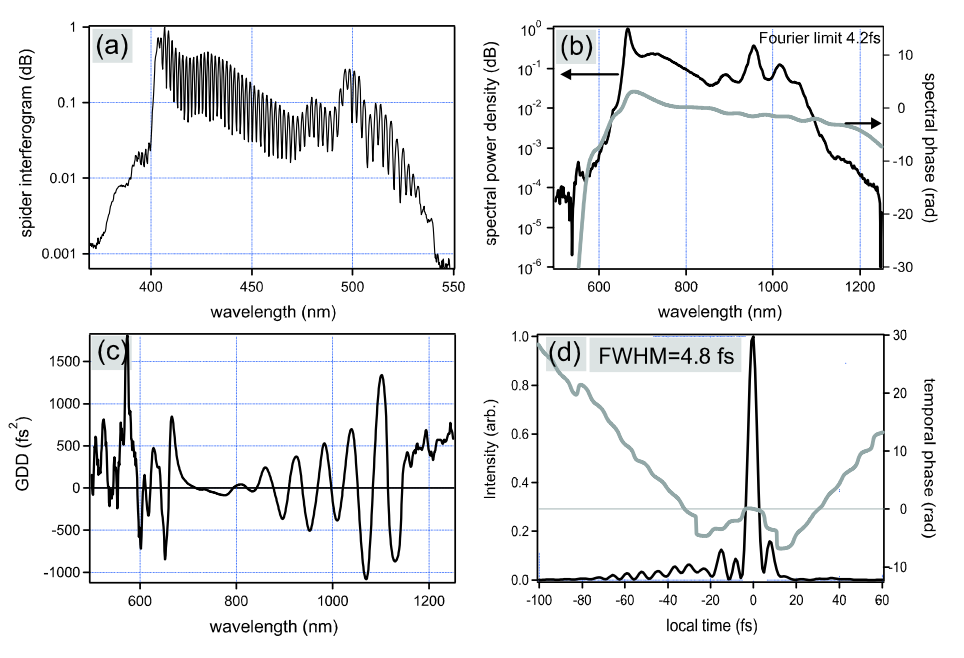
Cortesía de Richard Ell. Usado con permiso.
La Figura 10.25 (a) muestra el interferograma SPIDER detectado por la cámara CCD. El interferograma se modula hasta en 90%, el límite de resoluciones en el gráfico mostrado no puede resolver esto. La gran cantidad de franjas de interferencia asegura un cálculo de fase confiable. La Figura (b) muestra el espectro láser registrado por el analizador de espectro óptico en una escala logarítmica. La curva de fase espectral calculada se suma en esta gráfica. La pequeña pendiente de la curva de fase corresponde a un GD constante que es un cambio de tiempo sin importancia. La Figura 10.25 (c) representa el GDD obtenido de la fase por dos derivadas con respecto a la frecuencia angular\(\omega\). La última Figura (d) muestra la envolvente de intensidad con una duración de pulso FWHM de 4.8 fs junto con la curva de fase temporal.
Pros y contras de SPIDER
| Ventajas | Desventajas |
| extracción de fase analítica directa | configuración experimental compleja |
| sin espejos móviles u otros componentes | calibración precisa de retardo necesaria |
| posible caracterización en tiempo real | Espectro “compacto” necesario (sin intervalos de intensidad cero) |
| adquisición simple de datos 1-D | necesidad de una cámara CCD gastada |
| dependencia menor de la respuesta espectral del cristal no lineal y el espectrómetro |
Bibliografía
[1] K. Naganuma, K. Mogi, H. Yamada, “Método general para la medición de chirp de pulso de luz ultracorta”, IEEE J. de Quant. Elec. 25, 1225 - 1233 (1989).
[2] J. C. Diels, J. J. Fontaine, y F. Simoni, “Medición sensible a la fase de pulsos láser de femtosegundos de una cavidad de anillo”, en Actas de la Conf. Internacional sobre Láseres. 1983, STS Prensa: McLean, VA, p. 348-355. J. C. Diels et al. , "Control y medición de Formas Ultrashortas de Pulso (en Amplitud y Fase) con Precisión de Femtosegundos”, Óptica Aplicada 24, 1270-82 (1985).
[3] J.W. Nicholson, J.Jasapara, W. Rudolph, F.G. Ometto y A.J. Taylor, “Caracterización de campo completo de pulsos de femtosegundos por espectro y mediciones de correlación cruzada, “Opt. Let. 24, 1774 (1999).
[4] D. T. Reid, et al., Opt. Let. 22, 233-235 (1997).
[5] R. Trebino, “Compuerta óptica de frecuencia resuelta: la medición de
Pulsos láser ultracortos, "Kluwer Academic Press, Boston, (2000).
[6] Trebino, et al., Rev. Sci. Instr., 68, 3277 (1997).
[7] Kane y Trebino, Opt. Let., 18, 823 (1993).
[8] Stark, Recuperación de Imagen, Prensa Académica, 1987.
[9] L. Cohen, “Distribuciones de tiempo-frecuencia-una revisión," Actas del IEEE, 77, 941 - 981 (1989).
[10] L. Gallmann, D. H. Sutter, N. Matuschek, G. Steinmeyer y U. Keller, “Caracterización de pulsos ópticos sub-6fs con interferometría de fase espectral para reconstrucción directa de campo eléctrico”, Opt. Let. 24, 1314 (1999).
[11] C. Iaconis e I. A. Walmsley, Interferometría Espectral Auto-Referenciante para Medición de Pulsos Ópticos Ultracortos, IEEE J. de Quant. Elec. 35, 501 (1999).
[12] C. Froehly, A. Lacourt, J. C. Vienot, “Nociones de respuesta impulsionelle et de fonction de tranfert temporelles des pupilles opticques, justificaciones experimentales et aplicaciones”, Nouv. Rev. Optique 4, 18 (1973).
[13] Richard Ell, “Sub-Two Cycle Ti:Sapphire Laser and Phase Sensitive Nonlinear Optics”, PhD-thesis, Universidad de Karlsruhe (TH), (2003).

