9.3: Conexiones trifásicas

Es posible configurar sistemas usando fuentes conectadas delta o Y con cargas conectadas delta o Y. Un elemento a tener en cuenta es que los sistemas conectados delta son siempre sistemas de tres hilos, mientras que los sistemas conectados en Y pueden hacer uso de un cuarto cable neutro (el punto común al que se conectan las tres fuentes).

Sistemas Homogéneos

Los sistemas más sencillos son delta a delta y A-Y. Nos referiremos a estos como sistemas homogéneos ya que las estructuras del generador y la carga son similares. Los ejemplos se muestran en las Figuras\(\PageIndex{1}\) y\(\PageIndex{2}\), respectivamente.

Figura\(\PageIndex{1}\): Un generador conectado delta con una carga conectada delta (delta-delta).

Figura\(\PageIndex{2}\): Un generador conectado en Y con una carga conectada en Y (Y-Y). Se muestra el cuarto cable neutro opcional de centro a centro.

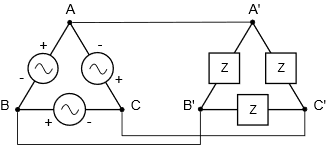
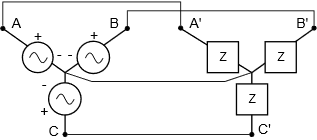
En estas configuraciones, cada tramo de la carga coincide con un tramo correspondiente del generador. En la configuración delta-delta de la Figura\(\PageIndex{1}\), debe ser obvio solo por inspección que el voltaje a través de cualquier tramo de carga debe ser igual al voltaje de la pata del generador correspondiente. Por ejemplo, la impedancia de carga conectada entre\(A'\) y\(B'\) debe ver el voltaje presentado por el generador situado entre\(A\) y\(B\) porque\(A\) está conectado directamente a\(A'\) como es\(B\) a\(B'\). De manera similar, para la configuración Y-Y de la Figura\(\PageIndex{2}\), la corriente a través de cualquier tramo de carga debe ser igual a la corriente que fluye a través de la pata asociada del generador ya que no hay otras trayectorias para la corriente entre\(A\)\(B\) y\(A'\), y\(B'\), y\(C\) y\(C'\).

Como la carga se equilibra y las patas del generador son idénticas excepto por su fase, debe darse el caso de que las tensiones y corrientes (y de ahí las potencias) para cada tramo de la carga deban ser las mismas, con excepción de la fase. Esto es cierto tanto para la configuración Y-Y como para la configuración delta-delta. El bit complicado aquí es la diferencia entre una corriente o voltaje de fuente (o carga) y la corriente o voltaje de línea.

\[\text{Line voltage is the voltage magnitude between any two conductors connecting the source to the load, excluding ground or common.} \nonumber \]

\[\text{Line current is the current magnitude flowing in any conductor connecting the source to the load, excluding ground or common.} \nonumber \]

Considera el sistema delta-delta de la Figura\(\PageIndex{1}\). Ya hemos establecido que el voltaje desarrollado por el generador\(A,B\) debe ser el mismo que el voltaje a través de la carga\(A',B'\). Por lo tanto, el voltaje medido desde el conductor A, A' al conductor B, B' debe ser el mismo que los voltajes de fuente y carga. En otras palabras, en la configuración delta-delta, los voltajes de fuente, carga y línea son todos iguales.

También encontramos que las corrientes de fuente y carga deben ser las mismas para la configuración delta-delta, sin embargo, esto no implica que la corriente que fluye a través del cable que se conecta\(A\) a\(A'\) deba ser la misma que la corriente que fluye a través del generador o la carga. Después de todo, dos cables de carga se conectan a\(A'\), no solo a uno. Por definición, la corriente que fluye a través de ese cable es la corriente de línea y, por lo tanto, en una configuración delta-delta, la corriente de línea no es la misma que la corriente de fuente o de carga. Para evitar confusiones, la tensión o corriente asociada con una sola pata se conoce como la tensión o corriente de fase versus la tensión o corriente de línea.

Volviendo a la configuración Y-Y de la Figura\(\PageIndex{2}\), vemos una situación opuesta. La fuente, la carga y las corrientes de línea serán todas iguales. Por otro lado, la tensión de línea comprende dos generadores, no uno (por ejemplo, de\(A\) a\(B\) o de\(B\) a\(C\)). Así, para una configuración Y-Y los voltajes de fuente y carga son los mismos, pero no son iguales a la tensión de línea (ni es dos veces, gracias al desplazamiento de fase).

Determinación del voltaje y la corriente de la línea

Para determinar el voltaje de línea para un generador conectado en Y (y de manera similar, la corriente de línea para un generador conectado delta), es útil examinar una gráfica fasora de las tensiones individuales del generador. Esto se muestra en la Figura\(\PageIndex{3}\). Tenemos tres voltajes de idéntica amplitud, siendo la única diferencia entre ellos su fase. Cada vector está separado de los demás por 120 grados. Además, cada generador individual está conectado desde el punto común a uno de los puntos externos de\(A\),\(B\) y\(C\). El voltaje de línea se define como el potencial existente entre dos cualesquiera si estos tres puntos. Si bien es posible simplemente restar un voltaje de generador de otro para llegar a la diferencia, existe una buena solución gráfica de la cual podemos derivar una fórmula precisa para el voltaje de línea dado el voltaje del generador.

Figura\(\PageIndex{3}\): Diagrama fasor del generador conectado en Y

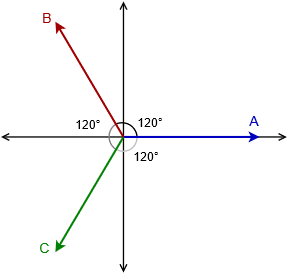
Comenzamos por enfocarnos en los cuadrantes dos y tres de la trama fasorial. Esta sección se vuelve a dibujar en la Figura\(\PageIndex{4}\). En realidad, se pueden utilizar dos vectores cualesquiera para la siguiente prueba, pero este par resulta ser particularmente conveniente en su orientación.

Figura\(\PageIndex{4}\): Resolviendo el voltaje de línea de un generador conectado en Y.

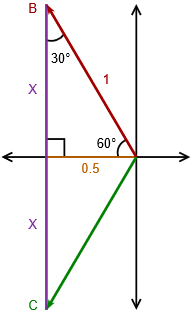
Para facilidad de uso normalizaremos la magnitud del voltaje del generador a la unidad. Lo que vemos es que los\(C\) vectores\(B\) y están divididos perfectamente por el eje horizontal; lo que está por encima del eje se refleja perfectamente debajo de él. En la porción superior encontramos un triángulo rectángulo con una hipotenusa de unidad (rojo oscuro). El ángulo que hace con la horizontal debe ser la mitad del ángulo entre ésta y el\(C\) vector. Eso es la mitad de 120 grados, o 60 grados. Como la suma de los ángulos interiores de un triángulo debe ser de 180 grados, esto significa que el tercer ángulo debe ser de 30 grados. La pata horizontal del triángulo (amarillo oscuro o tal vez “mostaza picante”) se puede determinar porque conocemos tanto la hipotenusa como el ángulo opuesto.

\[\text{opposite } = \text{ hypotenuse }\times \sin \theta \nonumber \]

El seno de 30 grados es exactamente 0.5, por lo tanto, la pata horizontal del triángulo debe ser 0.5 veces la magnitud de la unidad, o 0.5. Podemos usar el teorema de Pitágoras para encontrar la pata vertical restante (púrpura).

\[\text{vertical } = \sqrt{\text{hypotenuse}^2−\text{horizontal}^2} \nonumber \]

\[\text{vertical } = \sqrt{1^2−0.5^2} \nonumber \]

\[\text{vertical } = \sqrt{\frac{3}{4}} \nonumber \]

\[\text{vertical } = \frac{1}{2} \sqrt{3} \nonumber \]

La pata vertical se refleja perfectamente debajo del eje horizontal. Por lo tanto, el lapso de\(B\) a\(C\) debe ser el doble de este valor, o\(\sqrt{3}\). Como el voltaje desarrollado a través de cada rama del generador se conoce como el voltaje de fase del generador, podemos afirmar:

\[\text{The line voltage for a Y-connected generator is } \sqrt{3} \text{ times its phase voltage.} \label{9.1} \]

Por ejemplo, si el voltaje de fase de un generador conectado en Y es de 120 voltios, el voltaje de línea sería\(\sqrt{3}\) veces mayor, o aproximadamente 208 voltios.

Para un generador conectado delta, lo mismo se aplica a las corrientes de fase y línea, con la prueba dejada como ejercicio. Es decir,

\[\text{The line current for a delta-connected generator is } \sqrt{3} \text{ times its phase current.} \label{9.2} \]

Estas mismas relaciones se mantienen tanto para las cargas como para las fuentes, por ejemplo, la corriente en un tramo de una carga conectada en Y será la misma que la corriente de línea y su voltaje de fase será\(\sqrt{3}\) veces menor que el voltaje de línea.

\[\text{ In summation: For delta configurations (generator or load), the phase voltage is equal to the line voltage while the line current is larger than the phase current by } \sqrt{3} \text{. For Y configurations, the phase current is equal to the line current while the line voltage is } \sqrt{3} \text{ larger than the phase voltage.} \nonumber \]

Para sistemas homogéneos, como el generador y la carga comparten la misma configuración, los voltajes y corrientes de fase de la carga deben ser idénticos a los del generador. Una ayuda útil para la memoria es que la potencia disipada en el sistema debe ser igual a la potencia generada.

Ejemplo\(\PageIndex{1}\)

Un generador trifásico conectado en delta alimenta una carga trifásica conectada delta como el sistema que se muestra en la Figura\(\PageIndex{1}\). Suponga que el voltaje de fase del generador es 120 VCA RMS. La carga consta de tres patas idénticas de 50\( \Omega \) cada una. Determine el voltaje de línea, voltaje de fase de carga, corriente de fase del generador, corriente de línea, corriente de fase de carga y la potencia total entregada a la carga.

Al tratarse de un sistema homogéneo (delta-delta), el voltaje y la corriente de fase de carga son los mismos que los del generador. Por lo tanto, el voltaje de fase de carga también debe ser de 120 voltios. Segundo, en una configuración delta, el voltaje de línea es igual al voltaje de fase, nuevamente 120 voltios. La corriente de fase de carga se encuentra a través de la ley de Ohm y será un valor RMS porque el voltaje es RMS:

\[i_{phase} = \frac{v_{phase}}{Z_{load}} \nonumber \]

\[i_{phase} = \frac{120 V}{50 \Omega} \nonumber \]

\[i_{phase} = 2.4 A \nonumber \]

La corriente de fase del generador debe ser la misma porque el generador y la carga tienen la misma configuración. Para configuraciones delta, la corriente de línea es\(\sqrt{3}\) veces mayor que la corriente de fase, por lo tanto,

\[i_{line} = \sqrt{3}\times i_{phase} \nonumber \]

\[i_{line} = \sqrt{3}\times 2.4A \nonumber \]

\[i_{line} \approx 4.157A \nonumber \]

Finalmente, la potencia total se puede encontrar con una aplicación directa de la ley de potencia ya que la carga es puramente resistiva y tenemos valores RMS. Recuerda, esto es tres veces el poder disipado en una pierna.

\[P_{total} = 3\times {i_{phase}}^2 \times R \nonumber \]

\[P_{total} = 3\times (2.4 A)^2\times 50 \Omega \nonumber \]

\[P_{total} = 864 W \nonumber \]

Esto equivale a aproximadamente 1.2 HP. También podríamos haber calculado la potencia de fase de carga usando el voltaje de fase cuadrado dividido por la resistencia de carga, o multiplicando el voltaje de fase por la corriente de fase. Al tratarse de una carga puramente resistiva, no hay ángulo de fase, y por lo tanto no hay factor de potencia con el que preocuparnos.

Ejemplo\(\PageIndex{2}\)

Un generador trifásico conectado en Y alimenta una carga trifásica conectada en Y similar al sistema que se muestra en la Figura\(\PageIndex{2}\). Suponga que el voltaje de fase del generador es 220 VCA RMS. La carga consta de tres patas idénticas de 100\( \Omega \) cada una. Determine el voltaje de línea, voltaje de fase de carga, corriente de fase del generador, corriente de línea, corriente de fase de carga y la potencia total entregada a la carga.

Se trata de un sistema homogéneo (Y-Y), por lo tanto el voltaje y la corriente de fase de carga son los mismos que los del generador. En consecuencia, el voltaje de fase de carga debe ser de 220 voltios. En una configuración Y, el voltaje de línea es igual a los tiempos de voltaje de fase\(\sqrt{3}\).

\[v_{line} = \sqrt{3}\times v_{phase} \nonumber \]

\[v_{line} = \sqrt{3}\times 220V \nonumber \]

\[v_{line} \approx 381 V \nonumber \]

La corriente de fase de carga se encuentra a través de la ley de Ohm y será un valor RMS porque el voltaje es RMS. Esto es lo mismo que la corriente de fase del generador y también la corriente de línea.

\[i_{phase} = \frac{v_{phase}}{Z_{load}} \nonumber \]

\[i_{phase} = \frac{220 V}{100 \Omega} \nonumber \]

\[i_{phase} = 2.2A \nonumber \]

La potencia total se puede encontrar usando la ley básica de potencia ya que la carga es puramente resistiva y tenemos valores RMS. En este caso usaremos tiempos de corriente voltaje para un cambio de ritmo.

\[P_{total} = 3\times i_{phase} \times v_{phase} \nonumber \]

\[P_{total} = 3\times 2.2 A\times 220 V \nonumber \]

\[P_{total} = 1452 W \nonumber \]

Esto es apenas tímido de 2 HP. Una vez más, esta es una carga puramente resistiva y no hay ángulo de fase. Así, el factor de poder es la unidad con los poderes reales y aparentes siendo los mismos.

Ejemplo\(\PageIndex{3}\)

Para el sistema mostrado en la Figura\(\PageIndex{5}\), determinar la potencia aparente y real total entregada a la carga. También encuentra el voltaje de línea. El voltaje de fase de la fuente es de 240 voltios RMS a 60 Hz.

Figura\(\PageIndex{5}\): Circuito por Ejemplo\(\PageIndex{3}\).

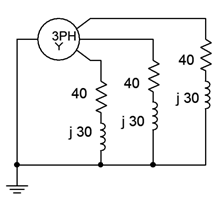
Dado que las tres patas de carga están todas juntas en un punto común (tierra), este debe ser un sistema Y-Y. En consecuencia, sabemos que el voltaje de línea debe ser\(\sqrt{3}\) multiplicado por el voltaje de fase del generador.

\[v_{line} = \sqrt{3}\times v_{phase} \nonumber \]

\[v_{line} = \sqrt{3}\times 240 V \nonumber \]

\[v_{line} \approx 416 V RMS \nonumber \]

Se trata de un sistema homogéneo (Y-Y) por lo que también sabemos que el voltaje de carga es igual al voltaje del generador, o 240 voltios RMS. A partir de eso podemos encontrar la corriente de carga (la corriente de línea debe ser del mismo valor porque se trata de una carga conectada en Y).

\[i_{phase} = \frac{v_{phase}}{Z_{load}} \nonumber \]

\[i_{phase} = \frac{240 V}{40+j 30 \Omega} \nonumber \]

\[i_{phase} = 4.8\angle −36.87^{\circ} A \nonumber \]

El ángulo de fase es apropiado para el generador de\(^{\circ}\) referencia 0. Los otros dos ángulos estarán fuera de esto por\(\pm\) 120\(^{\circ}\). La potencia aparente es simplemente el producto de las magnitudes de corriente y voltaje de carga.

\[S = 3\times i_{load} \times v_{load} \nonumber \]

\[S = 3\times 4.8A\times 240V \nonumber \]

\[S = 3456 VA \nonumber \]

El poder real se puede encontrar de varias maneras diferentes:

\[P = S\times \cos \theta \nonumber \]

\[P = 3456 VA \times \cos (−36.87^{\circ}) \nonumber \]

\[P = 2765 W \nonumber \]

\[P = 3\times {i_{load}}^2\times R_{load} \nonumber \]

\[P = 3\times 4.8A 2\times 40 \Omega \nonumber \]

\[P = 2765W \nonumber \]

Simulación por Computadora

El circuito de Ejemplo\(\PageIndex{3}\) es digno de una simulación. Lo primero que hay que hacer es determinar un valor apropiado de inductancia para lograr una reactancia de\(j40 \Omega \). Dada la frecuencia de fuente de 60 Hz, ésta resulta ser aproximadamente de 80 mH. El circuito se construye como se muestra en la Figura\(\PageIndex{6}\). El voltaje de fase fuente RMS de 240 voltios es equivalente a aproximadamente 340 voltios pico. Las posiciones del inductor y la resistencia en cada pata se han intercambiado por una razón que será evidente en breve.

Figura\(\PageIndex{6}\): El sistema equivalente de la Figura\(\PageIndex{5}\) en un simulador.

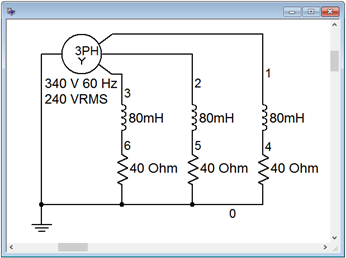
El punto de interés inmediato es verificar los cambios de tiempo y amplitudes de los voltajes de fase. Estos corresponden a los nodos 1, 2 y 3. En esta configuración, el voltaje de fase de carga es igual al voltaje de fase del generador, por lo que deben ser de 340 voltios pico y separados por 120 grados o 1/3rd de un ciclo.

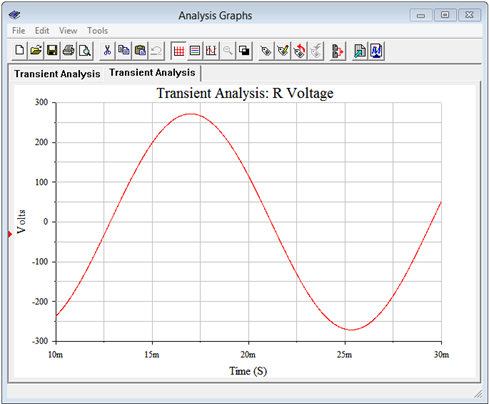
Se realiza un análisis transitorio, trazando los voltajes de los nodos de interés. El resultado se muestra en la Figura\(\PageIndex{7}\). Los voltajes son precisamente los esperados y la gráfica se compara perfectamente con la gráfica teórica de la Figura 9.2.4.

Figura\(\PageIndex{7}\): Los tres voltajes de carga simulados a partir de la Figura\(\PageIndex{6}\).

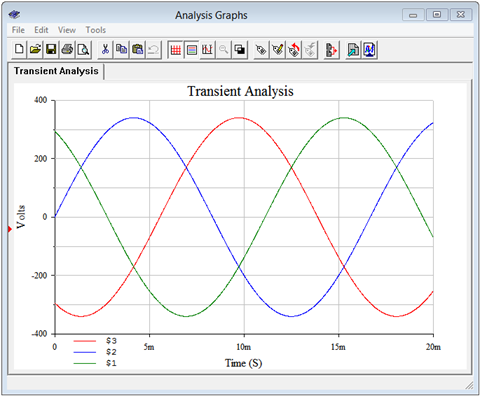
Ahora comprobamos el voltaje de la línea. Esto se calculó para ser 416 voltios RMS, o aproximadamente 588 voltios pico. El postprocesador se utiliza para mostrar el resultado del voltaje del nodo 1 menos el voltaje del nodo 2. Esto se muestra en la Figura\(\PageIndex{8}\). Nuevamente, los resultados son los esperados con un pico poco menos de 600 voltios.

Por último, investigaremos la verdadera potencia de carga. Quizás la forma más fácil de hacerlo es determinar el voltaje a través de la porción resistiva de la carga. De trabajos previos sabemos que el verdadero poder solo está asociado a la resistencia, no a la reactancia. Por lo tanto, todo lo que necesitamos hacer es medir el voltaje pico a través de la resistencia. A partir de ahí, encontramos su equivalente RMS, lo cuadramos y dividimos por el valor de la resistencia. Esto nos da la verdadera potencia de carga en una pierna. Para la potencia total simplemente triplicamos el resultado. Obtener el voltaje a través de la resistencia es fácil si la resistencia está conectada a tierra. En ese caso, es solo el voltaje en el nodo al que está conectada la resistencia. Es por ello que las posiciones del inductor y la resistencia se intercambiaron en la simulación. Al estar en serie, no hace diferencia en la impedancia de carga global, sin embargo, la nueva disposición nos permite obtener el voltaje de la resistencia directamente en lugar de tener que depender de un voltaje diferencial obtenido a través del postprocesador.

Se realiza otro análisis transitorio, esta vez trazando el voltaje a través de una de las resistencias de carga; a saber, el nodo 4. El resultado se muestra en la Figura\(\PageIndex{9}\). El pico de esta forma de onda se mide para ser 271.5 voltios, o alrededor de 192 voltios RMS. Al cuadrar esto y dividirlo por 40\( \Omega \) rinde un poco más de 921 watts por pierna, para un total de aproximadamente 2765 vatios, como se esperaba.

Figura\(\PageIndex{8}\): Una de las tensiones de línea simuladas a partir de la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{9}\): Voltaje simulado en una de las resistencias de carga de la Figura\(\PageIndex{6}\).

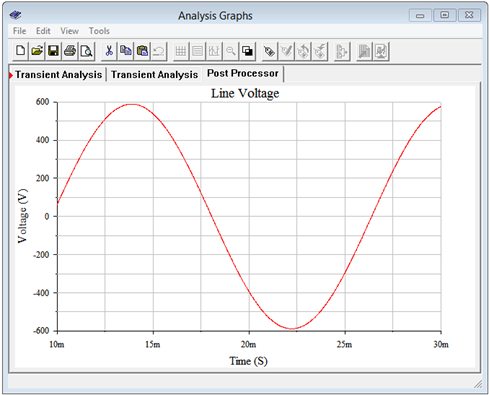
Sistemas Heterogéneos

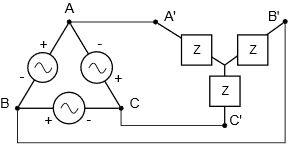
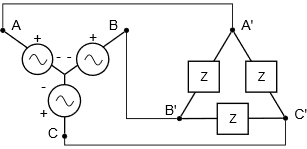
Los sistemas configurados como Delta a Y y A-Delta parecen ser un poco más complejos que los sistemas homogéneos. Nos referiremos a estos como sistemas heterogéneos ya que las estructuras del generador y la carga son de tipo opuesto. Los ejemplos se muestran en las Figuras\(\PageIndex{10}\) y\(\PageIndex{11}\), respectivamente.

Figura\(\PageIndex{10}\): Un generador conectado delta con una carga conectada en Y (delta-Y).

Figura\(\PageIndex{11}\): Un generador conectado en Y con una carga delta conectada (Ydelta).

Estos sistemas no son tan difíciles como piensan algunas personas; todo lo que tienes que hacer es recordar declaraciones\ ref {9.1} y\ ref {9.2}. En efecto, vale la pena repetir aquí la suma:

\ text {Para configuraciones delta (generador o carga), el voltaje de fase es igual al voltaje de línea mientras que la corriente de línea es mayor que la corriente de fase por}\ sqrt {3}\ text {. Para configuraciones Y, la corriente de fase es igual a la corriente de línea mientras que el voltaje de línea es}\ sqrt {3}\ text {mayor que el voltaje de fase.} \ nonumber\]

Se puede pensar en analizar estos sistemas como un proceso de dos pasos. Primero, determinar el voltaje de línea y la corriente del generador o de la carga; y segundo, la transición de la línea al otro lado (carga o generador). Si se produce confusión, recuerde que la energía generada debe ser igual a la potencia disipada o entregada.

En la Figura\(\PageIndex{10}\), el voltaje de línea es igual al voltaje de fase del generador. La carga es Yconnected, por lo que cada tramo ve el voltaje de línea dividido por\(\sqrt{3}\). En base a esto, se puede calcular cada tramo de la corriente de carga. Observe que la corriente de línea es igual a la corriente de carga. La corriente de fase del generador será la corriente de línea dividida por\(\sqrt{3}\).

En la Figura\(\PageIndex{11}\), el voltaje de línea es igual a\(\sqrt{3}\) veces el voltaje de fase del generador. La carga está conectada delta, por lo que cada pata ve el voltaje de la línea. Sabiendo esto, se puede calcular cada tramo de la corriente de carga. Además, la corriente de línea es igual a la corriente de fase del generador, y la corriente de fase de carga será igual a la corriente de línea dividida por\(\sqrt{3}\).

Ejemplo\(\PageIndex{4}\)

Un sistema delta-Y como el que se muestra en la Figura\(\PageIndex{10}\) tiene un voltaje de fase del generador de 230 voltios RMS a 50 Hz. Si la carga es\(200\angle 0^{\circ}\)\( \Omega \), determine la corriente de fase del generador, la tensión de línea, la tensión de fase de carga, la corriente de fase de carga y la potencia total entregada a la carga.

El generador está conectado delta por lo que el voltaje de línea es igual al voltaje de fase del generador, o 230 voltios. La carga, al estar conectada en Y, verá un voltaje de fase que se reduce en un factor de\(\sqrt{3}\).

\[v_{load} = \frac{v_{line}}{\sqrt{3}} \nonumber \]

\[v_{load} = \frac{230 V}{\sqrt{3}} \nonumber \]

\[v_{load} \approx 132.8V RMS \nonumber \]

Podemos usar la ley de Ohm para determinar la corriente de fase de carga.

\[i_{load} = \frac{v_{phase}}{Z_{load}} \nonumber \]

\[i_{load} = \frac{132.8 V}{200\angle 0^{\circ} \Omega} \nonumber \]

\[i_{load} \approx 0.664 A RMS \nonumber \]

Al estar conectada en Y, la corriente de línea debe ser la misma que la corriente de fase de carga, o 0.664 amperios. Para conexiones delta, la corriente de línea es\(\sqrt{3}\) veces mayor que la corriente de fase, por lo tanto, la corriente de fase del generador debe ser\(\sqrt{3}\) veces menor.

\[i_{gen} = \frac{i_{line}}{\sqrt{3}} \nonumber \]

\[i_{gen} = \frac{0.664A}{\sqrt{3}} \nonumber \]

\[i_{gen} \approx 0.383A RMS \nonumber \]

La carga es puramente resistiva y tenemos valores RMS por lo que la potencia total se puede encontrar a través de la ley de potencia (la potencia aparente es igual a la potencia verdadera en este caso).

\[P_{total} = 3\times {i_{load}}^2 \times R \nonumber \]

\[P_{total} = 3\times (0.664A)^2 \times 200 \Omega \nonumber \]

\[P_{total} = 264 W \nonumber \]

Como comprobación cruzada, la potencia generada es:

\[P_{total} = 3\times i_{gen} \times v_{gen} \nonumber \]

\[P_{total} = 3\times 0.383A\times 230 V \nonumber \]

\[P_{total} = 264 W \nonumber \]

La energía generada equivale a la potencia disipada.

Ejemplo\(\PageIndex{5}\)

Un sistema Y-delta como el que se muestra en la Figura\(\PageIndex{11}\) tiene un voltaje de fase del generador de 100 voltios RMS a 60 Hz. Si la carga tiene una magnitud de 50\( \Omega \) con un factor de potencia de retardo de 0.8, determine la corriente de fase del generador, la tensión de línea, la tensión de fase de carga, la corriente de fase de carga y la potencia real total entregada a la carga.

El generador conectado en Y crea un voltaje de línea igual a los tiempos de voltaje de fase del generador\(\sqrt{3}\). Este es también el voltaje de fase de carga ya que está conectado delta.

\[v_{line} = \sqrt{3}\times v_{phase} \nonumber \]

\[v_{line} = \sqrt{3}\times 100 V \nonumber \]

\[v_{line} \approx 173.2V RMS \nonumber \]

La carga delta-conectada verá un voltaje de fase que es el mismo que el voltaje de línea, o 173.2 voltios. A partir de esto podemos determinar la corriente de carga.

\[i_{load} = \frac{v_{phase}}{Z_{load}} \nonumber \]

\[i_{load} = \frac{173.2V}{50 \Omega} \nonumber \]

\[i_{load} \approx 3.464A RMS \nonumber \]

Como la carga está conectada delta, la corriente de línea es los tiempos de corriente de carga\(\sqrt{3}\). La corriente de fase del generador será la misma que la corriente de línea.

\[i_{line} = \sqrt{3}\times i_{phase} \nonumber \]

\[i_{line} = \sqrt{3}\times 3.464A \nonumber \]

\[i_{line} = 6 A RMS \nonumber \]

La verdadera potencia de carga se puede encontrar de varias maneras. Primero, podemos usar el\(i^2 R\) formulario. Para ello necesitamos encontrar la porción resistiva de la carga. Recordemos que el factor de potencia es igual al coseno\(\theta\). Por lo tanto, el ángulo de impedancia es:

\[\theta = \cos^{−1} PF \nonumber \]

\[\theta = \cos^{−1} 0.8 \nonumber \]

\[\theta \approx 36.9^{\circ} \nonumber \]

La parte real es:

\[R = Z \cos \theta \nonumber \]

\[R = 50 \Omega \cos 36.9^{\circ} \nonumber \]

\[R = 40 \Omega \nonumber \]

Como alternativa, podríamos haber multiplicado\(Z\) por\(PF\) para obtener esto. Continuando:

\[P_{total} = 3\times {i_{load}}^2 \times R \nonumber \]

\[P_{total} = 3\times (3.464 A)^2\times 40 \Omega \nonumber \]

\[P_{total} = 1440 W \nonumber \]

También podríamos encontrar el poder aparente y usar el factor de potencia.

\[P_{total} = 3\times v_{load} \times i_{load} PF \nonumber \]

\[P_{total} = 3\times 173.2V\times 3.464 A\times 0.8 \nonumber \]

\[P_{total} = 1440 W \nonumber \]

Como comprobación cruzada, compare la potencia disipada con la energía generada.

\[P_{total} = 3\times v_{gen}\times i_{gen}\times PF \nonumber \]

\[P_{total} = 3\times 100V\times 6A\times 0.8 \nonumber \]

\[P_{total} = 1440 W \nonumber \]