1.1: Ingeniería de RF y Microondas

Las radiocomunicaciones son el principal impulsor del desarrollo del sistema de RF, lo que lleva a la evolución de la tecnología de RF a un ritmo sin precedentes Una señal de radio es una señal que se genera de manera coherente, radiada por una antena transmisora, se propaga a través del aire, se recoge por una antena receptora, y luego se amplifica y se extrae información. El espectro radioeléctrico es parte del espectro electromagnético (EM) explotado por los humanos para las comunicaciones. En la Tabla se muestra una amplia categorización del espectro EM\(\PageIndex{1}\). Hoy en día las radios operan desde\(3\text{ Hz}\) (para comunicaciones submarinas) hasta\(300\text{ GHz}\) (propuestas para comunicaciones celulares 6G).

Nombre o banda	Frecuencia	Longitud de onda
Radiofrecuencia	\(3\text{ Hz} - 300\text{ GHz}\)	\(100,000\text{ km} - 1\text{ mm}\)
Microondas	\(300\text{ MHz} - 300\text{ GHz}\)	\(1\text{ m} - 1\text{ mm}\)
\(\text{mm}\)Banda milimétrica	\(110-300\text{ GHz}\)	\(2.7\text{mm} - 1.0\text{ mm}\)
Infrarrojos	\(300\text{ GHz} - 400\text{ THz}\)	\(1\text{ mm} - 750\text{ nm}\)
Infrarrojos lejanos	\(300\text{ GHz} - 20\text{ THz}\)	\(1\text{ mm} - 15\:\mu\text{m}\)
Infrarrojos de larga onda	\(20\text{ THz} - 37.5\text{ THz}\)	\(15 - 8\:\mu\text{m}\)
infrarrojo de longitud de onda media	\(37.5 - 100\text{ THz}\)	\(8- 3\:\mu\text{m}\)
Infrarrojos de onda corta	\(100\text{ THz} - 214\text{ THz}\)	\(3 - 1.4\:\mu\text{m}\)
Infrarrojos cercanos	\(214\text{ THz} - 400\text{ THz}\)	\(1.4\:\mu\text{m} - 750\text{ nm}\)
Visible	\(400\text{ THz} - 750\text{ THz}\)	\(750 - 400\text{ mm}\)
Ultravoilet	\(750\text{ THz} - 30\text{ PHz}\)	\(400 - 10\text{ nm}\)
Rayos X	\(30\text{ PHz} - 30\text{ EHz}\)	\(10- 0.01\text{ nm}\)
Rayos Gamma	\(> 15\text{ EHz}\)	\(< 0.02\text{ nm}\)
Gigahercios,\(\text{GHz} = 109\text{ Hz}\); terahercios,\(\text{THz} = 1012\text{ Hz}\); pentahercios,\(\text{PHz} = 1015\text{ Hz}\); exahercios,\(\text{EHz} = 1018\text{ Hz}\).

Cuadro\(\PageIndex{1}\): Divisiones de amplio espectro electromagnético.

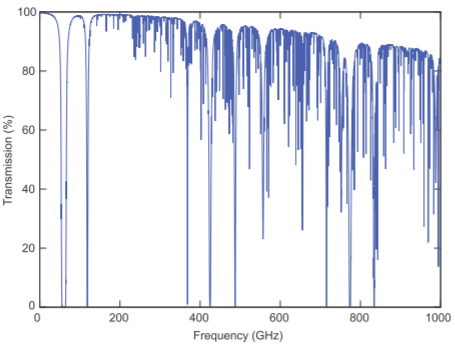
Figura\(\PageIndex{1}\):: Transmisión atmosférica en Mauna Kea, con una altura de\(4.2\text{ km}\), en la Isla de Hawai donde la presión atmosférica es\(60\%\) de la que se encuentra a nivel del mar y el aire es seco con un nivel de vapor de agua precipitable de\(0.001\text{ mm}\). Después [1].

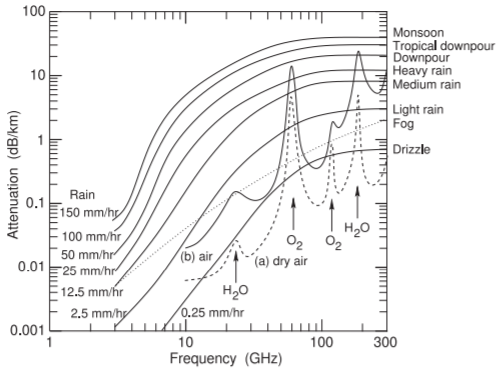
Figura\(\PageIndex{2}\): Exceso de atenuación por condiciones atmosféricas que muestran el efecto de la lluvia sobre la transmisión de RF a nivel del mar. La curva (a) es la atenuación atmosférica, debido a la excitación de resonancias moleculares, de aire muy seco en\(0^{\circ}\text{C}\), la curva (b) es para el aire típico (es decir, menos seco) a\(20^{\circ}\text{C}\). La atenuación mostrada para niebla y lluvia es adicional (in\(\text{dB}\)) a la absorción atmosférica mostrada como curva (b).

Las señales de RF que se propagan en el aire son absorbidas por moléculas en la atmósfera principalmente por resonancias moleculares como la flexión y estiramiento de enlaces que convierten la energía EM en calor. La transmitancia de señales de radio versus frecuencia en aire seco a una altitud de\(4.2\text{ km}\) se muestra en la Figura\(\PageIndex{1}\) y hay muchos agujeros de transmisión debido a resonancias moleculares. La resonancia molecular de menor frecuencia en el aire seco es la resonancia de oxígeno centrada en\(60\text{ GHz}\), pero por debajo de ella la absorción en el aire seco es muy pequeña. La atenuación aumenta con una mayor presión de vapor de agua que alcanza su punto máximo\(22\text{ GHz}\) y se ensancha debido al empaquetamiento cercano de las moléculas en el aire. El efecto del agua se ve en la Figura\(\PageIndex{2}\) y se observa que la lluvia y el vapor de agua tienen poco efecto en las comunicaciones celulares que están por debajo,\(5\text{ GHz}\) excepto para 5G de onda milimétrica.

Las señales de RF se difractan y así pueden doblarse alrededor de las estructuras y penetrar en los valles. La capacidad de difractar se reduce al aumentar la frecuencia. Sin embargo, a medida que aumenta la frecuencia, el tamaño de las antenas disminuye y la capacidad de transportar información aumenta. Un muy buen compromiso para las comunicaciones móviles es en UHF,\(300\text{ MHz}\) a\(4\text{ GHz}\), donde las antenas son de tamaño conveniente y hay una buena capacidad para difractar alrededor de objetos e incluso penetrar paredes.

1.1.1 Campos electromagnéticos

Comunicarse mediante señales EM construidas a partir de una comprensión de la inducción magnética basada en los experimentos de Faraday en 1831 [2] en los que investigó la relación de los campos magnéticos y las corrientes, y ahora conocida como la ley de Faraday. Esta y las otras leyes de campo estáticas no son suficientes para describir las ondas de radio. La descripción requerida está plasmada en las ecuaciones de Maxwell y después de que éstas se desarrollaron tomó poco tiempo antes de que se inventara la radio.

1.1.2 Leyes de campo estáticas

Hay dos componentes del campo EM, el campo eléctrico,\(E\), con unidades de voltios por metro (\(\text{V/m}\)), y el campo magnético,\(H\), con unidades de amperios por metro (\(\text{A/m}\)). También hay dos cantidades de flujo siendo el primero\(D\), la densidad de flujo eléctrico, con unidades de culombios por metro cuadrado (\(\text{C/m}^{2}\)), y el otro es\(B\), la densidad de flujo magnético, con unidades de teslas (\(\text{T}\)). \(B\)y\(H\), y\(D\) y\(E\), se relacionan entre sí por las propiedades del medio, que se plasman en las cantidades\(\mu\) y\(\varepsilon\) (con la letra caligráfica, por ejemplo\(\mathcal{B}\), denotando una cantidad de dominio de tiempo):

\[\label{eq:1}\overline{\mathcal{B}}=\mu\overline{\mathcal{H}} \]

\[\label{eq:2}\overline{\mathcal{D}}=\varepsilon\overline{\mathcal{E}} \]

donde la barra superior denota una cantidad de vector, y\(\mu\) es la permeabilidad del medio y describe la capacidad de almacenar energía magnética en una región. La permeabilidad en el espacio libre (o vacío) es\(\mu_{0}=4\pi\times 10^{-7}\text{ H/m}\) y luego

\[\label{eq:3}\overline{\mathcal{B}}=\mu_{0}\overline{\mathcal{H}} \]

La otra cantidad de material es la permitividad,\(\varepsilon\), y en un vacío

\[\label{eq:4}\overline{\mathcal{D}}=\varepsilon_{0}\overline{\mathcal{E}} \]

donde\(\varepsilon_{0} = 8.854\times 10^{-12}\text{ F/m}\) está la permitividad de un vacío. La permitividad relativa\(\varepsilon_{r}\), la permeabilidad relativa,\(\mu_{r}\), se definen como

\[\label{eq:5}\varepsilon_{r}=\varepsilon /\varepsilon_{0}\qquad\text{and}\qquad\mu_{r}=\mu /\mu_{0} \]

Ley Biot-Savart

La ley Biot-Savart relaciona la corriente con el campo magnético como, ver Figura 1-3,

\[\label{eq:6}d\overline{H} = \frac{Id\ell\times\hat{a}_{R}}{4\pi R^{2}} \]

con unidades de amperios por metro en el sistema SI. En Ecuación\(\eqref{eq:6}\)\(d\overline{H}\) está el\(H\) campo estático incremental,\(I\) es actual,\(d\ell\) es el vector de la longitud de un filamento de corriente\(I\),\(\hat{a}_{R}\) es el vector unitario en la dirección del filamento actual al campo magnético, y\(R\) es la distancia entre el filamento y el campo magnético. El\(d\overline{H}\) campo se dirige en ángulo recto hacia\(\hat{a}_{R}\) y el filamento actual. Entonces Ecuación\(\eqref{eq:6}\) dice que un filamento de corriente produce un

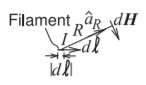
Figura\(\PageIndex{3}\): Diagrama que ilustra la ley Biot-Savart. La ley relaciona un filamento estático de corriente con el\(H\) campo incremental a distancia.

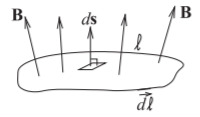
Figura\(\PageIndex{4}\): Diagrama que ilustra la ley de Faraday. El contorno\(\ell\) encierra la superficie.

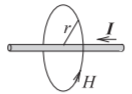
Figura\(\PageIndex{5}\): Diagrama que ilustra la ley de Ampere. La ley de Ampere relaciona la corriente,\(I\), en un cable con el campo magnético que lo rodea,\(H\).

campo magnético en un punto. El campo magnético total de una corriente en un alambre o superficie se puede encontrar modelando el alambre o superficie como una serie de filamentos de corriente, y el campo magnético total en un punto se obtiene integrando las contribuciones de cada filamento.

Ley de Inducción de Faraday

La ley de Faraday relaciona un campo magnético variable en el tiempo con una caída de voltaje inducida\(V\), alrededor de un camino cerrado, que ahora se entiende como\(\oint_{\ell}\overline{\mathcal{E}}\cdot d\ell\), es decir, el contorno cerrado integral del campo eléctrico,

\[\label{eq:7}V=\oint_{\ell}\overline{\mathcal{E}}\cdot d\ell = -\oint_{s}\frac{\partial\overline{\mathcal{B}}}{\partial t}\cdot d\text{s} \]

y esto tiene las unidades de voltios en el sistema de unidades SI. La operación descrita en la Ecuación\(\eqref{eq:7}\) se ilustra en la Figura\(\PageIndex{4}\).

Ley Circuital de Ampere

La ley circuital de Ampere, a menudo llamada solo ley de Ampere, relaciona la corriente continua y el campo magnético estático\(\overline{\mathcal{H}}\), ver Figura\(\PageIndex{5}\):

\[\label{eq:8}\oint_{\ell}\overline{H}\cdot d\ell = I_{\text{enclosed}} \]

Es decir, la integral del campo magnético alrededor de un bucle es igual a la corriente encerrada por el bucle. Usando simetría, la magnitud del campo magnético a una\(r\) distancia del centro del cable que se muestra en la Figura\(\PageIndex{5}\) es

\[\label{eq:9}H=|I|/(2\pi r) \]

Ley de Gauss

La ley final de EM estática es la ley de Gauss, que relaciona el vector de densidad de flujo eléctrico estático,\(\overline{D}\), con la carga. Con referencia a la Figura\(\PageIndex{6}\), la ley de Gauss en forma integral es

\[\label{eq:10}\oint_{s}\overline{D}\cdot d\text{s}=\int_{v}\rho_{v}\cdot dv=Q_{\text{enclosed}} \]

Esto establece que la integral del vector de flujo eléctrico constante,\(\overline{D}\), sobre una superficie cerrada es igual a la carga total encerrada por la superficie,\(Q_{\text{enclosed}}\).

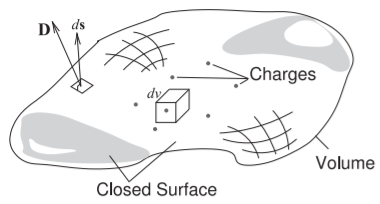
Figura\(\PageIndex{6}\): Diagrama que ilustra la ley de Gauss. Las cargas se distribuyen en el volumen encerrado por la superficie cerrada. Un área incremental es descrita por el vector\(d\text{s}\), que es normal a la superficie y cuya magnitud es el área del área incremental.

Ley del magnetismo de Gauss

La ley del magnetismo de Gauss es paralela a la ley de Gauss que se aplica a los campos eléctricos y cargas. En forma integral la ley es

\[\label{eq:11}\oint_{s}\overline{B}\cdot d\text{s}=0 \]

Esto establece que la integral del vector de flujo magnético constante,\(\overline{D}\), sobre una superficie cerrada es cero reflejando el hecho de que no existen cargas magnéticas.

1.1.3 Ecuaciones de Maxwell

El paso esencial en la invención de la radio fue el desarrollo de las ecuaciones de Maxwell en 1861. Antes de que se postularan las ecuaciones de Maxwell, se conocían varias leyes estáticas EM. Tomados en conjunto, no pueden describir la propagación de las señales EM, pero pueden derivarse de las ecuaciones de Maxwell. Las ecuaciones de Maxwell no pueden derivarse de las leyes de campo magnético y eléctrico estático. Las ecuaciones de Maxwell encarnan una visión adicional que relaciona las derivadas espaciales con las derivadas del tiempo, lo que lleva a una descripción de los campos de propagación. Las ecuaciones de Maxwell son

\[\label{eq:12}\nabla\times\overline{\mathcal{E}}=-\frac{\partial\overline{\mathcal{B}}}{\partial t}-\overline{\mathcal{M}} \]

\[\label{eq:13}\nabla\cdot\overline{\mathcal{D}}=\rho_{V} \]

\[\label{eq:14}\nabla\times\overline{\mathcal{H}}=\frac{\partial\overline{\mathcal{D}}}{\partial t}+ \overline{\mathcal{J}} \]

\[\label{eq:15}\nabla\cdot\overline{\mathcal{B}}=\rho_{mV} \]

Las cantidades adicionales en Ecuaciones\(\eqref{eq:12}\) -\(\eqref{eq:15}\) son

• \(\overline{\mathcal{J}}\), la densidad de corriente eléctrica, con unidades de amperios por metro cuadrado (\(\text{A/m}^{2}\));
• \(\rho_{V}\), la densidad de carga eléctrica, con unidades de culombios por metro cúbico (\(\text{C/m}^{3}\));
• \(\rho_{mV}\), la densidad de carga magnética, con unidades de webers por metro cúbico (\(\text{Wb/m}^{3}\)); y
• \(\overline{\mathcal{M}}\), la densidad de corriente magnética, con unidades de voltios por metro cuadrado (\(\text{V/m}^{2}\)).

Las cargas magnéticas no existen, pero su introducción a través de la densidad de carga magnética\(\rho _{mV}\), y la densidad de corriente magnética\(\overline{\mathcal{M}}\), introducen una simetría estéticamente atractiva a las ecuaciones de Maxwell. Las ecuaciones de Maxwell son ecuaciones diferenciales, y como ocurre con la mayoría de las ecuaciones diferenciales, su solución se obtiene con condiciones de límite particulares, que en la ingeniería de radio son impuestas por conductores.

Las ecuaciones de Maxwell tienen tres tipos de derivadas. Primero, está la derivada del tiempo,\(\partial /\partial t\). Luego hay dos derivadas espaciales, llamadas curl\(\nabla\times\), capturando la forma en que un campo circula espacialmente (o la cantidad que se acurruca sobre sí mismo)\(\nabla\cdot\), y, llamado operador div, que describen la extensión de un

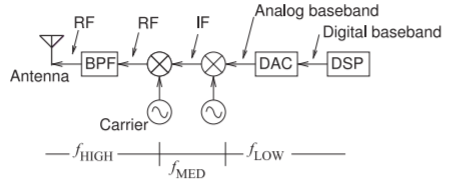
Figura\(\PageIndex{7}\): Un transmisor simple con secciones de baja\(f_{\text{LOW}}\)\(f_{\text{MED}}\), media y alta frecuencia.\(f_{\text{HIGH}}\) Los mezcladores pueden idealizarse como multiplicadores que aumentan la frecuencia de la banda base de entrada o señal IF por la frecuencia de la portadora.

campo. En coordenadas rectangulares, curl,\(\nabla\times\), describe cuánto circunda un campo alrededor de los\(z\) ejes\(x,\: y,\) y. Es decir, el rizo describe cómo un campo circula sobre sí mismo. Entonces Ecuación\(\eqref{eq:12}\) relaciona la cantidad que un campo eléctrico circula sobre sí mismo con los cambios del\(B\) campo en el tiempo. Entonces una derivada espacial de los campos eléctricos está relacionada con una derivada temporal del campo magnético. También en Ecuación\(\eqref{eq:14}\) la derivada espacial del campo magnético está relacionada con la derivada temporal del campo eléctrico. Estos son los elementos clave que dan como resultado una propagación autosustentable.

Div\(\nabla\cdot\),, describe cómo se extiende un campo desde un punto. La rapidez con que un campo varía con el tiempo,\(\partial\overline{\mathcal{B}}/\partial t\) y\(\partial\overline{\mathcal{D}}/\partial t\), depende de la frecuencia. Las derivadas más interesantes son\(\nabla\times\overline{\mathcal{E}}\) y\(\nabla\times\overline{\mathcal{H}}\) que describen qué tan rápido un campo puede cambiar espacialmente, esto depende de la longitud de onda relativa a la geometría. Si las dimensiones de la sección transversal de una línea de transmisión son menores que una longitud de onda (\(\lambda /2\)o\(\lambda /4\) en diferentes circunstancias cuando hay conductores), entonces será imposible que los campos se acurruquen sobre sí mismos y así solo habrá una solución (sin variación o mínima variación del \(E\)y\(H\) campos) o, en algunos casos, ninguna solución a las ecuaciones de Maxwell.