8.3: Gráfico Smith
- Page ID
- 81675
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El gráfico Smith es una poderosa herramienta gráfica y dominar el gráfico Smith es esencial para ingresar al mundo del diseño de circuitos de RF y microondas ya que todos los practicantes usan esto como si fuera bien entendido por otros. Se necesita esfuerzo para dominar pero fundamentalmente es bastante simple combinar una trama polar utilizada para
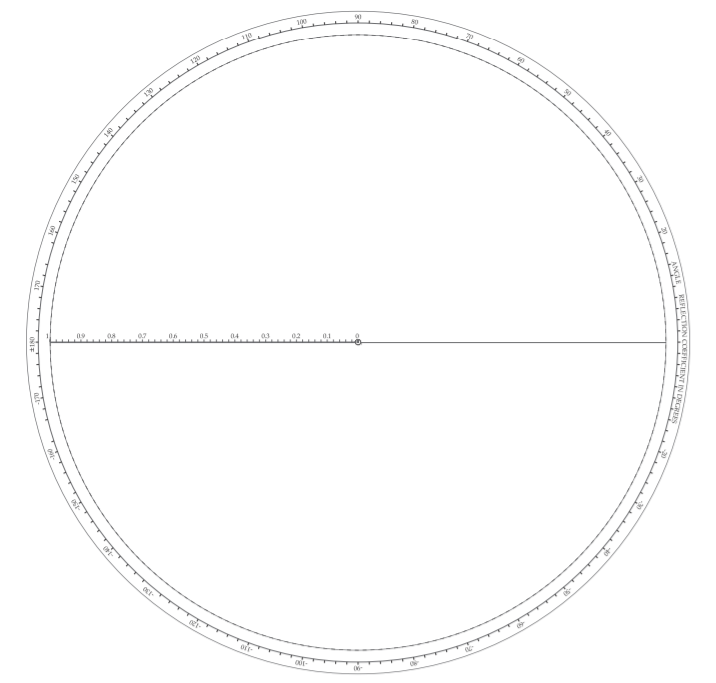
Figura\(\PageIndex{1}\): Gráfico polar para trazar el coeficiente de reflexión y el coeficiente de transmisión.
trazando\(S\) parámetros directamente, curvas que permiten representar directamente impedancias y admitancias normalizadas, y escalas que permiten leer longitudes eléctricas en términos de longitudes de onda y grados. El gráfico tiene muchos números impresos en fuente bastante pequeña y con letreros dejados ya que hay espacio limitado.
El gráfico de Smith fue inventado por Phillip Smith y presentado en forma cercana a su forma actual en 1937, véase [1, 2, 3, 4]. Una vez los nomógrafos y las calculadoras gráficas fueron herramientas comunes de ingeniería principalmente debido a los limitados recursos informáticos. Solo unos pocos han sobrevivido en el uso de ingeniería eléctrica, siendo abrumadoramente los gráficos de Smith los más importantes.
Esta sección presenta primero el gráfico Smith de impedancia y luego el gráfico Smith de admisión antes de introducir un gráfico Smith combinado que es la forma necesaria en el diseño. Se presentan una serie de ejemplos a
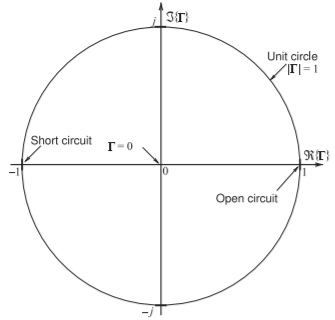
Figura\(\PageIndex{2}\): Gráfica polar anotada del coeficiente de reflexión con ejes reales e imaginarios.\(Re\)\(ℑ\) Se indica el cortocircuito\(\Gamma = −1\) y el circuito\(\Gamma = +1\) abierto. El coeficiente de reflexión se refiere a una impedancia de referencia\(Z_{REF}\). Así una impedancia\(Z_{L}\) tiene el coeficiente de reflexión\(\Gamma =(Z_{L} − Z_{REF})/(Z_{L} + Z_{REF})\). Una observación interesante es que el ángulo de\(\Gamma\) cuándo\(Z_{L}\) es inductivo, es decir, tiene una reactancia positiva, tiene un ángulo positivo entre\(0^{\circ}\)\(180^{\circ}\) y y así\(\Gamma\) está en la mitad superior de la gráfica polar. De manera similar el ángulo de\(\Gamma\) cuando\(Z_{L}\) es capacitivo, es decir, tiene una reactancia negativa, tiene un ángulo negativo entre\(0^{\circ}\)\(−180^{\circ}\) y y así\(\Gamma\) está en la mitad inferior de la gráfica polar.
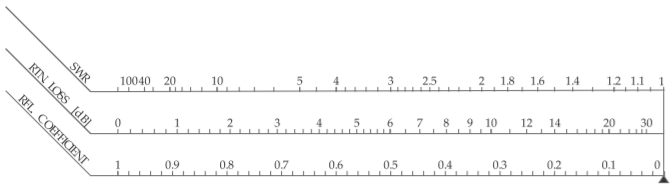
Figura\(\PageIndex{3}\): Nomógrafo que relaciona el coeficiente de reflexión (RFL. COFICIENTE),\(\rho\); la pérdida de retorno (RTN. PÉRDIDA) (en decibelios); y la relación de onda estacionaria (SWR).
ilustran cómo se lee y se usa un gráfico de Smith para implementar diseños simples. El gráfico Smith presenta una gran cantidad de información en un espacio confinado y se requiere interpretación, como la aplicación de signos apropiados, para extraer valores. El gráfico Smith es una herramienta “posterior del sobre” que los diseñadores de circuitos de RF y microondas utilizan para esbozar diseños.
8.3.1 Impedancia Smith
El coeficiente de reflexión\(\Gamma\),, está relacionado con una carga,\(Z_{L}\), por
\[\label{eq:1}\Gamma=\frac{Z_{L}-Z_{REF}}{Z_{L}+Z_{REF}} \]
donde\(Z_{REF}\) está la impedancia de referencia del sistema. Con la impedancia de carga normalizada\(z_{l} = r + \jmath x = Z_{L}/Z_{REF}\), esto se convierte
\[\label{eq:2}\Gamma=\frac{r+\jmath x-1}{r+\jmath x+1} \]
Comúnmente en el diseño de red, los elementos reactivos se agregan ya sea en derivación o en serie a una red existente. Si se agrega un elemento reactivo en serie entonces la reactancia de entrada,\(x\), se cambia mientras que la resistencia de entrada,\(r\), se mantiene constante. Por lo tanto, superponer los loci de\(\Gamma\) (sobre el\(S\) parámetro gráfico polar) con valores fijos de\(r\), pero valores variables de\(x\) (\(x\)variando de\(−∞\) a\(∞\)), resulta útil, como se verá. También es útil trazar los loci de\(\Gamma\) con valores fijos de\(x\) y valores\(r\) variables de\(r\) (variando de\(0\) a\(∞\)). La combinación de las gráficas polares de reflexión/transmisión, los nomógrafos y los\(x\) loci\(r\) y se denomina gráfico Smith de impedancia, ver Figura\(\PageIndex{5}\). Esta sigue siendo una gráfica polar del coeficiente de reflexión y los arcos y círculos de constante y resistencia permiten una fácil conversión entre el coeficiente de reflexión y la impedancia.
La gráfica Smith de impedancia completa mostrada en la Figura\(\PageIndex{5}\) es desalentadora, por lo que la discusión comenzará con la forma menos densa de la gráfica Smith de impedancia mostrada en la Figura\(\PageIndex{6}\) (a) que se anota en la Figura\(\PageIndex{6}\) (b). Haciendo referencia a la Figura\(\PageIndex{6}\) (b), el círculo unitario corresponde a una magnitud de coeficiente de reflexión de uno y por lo tanto una reactancia pura. Obsérvese que existen líneas de resistencia constante y arcos de reactancia constante. Todos los puntos de la mitad superior del gráfico Smith tienen reactancias positivas y por lo tanto todos los puntos de coeficiente de reflexión trazados en la mitad superior del gráfico Smith indican impedancias inductivas. Todos los puntos de la mitad inferior del gráfico Smith tienen reactancias negativas y por lo tanto todos los puntos de coeficiente de reflexión trazados en la mitad inferior del gráfico Smith indican impedancias capacitivas. La línea horizontal a través de la mitad del gráfico de Smith indica resistencia pura así como el círculo unitario indica una reactancia pura.
Una gran diferencia entre la forma menos densa de la tabla de impedancia Smith, Figura\(\PageIndex{6}\) (a), y la gráfica Smith de impedancia completa de la Figura 8-5 es que los signos de las reactancias faltan en el gráfico Smith de impedancia completa. Esto es simplemente porque no hay suficiente espacio y el usuario debe agregar el letrero apropiado al leer el gráfico. Por lo tanto, es esencial que el usuario tenga en cuenta las anotaciones de la Figura\(\PageIndex{6}\) (b). Otro factor más que dificulta el desarrollo de las habilidades esenciales de la gráfica de Smith.
Ejemplo\(\PageIndex{1}\): Impedance Plotting
Trazar las impedancias normalizadas\(z_{A} = 1 − 2\jmath\) y\(z_{B} = 0.3+0.6\jmath\) en una gráfica de impedancia Smith.
Solución
La impedancia\(z_{A} = 1 − 2\jmath\) se representa como Punto\(\mathsf{A}\) a la derecha. Para graficar esto primero identifica el círculo de resistencia normalizada constante\(r = 1\), y luego identificar el arco de reactancia normalizada constante\(x = −2\). La intersección del círculo y el arco se localiza\(z_{A}\) en el punto\(\mathsf{A}\). Se anima al lector a hacer esto con la gráfica Smith de impedancia completa como se muestra en la Figura\(\PageIndex{5}\). Recordemos que faltan señales de reactancias en el gráfico completo. Como ejercicio se lee el coeficiente de reflexión (la respuesta es\(0.5−\jmath 0.5=0.707\angle −45^{\circ}\)).
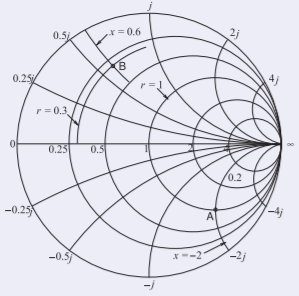
Figura\(\PageIndex{4}\)
La impedancia\(z_{B} = 0.3 + 0.6\jmath\) se traza como Punto\(\mathsf{B}\) que se encuentra en la intersección del círculo\(r = 0.3\) y el\(\text{arc} x = +0.6\). Se requiere interpolación para identificar el círculo y el arco requeridos. El lector debe hacer esto con la tabla Smith de impedancia completa. Como ejercicio se lee el coeficiente de reflexión (la respuesta es\(−0.268 + \jmath 0.585 = 0.644\angle 115^{\circ}\)).
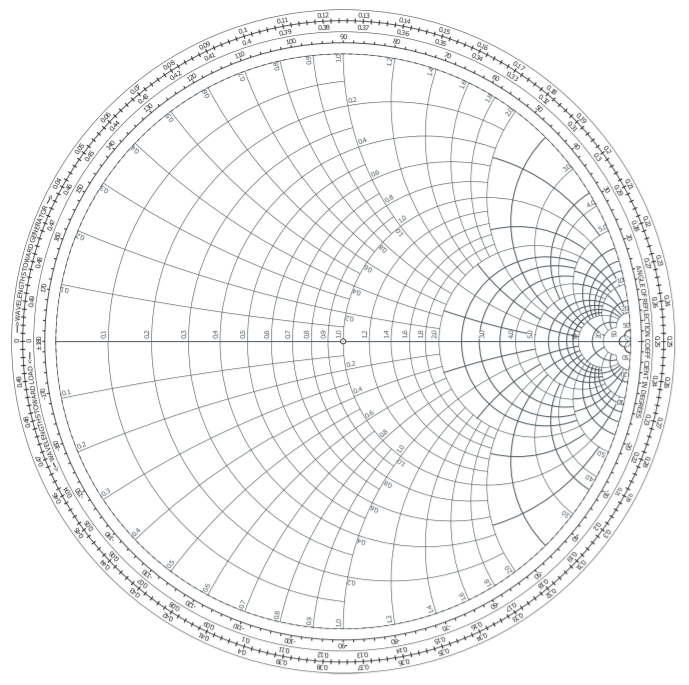
Figura\(\PageIndex{5}\): Gráfica de Impedancia Smith. También se llama gráfico Smith normalizado ya que las resistencias y reactancias se han normalizado a la impedancia de referencia del sistema\(Z_{\text{REF}}: z = Z/Z_{\text{REF}}\). Un punto trazado en el gráfico de Smith representa un número complejo\(A\). La magnitud de\(A\) se obtiene midiendo la distancia desde el origen de la gráfica polar (la misma que el origen de la gráfica Smith en el centro del círculo unitario) hasta apuntar\(A\), digamos usando una regla, y comparándola con la medición del radio del círculo unitario que corresponde a una número complejo con una magnitud de\(1\). El ángulo en grados del número complejo\(A\) se lee desde la escala circular más interna. La técnica utilizada es dibujar una línea recta desde el origen a través del punto\(A\) hacia fuera hasta la escala circular.
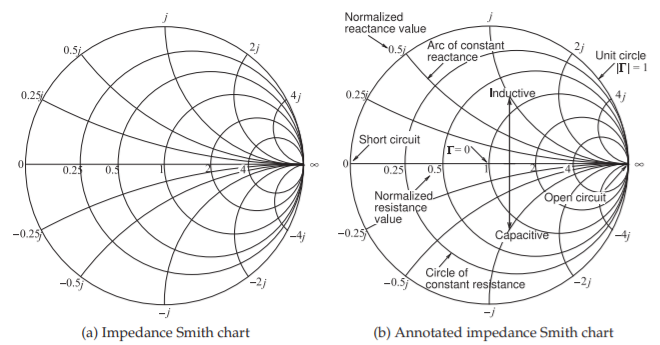
Figura\(\PageIndex{6}\): Gráficas Smith de impedancia normalizada.
Ejemplo\(\PageIndex{2}\): Impedance Synthesis
Utilice una longitud de línea de transmisión terminada para realizar una impedancia de\(Z_{\text{in}} = \jmath 140\:\Omega\).
Solución
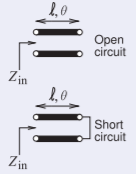
Figura\(\PageIndex{7}\)
La impedancia a sintetizar es reactiva por lo que la terminación también debe ser sin pérdidas. La terminación más simple es un cortocircuito o un circuito abierto. Ambos casos serán considerados. Elija una línea de transmisión con una impedancia característica,\(Z_{0}\), de\(100\:\Omega\) manera que la impedancia de entrada normalizada deseada sea\(\jmath 140\:\Omega /Z_{0} = 1.4\jmath\), trazada como punto\(\mathsf{B}\) en la Figura\(\PageIndex{8}\).
Primero, el caso de cortocircuito. En Figura\(\PageIndex{8}\), considere el camino\(\mathsf{AB}\). La terminación es un cortocircuito y la impedancia de esta carga es Punto\(\mathsf{A}\) con una longitud de referencia de\(\ell_{A} = 0\lambda\) (desde la escala circular más externa). El ángulo de referencia del coeficiente de reflexión correspondiente a la escala es\(θ_{A} = 180^{\circ}\) (desde la escala circular más interna etiquetada como 'ENGENTURAS DE ONDA HACIA EL GENERADOR' que es lo mismo que 'longitudes de onda alejadas de la carga'). A medida que aumenta la longitud de la línea, la impedancia de entrada de la línea terminada sigue la trayectoria en sentido horario hasta el punto\(\mathsf{B}\) donde está la impedancia de entrada normalizada\(\jmath 1.4\). (Para verificar su comprensión de que el lugar geométrico del coeficiente de refección gira en el sentido de las agujas del reloj, es decir, ángulo cada vez más negativo a medida que aumenta la longitud de la línea, consulte la Sección 3.3.3 En Punto\(\mathsf{B}\) la longitud de la línea de referencia\(\ell_{B} = 0.1515\lambda\) y el ángulo de referencia del coeficiente de reflexión correspondiente de la escala es\(θ_{B} = 71.2^{\circ}\). El ángulo del coeficiente de reflexión y la longitud en términos de longitudes de onda se leyeron directamente de la tabla de Smith y se debe tener cuidado de que se use el signo correcto y la escala correcta. Una buena estrategia es correlacionar las escalas con las propiedades fácilmente recordadas en los puntos de circuito abierto y cortocircuito. Aquí la longitud de la línea es
\[\label{eq:3}\ell =\ell_{B}-\ell_{A}=0.1515\lambda -0\lambda =0.1515\lambda \]
y la longitud eléctrica es la mitad de la diferencia en los ángulos del coeficiente de reflexión,
\[\label{eq:4}\theta =\frac{1}{2}|\theta_{B}-\theta_{A}|=\frac{1}{2}|71.2^{\circ}-180^{\circ}|=54.4^{\circ} \]
correspondiente a una longitud de\((54.4^{\circ}/360^{\circ})\lambda = 0.1511\lambda\) (la discrepancia con la longitud de línea previamente determinada de\(0.1515\lambda\) es pequeña). Esto es lo más cercano que podría esperarse al usar las escalas. Por lo que la longitud del trozo con una terminación de cortocircuito es\(0.1515\lambda\).
Para el trozo de circuito abierto, la trayectoria comienza en el punto de impedancia infinita\(\Gamma = +1\) y gira en sentido horario a Punto\(\mathsf{A}\) (esto es a\(90^{\circ}\) o\(0.25\lambda\) rotación) antes de continuar hacia Punto\(\mathsf{B}\). Para el trozo de circuito abierto,
\[\label{eq:5}\ell =0.1515\lambda +0.25\lambda =0.4015\lambda \]
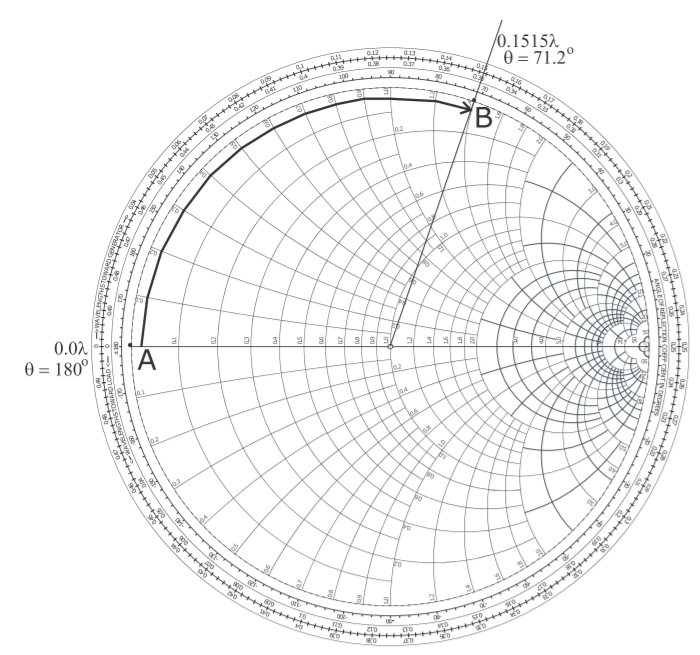
Figura\(\PageIndex{8}\): Diseño de un trozo de cortocircuito con una impedancia de entrada normalizada de\(\jmath 1.4\). El camino\(\mathsf{AB}\) está en realidad en el círculo unitario pero se ha desplazado aquí para evitar cubrir números. La longitud eléctrica en longitudes de onda se ha leído desde la escala circular más externa, y el ángulo, en grados\(\Theta\), se refiere al ángulo de la gráfica polar (y es el doble de la longitud eléctrica).
8.3.2 Gráfico de admisiones Smith
La gráfica Smith de admitancia tiene loci para susceptancias constantes discretas que van desde\(−∞\) hasta\(∞\), y para conductancia constante discreta que van desde\(0\) hasta\(∞\), ver Figura\(\PageIndex{9}\). Una forma menos densa se muestra en la Figura\(\PageIndex{10}\) (a). Este gráfico se parece a la versión invertida del gráfico Smith de impedancia pero es la misma gráfica polar de un coeficiente de reflexión para que las posiciones del circuito abierto y cortocircuito sigan siendo las mismas que lo hacen las mitades capacitiva e inductiva del gráfico Smith. En la versión completa de la tabla de admisiones Smith, Figura\(\PageIndex{9}\), se han dejado caer señales ya que no hay lugar para ellas. Por lo tanto, interpretar las admisiones del gráfico requiere que el usuario determine por separado los signos de susceptancias. La versión menos densa, Figura\(\PageIndex{10}\) (a),
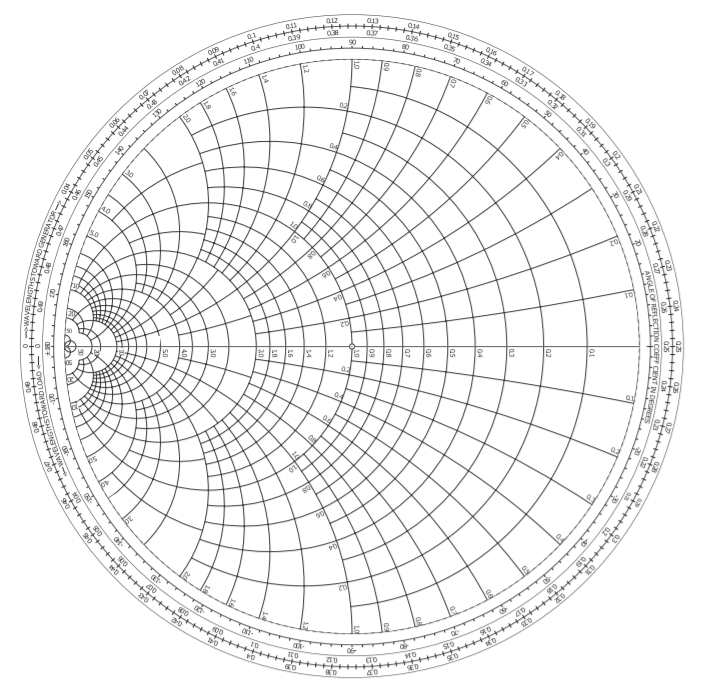
Figura\(\PageIndex{9}\): Gráfico de admisiones Smith.
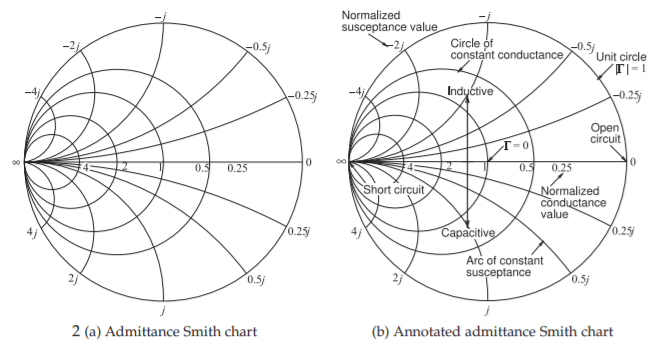
Figura\(\PageIndex{10}\): Gráfica Smith de admisión normalizada.
conserva las señales facilitando el seguimiento de algunas de las discusiones y ejemplos. Es importante que el usuario entienda fácilmente las anotaciones en la forma menos densa del gráfico Smith, ver Figura\(\PageIndex{10}\) (b).
8.3.3 Gráfico Combinado Smith
La combinación de las gráficas polares de reflexión/transmisión, los nomógrafos y la gráfica Smith de impedancia y admitancia conduce a la gráfica Smith combinada (ver Figura\(\PageIndex{11}\)). Esta carta de color Smith es la versión preferida para su uso en el diseño y las versiones separadas de impedancia y admitancia del gráfico Smith rara vez se utilizan. Los gráficos Smith combinados son ricos en información y se requiere cuidado para identificar las líneas que corresponden a admitancias (específicamente líneas de conductancia normalizada constante y susceptancia normalizada constante), y las líneas que corresponden a impedancias (resistencias normalizadas constantes y constantes reactancias normalizadas). Los signos de las reactancias y susceptibles faltan y se dejan al usuario para agregarlos dependiendo de si un punto de coeficiente de reflexión es capacitivo (en la mitad inferior del gráfico Smith y por lo tanto las susceptancias son positivas y las reactancias son negativas) o si un punto es inductivo (en la mitad superior de la gráfica Smith y por lo tanto las susceptancias son negativas y las reactancias son positivas). En la Figura\(\PageIndex{12}\) (a) se muestra una versión menos densa del gráfico combinado de Smith, con la adición de signos.
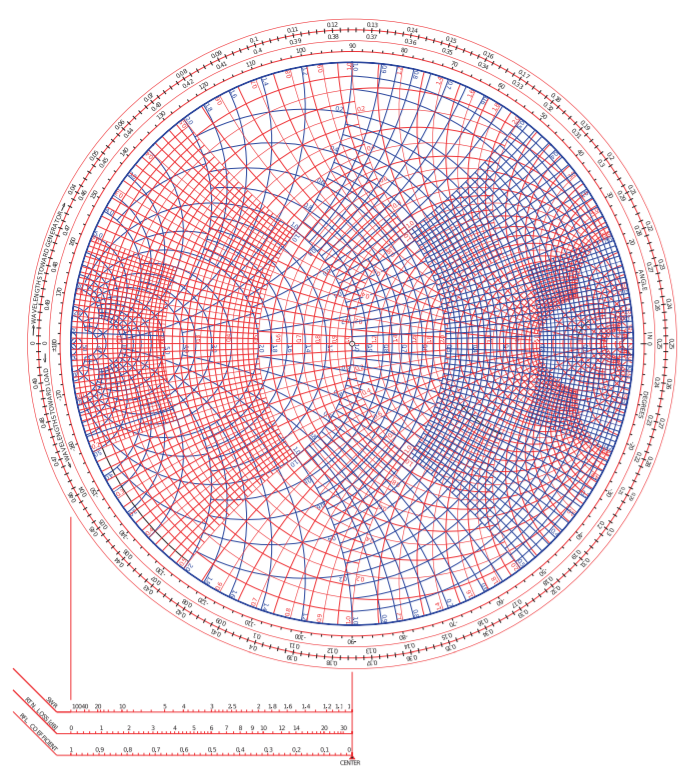
Figura\(\PageIndex{11}\): Gráfica Smith combinada normalizada que combina tablas Smith de impedancia y admisión.
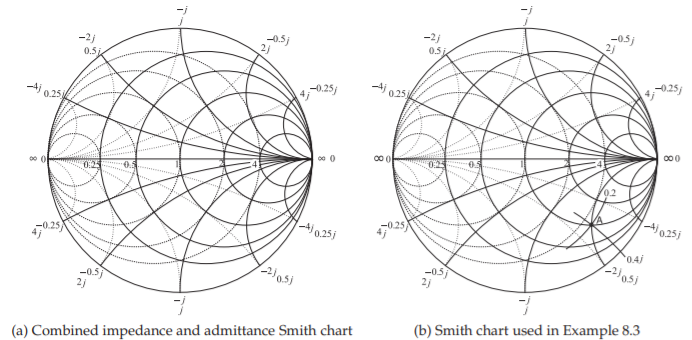
Figura\(\PageIndex{12}\): Gráfico combinado de impedancia y admisión Smith.
Ejemplo\(\PageIndex{3}\): Impedance to Admittance Conversion
Utilice una gráfica de Smith para convertir la impedancia\(z = 1 − 2\jmath\) en una admitancia.
Solución
La impedancia\(z = 1−2\jmath\) se representa como Punto\(\mathsf{A}\) en la Figura\(\PageIndex{12}\) (b). Para leer la admitancia del gráfico, las líneas de conductancia constante y susceptancia constante deben ser interpoladas a partir de los arcos y círculos proporcionados. Las interpolaciones se muestran en la figura, indicando una conductancia de\(0.2\) y una susceptancia de\(0.4\jmath\). Por lo tanto
\[y=0.2+0.4\jmath\nonumber \]
(Esto concuerda con el cálculo:\(y = 1/z = 1/(1 − 2\jmath )=0.2+0.4\jmath\).)
Adición de reactancia y susceptancia
Una buena cantidad de diseño de microondas, como el diseño de una red coincidente para la máxima transferencia de potencia, implica comenzar con una impedancia de carga trazada en un gráfico Smith e insertar reactancias en serie y derivación, y líneas de transmisión, para transformar la impedancia a otro valor. La visión preferida del proceso de diseño es la de un coeficiente de reflexión que evoluciona gradualmente de un valor a otro. Es decir, en el caso de una reactancia en serie, el efecto es el de un coeficiente de reflexión que cambia gradualmente a medida que las reactancias aumentan de cero a su valor real. El camino trazado por el valor del coeficiente de reflexión que evoluciona gradualmente se denomina locus. Los loci de los elementos de circuito comunes añadidos a diversas cargas se muestran en la Figura\(\PageIndex{13}\). Para cada locus la carga se encuentra al inicio de la flecha con el valor del elemento aumentando de cero a su valor final real en la punta de la flecha.
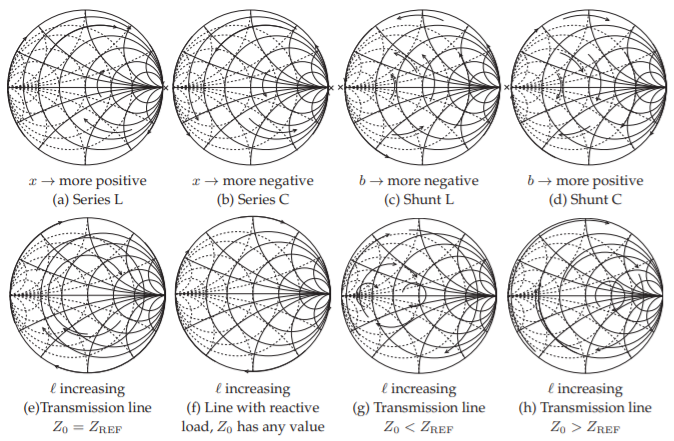
Figura\(\PageIndex{13}\): Loci de coeficiente de reflexión de una carga aumentada por elementos como se indica. La carga original se encuentra al inicio del arco con flecha. En (a) y (b) cada locus es con respecto al incremento\(|x|\) (magnitud de reactancia normalizada), en (c) y (d) el locus es con respecto al incremento\(|b|\) (magnitud de susceptancia normalizada), y en (e) — (h) con respecto al incremento de longitud\(\ell\). En (e) — (h) los loci son partes de círculos centrados en la\(x = 0\) línea. \(\mathsf{x}\)indica que el locus no puede cruzar el infinito (circuito abierto para (a) y (b), cortocircuito para (c) y (d)).
8.3.4 Manipulaciones de la Gráfica Smith
El diseño de microondas a menudo procede tomando una carga conocida y transformándola en otra impedancia, tal vez para una máxima transferencia de potencia. Los gráficos de Smith se utilizan para mostrar estas manipulaciones. En el diseño las manipulaciones requeridas no se conocen por adelantado y la carta Smith permite identificar las requeridas. Excepto en situaciones particulares, se utilizan elementos sin pérdidas como reactancias y líneas de transmisión. Las pocas situaciones en las que se introducen resistencias incluyen introducir estabilidad en osciladores y amplificadores, y reducir deliberadamente los niveles de señales. La mayoría de las veces, la introducción de resistencias aumenta innecesariamente el ruido y reduce los niveles de señal, lo que reduce las relaciones críticas de señal a ruido.
El circuito de la Figura se\(\PageIndex{14}\) utilizará para ilustrar las manipulaciones en una gráfica de Smith. La visión más común es considerar que la gráfica de Smith es una gráfica del coeficiente de reflexión en diversas etapas del circuito, es decir,\(\Gamma_{A},\:\Gamma_{B},\:\Gamma_{C},\:\Gamma_{D},\) y\(\Gamma_{\text{IN}}\). Adicionalmente se traza la carga\(Z_{L}\), y las reactancias, susceptancias o líneas de transmisión transforman el coeficiente de reflexión de una etapa a la siguiente. Otro concepto más es la idea de que se considera que el efecto de un elemento aumenta gradualmente desde un valor insignificante hasta el valor real final y al hacerlo trazar un locus que termina en una punta de flecha. Este es el enfoque que utilizan casi todos los ingenieros de RF y microondas. Las manipulaciones correspondientes al circuito se ilustran en la Figura\(\PageIndex{15}\). Los pasos individuales se identifican en la Figura\(\PageIndex{16}\). Los primeros pasos se limitan a la mitad superior de la tabla de Smith que se repite a mayor escala en la Figura\(\PageIndex{17}\) para los tres primeros pasos.
Paso 1\(\mathsf{L},\text{ a, b, c, d, e, f}\)
El primer paso es trazar la carga\(Z_{L}\) en una gráfica de Smith y este es el Punto\(\mathsf{L}\) en Figuras\(\PageIndex{15}\) —\(\PageIndex{16}\). La impedancia de referencia\(Z_{\text{REF}}\) se elige para que sea\(50\:\Omega\), la misma que la impedancia característica de la línea de transmisión en el circuito. Esta es una elección común porque entonces el locus de variación del coeficiente de reflexión introducido por la línea será un círculo centrado en el origen de la carta de Smith. Para graficar\(\mathsf{L}\) derivar la impedancia de carga normalizada\(z_{L} = Z_{L}/Z_{\text{REF}} = 0.3 +\jmath 0.6\) (los valores numéricos futuros se dan en la Figura\(\PageIndex{14}\)).
Para trazar\(z_{L}\) el círculo de resistencia normalizado para\(0.3\) y el arco de reactancia normalizada para se\(+0.3\) debe ubicar. El círculo de resistencia se identifica a partir de la escala en el eje horizontal de la gráfica Smith, ver el valor circular etiquetado como '\(a\)'. La localización del arco de\(+0.3\) reactancia no es tan directa como faltan los signos de reactancia en el gráfico de Smith. Refiriéndose de nuevo a la Figura,\(\PageIndex{6}\) se observa que una impedancia inductiva está en la mitad superior del gráfico de Smith y por lo tanto las reactancias positivas están en la mitad superior. Así, el arco de\(+0.3\) reactancia se encuentra en la mitad superior del gráfico de Smith y el arco correcto se identifica por '\(c\)'. A partir de las curvas identificadas por\(a\) '' y\(c\) '' los arcos '\(b\)' y\(d\) 'se dibujan con la impedancia\(z_{L}\), es decir\(\mathsf{L}\), punto, en la intersección de los arcos.
Es instructivo determinar\(\Gamma_{L}\), el coeficiente de reflexión a\(\mathsf{L}\). En el gráfico Smith\(\Gamma_{L}\) se dibuja el vector del coeficiente de reflexión desde el origen hasta el punto\(\mathsf{L}\). \(\Gamma_{L}\)se evalúa determinando por separado su magnitud y ángulo. Para determinar la magnitud, mida la longitud del\(|\Gamma_{L}|\) vector usando una regla, una brújula o marcando el borde de una hoja de papel. Entonces esta longitud se puede comparar con la escala del coeficiente de reflexión que se muestra en la parte inferior de la figura\(\PageIndex{15}\) rindiendo\(|\Gamma_{L}| = 0.644\). Alternativamente, la distancia desde el origen hasta el círculo unitario se puede medir usando una regla y la relación de la\(|\Gamma_{L}|\) medición y de la medida del círculo unitario tomado como el valor de\(|\Gamma_{L}|\). El ángulo de\(\Gamma_{L}\) se lee extendiendo el\(\Gamma_{L}\) vector hacia fuera a la escala más circular interna en el gráfico de Smith. Esta extensión está etiquetada como e. El ángulo es
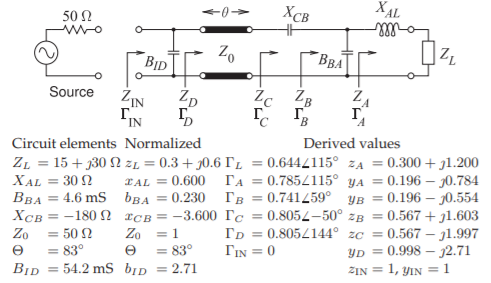
Figura\(\PageIndex{14}\): Circuito utilizado para ilustrar las manipulaciones de la gráfica Smith. \(Z_{\text{REF}} = 50\:\Omega,\: Y_{\text{REF}} = 1/Z_{\text{REF}} = 20\text{ mS},\: z = Z/Z_{\text{REF}},\: y = Y/Y_{\text{REF}},\: Z_{\text{IN}} = Z_{\text{REF}} = 50\:\Omega\). En el circuito\(B\) indica susceptancia e\(X\) indica reacción.
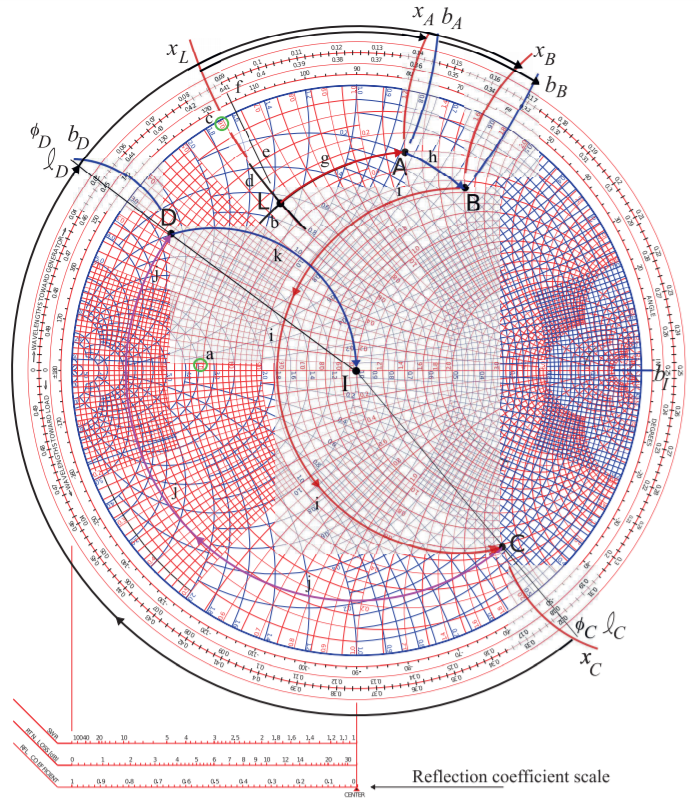
Figura\(\PageIndex{15}\): Smith grafica manipulaciones correspondientes al circuito de la Figura\(\PageIndex{14}\) con elementos de circuito agregados uno a la vez comenzando con la impedancia de carga en Punto\(\mathsf{L}\).
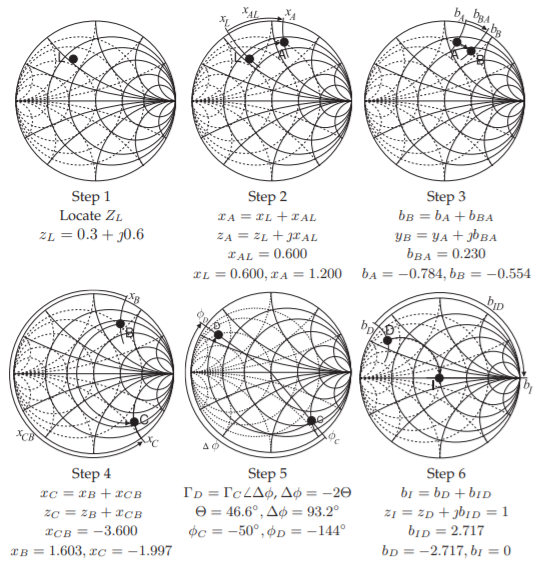
Figura\(\PageIndex{16}\): Pasos en las manipulaciones de la gráfica Smith mostradas en las Figuras\(\PageIndex{15}\) y\(\PageIndex{17}\).
leer en el punto 'f' como\(115^{\circ}\). Por lo tanto\(\Gamma_{L} = 0.644\angle 115^{\circ}\).
Paso 2 Agregue la reactancia en serie\(X_{AL}\), ruta\(\mathsf{L}\) a\(\mathsf{A}\),\(\mathsf{g}\)
En la etapa 2 un inductor con reactancia\(X_{AL}\) está en serie con\(Z_{L}\) y el coeficiente de reflexión transita de punto\(\mathsf{L}\) a punto\(\mathsf{A}\). Ahora\(x_{L} = ℑ\left\{z_{L}\right\} = 0.6\). A esto\(x_{AL} = 0.6\) se le suma para que la reactancia normalizada a\(A\) sea\(x_{A} = x_{L} + x_{AL} = 0.6+0.6=1.2\). El locus de esta operación es el arco, 'g', que se extiende desde\(\mathsf{L}\) la reactancia en serie gradualmente creciente hasta que se obtiene el valor completo\(x_{AL}\), en la punta de flecha del locus. El procedimiento consiste en identificar el arco de\(x_{A} = +1.2\) reactancia y luego seguir el círculo de resistencia constante (ya que la resistencia no está cambiando) hasta este arco. Esta operación traza el locus 'g'.
Paso 3 Agregar la susceptancia de derivación\(B_{BA}\), ruta\(\mathsf{A}\) a\(\mathsf{B}\),\(\mathsf{h}\)
En la etapa 3 un condensador con susceptancia\(X_{BA}\) está en derivación con\(Z_{A}\) y el coeficiente de reflexión transita de punto\(\mathsf{A}\) a punto\(\mathsf{B}\). El locus de esta operación sigue un círculo de conductancia constante con solo ellos cambiando la susceptancia. El valor final debe calcularse como\(b_{B} = b_{A} + b_{BA}\). La susceptancia\(b_{B}\) se lee de la gráfica como\(−0.784\). Este valor se lee siguiendo el arco de susceptancia constante hacia el círculo unitario donde\(0.784\) se lee un valor de. Tenga en cuenta que el arco debe ser interpolado y que el usuario debe darse cuenta de que la susceptancia es negativa en la mitad superior del
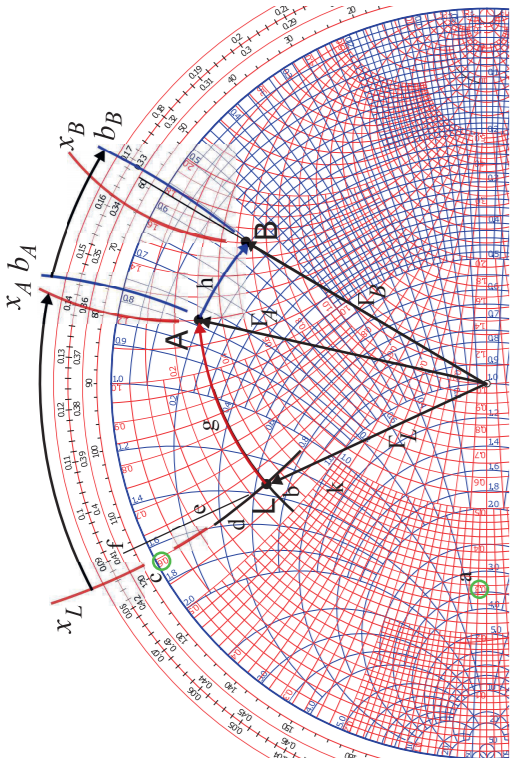
Figura\(\PageIndex{17}\): Los tres primeros pasos en las manipulaciones de la gráfica Smith en la Figura\(\PageIndex{15}\).
Gráfico de Smith por lo que la susceptancia debe ser negativa aunque no se muestre un signo menos en el gráfico de Smith. Así la lectura correcta para\(x_{A}\) es\(−0.784\). Ahora\(b_{BA} = +0.230\) así el locus, 'h', de la transición sigue el círculo de conductancia constante que termina en el (arco interpolado) con susceptancia\(b_{B} = b_{a} + b_{BA} = −0.784 + 0.230 = −0.554\).
Paso 4 Agregue la reactancia en serie\(X_{CB}\), ruta\(\mathsf{B}\) a\(\mathsf{C}\),\(\mathsf{i}\)
En el paso 4 un condensador con reactancia\(X_{CB}\) está en serie con\(Z_{B}\) y el coeficiente de reflexión transita de punto\(\mathsf{B}\) a punto\(\mathsf{C}\). Ahora\(x_{B}\) se lee de la gráfica como\(+1.603\). A esto se suma\(x_{CB} = −3.600\) para que la reactancia normalizada a\(\mathsf{C}\) sea\(x_{C} = x_{B} + x_{CB} = 1.603 + (−3.600) = −1.997\). El locus de\(\mathsf{B}\) a\(\mathsf{C}\), la ruta 'i' comienza en\(\mathsf{B}\) y sigue un círculo de resistencia constante hasta el arco con reactancia normalizada\(x_{C} = −1.997\). Este arco de reactancia se encuentra en la mitad inferior del gráfico de Smith ya que las reactancias son negativas allí a pesar de que faltan señales en las etiquetas de los arcos de reactancia en la mitad inferior del gráfico. El locus de esta operación es el arco, 'g', desde\(\mathsf{L}\) con reactancia en serie gradualmente creciente hasta que se obtiene el valor completo\(z_{CB}\), en la punta de flecha del locus. El procedimiento consiste en identificar el arco de\(x_{C} = −1.997\) reactancia y luego seguir el círculo de resistencia constante (ya que la resistencia no está cambiando) hasta este arco. Esta operación rastrea el locus 'i'.
Paso 5 Inserte la línea de transmisión, camino\(\mathsf{C}\) a\(\mathsf{D}\),\(\mathsf{j}\)
La etapa 5 ilustra un tipo diferente de manipulación ya que ahora hay una línea de transmisión y el coeficiente de reflexión pasa de\(\Gamma_{C}\), es decir, punto\(\mathsf{C}\) al coeficiente de reflexión de entrada de la línea\(\Gamma_{D}\). El lugar geométrico de esta transición debe ser en sentido horario, es decir, tener un ángulo cada vez más negativo (como se discute en la Sección 3.3.3 de [5]). La longitud eléctrica de la línea de transmisión es\(\Theta = 83^{\circ}\) y el coeficiente de reflexión cambia por el negativo del doble de esta cantidad,\(\phi_{DC} = −2\Theta = −166^{\circ}\). El locus se dibuja en la Figura\(\PageIndex{15}\) con la línea de transmisión aumentando gradualmente en longitud trazando un círculo que\(Z_{0} = Z_{\text{REF}}\), ya que, se centra en el origen del carro Smith. El procedimiento consiste en encontrar el valor de escala del ángulo en el punto\(\mathsf{C}\) que se lee dibujando una línea desde el origen a través de la\(\mathsf{C}\) intersección de la escala del ángulo del coeficiente de reflexión (la escala circular más interna) cediendo\(\phi_{C} = −50.4^{\circ}\) y así\(\phi_{D} = \phi_{C} +\phi_{DC} = −50.4^{\circ} − 166^{\circ} + 360^{\circ}) = +143.6^{\circ}\). El lugar geométrico de\(\mathsf{C}\) a\(\mathsf{D}\) se dibuja dibujando primero una línea desde el origen hasta el\(\phi_{D} = −143.6^{\circ}\) punto en la escala del ángulo. Entonces el punto\(\mathsf{D}\) estará en la intersección de esta línea y un círculo de radio constante dibujado a través\(\mathsf{C}\). El locus se muestra como ruta 'j' en la Figura\(\PageIndex{15}\).
Paso 6 Agregue la susceptancia de derivación\(B_{ID}\), ruta\(\mathsf{D}\) a\(\mathsf{I}\),\(\mathsf{k}\)
El paso final es agregar el condensador de derivación con susceptancia\(B_{ID}\) a\(Z_{D}\). Siguiendo el procedimiento anterior\(b_{D}\) se lee en cuanto\(−2.71\) a cuál\(b_{ID} = 2.71\) se agrega de manera que esa\(b_{I} = 0\) que es solo la línea horizontal a través de la mitad del gráfico Smith. Esta línea corresponde a reactancia cero y susceptancia cero. El locus, trayectoria 'k', se extiende desde\(\mathsf{D}\) hasta\(\mathsf{I}\) siguiendo el círculo de conductancia constante. El resultado final es ese\(z_{\text{IN}} = 1.00\) y\(Z_{\text{IN}} = z_{\text{IN}}\cdot Z_{0} = 50\:\Omega\).
Resumen
Las manipulaciones del gráfico Smith consideradas aquí modificaron el coeficiente de reflexión de una carga al agregar elementos de derivación y reactivos en serie. El resultado final de las manipulaciones del circuito es que la impedancia de entrada es\(Z_{\text{IN}} = 50\:\Omega\). Si la fuente tiene una impedancia de fuente Thevenin de\(50\:\Omega\) entonces hay una transferencia de potencia máxima al circuito. Dado que todos los elementos en las manipulaciones del circuito son sin pérdidas esto significa que hay una transferencia máxima de potencia desde la fuente a la carga\(Z_{L}\). Por supuesto, se podrían haber utilizado menos manipulaciones de circuitos para lograr este resultado. Tenga en cuenta que no se consideraron las manipulaciones resultantes de agregar resistencias en serie y/o derivaciones. Es raro que esto sea deseado ya que eso simplemente significa que la potencia se absorbe en la resistencia y se agrega ruido adicional al circuito.
Ejemplo\(\PageIndex{4}\): Reflection Coefficient of a Shorted Microstrip Line on a Smith Chart
 Entorno de Diseño Archivo de Proyecto: RFDesign Shorted Microstrip Line Smith.emp
Entorno de Diseño Archivo de Proyecto: RFDesign Shorted Microstrip Line Smith.emp
En la Figura 8.4.1 se muestra una línea de microcinta cortocircuitada sobre un sustrato de alúmina. La línea tiene bajas pérdidas y por lo tanto siempre\(\Gamma\) está cerca de\(1\). La línea de microcinta se diseñó para ser\(50\:\Omega\) y\(\Gamma\) de la línea de baja pérdida se graficó en un gráfico de\(50\:\Omega\) Smith en la Figura 8.4.2 (a). Trazar\(\Gamma\) en una gráfica de\(50\:\Omega\) Smith indica que el coeficiente de reflexión se calculó con respecto a\(50\:\Omega\). A una frecuencia muy baja,\(0.1\text{ GHz}\) es la frecuencia más baja aquí, el locus del coeficiente de reflexión está muy cerca\(\Gamma = −1\), identificando un cortocircuito. A medida que aumenta la longitud eléctrica, en este caso la frecuencia aumenta a medida que se fija la longitud física de la línea, el lugar geométrico del coeficiente de reflexión se mueve en sentido horario, abrazando el círculo del coeficiente de reflexión unitario. A la frecuencia más alta,\(30\text{ GHz}\), el coeficiente de reflexión es menor que\(1\) y el locus comienza a moverse desde el círculo de unidad. Es interesante ver qué pasa con una línea de alta pérdida, y esto se logra cambiando la tangente de pérdida\(\tan \delta\),, del sustrato de\(0.001\) a\(0.1\). El locus del coeficiente de reflexión de la línea de alta pérdida se muestra en la Figura 8.4.2 (b). La pérdida aumenta a medida que aumenta la longitud eléctrica de la línea y el lugar geométrico del coeficiente de reflexión traza una espiral hacia adentro en sentido horario.
8.3.5 Una Tabla de Admisiones Alternativas
El diseño a menudo requiere cambiar entre la admitancia y la impedancia. Por lo que es conveniente usar el gráfico Smith combinado de colores que se muestra en la Figura\(\PageIndex{11}\). Los gráficos monocromáticos fueron una vez los únicos disponibles y se utilizó una gráfica Smith de impedancia para los cálculos basados en la admisión siempre que los coeficientes de reflexión fueran rotados por\(180^{\circ}\). Esta forma del gráfico Smith no se usa ahora y es muy confusa.
8.3.6 Resumen
El gráfico Smith es la más poderosa de las herramientas utilizadas en RF y Diseño de Microondas. El diseño utilizando gráficos de Smith será considerado en otros capítulos pero en esta etapa el lector debe estar totalmente informado con las técnicas descritas en esta sección.


