8.6: Ejercicios
- Page ID
- 81656
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- En la distribución de señales en un sistema de televisión por cable se utiliza un cable\(75\:\Omega\) coaxial, con una pérdida de\(0.1\text{ dB/m}\) at\(1\text{ GHz}\). Si un suscriptor desconecta un televisor del cable para que la impedancia de carga se vea como un circuito abierto, estime la impedancia de entrada del cable en\(1\text{ GHz}\) y\(1\text{ km}\) desde el suscriptor. Se requiere una respuesta dentro\(1\%\). Estima el error de tu respuesta. Indicar la impedancia de entrada en un gráfico Smith, dibujando el lugar geométrico de la impedancia de entrada a medida que la línea se incrementa en longitud de la nada a\(1\text{ km}\). (Considera que el relleno dieléctrico que tiene la línea\(\varepsilon_{r} = 1\).)
- Una carga resistiva tiene un coeficiente de reflexión con una magnitud de\(0.7\). Si una línea de transmisión se coloca en serie con la carga, en una gráfica polar esboza el lugar del coeficiente de reflexión de entrada mirando a la entrada de la línea terminada a medida que la línea aumenta en longitud eléctrica de cero a\(\lambda /2\). Al leer el gráfico de Smith, determinar la impedancia de entrada normalizada de la línea cuando tiene una longitud eléctrica de\(π/2\).
- Una carga compleja tiene un coeficiente de reflexión de\(0.5+\jmath 0.5\). Si una línea de transmisión se coloca en serie con la carga, en una gráfica polar esboza el lugar del coeficiente de reflexión de entrada mirando a la entrada de la línea terminada a medida que la línea aumenta en longitud eléctrica de cero a\(π/2\).
- Una carga resistiva tiene un coeficiente de reflexión de\(−0.5\). Si una línea de transmisión se coloca en serie con la carga, en una gráfica polar esboza el lugar del coeficiente de reflexión de entrada mirando a la entrada de la línea terminada a medida que la línea aumenta en longitud eléctrica de\(0\) a\(3\lambda /8\).
- \(S_{21}\)de un puerto de dos es\(0.5\). Si una línea de transmisión se coloca en serie con el Puerto 1, en una gráfica polar esboza el lugar\(S_{21}\) del puerto de dos aumentos a medida que la longitud eléctrica de la línea aumenta de cero a\(\lambda /2\).
- Una carga tiene una impedancia\(Z = 115 − \jmath 20\:\Omega\).
- ¿Cuál es el coeficiente de reflexión\(\Gamma_{L}\),, de la carga en un sistema de\(50\:\Omega\) referencia?
- Trazar el coeficiente de reflexión en una gráfica polar del coeficiente de reflexión.
- Si una línea de\(50\:\Omega\) transmisión sin pérdidas de longitud de onda de un octavo de longitud de onda está conectada a la carga, ¿cuál es el coeficiente de reflexión\(\Gamma_{\text{in}}\),, buscando en la línea de transmisión? (Nuevamente, use el sistema de\(50\:\Omega\) referencia.) Trazar\(\Gamma_{\text{in}}\) en la gráfica del coeficiente de reflexión polar de la parte (b). Identificar claramente\(\Gamma_{\text{in}}\) y\(\Gamma_{L}\) en la parcela.
- En el gráfico de Smith, identificar el locus de a\(\Gamma_{\text{in}}\) medida que la longitud de la línea de transmisión aumenta de\(0\) a\(\lambda /8\) largo. Es decir, en el gráfico de Smith, trazar a\(\Gamma_{\text{in}}\) medida que varía la longitud de la línea de transmisión.
- Una carga tiene un coeficiente de reflexión con una magnitud de\(0.5\). Si una línea de transmisión se coloca en serie con la carga, en una gráfica polar esboza el lugar del coeficiente de reflexión de entrada mirando a la entrada de la línea terminada a medida que la línea aumenta en longitud eléctrica de cero a\(\lambda /2\). ¿Cuál es la impedancia de entrada normalizada de la línea cuando tiene una longitud eléctrica de\(\lambda /2\)?
- Una carga resistiva tiene un coeficiente de reflexión con una magnitud de\(0.7\). Si una línea de transmisión se coloca en serie con la carga, en una gráfica polar esboza el lugar del coeficiente de reflexión de entrada mirando a la entrada de la línea terminada a medida que la línea aumenta en longitud eléctrica de cero a\(\lambda /4\). Al leer el gráfico de Smith, determinar la impedancia de entrada normalizada de la línea cuando tiene una longitud eléctrica de\(\lambda /4\).
Los problemas 9—15 se refieren al gráfico Smith normalizado en la Figura\(\PageIndex{2}\) con impedancia de referencia\(Z_{\text{REF}} = 50\:\Omega\) y coeficiente de reflexión\(\Gamma\), coeficiente de reflexión de voltaje\(^{V}\Gamma\)\(^{I}\Gamma\), coeficiente de reflexión de corriente e impedancia\(z = r+\jmath x\) y admitancia normalizadas \(y = g + \jmath b\). \(\Gamma\)se debe dar en formato de ángulo de magnitud. -
- ¿Qué está\(^{V}\Gamma\) en\(\mathsf{A}\)?
- ¿Qué está\(^{I}\Gamma\) en\(\mathsf{A}\)?
- ¿Qué está\(r\) en\(\mathsf{B}\)?
- ¿Qué está\(z\) en\(\mathsf{C}\)?
- ¿Qué está\(y\) en\(\mathsf{D}\)?
- ¿Qué está\(|\Gamma |\) en\(\mathsf{F}\)?
- ¿Qué está\(b\) en\(\mathsf{I}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{P}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{D}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{T}\)?
-
- ¿Qué está\(z\) en\(\mathsf{A}\)?
- ¿Qué está\(y\) en\(\mathsf{I}\)?
- ¿Qué está\(z\) en\(\mathsf{E}\)?
- ¿Qué está\(y\) en\(\mathsf{Z}\)?
- ¿Qué está\(y\) en\(\mathsf{H}\)?
- ¿Qué está\(|\Gamma |\) en\(\mathsf{W}\)?
- ¿Qué está\(b\) en\(\mathsf{F}\)?
- ¿Qué está\(x\) en\(\mathsf{K}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{K}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{R}\)?
-
- ¿Qué está\(y\) en\(\mathsf{A}\)?
- ¿Qué está\(y\) en\(\mathsf{I}\)?
- ¿Qué está\(z\) en\(\mathsf{G}\)?
- ¿Qué está\(y\) en\(\mathsf{O}\)?
- ¿Qué está\(y\) en\(\mathsf{V}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{B}\)?
- ¿Qué está\(x\) en\(\mathsf{C}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{G}\)?
- ¿Qué hay\(z\) en\(\mathsf{L}\), etiquetar esto\(z_{L}\)?
- Utilice el gráfico Smith para encontrar\(z_{\text{in}}\) de una línea\(50\:\Omega\lambda /8\) -larga con carga\(z_{L}\)?
-
- ¿Qué está\(^{V}\Gamma\) en\(\mathsf{M}\)?
- ¿Qué está\(^{I}\Gamma\) en\(\mathsf{M}\)?
- ¿Qué está\(r\) en\(\mathsf{W}\)?
- ¿Qué está\(z\) en\(\mathsf{Y}\)?
- ¿Qué está\(y\) en\(\mathsf{V}\)?
- ¿Qué está\(|\Gamma |\) en\(\mathsf{B}\)?
- ¿Qué está\(b\) en\(\mathsf{K}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{V}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{P}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{N}\)?
-
- ¿Qué está\(z\) en\(\mathsf{M}\)?
- ¿Qué está\(y\) en\(\mathsf{K}\)?
- ¿Qué está\(z\) en\(\mathsf{S}\)?
- ¿Qué está\(y\) en\(\mathsf{R}\)?
- ¿Qué está\(g\) en\(\mathsf{B}\)?
- ¿Qué está\(|\Gamma |\) en\(\mathsf{F}\)?
- ¿Qué está\(b\) en\(\mathsf{B}\)?
- ¿Qué está\(x\) en\(\mathsf{I}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{I}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{Q}\)?
-
- ¿Qué está\(g\) en\(\mathsf{M}\)?
- ¿Qué está\(r\) en\(\mathsf{K}\)?
- ¿Qué está\(y\) en\(\mathsf{S}\)?
- ¿Qué está\(z\) en\(\mathsf{R}\)?
- ¿Qué está\(y\) en\(\mathsf{Z}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{W}\)?
- ¿Qué está\(x\) en\(\mathsf{Y}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{T}\)?
- ¿Qué hay\(z\) en\(\mathsf{O}\), etiquetar esto\(z_{O}\)?
- Usando el hallazgo gráfico Smith\(z_{\text{in}}\) de una\(3\lambda /8\)\(50\:\Omega\) línea larga con carga\(z_{O}\)?
-
- ¿Qué está\(g\) en\(\mathsf{P}\)?
- ¿Qué está\(y\) en\(\mathsf{J}\)?
- ¿Qué está\(\Gamma\) en\(\mathsf{L}\)?
- ¿Qué está\(z\) en\(\mathsf{N}\)?
- ¿Qué está\(y\) en\(\mathsf{S}\)?
- ¿Qué está\(|\Gamma |\) en\(\mathsf{U}\)?
- ¿Qué está\(^{V}\Gamma\) en\(\mathsf{X}\)?
- ¿Qué está\(^{I}\Gamma\) en\(\mathsf{X}\)?
- ¿Qué está\(g\) en\(\mathsf{B}\)?
- ¿Qué está\(x\) en\(\mathsf{I}\)?
- 16. Diseñe un trozo cortocircuitado para realizar una susceptancia normalizada de\(2.15\). Mostrar el locus del trozo a medida que su longitud aumenta de cero a su longitud final. ¿Cuál es la longitud mínima del trozo en términos de longitudes de onda?
- Diseñe un trozo cortocircuitado para realizar una susceptancia normalizada de\(−0.56\). Mostrar el locus del trozo a medida que su longitud aumenta de cero a su longitud final. ¿Cuál es la longitud mínima del trozo en términos de longitudes de onda?
- Diseñe un trozo cortocircuitado para realizar una susceptancia normalizada de\(−2.2\). Mostrar el locus del trozo a medida que su longitud aumenta de cero a su longitud final. ¿Cuál es la longitud mínima del trozo en términos de longitudes de onda?
- Una línea\(75\:\Omega\) de transmisión se termina en una carga con un coeficiente de reflexión,\(\Gamma\), normalizado a\(75\:\Omega\), de\(0.5\angle 45^{\circ}\). Si\(\Gamma\) en la entrada de la línea está\(0.5\angle −135^{\circ}\), cuál es la longitud eléctrica mínima de la línea en grados.
- Una línea de\(75\:\Omega\) transmisión de circuito abierto tiene un coeficiente de reflexión de entrada con un ángulo de\(40^{\circ}\) ¿cuál es la longitud eléctrica de la línea en grados? Si hay más de una respuesta, proporcione al menos dos respuestas correctas.
- Repita el Ejemplo 8.3.1 usando la tabla Smith de impedancia completa de la Figura\(\PageIndex{5}\).
- Trazar las impedancias normalizadas\(z_{A} = 0.5+\jmath 0.5,\: z_{A} = 0.5 +\jmath 0.5,\) y\(z_{B} = 0.185 −\jmath 1.05\) en el gráfico Smith de impedancia completa de la Figura\(\PageIndex{5}\). [Ejemplo de Parallels 8.3.1]
- Una línea de transmisión\(50\:\Omega\) con pérdidas está cortocircuitada en un extremo. La pérdida de línea es\(2\text{ dB}\) por longitud de onda. Tenga en cuenta que dado que la línea tiene pérdidas la impedancia característica será compleja, pero cercana a\(50\:\Omega\), ya que solo es ligeramente con pérdidas. No hay forma de calcular la impedancia característica real con la información proporcionada. Es decir, los problemas deben resolverse con pequeñas inconsistencias. Los ingenieros de microondas hacen lo mejor que pueden en el diseño y siempre confían en las mediciones para calibrar los resultados.
- ¿Cuál es el coeficiente de reflexión a la carga (en este caso el corto)?
- Considere el coeficiente de reflexión de entrada\(\Gamma_{\text{in}}\),, a una\(\ell\) distancia de la carga. Determinar\(\Gamma_{\text{in}}\) para\(\ell\) pasar de\(0.1\lambda\) a\(\lambda\) en pasos de\(0.1\lambda\).
- En una gráfica de Smith grafica el locus de\(\Gamma_{\text{in}}\) de\(\ell = 0\) a\(\lambda\).
- Calcular la impedancia de entrada\(Z_{\text{in}}\),, cuando la línea es\(3\lambda /8\) larga usando la ecuación del telégrafo.
- Repita la parte (d) usando una gráfica de Smith.
- En\(\PageIndex{1}\) la Figura se trazan los resultados de varios experimentos diferentes en una gráfica de Smith. Cada experimento midió el coeficiente de reflexión de entrada de una baja frecuencia (denotada por un círculo) a una frecuencia alta (denotada por un cuadrado) de un puerto. Determinar la carga que se midió. Las cargas que se midieron son una de las que se muestran a continuación.
Tabla\(\PageIndex{1}\)Cargar Descripción i Un inductor ii Un condensador iii Una carga reactiva al final de una línea de transmisión iv Una carga resistiva al final de una línea de transmisión v Una conexión en paralelo de un inductor, una resistencia y un condensador que pasa por resonancia y con un desplazamiento de línea de transmisión vi Una conexión en serie de una resistencia, un inductor y un condensador pasando por resonancia y con un desplazamiento de línea de transmisión vii Resistor e inductor en serie A viii Una carga desconocida y no una de las anteriores
Para cada una de las mediciones a continuación indicamos la carga o cargas utilizando el identificador de carga anterior (e.g., i, ii, etc.).- ¿Qué carga (s) se indica por curva\(\mathsf{A}\)?
- ¿Qué carga (s) se indica por curva\(\mathsf{B}\)?
- ¿Qué carga (s) se indica por curva\(\mathsf{C}\)?
- ¿Qué carga (s) se indica por curva\(\mathsf{D}\)?
- ¿Qué carga (s) se indica por curva\(\mathsf{E}\)?
- ¿Qué carga (s) se indica por curva\(\mathsf{F}\)?
- Diseñe un trozo de circuito abierto con una impedancia de entrada de\(+\jmath 75\:\Omega\). Utilice una línea de transmisión con una impedancia característica de\(75\:\Omega\). [Ejemplo de Parallels 8.3.2]
- Diseñe un trozo cortocircuitado con una impedancia de entrada de\(−\jmath 50\:\Omega\). Utilice una línea de transmisión con una impedancia característica de\(100\:\Omega\). [Ejemplo de Parallels 8.3.2]
- Una carga tiene una impedancia\(Z_{L} = 25 −\jmath 100\:\Omega\).
- ¿Cuál es el coeficiente de reflexión\(\Gamma_{L}\),, de la carga en un sistema de\(50\:\Omega\) referencia?
- Si una línea de\(50\:\Omega\) transmisión de un cuarto de longitud de onda larga está conectada a la carga, ¿cuál es el coeficiente de reflexión\(\Gamma_{\text{in}}\),, buscando en la línea de transmisión?
- Describir el locus de\(\Gamma_{\text{in}}\), ya que la longitud de la línea de transmisión varía de longitud cero a media longitud de onda larga. Usa un gráfico de Smith para ilustrar tu respuesta.
- Una red consiste en una fuente con una impedancia equivalente a Thevenin de\(50\:\Omega\) accionar primero una reactancia en serie de\(−50\:\Omega\) seguida de una línea de transmisión larga de un octavo de longitud de onda con una impedancia característica de\(40\:\Omega\) y un elemento con una impedancia reactiva de\(\jmath 25\:\Omega\) en derivación con una carga tener una impedancia\(Z_{L} = 25 −\jmath 50\:\Omega\). Este problema debe resolverse gráficamente y no se dará crédito si esto no se hace.
- Dibuja la red.
- En una gráfica de Smith, grafica el locus del coeficiente de reflexión primero para la carga, luego con el elemento en derivación, luego mirando hacia la línea de transmisión, y finalmente el elemento serie. Usa letras para identificar cada punto en el gráfico de Smith. Anote el coeficiente de reflexión en cada punto.
- ¿Cuál es la impedancia que presenta la red a la fuente?
8.6.1 Ejercicios por Sección
\(†\)desafiante
\(§8.3 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23†, 24†, 25†, 26†, 27†, 28†\)
8.6.2 Respuestas a ejercicios seleccionados
- \(\Gamma_{\text{IN}}=10^{-10}\)
- (c) ii y iii
- d)\(8.37-\jmath 49.3\:\Omega\)
- \(0.825\angle -50.9^{\circ}\)
- \(\approx 250-\jmath 41\:\Omega\)
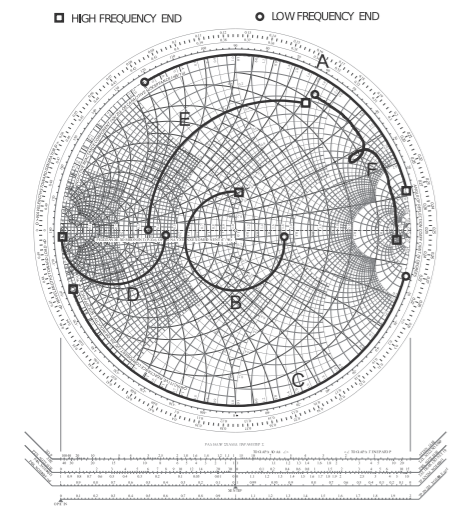
Figura\(\PageIndex{1}\): El lugar geométrico de diversas cargas trazadas en una gráfica de Smith.
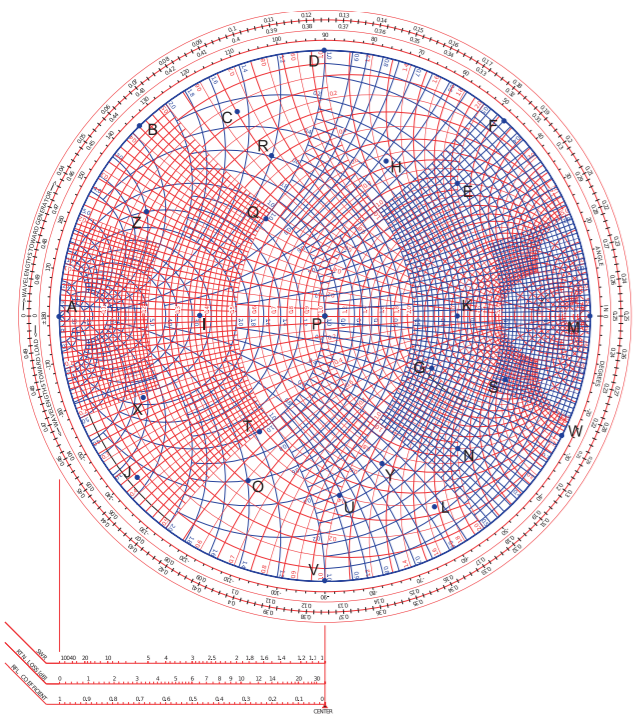
Figura\(\PageIndex{2}\)


