10.6: Manejo de cargas complejas

El ancho de banda de una red coincidente se puede controlar usando múltiples etapas de coincidencia, ya sea haciendo que el ancho de banda coincidente sea más ancho o más estrecho Este concepto se elabora en éste y en varios enfoques de diseño presentados.

10.6.1 Concepto de Diseño para Manipulación de Ancho de Banda

El concepto para manipular el ancho de banda de red coincidente es hacer el emparejamiento en etapas como se muestra en la Figura 10.5.7. La Figura 10.5.7 (a) muestra el problema de emparejamiento de una etapa usando la identificación común de la red coincidente como 'M'. El problema de coincidencia de una etapa se repite en la Figura 10.5.7

Figura\(\PageIndex{1}\): Efecto de la coincidencia multietapa en el circuito\(Q,\: Q_{T}\) total y el ancho de banda coincidente (que es aproximadamente inversamente proporcional a\(Q_{T}\).)

sin mostrar explícitamente el generador de fuentes. Un problema de coincidencia de dos etapas se muestra en la Figura 10.5.7 (c) con la introducción de una resistencia virtual\(R_{V}\) entre la primera\(\text{M}_{1}\), y segunda\(\text{M}_{2}\), redes de adaptación de etapa. \(R_{V}\)se muestra como una conexión virtual ya que en realidad no se inserta en el circuito. En cambio, esta es una manera corta de indicar el problema de coincidencia que se debe hacer en dos etapas como se muestra en la Figura 10.5.7 (d y e) con la primera etapa haciendo coincidir la resistencia\(R_{S}\) de origen\(R_{V}\) y la segunda etapa coincidente con\(R_{V}\) la resistencia de carga\(R_{L}\). Después de que se\(\text{M}_{1}\) haya diseñado la resistencia mirando hacia el puerto derecho de\(\text{M}_{1}\), ver Figura 10.5.7 (d), será\(R_{V}\) así\(R_{V}\) es la resistencia de fuente equivalente a Thevenin\(\text{M}_{2}\). De manera similar, la impedancia de entrada que mira en el puerto izquierdo de\(\text{M}_{2}\) es\(R_{V}\) así\(R_{V}\) es la resistencia de carga efectiva de\(\text{M}_{1}\). Por supuesto estas son las impedancias en la frecuencia central y lejos de la frecuencia central del partido las impedancias de entrada serán complejas.

El concepto detrás del diseño de red coincidente multietapa se muestra en la Figura\(\PageIndex{1}\) donde la coincidencia estándar de una etapa se muestra en la Figura\(\PageIndex{1}\) (a). Si bien esto se muestra para\(R_{L} > R_{S}\) el concepto sostiene para\(R_{L} < R_{S}\). Las flechas siguen el diseño que comienza con la carga y termina en la fuente. Con el partido de una etapa el circuito\(Q\) es fijo y designado aquí como el circuito total\(Q,\: Q_{T}\) siendo el mismo que el\(Q\) de la de una etapa\(R_{L}\) a la red\(R_{S}\) coincidente,\(Q_{SL}\). La coincidencia de dos etapas que reduce el ancho de banda (en comparación con la coincidencia de una etapa) se muestra en la Figura\(\PageIndex{1}\) (b). El total\(Q,\: Q_{T}\), de la segunda etapa es mayor que para el diseño de una etapa porque la relación de\(R_{L}\) a\(R_{V}\) es mayor que la relación de\(R_{V}\) a\(R_{S}\). El ancho de banda también se puede reducir en relación con la coincidencia de una etapa asignando\(R_{V}\) que sea mayor que ambos\(R_{L}\)

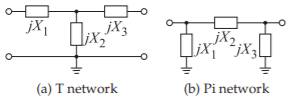
Figura\(\PageIndex{2}\): Dos redes coincidentes de tres elementos.

y\(R_{S}\), ver Figura\(\PageIndex{1}\).

Elegir\(R_{V}\) estar entre\(R_{S}\) y\(R_{L}\) resultará en un circuito con menor\(Q_{T}\) y el ancho de banda del partido aumentará, ver Figura\(\PageIndex{1}\) (d). El ancho de banda máximo para una coincidencia de dos etapas es elegir\(R_{V}\) como la media geométrica de\(R_{S}\) y\(R_{L}\). Este concepto puede extenderse a múltiples etapas como se muestra para un partido de tres etapas en la Figura\(\PageIndex{1}\) (e).

En esta sección se presentan varios diseños de redes coincidentes para manipular el ancho de banda y todos se basan en el concepto de elegir una resistencia virtual.

10.6.2 Redes coincidentes de tres elementos

Con la red L (es decir, coincidencia de dos elementos), el circuito\(Q\) se fija una vez que las resistencias de fuente y carga,\(R_{S}\) y\(R_{L}\), se fijan:

\[\label{eq:1}Q=\sqrt{\frac{R_{L}}{R_{S}}-1},\quad (R_{L}>R_{S}) \]

Así el diseñador no tiene opción de circuito\(Q\). Romper el problema de coincidencia en partes permite\(Q\) controlar el circuito. La introducción de un tercer elemento en la red coincidente proporciona el grado extra de libertad en el diseño para ajustar y\(Q\), por lo tanto, el ancho de banda.

Dos redes coincidentes de tres elementos, la red T y la red Pi, se muestran en la Figura\(\PageIndex{2}\). La red que se utiliza depende de

1. las limitaciones de realización asociadas con el diseño específico, y
2. la naturaleza de las partes reactivas de la fuente y las impedancias de carga y si pueden usarse como parte de la red coincidente.

La red de coincidencia de tres elementos comprende redes coincidentes de\(2\) dos elementos (o L) y se usa para aumentar el ancho de banda general\(Q\) y, por lo tanto, estrecho. Dado\(R_{S}\) y\(R_{L}\), el circuito\(Q\) establecido por una red de coincidencia L es el circuito mínimo\(Q\) disponible en la disposición de emparejamiento de tres elementos. Con la coincidencia de tres elementos, el solo\(Q\) puede aumentar, por lo que la coincidencia de tres elementos se usa para aplicaciones de banda estrecha (alta\(Q\)). Sin embargo, se\(Q\) pueden obtener menores con más de tres elementos. Las siguientes subsecciones consideran emparejar con más de tres elementos.

10.6.3 La Red Pi

La red Pi puede ser pensada como dos redes L back-to-back que se utilizan para hacer coincidir la carga y la fuente con una resistencia virtual,\(R_{V}\), colocadas en el cruce entre las dos redes, como se muestra en la Figura\(\PageIndex{3}\) (b). El diseño de cada sección de la red Pi es como para la correspondencia de la red L. \(R_{S}\)se corresponde con\(R_{V}\) y\(R_{V}\) se corresponde con\(R_{L}\).

\(R_{V}\)debe seleccionarse más pequeño que\(R_{S}\) y\(R_{L}\) ya que está conectado al brazo de serie de cada sección L. Además,\(R_{V}\) puede ser cualquier valor que sea menor que el menor de\(R_{S},\: R_{L}\). Sin embargo, se utiliza habitualmente como parámetro de diseño para especificar el deseado\(Q\).

Figura\(\PageIndex{3}\): Redes de correspondencia Pi: (a) vista de una red Pi; y (b) como dos redes L consecutivas con una resistencia virtual,\(R_{V}\), entre las redes.

Como aproximación de diseño útil, la carga\(Q\) de la red Pi se puede tomar como la\(Q\) de la sección L con la más alta\(Q\):

\[\label{eq:2}Q=\sqrt{\frac{\text{max}(R_{S},\:R_{L})}{R_{V}}-1} \]

Dado\(R_{S},\: R_{L},\) y\(Q\), la ecuación anterior arroja el valor de\(R_{V}\).

Ejemplo\(\PageIndex{1}\): Three-Element Matching Network Design

Diseñe una red Pi para hacer coincidir una\(50\:\Omega\) fuente con una\(500\:\Omega\) carga. Lo deseado\(Q\) es\(10\). Una topología de red adecuada se muestra en la Figura\(\PageIndex{4}\) junto con la resistencia virtual\(R_{V}\), para ser utilizada en el diseño.

Solución

\(R_{S} = 50\:\Omega\)y\(R_{L} = 500\:\Omega\) así\(\text{max}(R_{S}, R_{L}) = 500\:\Omega\) y así la resistencia virtual es

\[\label{eq:3}R_{V}=\frac{\text{max}(R_{S},\:R_{L})}{Q^{2}+1}=\frac{500}{101}=4.95\:\Omega \]

El diseño procede diseñando por separado las redes L a la izquierda y derecha de\(R_{V}\). Para la red L de la izquierda,

\[\label{eq:4}Q_{\text{left}}=\sqrt{\frac{50}{4.95}-1}=3.017\quad\text{so}\quad Q_{\text{left}}=\frac{|X_{a}|}{R_{V}}=\frac{R_{S}}{|X_{1}|}=3.017 \]

Tenga en cuenta que\(X_{1}\) y\(X_{a}\) debe ser de tipos opuestos (uno es capacitivo y el otro es inductivo). La red L izquierda tiene elementos

\[\label{eq:5}|X_{a}|=14.933\:\Omega\quad\text{and}\quad |X_{1}|=16.6\:\Omega \]

Para la red L a la derecha de\(R_{V}\),

\[\label{eq:6}Q_{\text{right}}=Q=10,\quad\text{thus}\quad \frac{|X_{b}|}{R_{V}}=\frac{R_{L}}{X_{3}}=10 \]

\(X_{b},\: X_{3}\)son de tipos opuestos, y

\[\label{eq:7}|X_{b}|=49.5\:\Omega\quad\text{and}\quad |X_{3}|=50\:\Omega \]

La red Pi resultante se muestra en la Figura\(\PageIndex{5}\) con los valores

\[\label{eq:8}|X_{1}|=16.6\:\Omega ,\quad |X_{3}|=50\:\Omega ,\quad |X_{a}|=14.933\:\Omega ,\quad\text{and}\quad |X_{b}|=49.5\:\Omega \]

Tenga en cuenta que el par\(X_{a},\: X_{1}\) es de tipos opuestos y de manera similar\(X_{b},\: X_{3}\) son de tipos opuestos. Por lo que hay cuatro posibles realizaciones, como se muestra en la Figura\(\PageIndex{6}\).

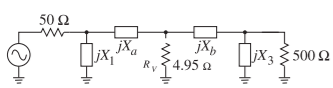
Figura\(\PageIndex{4}\): Problema de red coincidente de Ejemplo\(\PageIndex{1}\).

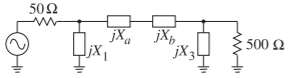
Figura\(\PageIndex{5}\): Red de coincidencia final en Ejemplo\(\PageIndex{1}\).

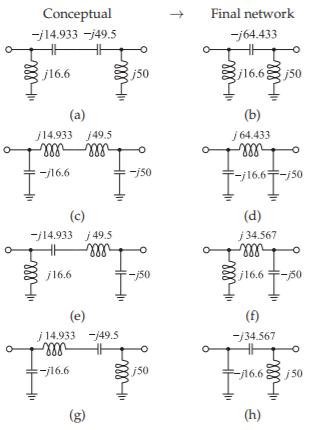
Figura\(\PageIndex{6}\): Cuatro posibles redes de correspondencia Pi: (a), (c), (e) y (g) circuitos conceptuales; y (b), (d), (f) y (h), respectivamente, sus redes Pi reducidas finales.

En el ejemplo anterior hubo cuatro posibles realizaciones de la red coincidente de tres elementos, y esto es cierto en general. La elección específica de una de las cuatro realizaciones posibles dependerá de factores específicos relacionados con la aplicación, como

1. eliminación de reactancias parásitas,
2. la necesidad de pasar o bloquear la corriente CC, y
3. la necesidad de filtrado armónico.

Es una suerte que pueda ser posible lograr múltiples funciones con una misma red.

Ejemplo\(\PageIndex{2}\): Three-Element Matching with Reactive Source and Load

Diseñe una red Pi para que coincida con la fuente con la carga que se muestra. La frecuencia de diseño es\(900\text{ MHz}\) y la deseada\(Q\) es\(10\).

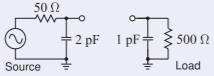
Figura\(\PageIndex{7}\)

Solución

El objetivo del diseño es llegar a una red general que tenga una\(Q\) de\(10\). Para lograr esto es necesario absorber las reactancias de origen y carga en la red coincidente. Si se resonaron en su lugar, se puede esperar que el total\(Q\) de la red sea mayor que el\(Q\) de la red\(L\) coincidente por sí solo.

El diseño comienza considerando la coincidencia de\(R_{S} = 50\:\Omega\) a\(R_{L} = 500\:\Omega\). Dado que\(Q\) se especifica, se deben usar tres (o más) elementos coincidentes. El punto de inicio del diseño se muestra a la derecha:

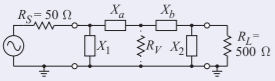
Figura\(\PageIndex{8}\)

La resistencia virtual\(R_{V} = \text{max}(R_{s},\: R_{L})/(1 + Q_{2}) = (500\:\Omega )/(1 + 100) = 4.95\:\Omega\). La subred izquierda con\(X_{1}\) y\(X_{a}\) tiene\(Q_{\text{LEFT}} = \sqrt{R_{S}/R_{V} − 1} = \sqrt{50/4.95 − 1} = 3.017\). La subred correcta con\(X_{2}\) y\(X_{b}\) tiene\(Q_{\text{RIGHT}} = \sqrt{R_{L}/R_{V} − 1} = \sqrt{500/4.95 − 1} = 10.001\).

Nota

Tenga en cuenta que\(Q_{\text{RIGHT}}\) es casi exactamente lo deseado\(Q\) de la red y\(Q_{\text{LEFT}}\) tendrá poco efecto en el\(Q\) del circuito general. Ahora\(Q_{\text{LEFT}} = |X_{a}|/R_{V} = R_{S}/|X_{1}|,\) así\(|X_{a}| = 14.9\:\Omega\) y\(|X_{1}| = 16.57\:\Omega\). \(Q_{\text{RIGHT}} = |X_{b}|/R_{V} = R_{S}/|X_{2}|,\)así\(|X_{b}| = 49.5\:\Omega\) y\(|X_{2}| = 50.0\:\Omega\).

\(X_{1}\)debe elegirse para ser un condensador para\(C_{1} = 10.67\text{ pF}\) que la capacitancia de la\(2\text{ pF}\) fuente pueda ser absorbida. Del mismo modo\(X_{2}\) es un condensador\(C_{2} = 3.53\text{ pF}\). \(X_{a}\)y\(X_{b}\) son ambos inductores que se combinan en serie para una inductancia total\(L_{3} = 11.38\text{ nH}\). Esto lleva al diseño final que se muestra a continuación donde la red coincidente está en la caja discontinua.

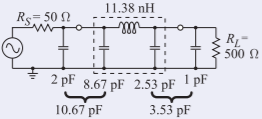
Figura\(\PageIndex{9}\)

10.6.4 Red coincidente\(Q\) revisitada

Para demostrar que el circuito\(Q\) establecido por una red\(L\) coincidente es el circuito mínimo\(Q\) para una red que tiene como máximo tres elementos, considere las ecuaciones de diseño para\(R_{S} > R_{L}\). Refiriéndose a la Figura\(\PageIndex{10}\),

\[\label{eq:9}X_{1}=\frac{R_{S}}{Q},\quad X_{3}=R_{L}\left(\frac{R_{S}/R_{L}}{Q^{2}+1-R_{S}/R_{L}}\right)^{\frac{1}{2}},\quad X_{2}=\frac{QR_{S}+R_{S}R_{L}/X_{3}}{Q^{2}+1} \]

Observe que el denominador de\(X_{3}\) puede escribirse como

\[\label{eq:10}Q^{2}+1-\frac{R_{S}}{R_{L}}=\left(Q+\sqrt{\frac{R_{S}}{R_{L}}-1}\right)\left(Q-\sqrt{\frac{R_{S}}{R_{L}}-1}\right) \]

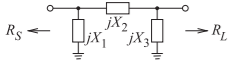
Figura\(\PageIndex{10}\): Una red coincidente de tres elementos.

Figura\(\PageIndex{11}\): Enfoque de diseño de redes T.

Figura\(\PageIndex{12}\): Redes de correspondencia de banda ancha.

Entonces para una solución real debemos tener

\[\label{eq:11}Q\geq\sqrt{\frac{R_{S}}{R_{L}}-1} \]

y así\(Q ≥ Q_{L}\) la red. Para\(Q = Q_{\text{L network}}\),\(X_{3} → ∞\) y la red Pi se reduce a una red L que tiene dos elementos. Por lo tanto, no es posible tener una menor\(Q\) con una red coincidente de tres elementos que la\(Q\) de una red coincidente de dos elementos. Así, una red coincidente de tres elementos debe tener un ancho de banda menor que el de una red coincidente de dos elementos.

10.6.5 La Red T

La red T puede ser pensada como dos redes L back-to-back que se utilizan para hacer coincidir la carga y la fuente con una resistencia virtual,\(R_{V}\), colocadas en el cruce entre las dos redes L (ver Figura\(\PageIndex{11}\)). Se debe seleccionar el RV para que sea mayor que ambos\(R_{S}\) y\(R_{L}\) ya que está conectado a la pata de derivación de cada sección L. \(R_{V}\)se elige de acuerdo con la ecuación

\[\label{eq:12}Q=\sqrt{\frac{R_{V}}{\text{min}(R_{S},\:R_{L})}-1} \]

donde\(Q\) está la carga deseada\(Q\) de la red. Cada red L se calcula exactamente de la misma manera que se hizo para la coincidencia de red Pi. Es decir,\(R_{S}\) se empareja\(R_{V}\) y\(R_{V}\) se empareja con\(R_{L}\). Una vez más habrá cuatro posibles diseños para la red T, dados\(R_{S},\: R_{L},\) y\(Q\).

10.6.6 Coincidencia de banda ancha (baja\(Q\))

L coincidencia de red no permite seleccionar el circuito y\(Q\), por lo tanto, el ancho de banda. Sin embargo, la coincidencia de red Pi y red T permite seleccionar el circuito\(Q\) independientemente de las impedancias de fuente y carga, siempre que la elegida\(Q\) sea mayor que la que se puede obtener con una red L. Así, las redes Pi y T dan como resultado diseños de ancho de banda más estrechos.

Una solución de diseño para la coincidencia de banda ancha es usar dos (o más) secciones L conectadas en serie (ver Figura\(\PageIndex{12}\)). El diseño aún se basa en el concepto de una resistencia virtual,\(R_{V}\), colocada en la unión de las dos redes L (como en la Figura\(\PageIndex{13}\)), pero ahora\(R_{V}\) se elige para estar entre\(R_{S}\) y\(R_{L}\):

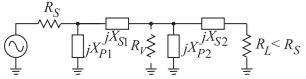
Figura\(\PageIndex{13}\): Red coincidente con dos redes L.

Figura\(\PageIndex{14}\): Redes L en cascada para emparejamiento de banda ancha.

\[\label{eq:13}R_{\text{min}}\leq R_{V}\leq R_{\text{max}} \]

dónde\(R_{\text{min}} = \text{min}(R_{L},\: R_{S})\) y\(R_{\text{max}} = \text{max}(R_{L},\: R_{S})\). Entonces una de las dos redes tendrá

\[\label{eq:14}Q_{1}=\sqrt{\frac{R_{V}}{R_{\text{min}}}-1}\quad\text{and the other}\quad Q_{2}=\sqrt{\frac{R_{\text{max}}}{R_{V}}-1} \]

El ancho de banda máximo (mínimo\(Q\)) disponible se obtiene cuando

\[\label{eq:15}Q_{1}=Q_{2}=\sqrt{\frac{R_{V}}{R_{\text{min}}}-1}=\sqrt{\frac{R_{\text{max}}}{R_{V}}-1} \]

Es decir, el ancho de banda máximo coincidente se obtiene cuando\(R_{V}\) es la media geométrica de\(R_{S}\) y\(R_{L}\):

\[\label{eq:16}R_{V}=\sqrt{R_{L}R_{S}} \]

Incluso se pueden obtener anchos de banda más anchos al conectar en cascada más de dos redes L, como se muestra en la Figura\(\PageIndex{14}\). En este circuito

\[\label{eq:17}R_{S}<R_{V1}<R_{V2}\ldots <R_{Vn-1}<R_{L} \]

Para un ancho de banda óptimo las relaciones deben ser iguales,

\[\label{eq:18}\frac{R_{V_{1}}}{R_{S}}=\frac{R_{V_{2}}}{R_{V_{1}}}=\frac{R_{V_{3}}}{R_{V_{2}}}=\cdots =\frac{R_{L}}{R_{V_{n-1}}} \]

y el\(Q\) es dado por

\[\label{eq:19}Q=\sqrt{\frac{R_{V_{1}}}{R_{S}}-1}=\sqrt{\frac{R_{V_{2}}}{R_{1}}-1}=\cdots =\sqrt{\frac{R_{L}}{R_{V_{n-1}}}-1} \]

Si hay redes\(N\) L utilizadas en el partido, se obtendrá el ancho de banda máximo si la\(i\) resistencia virtual es

\[\label{eq:20}R_{V_{i}}=(R_{S}R_{L})^{i/N},\quad i=1,\ldots ,(N-1) \]

Ejemplo\(\PageIndex{3}\): Two-Section Matching Network Design

Considere hacer coincidir una\(10\:\Omega\) fuente con una\(1000\:\Omega\) carga usando dos redes de coincidencia L y diseñar para una\(Q\) de\(3\). ¿Cuántas secciones coincidentes se requieren?

Solución

Aquí se comparan los\(Q\) aproximados obtenidos con una única red de coincidencia L y con un diseño óptimo de dos secciones. Para un solo diseño de red L

\[\label{eq:21}Q=\sqrt{\frac{R_{L}}{R_{S}}-1}=9.95 \]

Ahora considere un diseño óptimo de dos secciones:

\[\label{eq:22}R_{V}=\sqrt{R_{S}R_{L}};\quad Q_{2}=\sqrt{\frac{R_{L}}{R_{V}}-1}=\sqrt{\sqrt{\frac{R_{L}}{R_{S}}}-1}=3 \]

Así el\(Q\) se\(3\) compara con el\(Q\) de una sección L de\(9.95\). Si el ancho de banda fraccional es inversamente proporcional a\(Q\), entonces el ancho de banda del diseño de dos secciones es\(9.95/3 = 3.32\) veces mayor que el de la sección L.

Ahora considere cuántas secciones se requieren para obtener una\(Q\) de\(2\):

\[\begin{align} \label{eq:23}(1+Q^{2})&=\frac{R_{V_{1}}}{R_{S}}=\frac{R_{V_{2}}}{R_{V_{1}}}=\ldots =\frac{R_{L}}{R_{V_{n-1}}}\Rightarrow \\ \label{eq:24}(1+Q^{2})^{n}&=\frac{R_{L}}{R_{S}}\Rightarrow n\ln (1+Q^{2})=\ln\frac{R_{L}}{R_{S}}\Rightarrow n=\frac{\ln (R_{L}/R_{S})}{\ln (1+Q^{2})}\end{align} \]

Para\(Q = 2\) y\(R_{L}/R_{S} = 100,\: n = 2.86\), a qué rondas\(n = 3\), y se requieren tres secciones.