3.5: Líneas de Transmisión y Gráficos Smith

El locus de una línea de transmisión en un gráfico de Smith es un círculo. Cuando la impedancia característica de la línea es igual a la impedancia de referencia del sistema, este círculo se centra en el origen de la gráfica Smith. El propósito principal de esta sección es considerar la situación en la que la impedancia característica y la impedancia de referencia del sistema difieren.

3.5.1 Transformación bilineal

Matemáticamente, el coeficiente de reflexión de entrada de una línea de transmisión terminada de impedancia característica\(Z_{02}\) se refiere a una impedancia del sistema\(Z_{01}\). Las matemáticas que describen esto se basan en la transformación bilineal. La transformación bilineal generalizada de dos números complejos\(z\) y\(w\) es

\[\label{eq:1}w=\frac{Az+B}{Cz+D} \]

donde\(A,\: B,\: C,\) y\(D\) son constantes\(^{1}\) que a su vez pueden ser complejas. Esto es de interés para tratar con coeficientes de reflexión donde\(w\) y\(z\) son coeficientes de reflexión y\(A,\: B,\: C,\) y\(D\) describen la red de dos puertos conectada a una carga con un coeficiente de reflexión complejo\(z\), y\(w\) es el coeficiente de reflexión que busca la red. La propiedad especial de la transformada bilineal es que un círculo en el plano complejo (aquí el locus de\(z\)) se mapee en otro círculo (aquí el locus de\(w\)) en el plano complejo. (Esto se muestra en la Sección 1.A.14 de [11].)

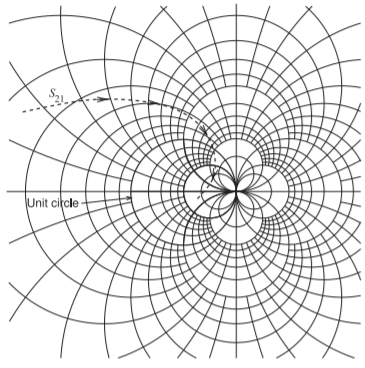
Figura\(\PageIndex{1}\): Gráfica Smith expandida utilizada para trazar parámetros de dispersión con una magnitud mayor que\(1\). El parámetro de transmisión directa\(S_{21}\),, de un transistor se muestra con las flechas en la dirección de frecuencia creciente. Se muestra el círculo unitario de una gráfica Smith convencional.

3.5.2 Cambio de impedancia de referencia como transformada bilineal

En la Figura\(\PageIndex{2}\) una carga fija termina una línea de transmisión de impedancia característica\(Z_{01}\) y el coeficiente de reflexión de entrada es\(\Gamma_{\text{in}}\). Como se mostrará, el locus de\(\Gamma_{\text{in}}\), normalizado a cualquier impedancia del sistema, es un círculo en el plano complejo a medida que aumenta la longitud eléctrica de la línea. La longitud eléctrica de la línea aumenta a medida que aumenta la frecuencia con la longitud física de la línea mantenida constante, o cuando la longitud física de la línea aumenta con la frecuencia mantenida constante.

De la Ecuación ((2.3.4)) de [11] el coeficiente de reflexión de una carga a la que\(Z_{L}\) se hace referencia\(Z_{01}\) es

\[\label{eq:2}\Gamma_{L, Z01}=\frac{Z_{L}-Z_{01}}{Z_{L}+Z_{01}} \]

y el coeficiente de reflexión de entrada al que se hace referencia\(Z_{01}\) es

\[\label{eq:3}\Gamma_{\text{in }, Z01}=\Gamma_{L, Z01}\text{e}^{-\jmath 2\theta} \]

donde\(\theta = \beta\ell\) está la longitud eléctrica de la línea. A\(\theta\) medida que aumenta desde cero,\(\Gamma_{\text{in, }Z01}\) trazado en un gráfico polar traza un círculo que gira en el sentido de las agujas del reloj. El resultado importante que se desarrollará en esta sección es que cuando el coeficiente de reflexión de entrada se hace referencia a otra impedancia, el nuevo coeficiente de reflexión también trazará un círculo. El desarrollo de\(\Gamma_{\text{in, }Z02}\) (el coeficiente de reflexión de entrada al que se hace referencia\(Z_{02}\)) comienza calculando la impedancia de entrada de la línea (en la Figura\(\PageIndex{2}\)):

\[\label{eq:4}Z_{\text{in}}=Z_{01}\frac{1+\Gamma_{\text{in, }Z01}}{1-\Gamma_{\text{in },Z01}} \]

de manera que el coeficiente de reflexión al que se hace referencia\(Z_{02}\) es

\[\begin{align}\Gamma_{\text{in, }Z02}&=\frac{Z_{\text{in}}-Z_{02}}{Z_{\text{in}}+Z_{02}}=\frac{(Z_{\text{in}}-Z_{02})(1-\Gamma_{\text{in, }Z01})}{(Z_{\text{in}}+Z_{02})(1-\Gamma_{\text{in, }Z01})} \nonumber \\ &=\frac{(Z_{01}+Z_{02})\Gamma_{\text{in, }Z01}+(Z_{01}-Z_{02})}{(Z_{01}-Z_{02})\Gamma_{\text{in, }Z01}+(Z_{01}+Z_{02})} \nonumber \\ \label{eq:5}&=\frac{\Gamma_{\text{in, }Z01}+B}{B\Gamma_{\text{in, }Z01}+1}=\frac{A\Gamma_{\text{in, }Z01}+B}{C\Gamma_{\text{in, }Z01}+D} \end{align} \]

Este mapeo tiene la forma de una transformada bilineal (Ecuación\(\eqref{eq:1}\)) con

\[\label{eq:6}A=1=D,\quad B=\frac{Z_{01}-Z_{02}}{Z_{01}+Z_{02}}=C \]

Dado que la ecuación\(\eqref{eq:5}\) es una transformada bilineal general, si el locus de\(\Gamma_{\text{in, }Z01}\) es un círculo, entonces el locus de también\(\Gamma_{\text{in, }Z02}\) es un círculo.

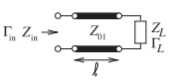
Figura\(\PageIndex{2}\): Línea de transmisión de impedancia característica\(Z_{01}\) terminada en una carga con coeficiente de reflexión\(\Gamma_{L}\).

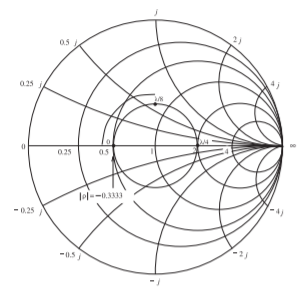
Figura\(\PageIndex{3}\): Un gráfico de Smith normalizado\(50\:\Omega\) con el locus del coeficiente de reflexión de entrada de una línea de\(50\:\Omega\) transmisión con una carga de\(25\:\Omega\).

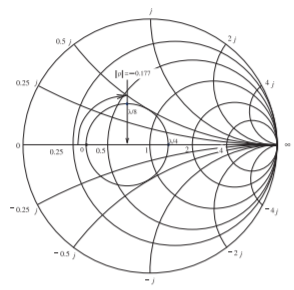
Figura\(\PageIndex{4}\): Un gráfico de Smith normalizado\(75\:\Omega\) con el locus del coeficiente de reflexión de entrada de una línea de\(50\:\Omega\) transmisión con una carga de\(25\:\Omega\).

Ejemplo\(\PageIndex{1}\): Reflection Coefficient, Reference Impedance Change

En el circuito de la derecha, una línea\(50-\Omega\) sin pérdidas se termina en una\(25-\Omega\) carga. Trazar el locus, con respecto a la longitud de la línea, del coeficiente de reflexión mirando dentro de la línea, haciendo referencia primero a una impedancia de\(50-\Omega\) referencia y luego a una impedancia de\(75-\Omega\) referencia.

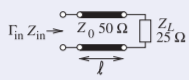
Figura\(\PageIndex{5}\)

Solución

Deje que el coeficiente de reflexión de entrada referenciado a un\(50-\Omega\) sistema sea\(\Gamma_{\text{in, }50}\), y cuando se hace referencia a\(75-\Omega\) él es\(\Gamma_{\text{in, }75}\). En el\(50-\Omega\) sistema el coeficiente de reflexión de la carga es

\[\label{eq:7}\Gamma_{L, 50}=\frac{Z_{L}-50}{Z_{L}+50}=\frac{25-50}{25+50}=-0.3333 \]

y

\[\label{eq:8}\Gamma_{\text{in, }50}=\Gamma_{L, 50}\text{e}^{-\jmath 2\theta} \]

donde\(\theta = (\beta\ell)\) está la longitud eléctrica de la línea. El locus, con respecto a la longitud eléctrica, de\(\Gamma_{\text{in, }50}\) se representa en la Figura\(\PageIndex{3}\) como la longitud\(\ell\) varía de\(0\)\(\lambda /8\) a\(\lambda /2\), y completa el círculo en\(\lambda /2\). Ahora

\[\label{eq:9}Z_{\text{in}}=50\frac{1+\Gamma_{\text{in, }50}}{1-\Gamma_{\text{in, }50}} \]

para que el coeficiente de\(75-\Omega\) reflexión sea

\[\label{eq:10}\Gamma_{\text{in, }75}=\frac{Z_{\text{in}}, 75}{Z_{\text{in}}+75} \]

El locus de este coeficiente de reflexión se grafica en una gráfica polar en la Figura\(\PageIndex{4}\). Este locus es la gráfica de\(\Gamma_{\text{in, }75}\) como la longitud eléctrica de la línea\(\theta\),, varía de\(0\) a\(π\). El centro del círculo en la Figura\(\PageIndex{4}\) se toma del gráfico y se determina que es\(−0.177\).

Un círculo se define por su centro y su radio, y las Ecuaciones ((1.239)) y ((1.240)) de [11], permiten que los círculos para el locus de\(\Gamma_{\text{in, }Z01}\) y\(\Gamma_{\text{in, }Z02}\) se relacionen. \(\Gamma_{\text{in, }Z01}\)tiene un centro\(C_{Z01}\) y un radio\(R_{Z01}\):

\[\label{eq:11}C_{Z01}=0\quad\text{and}\quad R_{Z01}=|\Gamma_{L, Z01}| \]

En la Ecuación ((1.239)) de [11]\(C_{Z01}\) reemplaza el centro\(C_{z}\) y\(|\Gamma_{L,Z01}|\) toma el lugar del radio\(R_{z}\). De igual manera el centro del\(\Gamma_{Z02}\) círculo\(C_{Z02}\),, reemplaza\(C_{w}\) y el radio del\(\Gamma_{Z02}\) círculo,\(R_{Z02}\), reemplaza\(R_{w}\). Entonces, el lugar geométrico del coeficiente de reflexión al que\(Z_{02}\) se hace referencia se describe mediante un círculo con centro y radio

\[\label{eq:12}C_{Z02}=\frac{B-A/C}{1-|C\text{T}_{L, Z01}|^{2}}+\frac{A}{C} \]

\[\label{eq:13}R_{Z02}=\left|\frac{(BC-A)\Gamma_{L, Z01}}{1-|C\text{T}_{L, Z01}|^{2}}\right| \]

Dado que, a partir de la Ecuación\(\eqref{eq:6}\),\(A = 1\) y\(B = C\) (\(B\)se da en la Ecuación\(\eqref{eq:6}\)), esto simplifica aún más a

\[\label{eq:14}C_{Z02}=\frac{B-1/B}{1-|B\Gamma_{L, Z01}|^{2}}+\frac{1}{B} \]

\[\label{eq:15}R_{Z02}=\left|\frac{(B^{2}-1)\Gamma_{L, Z01}}{1-|B\Gamma_{L, Z01}|^{2}}\right| \]

Entonces, el locus (con respecto a la frecuencia) del coeficiente de reflexión de entrada de una línea de transmisión terminada (de impedancia característica\(Z_{01}\)) es un círculo sin importar qué impedancia de normalización se use y el centro del círculo estará en el eje real, el eje horizontal del gráfico Smith.

Ejemplo\(\PageIndex{2}\): Center of Reflection Coefficient Locus

En Ejemplo\(\PageIndex{1}\) se\(75\:\Omega\) trazó el locus del coeficiente de reflexión de entrada al que se hace referencia para una\(50-\Omega\) línea terminada en una carga con coeficiente de reflexión (en el\(50-\Omega\) sistema) de\(−1/3\). Calcular el centro del coeficiente de reflexión de entrada cuando se hace referencia a él\(75\:\Omega\).

Solución

El centro del coeficiente de reflexión normalizado a\(Z_{01}\) es cero, es decir,\(C_{50} = 0\). A partir de la ecuación\(\eqref{eq:14}\), el centro del coeficiente de reflexión normalizado a\(Z_{02} = 75\:\Omega\) es

\[\label{eq:16}C_{75}=\frac{B-1/B}{1-|B\Gamma_{L, 50}|^{2}}+\frac{1}{B} \]

donde

\[\label{eq:17}B=\frac{Z_{01}-Z_{02}}{Z_{01}+Z_{02}}=\frac{50-75}{50+75}=-0.2 \]

Entonces

\[\label{eq:18}C_{75}=\frac{-0.2+5}{1-(0.2/3)^{2}}-5=-0.17857 \]

que se compara favorablemente con un centro de\(−0.177\) determinado manualmente a partir de la parcela polar en el ejemplo anterior.

3.5.3 Locus del coeficiente de reflexión

La dirección del lugar geométrico del coeficiente de reflexión de entrada de una línea de transmisión terminada es siempre en sentido horario con frecuencia creciente, incluso si el gráfico Smith utiliza una impedancia de referencia o normalización diferente de la impedancia característica de la línea. En la Figura\(\PageIndex{6}\),\(Z_{01}\) se encuentra la impedancia característica de la línea y\(Z_{02}\) es la impedancia de normalización. El centro del círculo del coeficiente de reflexión normalizado a\(Z_{02}\) está a la izquierda del origen si\(Z_{02} > Z_{01}\), y a la derecha del origen si se normaliza a\(Z_{02} < Z_{01}\), pero siempre en el eje real.

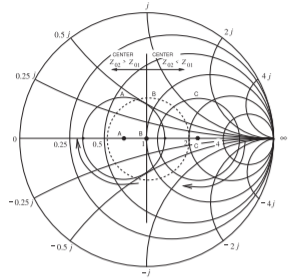
Figura\(\PageIndex{6}\): El locus del coeficiente de reflexión de entrada normalizado a\(Z_{02}\) de una línea terminada de impedancia característica\(Z_{01}\). El lugar es con respecto a la longitud eléctrica de la línea y las flechas muestran la dirección de rotación del coeficiente de reflexión. (Tenga en cuenta que para la misma impedancia de terminación los radios también cambiarán, pero esto no se muestra aquí).

3.5.4 Resumen

Los gráficos Smith son herramientas indispensables para los ingenieros de RF y microondas. Incluso con la disponibilidad de los programas CAD. Los gráficos Smith son generalmente preferidos para retratar datos medidos y calculados debido a la fácil interpretación de\(S\) los parámetros. Con experiencia, se pueden inferir las propiedades de los circuitos. Además, con experiencia son una herramienta de diseño invaluable que permite al diseñador ver los puntos iniciales y finales de un diseño e inferir el tipo de circuitos necesarios para ir de principio a fin.

Notas al pie

[1] Estos no son los\(ABCD\) parámetros en cascada, sino simplemente los coeficientes comúnmente utilizados con las transformaciones bilineales.