7.5: Transformadores Cónicos

Los transformadores de impedancia cónicos hacen coincidir una impedancia\(Z_{S}\) con una impedancia\(Z_{L}\) usando una línea de transmisión que tiene una impedancia característica\(Z_{0}\) que varía gradual y monótonamente de\(Z_{S}\) a\(Z_{L}\) lo largo de la longitud de la línea, ver Figura 7.4.7. Esta figura hace referencia a una línea de microcinta pero el aspecto clave es el cambio gradual en la impedancia característica que se aplica a cualquier línea de transmisión. El problema central del diseño es cómo elegir la función\(Z_{0}(z)\). Si la longitud de la línea,\(\ell\) aquí, no está restringida entonces el ahusamiento de Klopfentein [8, 9] se considera como el enfoque óptimo para el diseño del ahusamiento y se discutirá después de revisar primero los enfoques utilizados cuando la longitud de la línea está restringida. Tenga en cuenta que ambos\(Z_{L}\) y\(Z_{S}\) son resistivos.

7.5.1 Teoría de Reflexión Pequeña y Líneas Cónicas

En esta sección se desarrolla la teoría detrás de la síntesis de un ahusamiento comenzando con la teoría de las pequeñas reflexiones. La reflexión en el punto\(z\) de la línea para un segmento cónico de longitud\(\Delta z\) es (consulte la Figura 7.4.7 (a))

\[\label{eq:1}\Delta\Gamma=\frac{(Z_{0}(z)+\Delta z)-Z_{0}(z)}{(Z_{0}+\Delta Z)+Z_{0}(z)}=\frac{\Delta Z}{2Z_{0}(z)+\Delta Z}\approx\frac{\Delta Z}{2Z_{0}(z)} \]

donde\(Z_{0}(z)\) es la impedancia característica de la conicidad en\(z\) y\(\Delta Z\) es el cambio\(Z_{0}(z)\) de un lado del segmento ahusado al otro. En el límite como\(\Delta Z\to 0,\)\(\Delta Z\) se sustituye por\(dZ\) y\(\Delta\Gamma\) se sustituye por\(d\Gamma\) para que la Ecuación\(\eqref{eq:1}\) se convierta (y poniendo en forma de operador diferencial)

\[\label{eq:2}d\Gamma=\frac{dZ_{0}}{2Z_{0}(z)}\quad\to\quad\frac{d\Gamma}{dz}=\frac{\text{d}\Gamma}{\text{d}z}=\frac{1}{2Z_{0}(z)}\frac{\text{d}Z_{0}}{\text{d}z} \]

El siguiente paso es referir todos los pequeños reflejos,\(\Delta\Gamma\), al inicio de la conicidad en\(z = −\ell /2\). La teoría de las pequeñas reflexiones es que estas pequeñas reflexiones, que dan cuenta de las longitudes eléctricas desde el inicio del ahusamiento hasta cada segmento cónico, se pueden sumar, véase la Ecuación (7.4.3). Esto es lo mismo que decir que la pequeña reflexión de un segmento cónico no se ve afectada por su propia reflexión de otro segmento cónico. Observando que la longitud eléctrica desde el inicio del ahusamiento hasta un segmento cónico en\(z\) es\(\theta = \beta(\ell /2 + z)\), la reflexión en la entrada de la línea cónica se encuentra como

\[\begin{align}\label{eq:3}\Gamma_{\text{in}}(\ell)&=\int_{z=-\ell /2}^{z=\ell /2}\text{e}^{-2\jmath (\ell/2+\beta z)}\text{d}\Gamma \\ \label{eq:4}&=\frac{1}{2}\text{e}^{-\jmath\beta\ell}\int_{-\ell/2}^{\ell/2}\frac{\text{e}^{-2\jmath\beta z}}{Z_{0}(z)}\frac{\text{d}Z_{0}(z)}{\text{d}z}\text{d}z\end{align} \]

donde\(\Gamma_{\text{in}}\) se muestra explícitamente como una función de la longitud del ahusamiento. Entonces el problema de diseño se convierte en elegir la función de impedancia característica,\(Z_{0}(z)\) para proporcionar el coeficiente de reflexión de entrada deseado\(\Gamma_{\text{in}}\). Esto es difícil de lograr con la forma de Ecuación\(\eqref{eq:4}\). El problema puede simplificarse señalando que (e introduciendo\(Z_{1}\) como impedancia normalizadora para que el argumento de\(\ln\) sea adimensional)

\[\begin{align}\frac{\ln (Z_{0}(z)/Z_{1})}{\text{d}z}&=\frac{Z_{1}}{Z_{0}(z)}\frac{\text{d}(Z_{0}(z)/Z_{1})}{\text{d}z}=\frac{Z_{1}}{Z_{0}(z)}\frac{1}{Z_{1}}\frac{\text{d}(Z_{0}(z)/Z_{1})}{\text{d}z}\nonumber \\ \label{eq:5}&=\frac{1}{Z_{0}(z)}\frac{\text{d}(Z_{0}(z)/Z_{1})}{\text{d}z}\end{align} \]

y así, dejando claro que\(d\Gamma\) varía a lo largo de la conicidad,

\[\label{eq:6}d\Gamma (z)=\frac{1}{2}\frac{\text{d}(Z_{0}(z)/Z_{1})}{\text{d}z}dz \]

Así, después de asumir la forma de\(Z_{0}(z)\), el coeficiente de reflexión incremental\(d\Gamma\) se obtiene usando Ecuación\(\eqref{eq:3}\). Alternativamente (después de integrar Ecuación\(\eqref{eq:6}\)) una forma para\(\Gamma_{\text{in}}\) puede ser asumida y\(d\Gamma (z)\) determinada y luego\(Z_{0}(z)\). Esto se aclarará a continuación cuando se consideren los ahusamientos específicos.

7.5.2 Cono lineal

En la línea cónica lineal el diseño\(Z_{0}(z)\) varía linealmente de la impedancia de la fuente\(Z_{S}\) a\(Z_{L}\):

\[\label{eq:7}Z_{0}(z)=Z_{S}+(Z_{L}-Z_{S})z/\ell \]

Esto a menudo se aproxima en microcinta por un ahusamiento lineal del ancho de la línea de microcinta como se muestra en la Figura 7.4.7 (b). Una expresión simple para el coeficiente de reflexión de entrada no está disponible y, por lo tanto, debe encontrarse a partir de la simulación.

Este es el cono más simple y el ahusamiento funciona mejor cuanto mayor sea su longitud eléctrica (es decir, a frecuencias más altas o longitud física más larga). El rendimiento del ahusamiento lineal se compara con otros ahusamientos posteriores.

7.5.3 Cono exponencial

El ahusamiento exponencial tiene un ahusamiento exponencial de la impedancia característica de la línea. Ajuste

\[\label{eq:8}Z_{0}(z)=Z_{x}\text{e}^{az}\quad\text{with}\quad a=\frac{1}{\ell}\ln (Z_{L}/Z_{S})\quad\text{and}\quad Z_{x}=Z_{S}\text{e}^{-a\ell /2} \]

resultados en el coeficiente de reflexión de entrada, derivado usando Ecuación\(\eqref{eq:4}\),

\[\label{eq:9}\Gamma_{\text{in}}(\ell)=\frac{1}{2}Z_{x}\text{e}^{-\jmath\beta\ell}\int_{-\ell/2}^{\ell/2}\text{e}^{-2\jmath\beta z}\frac{\text{d}\ln(\text{e}^{az})}{\text{d}z}\text{d}z=\frac{1}{2}\ln(Z_{L}/Z_{S})\frac{\sin(\beta\ell)}{\beta\ell} \]

Así\(\Gamma_{\text{in}}\) tiene una característica de función sinc con las variaciones de\(\Gamma_{\text{in}}\) reducción a medida que el ahusamiento se hace más largo. El principal problema con este ahusamiento proviene de la abrupta discontinuidad de impedancia al\(Z_{L}\) final del ahusamiento. Este ahusamiento no se considerará más lejos ya que el cono Klopfenstein considerado a continuación tiene un rendimiento mucho mejor.

7.5.4 Cono Klopfenstein

La conicidad de Klopfenstein [8, 9] da como resultado una ondulación de coeficiente de reflexión especificada (y por lo tanto ondulación de transmisión) por encima de una frecuencia mínima de banda Se cree que logra la longitud mínima de conicidad sobre una banda de paso definida por el desajuste máximo permisible del coeficiente de reflexión,\(\Gamma_{m}\), (y por lo tanto la pérdida mínima de transmisión) en la banda de paso. El ahusamiento lineal y la mayoría de los otros ahusamientos utilizados en la coincidencia [10, 11] asumen la forma del perfil de impedancia característico de un ahusamiento y las características de reflexión y transmisión de banda ancha son los resultados. En contraste, el cono de Klopfenstein deriva el perfil de impedancia requerido para una relación de desajuste de impedancia de fuente y carga\((Z_{L}/Z_{S})\) y\(\Gamma_{m}\).

Klopfenstein [8] mostró que el coeficiente de reflexión de entrada del ahusamiento podría expresarse como la forma limitante de un polinomio de Chebyshev de orden superior. Por lo tanto, el cono Klopfenstein tiene las ondas de banda de paso que ocurren con los transformadores de impedancia de múltiples secciones basados en Chebyshev y los filtros Chebyshev. La magnitud máxima del coeficiente de reflexión en la banda de paso está determinada por la longitud de línea. La impedancia característica apropiada se calcula a partir de [8, 9]

\[\begin{align}\ln Z_{0}(z)&=\ln\left(\sqrt{Z_{S}Z_{L}}\right)+\ln\left(\sqrt{Z_{L}/Z_{S}}\right)\cdot (\cosh A)^{-1} \nonumber \\ \label{eq:10}&\quad\times [A^{2}\phi(2z/\ell,A)+U(z-\frac{1}{2}\ell)+U(z+\frac{1}{2}\ell)-1]\end{align} \]

donde\(U(x)\) esta la función de paso de unidad\(U(x)=0\) para que para\(x < 0\) y\(U(x)=1\) para\(x\geq 0\).

La amplitud máxima del coeficiente de reflexión\(\Gamma_{m} = \rho_{0}/ \cosh\:A\) donde\(\rho_{0} = (Z_{L} − Z_{S}/(Z_{L} + Z_{S})\) es el coeficiente de reflexión cuando la carga y la fuente están conectadas directamente. Klopfenstein encontró que esto introdujo un pequeño error atribuido a la limitación de la suposición de reflexión pequeña. Determinó que una mejor estimación es\(\rho_{0} =\frac{1}{2}\ln (Z_{L}/Z_{S})\). Así

\[\label{eq:11}A=\cosh^{-1}[\ln(Z_{L}/Z_{S})/\Gamma_{m}] \]

Es decir\(\Gamma_{m}\), el coeficiente de reflexión máximo en la banda de paso, y el desajuste,\(Z_{L}/Z_{S}\), determina\(A\). Sustitución de ecuaciones\(\eqref{eq:11}\) en\(\eqref{eq:10}\) rendimientos de ecuaciones

\[\begin{align}\ln Z_{0}(z)&=\ln\left(\sqrt{Z_{S}Z_{L}}\right)+\ln\left(\sqrt{Z_{L}/Z_{S}}\right)\Gamma_{m}\frac{(Z_{L}+Z_{S})}{(Z_{L}-Z_{S})} \nonumber \\ \label{eq:12}&\quad\times\left[ A^{2}\phi (2x/\ell, A)+U(z-\frac{1}{2}\ell)+U(z+\frac{1}{2}\ell)-1\right]\end{align} \]

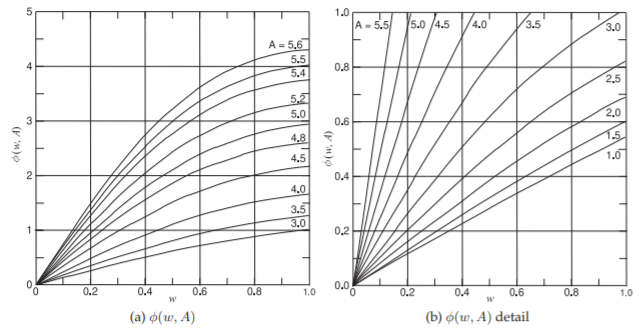
Figura\(\PageIndex{1}\): Función cónica de Klopfenstein\(\phi (w, A)\) utilizada en el diseño de un segmento cónico. El ahusamiento tiene longitud\(\ell,\: z\) es la coordenada en el centro de un segmento cónico, el centro del ahusamiento está en\(z = 0\), y\(\phi(−w,\: A) = −\phi (w,\: A),\: w = 2z/\ell\).

y la función\(\phi (w,\: A)\) se calcula como [12]

\[\label{eq:13}\phi(w,\:A)=\sum_{k=0}^{\infty}a_{k}b_{k} \]

(la suma hasta\(k = 20\) es suficiente) con las fórmulas de recursión

\[\label{eq:14}a_{0}=1,\: a_{k}=\frac{A^{2}}{4k(k+1)}a_{k-1};\quad b_{0}=\frac{1}{2}w,\quad b_{k}=\frac{\frac{1}{2}w(1-w^{2})^{k}+2kb_{k-1}}{2k+1} \]

Los resultados se muestran en la Figura\(\PageIndex{1}\).

Es interesante derivar la impedancia característica en el centro del ahusamiento. En el centro de la conicidad,\(z = 0,\:\phi (0,\: A)=0\) y la ecuación\(\eqref{eq:10}\) se convierte

\[\label{eq:15}\ln Z_{0}(0)=\frac{1}{2}\ln(Z_{S}Z_{L}),\quad\text{that is,}\quad Z_{0}(0)=\sqrt{Z_{S}Z_{L}} \]

que es la media geométrica de las resistencias de fuente y carga.

El cono Klopfenstein comercializa la longitud fuera de línea\(\ell\), la frecuencia\(f_{\text{min}}\) mínima de banda de paso y el coeficiente\(\Gamma_{m}\) máximo de reflexión de banda de paso La banda de paso del ahusamiento es todas las frecuencias anteriores\(f_{\text{min}}\). Este es un resultado notable con la longitud de la línea siendo considerablemente menor que la de un ahusamiento lineal. La limitación es que con una línea tan corta las reflexiones a lo largo de la línea no siempre pueden considerarse pequeñas por lo que a menudo es necesario aumentar la longitud de la línea ligeramente por encima de la longitud derivada de este procedimiento de síntesis.

7.5.5 Cono Klopfenstein simplificado

La forma simplificada de la conicidad de Klopfenstein se obtiene señalando que el valor aceptable para el coeficiente máximo de reflexión en banda\(\Gamma_{m}\) será

\(w\)	Exacto \(Z_{0}(w)/Z_{S}\)	Simplificado \(Z_{0}(w)/Z_{S}\)	Error
\ (w\) ">\(-1.0\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.163\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.177\)	\(1.23\%\)
\ (w\) ">\(-0.8\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.326\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.344\)	\(1.32\%\)
\ (w\) ">\(-0.6\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.577\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.597\)	\(1.26\%\)
\ (w\) ">\(-0.4\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.944\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(1.964\)	\(1.04\%\)
\ (w\) ">\(-0.2\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(2.460\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(2.476\)	\(0.64\%\)
\ (w\) ">\(0.0\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(3.162\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(3.162\)	\(0\%\)
\ (w\) ">\(0.2\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(4.065\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(4.039\)	\(0.64\%\)
\ (w\) ">\(0.4\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(5.145\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(5.092\)	\(1.03\%\)
\ (w\) ">\(0.6\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(6.214\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(6.262\)	\(1.25\%\)
\ (w\) ">\(0.8\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(7.539\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(7.440\)	\(1.31\%\)
\ (w\) ">\(1.0\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(8.520\)	\ (Z_ {0} (w) /Z_ {S}\) ">\(8.542\)	\(1.12\%\)

Tabla\(\PageIndex{1}\): Comparación\(Z_{0}\) de los ahusamientos exactos y simplificados de Klopfenstein (usando Ecuación\(\eqref{eq:12}\) con Ecuaciones\(\eqref{eq:13}\) y\(\eqref{eq:16}\) respectivamente) para una pérdida de transmisión de banda de paso máxima\(T_{m} = 0.1\text{ dB}\) y\(Z_{L}/Z_{S} = 10\)\((\Gamma_{m} = 0.151\) y Los\(A = 2.72.)\) errores son menores para mayores\(T_{m}\) y menor\(Z_{L}/Z_{S}\):
Para\(Z_{L}/Z_{S} = 20,\: T_{m} = 0.1\text{ dB}\), el error máx. es\(2.78\%\).
Para\(Z_{L}/Z_{S} = 20,\: T_{m} = 0.2\text{ dB}\), el error máx. es\(1.49\%\).
Para\(Z_{L}/Z_{S} = 10,\: T_{m} = 0.1\text{ dB}\), el error máx. es\(1.33\%\).
Para\(Z_{L}/Z_{S} = 10,\: T_{m} = 0.2\text{ dB}\), el error máx. es\(0.66\%\).
Para\(Z_{L}/Z_{S} = 5,\: T_{m} = 0.1\text{ dB}\), el error máx. es\(0.44\%\).
Para\(Z_{L}/Z_{S} = 5,\: T_{m} = 0.2\text{ dB}\), el error máx. es\(0.21\%\).

típicamente ser pequeños y para una pérdida de transmisión máxima de entre\(0.1\text{ dB}\) y\(1\text{ dB}\) (correspondiente a\(\Gamma_{m} = 0.151\) y\(\Gamma_{m} = 0.454\) respectivamente) y máxima\(Z_{L}/Z_{S} = 10\). Entonces el valor máximo de\(A\) es\(2.72\) y esto es cuando el cono simplificado de Klopfenstein tendrá el mayor error. Así que conservando solo los tres primeros términos en la Ecuación\(\eqref{eq:13}\), se\(\phi(w,\: A)\) puede aproximar como

\[\label{eq:16}\phi(w,\: A)=a_{0}b_{0}+a_{1}b_{1}+a_{2}b_{2} \]

y se utiliza en la Ecuación\(\eqref{eq:12}\). Una comparación de las impedancias calculadas para una pérdida de transmisión relativamente alta de\(1\text{ dB}\) (\(0.1\text{ dB}\)es más típica) y una gran falta de coincidencia de impedancia\(Z_{L}/Z_{S} = 10\) se da en la Tabla\(\PageIndex{1}\). El error máximo de\(1.33\%\) es comparable al error de impedancia característico de las líneas de transmisión fabricadas. Entonces, para fines prácticos, se puede utilizar el enfoque simplificado para diseñar el cono Klopfenstein.

Ejemplo\(\PageIndex{1}\): Design of a Klopfenstein Taper

Diseñe un cono Klopfenstein de microcinta para hacer coincidir una\(Z_{S} = 10\:\Omega\) fuente con una\(Z_{L} = 50\:\Omega\) carga. La ondulación máxima de transmisión debe ser\(0.1\text{ dB}\) y la frecuencia mínima de banda de paso es\(8\text{ GHz}\). El sustrato tiene un espesor\(h = 0.635\:\mu\text{m}\), y permitividad relativa\(\varepsilon_{r} = 10.0\).

Solución

Primero determinar el coeficiente de reflexión máximo\(\Gamma_{m}\) en la banda de paso. La transmisión mínima en la banda de paso es\(T = 10^{0.1/20}\) y\(\Gamma_{m} =\sqrt{1 − T^{2}} = 0.151\). \(Z_{L}/Z_{S} = 5\)Ya que se ve de la Tabla\(\PageIndex{1}\) que el cono simplificado de Klopfenstein se puede utilizar con un error máximo de\(1.33\%\). Usando\(\eqref{eq:11}\) la ecuación, la longitud eléctrica requerida del cono en\(8\text{ GHz}\) es

\[A=\cosh^{-1}[\ln(Z_{L}/Z_{S})/\Gamma_{m}]=\cosh^{-1}[\ln(50/5)/0.151]=2.720\nonumber \]

Se elige un ahusamiento con diez segmentos y en la tabla siguiente\(w′ = 2z/\ell\) se utiliza la longitud normalizada para distinguir el parámetro del ancho de la microcinta\(w\). Los parámetros de microcinta se obtuvieron interpolando el Cuadro 3-3 de [6]. \(\overline{Z}_{0}\)y\(\overline{\varepsilon}_{e}\) son la impedancia característica promedio y la permitividad efectiva de un segmento, un ahusamiento lineal, que se extiende desde el ancho en la línea anterior hasta el de la misma línea. La longitud eléctrica de cada segmento es\(\beta (\Delta\ell ) = A/10 = 0.272\text{ radians}\) tal que la longitud física de un segmento\(\ell = 0.272\lambda_{8\text{ GHz}}/(2π\sqrt{\varepsilon_{e}})\) donde\(\lambda_{8\text{ GHz}} = 3.745\text{ cm}\) está la longitud de onda del espacio libre en\(8\text{ GHz}\).

Segmento	\(w'\)	\(\phi (w',\: A)\)	\(Z_{0}\:(\Omega )\)	\(u=h/w\)	\(w\text{ (mm)}\)	\(\overline{Z}_{0}\:(\Omega)\)	\(\overline{\varepsilon}_{e}\)	\(\Delta\ell\text{ (}\mu\text{m)}\)
	\ (w'\) ">\(-1.0\)	\ (\ phi (w',\: A)\) ">\(−0.774\)	\ (Z_ {0}\: (\ Omega)\) ">\(11.68\)	\ (u=h/w\) ">\(8.28\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">	\ (\ overline {\ varepsilon} _ {e}\) ">	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(1\)	\ (w'\) ">\(-0.8\)	\ (\ phi (w',\: A)\) ">\(−0.661\)	\ (Z_ {0}\: (\ Omega)\) ">\(12.84\)	\ (u=h/w\) ">\(7.38\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(12.2\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(8.35\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(2\)	\ (w'\) ">\(-0.6\)	\ (\ phi (w',\: A)\) ">\(−0.521\)	\ (Z_ {0}\: (\ Omega)\) ">\(14.44\)	\ (u=h/w\) ">\(6.39\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(14.1\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(8.19\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(3\)	\ (w'\) ">\(-0.4\)	\ (\ phi (w',\: A)\) ">\(−0.360\)	\ (Z_ {0}\: (\ Omega)\) ">\(16.52\)	\ (u=h/w\) ">\(5.40\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(16.0\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(8.05\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(4\)	\ (w'\) ">\(-0.2\)	\ (\ phi (w',\: A)\) ">\(−0.184\)	\ (Z_ {0}\: (\ Omega)\) ">\(19.16\)	\ (u=h/w\) ">\(4.45\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(17.8\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(7.93\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(5\)	\ (w'\) ">\(0\)	\ (\ phi (w',\: A)\) ">\(0\)	\ (Z_ {0}\: (\ Omega)\) ">\(22.36\)	\ (u=h/w\) ">\(3.62\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(20.8\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(7.75\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(6\)	\ (w'\) ">\(0.2\)	\ (\ phi (w',\: A)\) ">\(0.184\)	\ (Z_ {0}\: (\ Omega)\) ">\(26.10\)	\ (u=h/w\) ">\(2.90\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(24.7\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(7.54\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(7\)	\ (w'\) ">\(0.4\)	\ (\ phi (w',\: A)\) ">\(0.360\)	\ (Z_ {0}\: (\ Omega)\) ">\(30.26\)	\ (u=h/w\) ">\(2.33\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(28.7\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(7.35\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(8\)	\ (w'\) ">\(0.6\)	\ (\ phi (w',\: A)\) ">\(0.521\)	\ (Z_ {0}\: (\ Omega)\) ">\(34.63\)	\ (u=h/w\) ">\(1.88\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(32.9\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(7.18\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(9\)	\ (w'\) ">\(0.8\)	\ (\ phi (w',\: A)\) ">\(0.661\)	\ (Z_ {0}\: (\ Omega)\) ">\(38.93\)	\ (u=h/w\) ">\(1.54\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(37.3\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(7.03\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">
\(10\)	\ (w'\) ">\(1.0\)	\ (\ phi (w',\: A)\) ">\(0.774\)	\ (Z_ {0}\: (\ Omega)\) ">\(42.83\)	\ (u=h/w\) ">\(1.29\)	\ (w\ texto {(mm)}\) ">	\ (\ overline {Z} _ _ {0}\: (\ Omega)\) ">\(41.4\)	\ (\ overline {\ varepsilon} _ {e}\) ">\(6.90\)	\ (\ Delta\ ell\ texto {(}\ mu\ texto {m)}\) ">

Mesa\(\PageIndex{2}\)

También en\(w = (−1.0 − 1/∞) Z_{0} = 510.03\:\Omega\) y al\(w = (1.0+1/∞) Z_{0} = 49.81\:\Omega\) hacer coincidir las impedancias de fuente y carga respectivamente y por lo tanto hay una discontinuidad escalonada en ambos extremos, una característica de la conicidad de Klopfenstein.

7.5.6 Comparación de transformadores de impedancia de línea de transmisión

En esta sección se comparan los cuatro transformadores de impedancia principales: el cono lineal, el cono Klopfenstein, el transformador de cuarto de onda y el transformador de cuarto de onda de dos secciones. Estos transformadores son longitudes de línea de transmisión no uniforme con una impedancia característica que varía a lo largo de la longitud de la línea, es decir,\(Z_{0} = Z_{0}(z)\) dónde\(z\) está la posición a lo largo de la línea de longitud total\(\ell\). El transformador\(N\) de cuarto de onda de sección tiene cambios escalonados\(Z_{0}(z)\) en\(n\lambda /4\) donde\(n = 1, 2 <\ldots N\) pero prácticamente\(N = 1\) o\(2\) es el límite generalmente considerado ya que se puede obtener un rendimiento mucho mejor con el cono Klopfenstein con una legth típicamente entre\(\lambda /4\) y \(\lambda /2\). La figura\(\PageIndex{2}\) compara el desempeño de los ahusamientos para\(Z_{S} = 25\:\Omega\) y\(Z_{L} = 50\:\Omega\) pero los resultados son aplicables en general para\(Z_{L}/Z_{S} = 2\). La figura\(\PageIndex{2}\) (a) muestra el\(Z_{0}\) perfil para los transformadores de línea de transmisión y donde se ha elegido la longitud del ahusamiento lineal para proporcionar respuestas de banda de paso comparables definidas como donde la pérdida de transmisión es menor que la\(0.1\text{ dB}\) correspondiente a un coeficiente de reflexión máximo \(\Gamma_{m} = 0.151\)y un factor mínimo de transmisión\(T = 0.989\). La respuesta del coeficiente de reflexión se muestra en la Figura\(\PageIndex{2}\) (b). Primero considere las respuestas de los transformadores de cuarto de onda. Ambos proporcionan una coincidencia ideal en la frecuencia central de banda de paso\(f_{0} = 10\text{ GHz}\) y esto se repite en múltiplos impares de\(f_{0}\) como una línea\(3\lambda /4\) -larga es eléctricamente idéntica a una línea\(\lambda /4\) -larga. El ahusamiento lineal, elegido aquí\(\lambda_{m}/2\) siempre que\(\lambda_{m}\) esté la longitud de onda guía\(f_{0}\), tiene un desajuste del coeficiente de reflexión que se reduce a medida que aumenta la frecuencia a medida que la línea se vuelve eléctricamente más larga.

El cono de Klopfenstein para\(\Gamma_{m} = 0.151\) y\(Z_{L}/Z_{S} = 2\) tiene\(A = 1.1103\) tal que la banda de paso del cono Klopfenstein se extiende indefinidamente por encima de una longitud eléctrica de 1.1103 radianes que define la longitud física de la línea para una frecuencia de banda de paso mínima elegida\(f_{\text{min}}\). La elección de diseño aquí es\(f_{\text{min}} = 0.532f_{0}\) así que\(f_{\text{min}}\) fue comparable a la del transformador de cuarto de onda de dos secciones. Entonces la longitud de la línea eléctrica requerida es\(0.87\lambda_{m}/2\). Es decir, un cono Klopfenstein ligeramente más corto tiene la misma frecuencia mínima de banda de paso que un transformador de cuarto de onda de dos secciones.

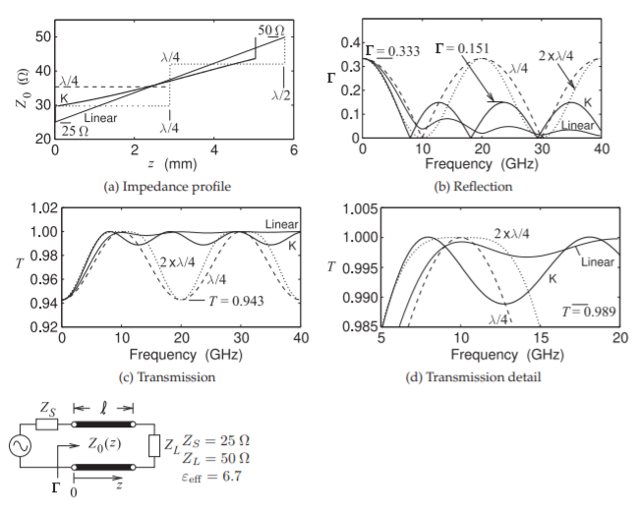
Figura\(\PageIndex{2}\): Características de los transformadores de línea de transmisión simulados. Longitud de onda de banda media\(\lambda_{m} = 11.58\text{ mm}\) en\(f_{0} = 10\text{ GHz}\). Lineal: Cono lineal,\(\ell = \lambda_{m}/2\). \(\lambda/4\):\(\lambda/4\) transformador,\(\ell = \lambda_{m}/4\). \(2x\lambda /4\):\(\lambda/4\) transformador de dos secciones,\(\ell = \lambda_{m}/2\). \(\text{K}\): Cono Klopfenstein,\(\ell = 3.88\text{ mm} = 0.335\lambda_{m}\).

El cono Klopfenstein tiene la clara ventaja de que la banda de paso se extiende indefinidamente por encima de\(f_{\text{min}}\) donde los transformadores de una etapa y de múltiples etapas de cuarto de onda tienen un ancho de banda finito.

El párrafo anterior consideró coincidir cuando\(Z_{L}/Z_{S} = 2\). Una comparación similar se muestra en la Figura\(\PageIndex{3}\) para una discontinuidad de impedancia de fuente y carga mucho mayor con\(Z_{S} =5\:\Omega\)\(Z_{L} = 50\:\Omega\) y y los resultados son aplicables en general para\(Z_{L}/Z_{S} = 10\). La figura\(\PageIndex{3}\) (a) muestra el\(Z_{0}\) perfil para los transformadores de línea de transmisión y donde se ha elegido la longitud del ahusamiento lineal para proporcionar respuestas de banda de paso comparables definidas como donde la pérdida de transmisión es menor que\(0.1\text{ dB}\) (correspondiente a una magnitud de coeficiente de reflexión máxima de\(0.151\)). La respuesta del coeficiente de reflexión se muestra en la Figura\(\PageIndex{3}\) (b). Primero considere las respuestas de los transformadores de una y dos secciones de cuarto de onda. Ambos proporcionan una coincidencia ideal en la frecuencia central de la banda de paso\(f_{0} = 10\text{ GHz}\) y se repiten en múltiplos impares de\(f_{0}\).

Nuevamente, la banda de paso definida por el transformador de cuarto de onda de dos secciones se usa para determinar la longitud de los ahusamientos lineales y Klopfenstein, lo que resulta en que el ahusamiento lineal es\(3\lambda_{m}\) largo y el cono Klopfenstein es\(0.595\lambda_{m}\) largo, ligeramente más largo que el transformador de cuarto de onda de dos secciones. El ahusamiento lineal, elegido aquí para ser\(\lambda_{m}/2\) largo donde\(\lambda_{m}\) está la longitud de onda guía\(f_{0}\), tiene un desajuste del coeficiente de reflexión que se reduce a medida que aumenta la frecuencia

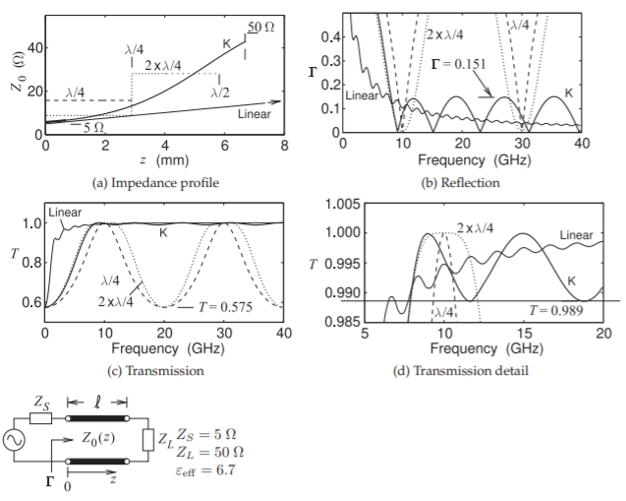
Figura\(\PageIndex{3}\): Características de los transformadores de línea de transmisión simulados. Longitud de onda de banda media\(\lambda_{m} = 11.58\text{ mm}\) en\(f_{0} = 10\text{ GHz}\). Lineal: Cono lineal,\(\ell = \lambda_{m}/2\). \(\lambda/4\):\(\lambda/4\) transformador,\(\ell = \lambda_{m}/4\). \(2x\lambda/4\):\(\lambda/4\) transformador de dos secciones,\(\ell = \lambda_{m}/2\). \(K\): Cono Klopfenstein,\(\ell = 3.88\text{ mm} = 0.335\lambda_{m}\).

\(Z_{L}/Z_{S}=2\)	\(\ell\)	Passband	Ancho de banda
\ (Z_ {L} /Z_ {S} =2\)” class="LT-ENG-41147">Cono lineal	\ (\ ell\)” class="lt-eng-41147">\(0.5\lambda_{m}\)	\(>6.53\text{ GHz}\)
\ (Z_ {L} /Z_ {S} =2\)” class="lt-eng-41147">\(\lambda/4\)	\ (\ ell\)” class="lt-eng-41147">\(0.25\lambda_{m}\)	\(7.16-11.84\text{ GHz}\)	\(50\%\)
\ (Z_ {L} /Z_ {S} =2\)” class="lt-eng-41147">\(2\times\lambda/4\)	\ (\ ell\)” class="lt-eng-41147">\(0.5\lambda_{m}\)	\(5.43-14.57\text{ GHz}\)	\(91\%\)
\ (Z_ {L} /Z_ {S} =2\)” class="LT-ENG-41147">Cono Klopfenstein	\ (\ ell\)” class="lt-eng-41147">\(0.335\lambda_{m}\)	\(>5.43\text{ GHz}\)
\(Z_{L}/Z_{S}=10\)
\ (Z_ {L} /Z_ {S} =2\)” class="LT-ENG-41147">Cono lineal	\ (\ ell\)” class="lt-eng-41147">\(3\lambda_{m}\)	\(>7.72\text{ GHz}\)
\ (Z_ {L} /Z_ {S} =2\)” class="lt-eng-41147">\(\lambda/4\)	\ (\ ell\)” class="lt-eng-41147">\(0.25\lambda_{m}\)	\(9.32-10.69\text{ GHz}\)	\(14\%\)
\ (Z_ {L} /Z_ {S} =2\)” class="lt-eng-41147">\(2\times\lambda/4\)	\ (\ ell\)” class="lt-eng-41147">\(0.5\lambda_{m}\)	\(7.87-12.12\text{ GHz}\)	\(42\%\)
\ (Z_ {L} /Z_ {S} =2\)” class="LT-ENG-41147">Cono Klopfenstein	\ (\ ell\)” class="lt-eng-41147">\(0.595\lambda_{m}\)	\(>7.87\text{ GHz}\)
\ (Z_ {L} /Z_ {S} =2\)” class="LT-ENG-41147">Cono exponencial	\ (\ ell\)” class="lt-eng-41147">\(1.68\lambda_{m}\)	\(>7.87\text{ GHz}\)

Tabla\(\PageIndex{3}\): Comparación de bandas de paso de los cuatro transformadores de impedancia de línea de transmisión considerados en la Sección 7.5.6 con\(\lambda_{m}\) ser la longitud de onda guía at\(10\text{ GHz}\). Las longitudes de los ahusamientos se eligieron para tener la misma frecuencia mínima de banda de paso que el transformador de cuarto de onda de dos secciones.

a medida que la línea se vuelve eléctricamente más larga.

El cono Klopfenstein para\(\Gamma_{m} = 0.151\) y\(Z_{L}/Z_{S} = 10\) tiene de\(A = 2.720\) manera que la banda de paso del cono Klopfenstein se extiende indefinidamente por encima de una longitud eléctrica de\(2.720\) radianes y así elegir la frecuencia mínima de banda de paso\(f_{\text{min}}\) determina la longitud física de la línea.

\(0.1\text{ dB}\)Las bandas de paso de los transformadores de línea de transmisión se comparan en la Tabla\(\PageIndex{3}\). El transformador de cuarto de onda de dos secciones y el transformador Klopfenstein tienen un rendimiento comparable cerca de la frecuencia central del diseño, con la elección de si es más importante tener buenas propiedades de transmisión indefinidamente por encima\(f_{\text{min}}\) o proporcionar alguna selectividad de frecuencia al tener una coincidencia más pobre en la segunda frecuencia armónica de la frecuencia de coincidencia central, aquí\(f_{0}\).

7.5.7 Resumen

Los transformadores de línea de transmisión considerados en esta sección coinciden con las impedancias de carga y fuente resistiva. Sin embargo, estos transformadores de impedancia proporcionan orientación para estrategias de diseño cuando la fuente y la carga incluyen reactancias. Cuando la fuente y la carga son resistencias, la elección clara para un transformador de impedancia basado en línea de transmisión es la cinta Klopfenstein. Con una carga reactiva, el desafío es lograr la coincidencia de banda ancha ya que, por supuesto, la reactancia de la carga y/o carga variará con la frecuencia y así impondrá una restricción general de ancho de banda. El diseño de la red coincidente debe tener en cuenta la característica de frecuencia de la carga.

Diferentes cargas tendrán diferentes características de frecuencia y, por lo tanto, variaciones en el tipo de red de coincidencia requerida. Cuatro cargas básicas que se encuentran comúnmente en la ingeniería de microondas y a las que se requiere coincidencia incluyen el modelo RC en serie de la entrada de un transistor FET con una reactancia en serie que es inversamente proporcional a la frecuencia; el modelo LR en serie que se encuentra en la unión a la entrada de un dispositivo donde el la inductancia proviene de un cable de unión y que tiene una reactancia en serie que es proporcional a la frecuencia; y una carga RC paralela que se encuentra en la salida de un transistor con una susceptancia que se reduce con la frecuencia. Estos modelos de fuentes y cargas de dos elementos son simples y es posible que sea necesario incluir otros parásitos. A frecuencias de microondas, la\(Q\) de las impedancias encontradas con los dispositivos activos está típicamente en el rango de\(0.5\) a\(3\), y la falta de coincidencia de resistencia fuente/carga típicamente varía de\(1.5\) a\(10\). Por ejemplo, se encuentran desajustes altos en la salida de los amplificadores de potencia.