2.2: Teoría de Líneas de Transmisión

En esta sección se desarrolla la teoría de la propagación de señales en líneas de transmisión. La primera sección, Sección 2.2.1, argumenta que un circuito con resistencias, inductores y capacitores es un buen modelo para una línea de transmisión. El desarrollo completo de la teoría de líneas de transmisión se presenta en la Sección 2.2.2, y la Sección 2.2.3 relaciona el modelo de línea de transmisión RLGC con las propiedades de un medio. Las dimensiones de algunas de las cantidades que aparecen en la teoría de líneas de transmisión se discuten en la Sección 2.2.4. La Sección 2.2.5 resume los parámetros importantes de una línea sin pérdidas y luego dos líneas particularmente importantes, líneas coaxiales y líneas de microcinta, se consideran en las Secciones 2.2.6 y 2.2.7.

2.2.1 Línea de Transmisión Modelo RLGC

Independientemente de la estructura real, un segmento de línea de transmisión uniforme (es decir, una línea con sección transversal constante a lo largo de su longitud) como se muestra en la Figura\(\PageIndex{1}\) (a) puede modelarse mediante el circuito mostrado en la Figura\(\PageIndex{1}\) (b) con

\[\left.\begin{array}{lr}{\text{Resistance along the line}}&{=R} \\ {\text{Inductance along the line}}&{=L} \\ {\text{Conductance shunting the line}}&{=G} \\ {\text{Capacitance shunting the line}}&{=C}\end{array}\right| \begin{array}{l}{}\\{\text{all specified}} \\ {\text{per unit length}}\\{}\end{array}\nonumber \]

Así\(R,\: L,\: G\), y también\(C\) se les conoce como resistencia, inductancia, conductancia y capacitancia por unidad de longitud. (A veces p.u.l. se usa como abreviatura de por unidad de longitud.) En el sistema métrico se utilizan ohmios por metro (\(Ω\text{/m}\)), henries por metro (\(\text{H/m}\)), siemens por metro (\(\text{S/m}\)) y faradios por metro (\(\text{F/m}\)), respectivamente. Los valores de\(R,\: L,\: G\), y\(C\) son afectados por la geometría de la línea de transmisión y por las propiedades eléctricas de los dieléctricos y conductores. \(C\)describe la capacidad de almacenar energía eléctrica y se debe principalmente a las propiedades del dieléctrico. \(G\)describe la pérdida en el dieléctrico que deriva de la conducción en el dieléctrico y de la relajación dieléctrica. La mayoría de los sustratos de microondas tienen una conductividad insignificante, por lo que domina la pérdida de relajación La pérdida de relajación dieléctrica es el resultado del movimiento de los centros de carga que resultan en la distorsión de la red dieléctrica (si es un cristal) o estructura molecular. La variación periódica del\(E\) campo transfiere energía del campo EM a vibraciones mecánicas. \(R\)se debe a la pérdida óhmica en el metal más que a cualquier otra cosa. \(L\)describe la capacidad de almacenar energía magnética y es principalmente una función de la geometría, ya que la mayoría de los materiales utilizados con las líneas de transmisión tienen\(\mu_{r} = 1\) (por lo que no se almacena más energía magnética que en un vacío).

Para la mayoría de las líneas los efectos se deben\(L\) y\(C\) dominan debido a la resistencia en serie relativamente baja y la conductancia de derivación. Las características de propagación de la línea se describen por su línea equivalente sin pérdidas, o sin pérdidas, aunque en la práctica alguna información sobre\(R\) o\(G\) es necesaria para determinar la potencia

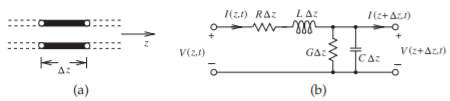
Figura\(\PageIndex{1}\): Segmento de línea de transmisión: (a) de longitud\(\Delta z\); y (b) modelo de elementos grumosos.

pérdidas. El concepto sin pérdidas es solo una aproximación útil y buena.

2.2.2 Derivación de Propiedades de Línea de Transmisión

En esta sección se derivan las ecuaciones diferenciales que rigen la propagación de señales en una línea de transmisión. Estas son ecuaciones diferenciales acopladas de primer orden y son similares a las ecuaciones de Maxwell en una dimensión. La solución de las ecuaciones diferenciales describe cómo se propagan las señales, y conduce a la extracción de algunos parámetros que describen las propiedades de la línea de transmisión.

Aplicando las leyes de Kirchoff aplicadas al modelo de la Figura\(\PageIndex{1}\) (b) y tomando el límite como\(\Delta z\to 0\) son las ecuaciones de línea de transmisión

\[\begin{align}\label{eq:1}\frac{\partial v(z,t)}{\partial z}&=-Ri(z,t)-L\frac{\partial i(z,t)}{\partial t} \\ \label{eq:2}\frac{\partial i(z,t)}{\partial z}&=-Gv(z,t)-C\frac{\partial v(z,t)}{\partial t}\end{align} \]

Nota

\(V(z)\)es un fasor y\(v(z, t) = \Re\{ V(z)e^{\jmath\omega t}\}\). \(\Re\{w\}\)denota la parte real de\(w\), un número complejo.

En estado estacionario sinusoidal usando fasores basados en coseno, estos se convierten en

\[\label{eq:3}\frac{dV(z)}{dz}=-(R+\jmath\omega L)I(z) \]

y

\[\label{eq:4}\frac{dI(z)}{dz}=-(G+\jmath\omega C)V(z) \]

Al eliminar\(I(z)\) en lo anterior se obtiene la ecuación de onda para\(V(z)\):

\[\label{eq:5}\frac{d^{2}V(z)}{dz^{2}}-\gamma^{2}V(z)=0 \]

Del mismo modo

\[\label{eq:6}\frac{d^{2}I(z)}{dz^{2}}-\gamma^{2}I(z)=0 \]

donde la constante de propagación es

\[\label{eq:7}\gamma =\alpha +\jmath\beta =\sqrt{(R+\jmath\omega L)(G+\jmath\omega C)} \]

con unidades SI de\(\text{m}^{−1}\) y donde\(\alpha\) es el coeficiente de atenuación y tiene unidades de nepers por metro (\(\text{Np/m}\)), y\(\beta\) es el coeficiente de cambio de fase, o constante de fase, y tiene unidades de radianes por metro (expresado como\(\text{rad/m}\) o radianes/m). Nepers y radianes son unidades adimensionales, pero sirven como indicaciones para lo que se refiere.

Ecuaciones\(\eqref{eq:5}\) y\(\eqref{eq:6}\) son ecuaciones diferenciales de segundo orden que tienen soluciones de la forma

\[\label{eq:8}V(z)=V_{0}^{+}e^{-\gamma z}+V_{0}^{-}e^{\gamma z} \]

y

\[\label{eq:9}I(z)=I_{0}^{+}e^{-\gamma z}+I_{0}^{-}e^{\gamma z} \]

La interpretación física de estas soluciones es que\(V^{+}(z) = V_{0}^{+}e^{−\gamma z}\) y\(I^{+}(z) = I_{0}^{+}e^{−\gamma z}\) son olas que viajan hacia adelante (moviéndose en la\(+z\) dirección) y\(V^{−}(z) = V_{0}^{−}e^{\gamma z}\) y\(I^{−}(z) = I_{0}^{−}e^{\gamma z}\) son ondas que viajan hacia atrás (moviéndose en la\(−z\) dirección). \(V(z),\: V_{0}^{+},\: V_{0}^{−},\: I(z),\: I_{0}^{+}\)y todos\(I_{0}^{−}\) son fasores. La ecuación de sustitución\(\eqref{eq:8}\) en la ecuación\(\eqref{eq:3}\) da como resultado

\[\label{eq:10}I(z)=\frac{\gamma}{R+\jmath\omega L}\left[ V_{0}^{+}e^{-\gamma z}-V_{0}^{-}e^{\gamma z}\right] \]

Luego de Ecuaciones\(\eqref{eq:10}\) y\(\eqref{eq:9}\)

\[\label{eq:11}I_{0}^{+}=\frac{\gamma}{R+\jmath\omega L}V_{0}^{+}\quad\text{and}\quad I_{0}^{-}=\frac{\gamma}{R+\jmath\omega L}(-V_{0}^{-}) \]

La impedancia característica se define como

\[\label{eq:12}Z_{0}=\frac{V_{0}^{+}}{I_{0}^{+}}=\frac{-V_{0}^{-}}{I_{0}^{-}}=\frac{R+\jmath\omega L}{\gamma}=\sqrt{\frac{R+\jmath\omega L}{G+\jmath\omega C}} \]

con la unidad SI de ohmios (\(\Omega\)). Ecuaciones\(\eqref{eq:8}\) y se\(\eqref{eq:9}\) pueden reescribir como

\[\label{eq:13}V(z)=V_{0}^{+}e^{-\gamma z}+V_{0}^{-}e^{\gamma z} \]

y

\[\label{eq:14}I(z)=\frac{V_{0}^{+}}{Z_{0}}e^{-\gamma z}-\frac{V_{0}^{-}}{Z_{0}}e^{\gamma z} \]

Conversión de nuevo al dominio de tiempo:

\[\label{eq:15} v(z,t)=|V_{0}^{+}|\cos(\omega t-\beta z+\varphi^{+})e^{-\alpha z}+|V_{0}^{-}|\cos(\omega t+\beta z+\varphi^{-})e^{\alpha z} \]

donde\(\varphi^{+}\) y\(\varphi^{-}\) son fases de las olas que viajan hacia adelante y hacia atrás, respectivamente. Los fasores de las ondas de voltaje circulantes son

\[\label{eq:16}V_{0}^{+}(z)=|V_{0}^{+}|e^{\jmath\varphi^{+}}e^{-\jmath\beta z}\quad\text{and}\quad V_{0}^{-}(z)=|V_{0}^{-}|e^{\jmath\varphi^{-}}e^{\jmath\beta z} \]

Se definen las siguientes cantidades:

\[\begin{align}\label{eq:17} \text{Characteristic impedance:} \quad&Z_{0}=\sqrt{(R+\jmath\omega L)/(G+\jmath\omega C)} \\ \label{eq:18}\text{Propagation constant:} \quad&\gamma =\sqrt{(R+\jmath\omega L)/(G+\jmath\omega C)} \\ \label{eq:19} \text{Attenuation constant:} \quad&\alpha =\Re\{\gamma\} \\ \label{eq:20}\text{Phase constant:} \quad&\beta=\Im\{\gamma\} \\ \label{eq:21}\text{Wavenumber:} \quad& k=-\jmath\gamma \\ \label{eq:22}\text{Phase velocity:}\quad&v_{p}=\omega/\beta \\ \label{eq:23}\text{Wavelenght:}\quad&\lambda=\frac{2\pi}{|\gamma|}=\frac{2\pi}{|k|}\end{align} \]

donde\(\omega = 2\pi f\) es la frecuencia de radianes y\(f\) es la frecuencia con las unidades SI de hertz (\(\text{Hz}\)). El número de onda tal\(k\) como se define aquí se usa en electromagnetismo y en lo que respecta a la propagación de ondas. Considerando una de las ondas viajeras, la velocidad de fase se refiere a la velocidad aparente de la cual un punto de fase constante en la onda sinusoidal parece moverse.

Para materiales de baja pérdida\(\alpha ≪\beta\), y así\(\beta ≈ |k|\), entonces las siguientes aproximaciones son válidas:

\[\begin{align}\label{eq:24}\text{Characteristic impedance:}\quad&Z_{0}\approx\sqrt{L/C} \\ \label{eq:25}\text{Phase constant:}\quad&\beta\approx\omega\sqrt{LC} \\ \label{eq:26}\text{Wavenumber:}\quad&k\approx\beta \\ \label{eq:27}\text{Phase velocity:}\quad&v_{p}=\omega/\beta \\ \label{eq:28}\text{Wavelength:}\quad&\lambda\approx\frac{2\pi}{\beta}=v_{p}/f\end{align} \]

El resultado importante aquí es que se puede definir una onda de voltaje (y una onda de corriente) en una línea de transmisión. Se necesita introducir un parámetro más: la velocidad del grupo,

\[\label{eq:29}v_{g}=\frac{\partial\omega}{\partial\beta} \]

La velocidad de grupo es la velocidad de la envolvente de una forma de onda modulada y describe qué tan rápido se propaga la información. Es la velocidad a la que se mueve la energía (es decir, la información) en la forma de onda. Así la velocidad del grupo nunca puede ser mayor que la velocidad de la luz en un vacío,\(c\). Velocidad de fase, sin embargo, puede ser más de\(c\). Si la velocidad a la que se mueve la información varía con la frecuencia, entonces una señal como un pulso se extenderá. Se dice que tal línea tiene dispersión. Para una línea sin pérdidas, sin dispersión, la velocidad de grupo y fase son las mismas. Si la velocidad de fase es independiente de la frecuencia, entonces\(\beta\) es linealmente proporcional a\(\omega\).

La longitud eléctrica se utiliza en diseños con líneas de transmisión antes de establecer la longitud física de la línea. La longitud eléctrica de una línea se expresa ya sea como una fracción de una longitud de onda o en grados (o radianes), donde una longitud de onda corresponde a\(360^{\circ}\) (o\(2π\) radianes). Entonces si\(\beta\) es la constante de fase de una señal en la línea y\(ell\) es su longitud física, la longitud eléctrica de la línea en radianes es\(\beta\ell\).

Ejemplo\(\PageIndex{1}\): Physical and Electrical Length

Una línea de transmisión es\(10\text{ cm}\) larga y a la frecuencia de operación la constante de fase\(\beta\) es\(30\text{ rad/m}\). ¿Cuál es la longitud eléctrica de la línea?

Solución

La longitud física de la línea es\(\ell = 10\text{ cm} = 0.1\text{ m}\). Entonces la longitud eléctrica de la línea es\(\ell_{e} = \beta\ell = (30\text{ rad/m})\times 0.1\text{ m} = 3\text{ radians}\). La longitud eléctrica también se puede expresar en términos de longitud de onda señalando que\(360^{\circ}\) corresponde a\(2π\) radianes, que también corresponde a\(\lambda\). Así\(\ell_{e} = (3\text{ radians})=3\times 360/(2π) = 171.9^{\circ}\) o\(\ell_{e} = 3/(2π)\lambda = 0.477\lambda\).

Ejemplo\(\PageIndex{2}\): \(RLGC\) Parameters

Una línea de transmisión tiene los\(RLGC\) parámetros\(R = 100\: Ω\text{/m},\: L = 80\text{ nH/m},\: G = 1.6\text{ S/m}\), y\(C = 200\text{ pF/m}\). Considera una ola viajera\(2\text{ GHz}\) en la línea.

1. ¿Cuál es la constante de atenuación?
2. ¿Cuál es la constante de fase?
3. ¿Cuál es la velocidad de fase?
4. ¿Cuál es la impedancia característica de la línea?
5. ¿Cuál es la velocidad del grupo?

Solución

1. \(\alpha:\:\gamma =\alpha +\jmath\beta = \sqrt{(R + \jmath\omega L) (G +\jmath\omega C)};\:\quad\omega = 12.57\cdot 10^{9}\text{ rad/s}\)
   \[\begin{aligned}\gamma&=\sqrt{(100 +\jmath\omega\cdot 80\cdot 10^{−9}) (1.6 +\jmath\omega 200\times 10^{−12})}=(17.94 + \jmath 51.85)\text{ m}^{−1} \\ \alpha&=\Re\{\gamma\}=17.94\text{ Np/m}\nonumber\end{aligned} \nonumber \]
2. Constante de fase:
   \[\beta = \Im\{\gamma\} = 51.85\text{ rad/m}\nonumber \]
3. Velocidad de fase”
   \[v_{p}=\frac{\omega}{\beta}=\frac{2\pi f}{\beta}=\frac{12.57\times 10^{9}\text{ rad}\cdot\text{s}^{-1}}{51.85\text{ rad}\cdot\text{m}^{-1}}=2.42\times 10^{8}\text{ m/s}\nonumber \]
4. \(Z_{0} = (R +\jmath\omega L)/\gamma = (100 + \jmath\omega\cdot 80\cdot 10^{−9})/(17.94 + \jmath 51.85) = (17.9 + \jmath 4.3)\:\Omega\)
   Tenga en cuenta también eso\(Z_{0} = \sqrt{(R + \jmath\omega L)/(G + \jmath\omega C)}\), lo que arroja la misma respuesta.
5. Velocidad de grupo: Se utilizarán derivados
   \[v_{g}=\left.\frac{\partial\omega}{\partial\beta}\right|_{f=2\text{ GHz}}\nonumber \]
   numéricos, así\(v_{g} = \Delta\omega/\Delta\beta\). Ahora ya\(\beta\) se conoce en\(2\text{ GHz}\). En\(1.9\text{ GHz}\),\(\gamma = 17.884 + \jmath 49.397\text{ m}^{−1}\), y así\(\beta = 49.397\text{ rad/m}\).
   \[v_{g}=\frac{2π(2\text{ GHz} − 1.9\text{ GHz})}{\beta(2\text{ GHz}) − \beta(1.9\text{ GHz})}=\frac{2π(2 − 1.9)10^{9}\text{ Hz}}{(51.85 − 49.397)\text{ m}^{−1}}=2.563\times 10^{8}\text{ m/s}\nonumber \]
   (Tenga en cuenta que\(\text{Hz} = \text{s}^{−1}\). Tenga en cuenta que\(v_{g}\neq v_{p}\), y así la línea de transmisión tiene dispersión.)

2.2.3 Relación de los parámetros de RLGC con la permitividad y permeabilidad de un medio

En la sección anterior se derivaron las ecuaciones del telégrafo para una línea de transmisión modelada como subsecciones de\(RLGC\) elementos. Se obtiene una precisión muy buena si la longitud de una subsección no supera la vigésima parte de una longitud de onda. El modelo de línea de transmisión completa es la cascada de muchas subsecciones de línea de transmisión (por ejemplo, ver Figura\(\PageIndex{2}\)). En esta sección los\(RLGC\) parámetros están relacionados con los parámetros físicos de permitividad y permeabilidad. El desarrollo no entra en muchos detalles, ya que la derivación está involucrada y solo se puede derivar analíticamente para unas pocas estructuras de líneas de transmisión regulares. Si tienes curiosidad, el desarrollo se realiza para una guía de ondas de placa paralela y una guía de ondas rectangular en el Capítulo 6 y para una línea coaxial en la Sección 2.9.

Los principales parámetros que describen la propagación en una línea de transmisión son\(Z_{0}\) y\(\gamma\), y estos dependen de la permeabilidad y permitividad del medio y la variación espacial de los\(H\) campos\(E\) y resultantes de la geometría de los conductores. Solo unas pocas geometrías permiten la solución analítica de los campos por lo que en general se requiere\(Z_{0}\) y\(\gamma\) deriva una solución de campo numérico. Muy a menudo las ecuaciones son curvas ajustadas a las soluciones numéricas pero la estructura de las ecuaciones tiene una base teórica. Se encuentra que puede haber una serie de posibles soluciones de campo (no inusuales para la solución de ecuaciones diferenciales) cada una de las cuales se llama modo. Los modos que tienen todos los campos en el plano transversal (perpendicular a la dirección de propagación) se denomina modo EM transversal (TEM) y estos modos existen en DC. Los otros modos solo son posibles por encima de una frecuencia de corte. Se encuentra que la constante de propagación tiene la forma

\[\label{eq:30}\gamma^{2}=-(k^{2}-k_{c}^{2}) \]

donde\(k_{c}\) es el número de onda de corte y para una línea en particular generalmente tiene un valor diferente para cada modo. El número de onda de una línea homogénea es

\[\label{eq:31}k=\jmath\omega\sqrt{\mu\varepsilon} \]

Un modo solo puede existir y describir una señal de propagación cuando no\(\beta = \Im\{\gamma\}\) es cero lo que requiere que\(\gamma^{2}\) sea negativo. Por lo tanto, un modo puede soportar un modo de propagación solo si el número de onda es mayor que el número de onda de corte, es decir, cuándo\(k>k_{c}\). Un modo TEM tiene\(k_{c} = 0\) así una señal, que no sea DC siempre se puede propagar en la línea en un modo TEM. Una línea homogénea tiene solo un tipo de medio que soporta los campos EM. Un ejemplo de una línea homogénea es una línea coaxial rellena de teflón. Una línea no homogénea tiene dos o más medios dieléctricos, como el aire y un dieléctrico. Para líneas no homogéneas se utiliza el concepto de una línea homogénea equivalente con una permitividad efectiva\(\varepsilon_{\text{eff}}\) y permeabilidad\(\mu_{\text{eff}}\) efectiva. Entonces

\[\label{eq:32}k=\jmath\omega\sqrt{\mu_{\text{eff}}\varepsilon_{\text{eff}}} \]

Figura\(\PageIndex{2}\):\(RLGC\) modelo de una línea de transmisión.

La pérdida se incorpora en las partes imaginarias de\(\varepsilon\) y\(\mu\) para los modos TEM. Como antes, para cualquier modo,

\[\begin{align}\label{eq:33}\text{Attenuation constant:}\quad&\alpha=\Re\{\gamma\} \\ \label{eq:34}\text{Phase constant:}\quad&\beta=\Im\{\gamma\} \\ \label{eq:35}\text{Phase velocity:}\quad&v_{p}=\omega/\beta \\ \label{eq:36}\text{Wavelength:}\quad&\lambda=\frac{v_{p}}{f}=\frac{2\pi}{\beta}\end{align} \]

Comparando\(\gamma\) en Ecuaciones\(\eqref{eq:7}\) y\(\eqref{eq:32}\), se puede desarrollar una equivalencia entre la forma de elemento grumado de propagación de línea de transmisión y la propagación de una onda EM en un medio. Específicamente,

\[\label{eq:37}-\omega^{2}\mu_{\text{eff}}\varepsilon_{\text{eff}}=(R+\jmath\omega L)(G+\jmath\omega C) \]

Medio sin pérdidas

Si el medio es sin pérdidas (\(\mu\)y\(\varepsilon\) son reales y\(R =0= G\)), entonces

\[\label{eq:38}\mu_{\text{eff}}\varepsilon_{\text{eff}}=LC \]

Cuando el medio es espacio libre (un vacío), entonces se usa un subíndice cero. El espacio libre también es sin pérdidas, por lo que los siguientes resultados se mantienen:

\[\label{eq:39}\alpha_{0}=0\quad\text{and}\quad\beta_{0}=-\jmath\gamma=\omega\sqrt{\mu_{0}\varepsilon_{0}}=\omega\sqrt{LC} \]

Si la frecuencia se especifica en gigahercios (indicado por\(f_{\text{GHz}}\)), en espacio libre

\[\label{eq:40}\beta_{0}=20.958\:f_{\text{GHz}}\quad\text{units of rads/m} \]

At\(1\text{ GHz}\),\(\beta_{0} = 20.958\text{ rad/m}\) y\(\lambda_{0} = 29.98\text{ cm}\) (usar\(\lambda_{0}\approx 30\text{ cm}\) at\(1\text{ GHz}\) como referencia). En un medio sin pérdidas con permeabilidad relativa efectiva\(\mu_{e} = \mu_{\text{eff}}/\mu_{0} = 1\) y permitividad relativa efectiva\(\varepsilon_{e} = \varepsilon_{\text{eff}}/\varepsilon_{0}\),

\[\label{eq:41}\beta=\sqrt{\varepsilon_{e}}\beta_{0} \]

\(Z_{0}\)depende fuertemente de la variación espacial de los campos. Cuando no hay variación en el plano transversal a la dirección de propagación (es decir, para la propagación de ondas planas)

\[\label{eq:42}Z_{0}=\sqrt{\mu/\varepsilon} \]

Sin embargo, si hay variación de los campos

\[\label{eq:43}Z_{0}=\kappa\sqrt{\mu_{\text{eff}}/\varepsilon_{\text{eff}}}=\kappa\sqrt{\mu_{0}/\varepsilon_{0}}\sqrt{\mu_{e}/\varepsilon_{e}} \]

donde\(\kappa\) captura el efecto de variación geométrica de los campos. La variación espacial de los campos almacena energía adicional en los\(H\) campos\(E\) y, afectando así\(\gamma\) como\(Z_{0}\).

Si las condiciones de límite en una línea de transmisión son tales que no se puede soportar una variación espacial requerida de los campos, entonces la señal no puede propagarse. La frecuencia crítica a la que\(k =\jmath\omega\sqrt{\mu\varepsilon} = k_{c}\) se llama la frecuencia de corte,\(f_{c}\). Las señales no pueden propagarse en la línea si la frecuencia está por debajo\(f_{c}\). Para el resto de este capítulo las únicas líneas consideradas son aquellas para las cuales\(k_{c} = 0\), (y\(f_{c} = 0\)), es decir modos TEM en líneas de transmisión. Es decir, las líneas llevan señales de CC.

Media de baja pérdida

La pérdida de línea de transmisión se debe a la resistencia de los conductores, que se describe por\(R\), y la pérdida en el dieléctrico descrito por\(G\). Para la mayoría de los dieléctricos hay muy poca pérdida conductora y la pérdida se debe casi en su totalidad a la relajación dieléctrica. (La excepción más común es cuando el dieléctrico es silicio ya que puede haber una conducción apreciable en el silicio). En la relajación dieléctrica un campo eléctrico hace que los centros de carga se muevan y estos provocan que vibre la celosía que sabemos que es calor por lo que la energía se transfiere del campo eléctrico al calor. La energía perdida es proporcional a la frecuencia y por lo tanto\(G\) es directamente proporcional a la frecuencia y en consecuencia, siempre que no haya conducción en el dieléctrico, la tangente de pérdida de la línea de transmisión se define así como:

\[\label{eq:44}\tan\delta =G\omega C=\text{ independent of frequency} \]

Una consecuencia de la Ecuación\(\eqref{eq:44}\), y señalando que\(C\) es aproximadamente independiente de la frecuencia,\(G\) es que si se conoce a una frecuencia entonces su valor a otra frecuencia puede determinarse rápidamente.

La tangente de pérdida del medio dieléctrico y la tangente de pérdida de la línea de transmisión pueden no ser las mismas ya que los campos EM pueden no estar confinados solo al medio, por ejemplo, los campos están en el aire y en un dieléctrico.

2.2.4 Dimensiones de\(\gamma,\:\alpha,\) y\(\beta\)

La unidad SI de\(\gamma\) son metros inversos (\(\text{m}^{−1}\)) y la constante de atenuación,\(\alpha\), y la constante de fase\(\beta\),, tienen, estrictamente hablando, las mismas unidades. Sin embargo, la convención es introducir las cantidades adimensionales Néper y radián para transmitir información adicional. Así la constante de atenuación\(\alpha\) tiene las unidades de Nepers por metro (\(\text{Np/m}\)) y la constante de fase\(\beta\) tiene las unidades radianes por metro (\(\text{rad/m}\)). La unidad Néper proviene del nombre del\(\text{e} (= 2.7182818284590452354...)\) símbolo (escrito en fuente vertical y no en cursiva ya que es una constante), que se llama el Neper. El Néper se utiliza en el cálculo de niveles de señal de línea de transmisión, como en Ecuaciones\(\eqref{eq:8}\) y\(\eqref{eq:9}\). Las constantes de atenuación y fase a menudo se separan y luego la constante de atenuación describe la disminución en la amplitud de la señal a medida que la señal viaja por una línea de transmisión. Entonces\(\alpha\ell = 1\text{ Np}\), cuando, dónde\(\ell\) está la longitud de la línea, la señal ha disminuido a\(1/\text{e}\) de su valor original, y la potencia cae a\(1/\text{e}^{2}\) de su valor original. La disminución en el nivel de señal representa pérdida y se utilizan con las unidades de decibelios por metro (\(\text{dB/m}\))\(1\text{ Np} = 20 \log \text{e} = 8.6858896381\text{ dB}\). Entonces expresando\(\alpha\) como\(1\text{ Np/m}\) es lo mismo que decir que la pérdida de atenuación es\(8.6859\text{ dB/m}\). Convertir de\(\text{dB}\) a\(\text{Np}\) multiplicar por\(0.1151\). Así\(\alpha = x\text{ dB/m} = x\times 0.1151\text{ Np/m}\).

Nota

El nombre para e deriva de John Napier, quien desarrolló la teoría de logaritmos [3]. \(\text{e}\)a veces se llama constante de Euler.

Nota

En ingeniería\(\log x ≡ \log_{10} x\) y\(\ln x ≡ \log_{e} x\).

Ejemplo\(\PageIndex{3}\): Transmission Line Characteristics

Una línea tiene una atenuación de\(10\text{ dB/m}\) y una constante de fase de\(50\text{ radians/m}\) at\(2\text{ GHz}\).

1. ¿Cuál es la constante de propagación compleja de la línea de transmisión?
2. Si la capacitancia de la línea es\(100\text{ pF/m}\) y la pérdida conductora es cero (es decir,\(G = 0\)), ¿cuál es la impedancia característica de la línea?

Solución

1. \(\alpha|_{\text{Np}} = 0.1151\times \alpha|_{\text{dB}} = 0.1151\times (10\text{ dB/m}) = 1.151\text{ Np/m},\:\beta = 50\text{ rad/m}\)
   Constante de propagación,\(\gamma =\alpha +\jmath\beta = (1.151 + \jmath 50)\text{ m}^{−1}\)
2. \(\gamma =\sqrt{(R +\jmath\omega L) (G +\jmath\omega C)}\), y\(Z_{0} = \sqrt{(R +\jmath\omega L)/(G +\jmath\omega C)}\),
   por lo tanto\(Z_{0} = \gamma /(G + \jmath\omega C)\)\(\omega = 2π\cdot 2\times 10^{9}\text{ s}^{−1}\);\(G = 0\);;\(C = 100 \times 10^{−12}\text{ F}\), entonces\(Z_{0} = 39.8 −\jmath 0.916\:\Omega\).

2.2.5 Línea de transmisión sin pérdidas

Si el conductor y el dieléctrico son ideales (es decir, sin pérdidas), entonces\(R =0= G\) y las ecuaciones para las características de la línea de transmisión simplifican. Los parámetros de la línea de transmisión de Ecuaciones\(\eqref{eq:12}\) y\(\eqref{eq:18}\) —\(\eqref{eq:23}\) son entonces

\[\begin{align}\label{eq:45}Z_{0}&=\sqrt{\frac{L}{C}} \\ \label{eq:46}\beta&=\omega\sqrt{LC} \\ \label{eq:47}\lambda_{g}&=\frac{2\pi}{\omega\sqrt{LC}}=\frac{v_{p}}{f} \\ \label{eq:48}\alpha&=0 \\ \label{eq:49}v_{p}&=1/\sqrt{LC}\end{align} \]

Tenga en cuenta que existe una distinción entre una línea de transmisión y un circuito RLC. Cuando se hace referencia a una línea de transmisión como que tiene una impedancia de\(50\:\Omega\), esto se refiere a la línea que tiene una impedancia característica de\(50\:\Omega\), la línea no puede ser reemplazada por una\(50\:\Omega\) resistencia.

Una línea no puede ser reemplazada por un elemento agrupado excepto en lo siguiente:

1. Al calcular la onda de voltaje directo de una línea que es infinitamente larga (o no hay reflejos de la carga). Entonces la línea puede ser reemplazada por una impedancia igual a la impedancia característica de la línea. El voltaje total es entonces solo el componente que viaja hacia adelante.
2. La impedancia característica y la impedancia de carga se utilizan para calcular la impedancia de entrada de la línea terminada a una frecuencia particular.

2.2.6 Línea Coaxial

El cálculo analítico de la impedancia característica de una línea de transmisión a partir de la geometría no siempre es posible excepto por algunas geometrías regulares (sistemas de coordenadas ortogonales coincidentes). Para una línea coaxial, los campos eléctricos se extienden en una dirección radial desde el conductor central hasta el conductor externo. Por lo que es posible calcular el voltaje integrando este\(E\) campo desde el centro hacia el conductor externo. El campo magnético es circular, centrado en el conductor central, por lo que la corriente en el conductor se puede calcular como la integral cerrada del campo magnético. (Aquí las líneas de campo y los límites del conductor corresponden al sistema de coordenadas cilíndricas). Resolviendo para los campos en la región entre los conductores central y exterior produce la siguiente fórmula para la impedancia característica de una línea coaxial (la derivación se presenta en la Sección 2.9):

\[\label{eq:50}Z_{0}=138\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\log\left(\frac{b}{a}\right)\:\Omega =60\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left(\frac{b}{a}\right)\:\Omega \]

donde\(\varepsilon_{r}\) es la permitividad relativa del medio entre los conductores central y exterior,\(b\) es el diámetro interno del conductor externo, y\(a\) es el diámetro exterior del conductor interno. Con una mayor\(\varepsilon\), más energía se almacena en el campo eléctrico y la capacitancia por unidad de longitud de la línea,\(C\), aumenta. A medida que aumenta la permitividad relativa de la línea, la impedancia característica de la línea se reduce. \(\eqref{eq:50}\)La ecuación es una formulación exacta para la impedancia característica de una línea coaxial. Tal fórmula sólo puede aproximarse para casi todas las demás líneas.

La mayoría\(Z_{0}\) de los cables coaxiales tienen de\(50\:\Omega\), pero diferentes relaciones de b y a producen propiedades especiales de la línea coaxial. Cuando la relación es\(1.65\) para una línea llena de aire,\(Z_{0} = 30\:\Omega\) y la línea tiene la capacidad máxima de transporte de energía. El

Figura\(\PageIndex{3}\): Adaptadores de línea coaxial: (a) tipo N hembra a hembra (N (f) a N (f)); (b) APC-7 a tipo N macho (APC-7-a-N (m)); (c) APC-7 a macho tipo SMA (APC-7 a SMA (m)); adaptadores SMA: (d) tipo SMA hembra (SMA (f) a SMA (f)); e) de tipo SMA macho a hembra (SMA (m) -TOSMA (f)); (f) de tipo SMA macho a macho ( SMA (m) a SMA (m)); y (g) codo SMA. N, APC-7 y SMA se conocen como serie de conectores.

para la ruptura de voltaje máximo es\(2.7\), correspondiente a\(Z_{0} = 60\:\Omega\) para una línea llena de aire. La impedancia característica para la atenuación mínima en una línea llena de aire es\(77\:\Omega\), con una relación de diámetro de\(3.59\). Esta relación óptima de conductores externos a internos para una pérdida mínima es independiente del dieléctrico y los dieléctricos típicos tienen una pérdida insignificante con pérdida de línea debida casi en su totalidad a los conductores. Si el dieléctrico que llena la línea coaxial es polietileno (que es el más común) con\(\varepsilon_{r} = 2.3\), la impedancia característica de la línea de pérdida mínima es\(50.6\:\Omega\).

La velocidad de propagación en una línea coaxial sin pérdidas que tiene un medio uniforme es la misma que para una onda plana en el medio, es decir\(v_{g} = c/\sqrt{\varepsilon_{r}}\). Hay una salvedad. Esto es cierto para todas las estructuras de líneas de transmisión que soportan la variación mínima de los campos correspondientes a un modo TEM. Los modos de orden superior, con mayores variaciones espaciales de los campos viajarán más lentamente (es decir\(v_{g} < c/\sqrt{\varepsilon_{r}}\)), serán considerados en el Capítulo 4. El diámetro del conductor externo y el tipo de soportes internos para el conductor interno determinan el rango de frecuencia de los componentes coaxiales. A frecuencias altas y, por lo tanto, longitudes de onda cortas, las grandes dimensiones internas de un cable de gran diámetro pueden soportar más de una variación espacial de los campos EM, es decir, más de un modo. Esto no es deseable porque dos modos viajarán a diferentes velocidades y una señal de propagación divide la energía entre los dos modos y, dado que los modos tienen diferentes velocidades de grupo, la señal se volverá confusa. Así, las dimensiones transversales del cable determinan su límite de frecuencia superior para una transmisión confiable de la señal.

Existen diversas líneas coaxiales con diferentes diámetros y diferentes niveles de atención dada a la uniformidad de las líneas. Cada tipo de línea se llama serie y es necesario convertir entre series usando adaptadores. Varios adaptadores se muestran en la Figura\(\PageIndex{3}\). Principalmente estos tienen diferente costo, pérdida, y uniformidad de\(Z_{0}\). A menudo es necesario convertir entre series y también convertir entre los sexos (macho y hembra) de conectores. Tenga en cuenta que un enchufe (o jack) puede ser hembra o macho.

La diferente construcción de los conectores se puede ver en la Figura\(\PageIndex{4}\). Con el conector APC-7 mostrado en la Figura\(\PageIndex{4}\) (a) el diámetro interior del conductor externo es\(7\text{ mm}\). La característica única de este conector es que es asexuado, con la placa de interfaz cargada por resorte. Es decir, un conector APC-7 siempre se puede conectar a otro conector APC-7. Estos son de precisión

Figura\(\PageIndex{4}\): Varios conectores coaxiales de línea de\(50\:\Omega\) transmisión: (a) conector coaxial APC-7 (diámetro del conductor\(7\text{ mm}\) externo); (b) conector coaxial hembra tipo N (N (f)\(7\text{ mm}\)) (); (c) conector coaxial tipo SMA macho (SMA (m)) (\(3.5\text{ mm}\)); (d) CC a\(26\text{ GHz}\), precisión SMA de 2 W fijos atenuador; y (e) filtro de\(500\text{ MHz}\) paso bajo en línea de tipo N. (d) y (e) copyright 2012 Scientific Components Corporation d/b/a Mini-Circuitos, utilizados con permiso [4]).

Figura\(\PageIndex{5}\): Líneas coaxiales: (a) cables SMA (desde la parte superior): cable flexible tipo I, tipo II, tipo III y cable semirrígido; (b) cables coaxiales que muestran capas; (c) doblador de cable coaxial semirrígido; (d) doblador con línea; y (e) cable formable a mano que soporta radio estrecho con bajo retorno y pérdida de inserción. (b) Copyright Megaphase LLC, utilizado con permiso [5].) (e) Copyright 2012 Scientific Components Corporation d/b/a Mini-Circuitos, utilizados con permiso [4].)

conectores utilizados en algunas mediciones de microondas. El conector de tipo N en la Figura\(\PageIndex{4}\) (b) y el conector SMA en la Figura\(\PageIndex{4}\) (c) son conectores más comunes del día a día. En las Figuras\(\PageIndex{4}\) (d y e) se muestran diferentes vistas de estos conectores. A diferencia de un conector APC-7, un conector macho de tipo N (o SMA), por ejemplo, solo se puede conectar a un conector hembra de tipo N. Hay una gran cantidad de diferentes tipos o series de conectores para aplicaciones de alta potencia, diferentes rangos de frecuencia, niveles de distorsión y costo.

También hay muchos tipos de cables coaxiales, como se muestra en la Figura\(\PageIndex{5}\) (a). Estos son cables con conectores SMA (con diámetro de conductor\(3.5\text{ mm}\) externo). Los cables de microondas sin conectores se muestran en la Figura\(\PageIndex{5}\) (b). Estos cables varían en costo, flexibilidad y la cantidad de veces que pueden flexionarse o doblarse de manera confiable. El cable semirrígido que se muestra en la parte inferior de la Figura\(\PageIndex{5}\) (a) debe doblarse utilizando una herramienta de doblado, como se muestra en la Figura\(\PageIndex{5}\) (c), y en

Figura\(\PageIndex{6}\): Llave dinamométrica utilizada en la realización de conexiones coaxiales repetibles. Copyright MegaPhase LLC, usado con permiso [5].

utilizar en la Figura\(\PageIndex{5}\) (d). El radio de curvatura controlado garantiza un cambio mínimo en la impedancia característica y la constante de propagación del cable. Sin embargo, los cables semirrígidos solo pueden doblarse una vez. La curva de mayor precisión se realiza utilizando una curva acodada, que se muestra en la Figura\(\PageIndex{3}\) (g). Varios cables flexibles tienen diferentes respuestas a la flexión, con cables de mayor precisión (y más caros) que tienen el menor impacto en la impedancia característica y las variaciones de fase a medida que los cables se flexionan.

Las mediciones de precisión requieren que los conectores se conecten de manera repetible con una llave dinamométrica, como se muestra en la\(\PageIndex{6}\) Figura Una llave dinamométrica se puede usar de manera convencional, pero una vez que se obtiene el par prescrito, la llave se rompe justo por encima de la cabeza. Esto asegura que dos conectores se unan de manera repetible con la misma fuerza y así la resistencia de contacto y la calidad de la conexión sea repetible.

2.2.7 Línea Microstrip

En la Figura\(\PageIndex{7}\) (a) se muestra una línea de microcinta. Esta es una línea de transmisión de uso común, ya que puede fabricarse a bajo costo utilizando técnicas de placa de circuito impreso. Esta línea consiste en un sustrato con respaldo metálico de permitividad relativa\(\varepsilon_{r}\) sobre el cual se encuentra una tira metálica. Por encima de eso está el aire. El ancho de la tira determina la impedancia característica de la línea. La impedancia característica de las líneas de microcinta que tienen varios anchos de banda se muestra en la Figura\(\PageIndex{8}\) para varias permitividades de sustrato. Entonces, cuanto más ancha es la tira y mayor es la permitividad del sustrato, menor es la impedancia característica de la línea. Los campos EM están parcialmente en el aire y en parte en el dieléctrico y se debe utilizar una permitividad efectiva al calcular la longitud eléctrica de la línea. Los resultados de simulaciones de campo de la permitividad efectiva de líneas de diversos anchos y con diversas permitividades de sustrato se muestran en la Figura\(\PageIndex{9}\), donde se puede observar que la permitividad relativa efectiva,\(\varepsilon_{e}\), aumenta para tiras anchas. Esto se debe a que más del campo EM está en el sustrato. Las estructuras de líneas de transmisión de microcinta a menudo se dibujan mostrando solo el diseño de la tira, como se muestra en la Figura\(\PageIndex{7}\) (b), donde

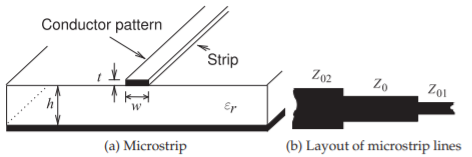
Figura\(\PageIndex{7}\): Línea de transmisión Microstrip. La vista de diseño (o superior) se usa comúnmente con diseños de circuitos que utilizan microcinta. Este es el patrón de la tira donde (b) muestra tres líneas de diferente anchura.

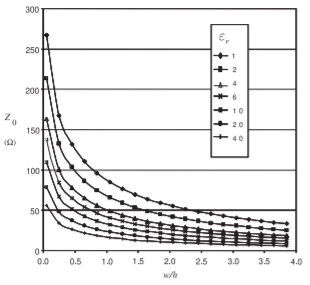
Figura\(\PageIndex{8}\): Dependencia\(Z_{0}\) de una línea de microcinta\(1\text{ GHz}\) para varias relaciones\(\varepsilon_{r}\) y aspecto (\(w/h\)). Calculado mediante simulación EM.

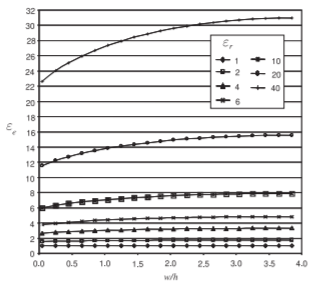
Figura\(\PageIndex{9}\): Dependencia de la permitividad relativa efectiva\(\varepsilon_{e}\) de una línea de microcinta\(1\text{ GHz}\) para diversas permitividades y relaciones de aspecto (\(w/h\)).

las tres líneas tienen diferentes impedancias características. El siguiente capítulo presenta análisis detallados de microcinta y otras líneas de transmisión planas.

2.2.8 Resumen

La conclusión importante de esta sección es que una señal se mueve en una línea de transmisión como ondas que viajan hacia adelante y hacia atrás. La energía transferida está en las olas viajeras. El voltaje y la corriente totales en un punto de la línea es la suma de las ondas de voltaje de desplazamiento y de corriente de desplazamiento, respectivamente, pero la vista de voltaje/corriente total no es suficiente para describir cómo funciona una línea de transmisión. La teoría de la línea de transmisión se expresa en términos de voltaje de desplazamiento y ondas de corriente y estas son similares a una forma unidimensional de las ecuaciones de Maxwell. Se desarrolló un argumento que postula un modelo de una línea como secciones en cascada del circuito RLGC y estos elementos de circuito pueden estar vagamente relacionados con las propiedades materiales del medio en el que está incrustada la línea de transmisión. Existen factores de modificación debido a la orientación real de los campos eléctrico y magnético y su desarrollo requiere un análisis detallado de campo de la geometría real de la línea de transmisión. Esto se puede hacer para una línea coaxial pero una línea de microcinta requiere análisis numérico.