2.9: Línea Coaxial

En esta sección se calcula la impedancia característica de una línea coaxial. La técnica supone que los campos dinámicos eléctricos y magnéticos serán los mismos que serían a CC. Esta visión física permite que el problema se resuelva de manera relativamente simple usando las leyes de campo estáticas. Posteriormente se considera la situación dinámica cuando se consideran los campos en una línea coaxial realista.

2.9.1 Impedancia característica de una línea coaxial

A continuación se obtienen los parámetros de longitud por unidad—\(R,\: L,\: G,\) y\(C\) —de una línea coaxial. De estos se deriva la impedancia característica y la constante de propagación de la línea coaxial. El desarrollo es un ejemplo de cómo se pueden desarrollar estos parámetros para cualquier línea de transmisión. La clave es utilizar un sistema de coordenadas que coincida con la estructura que se está considerando. Entonces las ecuaciones de Maxwell se pueden expresar de manera muy simple, generalmente como ecuaciones diferenciales ordinarias unidimensionales. Muy a menudo se pueden utilizar las leyes de campo eléctrico y magnético estático que simplifican aún más el desarrollo. Si un sistema de coordenadas ortogonales no coincide con las dimensiones de la línea, entonces a veces es posible utilizar una técnica matemática llamada mapeo conforme para mapear una forma no conforme, como una línea de microcinta, en una forma que coincida con un sistema de coordenadas ortogonales [20]. Una vez que se derivan los parámetros de la línea de transmisión, el resultado se asigna de nuevo a la estructura original. Afortunadamente, la mayoría de las estructuras de líneas de transmisión se ajustan a un sistema de coordenadas

La sección transversal de una línea coaxial se muestra en la Figura\(\PageIndex{1}\) (a) y tiene dos conductores concéntricos con el conductor interno que tiene un radio exterior de\(a\) y el interior del conductor externo con un radio\(b\). Los campos entre los conductores se pueden resolver expresando las relaciones de campo en coordenadas cilíndricas. A continuación se presenta una simplificación del tratamiento en [21], que se puede aplicar a una gama más amplia de cables coaxiales que solo el cable coaxial convencional simétrico circularmente en la Figura\(\PageIndex{1}\). La distribución de campo más simple posible se muestra en la Figura\(\PageIndex{1}\) (b). El primer parámetro a desarrollar es\(C\). Para ello, la carga en uno de los conductores está relacionada con el voltaje entre los conductores. Considere una sección de línea de longitud\(\Delta z\), luego usando la ley de Gauss, Ecuación (1.6.6), el flujo eléctrico se relaciona con la carga total encerrada. Así que en el radio\(r\),

\[\begin{align} \oint_{s}\overline{D}&=Q_{\text{enclosed}}\nonumber \\ \label{eq:1} 2\pi rD_{r}(r)\Delta z&=\rho_{\ell}\Delta z\quad\text{and}\quad 2\pi r\varepsilon E_{r}(r)\Delta z=\rho_{\ell}\varepsilon\Delta z\end{align} \]

donde\(\rho_{\ell}\) es la carga en el conductor interno por unidad de longitud (en la\(z\) dirección). Entonces el campo eléctrico radial es

\[\label{eq:2}\overline{E}=E_{r}(r)\hat{\mathbf{r}}=\frac{\rho_{\ell}}{2\pi r\varepsilon}\hat{\mathbf{r}} \]

y\(\mathbf{r}\) es el vector unitario en la dirección radial. El voltaje entre los conductores es

\[\label{eq:3}V=\int_{a}^{b}E_{r}\cdot dr=\int_{a}^{b}\frac{\rho_{\ell}}{2\pi r\varepsilon}\cdot dr=\frac{\rho_{\ell}}{2\pi\varepsilon}\ln\left(\frac{b}{a}\right) \]

Ahora, la capacitancia total de una sección de línea es

\[\label{eq:4}C_{\text{TOTAL}}=C\Delta z=\frac{Q}{V}=\frac{\rho_{\ell}\Delta z}{V} \]

y así la capacitancia por unidad de longitud de línea es (con unidades SI de\(\text{F/m}\))

\[\label{eq:5}C=\frac{2\pi\varepsilon}{\ln(b/a)} \]

La conductancia de la línea se encuentra comenzando con la densidad de corriente en el dieléctrico, que es

\[\label{eq:6}J=\sigma E+\jmath\omega\varepsilon E \]

Integrando esto sobre el volumen del dieléctrico,

\[\label{eq:7}I=GV+\jmath\omega CV \]

Usando un desarrollo similar al que condujo a la Ecuación\(\eqref{eq:5}\), se encuentra que la conductancia por unidad de longitud es (con las unidades SI de\(\text{S/m}\))

\[\label{eq:8}G=\frac{2\pi\sigma}{\ln(b/a)} \]

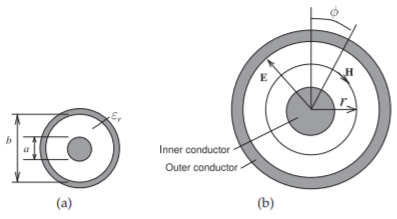
Figura\(\PageIndex{1}\): Línea coaxial: (a) con interior un conductor de radio\(a\) y un conductor externo con radio interior\(b\); y (b) con coordenadas cilíndricas utilizadas en el cálculo.

El desarrollo de las expresiones para\(L\) y\(R\) está más involucrado, ya que habrá corriente en el interior del conductor interno. Para simplificar las cosas se considerará el límite de alta frecuencia donde el efecto piel esté completamente establecido de manera que las corrientes en los conductores interno y externo se limiten a una capa delgada cerca de las superficies de los conductores en el radio\(a\) para el conductor interno y en el radio\(b\) para el exterior conductor. Entonces el campo magnético quedará confinado a la región entre los conductores. Usando la ley circuital de Ampere, Ecuación (1.6.1),

\[\label{eq:9}\oint_{\ell}\overline{H}\cdot d\ell =\oint_{\ell}H_{\phi}\hat{\mathbf{ϕ}}\cdot d\ell =I_{\text{enclosed}}=I \]

donde la integral de línea cerrada está en un círculo de radio constante. Observando que\(H_{r}\) es sólo una función de\(r\), entonces para\(a<r<b\),

\[\label{eq:10}I=2\pi r_{r}(r)\quad\text{and}\quad B_{r}=\mu H_{r}=\frac{\mu I}{2\pi r} \]

Esto permite que la inductancia de línea se calcule como el flujo magnético total (obtenido integrando sobre la sección transversal de la línea coaxial entre radios\(a\) y\(b\)) por unidad de corriente. Entonces la inductancia de la línea por unidad de longitud es

\[\label{eq:11}L=\int_{a}^{b}\left(\frac{\mu}{2\pi r}\right)dr=\frac{\mu}{2\pi}\ln\left(\frac{b}{a}\right) \]

que cuenta con unidades SI de\(\text{H/m}\).

La resistencia de las líneas se calcula utilizando la resistencia superficial de los conductores,\(R_{s}\). Entonces la resistencia de la línea por unidad de longitud es

\[\label{eq:12}R=\frac{R_{s}}{2\pi}\left(\frac{1}{a}+\frac{1}{b}\right) \]

que cuenta con las unidades SI de\(\Omega\text{/m}\).

Entonces la impedancia característica sin pérdidas de la línea coaxial es

\[\label{eq:13}Z_{0}=\sqrt{\frac{L}{C}}=\frac{1}{2\pi}\sqrt{\frac{\mu}{\varepsilon}}\ln\left(\frac{b}{a}\right) \]

que tiene unidades de\(\Omega\) s si todas las cantidades en la expresión están en unidades SI. Se deriva una impedancia característica compleja usando\(Z_{0} = \sqrt{(R + \jmath\omega L)/(G + \jmath\omega C)}\), pero si la pérdida es pequeña, esta estará muy cerca de la impedancia característica sin pérdidas. También

\[\label{eq:14}Z_{0}=\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\frac{1}{2\pi}\sqrt{\frac{\mu_{0}}{\varepsilon_{0}}}\ln\left(\frac{b}{a}\right)=60\sqrt{\frac{\mu_{r}}{\varepsilon_{r}}}\ln\left(\frac{b}{a}\right) \]

Tenga en cuenta que el\(60\) es exacto y no una aproximación.

Para líneas coaxiales reales el dieléctrico tiene pérdidas insignificantes y la resistencia,\(R\), es pequeña. Utilizando los resultados desarrollados en la Sección 2.5.4 para una línea de baja pérdida, el coeficiente de atenuación para una línea coaxial de baja pérdida es, de la Ecuación (2.5.15),

\[\label{eq:15}\alpha\approx\alpha_{c}=\frac{R}{2Z_{0}}=\frac{R_{s}}{2\pi}\left(\frac{1}{a}+\frac{1}{b}\right)\frac{2\pi}{\ln(b/a)}\sqrt{\frac{\varepsilon}{\mu}}=\left(\frac{1}{a}+\frac{1}{b}\right)\frac{R_{s}}{\ln(b/a)}\sqrt{\frac{\varepsilon}{\mu}} \]

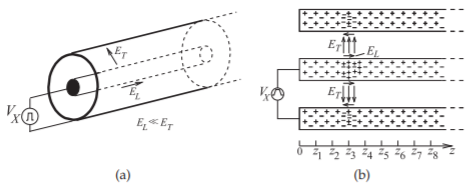
Figura\(\PageIndex{2}\): Una línea de transmisión coaxial: (a) vista tridimensional; (b) la línea con fuente de voltaje pulsado que muestra los campos eléctricos en un instante en el tiempo a medida que un pulso de voltaje viaja por la línea.

que es la atenuación debida al conductor, es decir, debido a la pérdida óhmica o del conductor. De la Ecuación\(\eqref{eq:15}\) se ve que para una impedancia característica dada, y por lo tanto una relación fija\(b/a\), el coeficiente de atenuación y por lo tanto la pérdida, se minimiza cuando la línea tiene una sección transversal grande (es decir, grande\(a\) y\(b\)). Con un fijo\(a\), la atenuación se minimiza con\(b/a = 3.59\) independiente de\(\mu\) y\(\varepsilon\) [17]. Para una línea coaxial llena de aire con\(\mu_{r} =1= \varepsilon_{r}\), la impedancia característica de esta línea de pérdida mínima es\(76.7\:\Omega\). Para una línea coaxial típicamente llena de teflón\(\varepsilon_{r} = 2.1\) y la impedancia característica de una línea de pérdida mínima, de la ecuación\(\eqref{eq:14}\), es\(52.9\:\Omega\). El resultado anterior es cuando la conductividad de los conductores interno y externo es la misma y la inductancia interna de los conductores es insignificante. Si la inductancia interna no es despreciable, o los conductores tienen diferente conductividad, lo que ocurre cuando los conductores no son sólidos, entonces la impedancia característica óptima podría ser mayor o menor [17]. La elección\(50\:\Omega\) de la impedancia característica es un buen compromiso. Se pueden derivar otras dimensiones de línea óptimas para maximizar el voltaje de ruptura y optimizar la transferencia de potencia [22].

La frecuencia de operación superior y las dimensiones de las líneas coaxiales se eligen para asegurar la propagación monomodo [23, 24, 25]. Una aproximación útil a la frecuencia de corte del primer modo de orden superior es [23]

\[\label{eq:16}\lambda_{c}\approx\frac{\pi(a+b)}{2} \]

que es la circunferencia de un círculo a medio camino entre los conductores interno y externo. Dado que\(b\) es varias veces\(a\), entonces el radio del conductor externo determina en gran medida la frecuencia de operación superior. Minimizar la pérdida dada una frecuencia de corte fija del primer modo de orden superior produce otro valor óptimo\(b/a\) de pérdida mínima (ver [22]).

2.9.2 Campos electromagnéticos en una línea coaxial realista

En esta sección se considera una línea coaxial realista con conductores que tienen una pequeña cantidad de pérdida. Esto amplía la discusión en la Sección 2.1.2. Cuando se aplica un impulso de voltaje positivo al conductor central de la línea coaxial, como se muestra en la Figura\(\PageIndex{2}\) (a), resulta un campo eléctrico que se dirige esencialmente desde el conductor central al conductor externo. Un componente mucho más pequeño del campo eléctrico también se dirigirá a lo largo de la línea. Estos campos se muestran en la Figura\(\PageIndex{2}\) (b), donde la dirección del campo eléctrico es la dirección en la que se movería una carga positiva si se liberara al campo. El componente del campo que se dirige a lo largo de la trayectoria más corta desde el conductor central hasta el conductor externo (en el plano transversal)

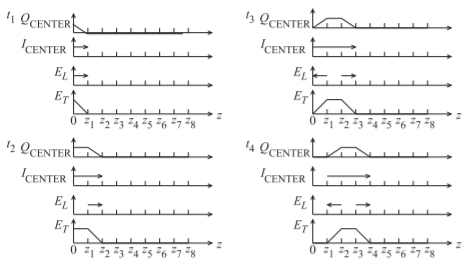
Figura\(\PageIndex{2}\): Campos, corrientes y cargas en la línea de transmisión coaxial de la Figura 2.1.2 a veces\(t_{4} > t_{3} > t_{2} > t_{1}\). \(Q_{\text{CENTER}}\)es el cargo neto gratuito en el conductor central. \(I_{\text{CENTER}}\)es la corriente en el conductor central.

se denota\(E_{T}\), y se denota el componente dirigido a lo largo de la línea\(E_{L}\). (Los subíndices\(T\) y\(L\) denotan componentes transversales y longitudinales, respectivamente.) Así, mientras\(E_{L} ≪ E_{T}\), es necesario acelerar los electrones en los conductores y así dar lugar al flujo de corriente, y de ahí el movimiento del pulso a lo largo de la línea. Los electrones no aceleran indefinidamente, ya que chocan con átomos y se dispersan de manera que hay una velocidad neta de electrones libres a lo largo de los conductores interno y externo.

Las instantáneas de un pulso que viaja a lo largo de una línea se muestran en la Figura\(\PageIndex{2}\) en cuatro momentos diferentes.