4.10: Líneas en Sustratos Semiconductores

La propagación en estructuras de líneas de transmisión fabricadas en sustratos semiconductores puede tener un comportamiento peculiar. El interés en tales líneas está en relación con los circuitos integrados de RF (RFIC) y los circuitos integrados de microondas monolíticos (MMIC) que utilizan tecnologías de silicio y semiconductores compuestos. Más específicamente, las interconexiones en sistemas metal-óxido-semiconductor (MOS) o metal-aislador-semiconductor (MIS), donde existe una capa aislante, tal como óxido, entre el conductor y la oblea semiconductora (ver Figura\(\PageIndex{1}\) (a)), son de interés particular debido a su capacidad para soportar un modo de onda lenta. Un modo de onda lenta se propaga mucho más lento de lo que se esperaría. En el caso de un sustrato semiconductor con conductividad intermedia, el campo magnético penetra en el sustrato pero el campo eléctrico no. Esta separación de campos magnéticos y eléctricos ralentiza la onda. Las estructuras de onda lenta encuentran un uso importante en elementos distribuidos en chip en RF. En particular, un sustrato de silicio puede tener un impacto significativo en la propagación de microbandas que se deriva de la capa de carga formada en la interfaz silicio-dióxido de silicio. El efecto de onda lenta se utiliza en líneas de retardo, acopladores y filtros. Con las líneas de contacto Schottky, el efecto se utiliza en cambiadores de fase variable, filtros sintonizables de voltaje y varias otras aplicaciones.

Ahora, una explicación intuitiva de las características de propagación de líneas de microcinta en sustratos estratificados puede basarse en la estructura de placa paralela mostrada en la Figura\(\PageIndex{2}\). Para un análisis EM exacto del efecto de onda lenta con sustratos de silicio, ver [14]. Además de desarrollar una aproximación muy útil para la importante situación de las líneas de transmisión en un aislante como el óxido de silicio sobre un semiconductor, el tratamiento a continuación indica el tipo de aproximación que se puede utilizar para analizar estructuras inusuales. En esta estructura, asuma un modo de propagación cuasi-tem. En otras palabras, los parámetros de propagación de onda\(\alpha,\:\beta,\) y se\(Z_{0}\) pueden deducir a partir de soluciones electrostáticas y magnetostáticas para los parámetros por unidad de longitud\(C,\: G,\: L,\) y\(R\).

El análisis comienza con un tratamiento del clásico condensador Maxwell—Wagner. La figura\(\PageIndex{3}\) (a) muestra la estructura de dicho condensador donde hay dos materiales diferentes entre las placas paralelas del condensador con diferentes permitividades y conductividades. El circuito equivalente se muestra en

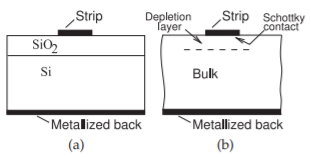
Figura\(\PageIndex{1}\): Líneas de transmisión sobre semiconductor de silicio: (a) sándwich de silicio-dióxido de silicio; y (b) vista a granel.

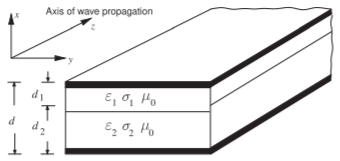
Figura\(\PageIndex{2}\): Estructura de línea de transmisión de placa paralela.

Figura\(\PageIndex{3}\) (b) con los elementos dados por (\(A\)es el área de la placa)

\[\begin{align}\label{eq:1}C_{1}&=\varepsilon_{1}\frac{A}{d_{1}},\: R_{1}=\frac{1}{\sigma_{1}}\frac{d_{1}}{A},\:C_{2}=\varepsilon_{2}\frac{A}{d_{2}},\:R_{2}=\frac{1}{\sigma_{2}}\frac{d_{2}}{A} \\ \label{eq:2}\tau_{1}&=R_{1}C_{1}=\frac{\varepsilon_{1}}{\sigma_{1}},\:\tau_{2}=R_{2}C_{2}=\frac{\varepsilon_{2}}{\sigma_{2}}\end{align} \]

La admisión de toda la estructura a la frecuencia de radián\(\omega\) es

\[\label{eq:3}Y(\omega)=\frac{1}{R_{1}+R_{2}}\frac{(1+\jmath\omega\tau_{1})(1+\jmath\omega\tau_{2})}{1+\jmath\omega\tau} \]

donde

\[\label{eq:4}\tau=\frac{R_{1}\tau_{2}+R_{2}\tau_{1}}{R_{1}+R_{2}} \]

Presentando

\[\label{eq:5}Y(\omega)=\jmath\omega\left(\varepsilon_{e}\frac{A}{d}\right) \]

la permitividad compleja efectiva,\(\varepsilon_{e} = \varepsilon_{e}' −\jmath\varepsilon_{e}''\), puede definirse en términos de Ecuación\(\eqref{eq:3}\). Uso de ecuaciones\(\eqref{eq:3}\) y\(\eqref{eq:5}\) rendimientos

\[\label{eq:6}\varepsilon_{e}'=\frac{\tau_{1}+\tau_{2}-\tau+\tau\tau_{1}\tau_{2}\omega^{2}}{(R_{1}+R_{2})[1+(\omega\tau)^{2}]}\frac{d}{A} \]

Consideremos ahora el caso cuando\(R_{1}\) va al infinito (es decir\(\mathsf{1}\), Capa, la capa superior, en Figura\(\PageIndex{3}\) es un aislante). Para este caso, la ecuación\(\eqref{eq:6}\) se convierte en

\[\label{eq:7}\varepsilon_{e}'=\frac{1+\left(1+\frac{d_{2}}{d_{1}}\frac{\varepsilon_{1}}{\varepsilon_{2}}\right)\left(\frac{\omega\varepsilon_{2}}{\sigma_{2}}\right)^{2}}{1+\left(1+\frac{d_{2}}{d_{1}}\frac{\varepsilon_{1}}{\varepsilon_{2}}\right)^{2}\left(\frac{\omega\varepsilon_{2}}{\sigma_{2}}\right)^{2}}\left(\varepsilon_{1}\frac{d}{d_{1}}\right) \]

Se desprende de Ecuaciones\(\eqref{eq:6}\) y\(\eqref{eq:7}\) que la permitividad compleja efectiva tiene un componente dependiente de la frecuencia. Considera cómo varía esto con algunos casos de\(\omega\). Para\(\omega = 0\), el valor estático de la permitividad efectiva es

\[\label{eq:8}\varepsilon_{e,0}'=\varepsilon_{1}\frac{d}{d_{1}} \]

Para el caso donde\(\omega\) va al infinito (el valor óptico), la parte real de la permitividad efectiva es

\[\label{eq:9}\varepsilon_{e,\infty}'=\frac{\varepsilon_{1}\varepsilon_{2}(d_{1}+d_{2})}{\varepsilon_{2}d_{1}+\varepsilon_{1}d_{2}} \]

Tenga en cuenta también que el valor de se\(\varepsilon_{e,\infty}′\) puede lograr aproximadamente para un gran valor de\(\omega\varepsilon_{2}/\sigma_{2}\) (es decir, se pueden usar sustratos de baja conductividad para asegurar que las corrientes de desplazamiento dominen). De manera similar, es claro que se\(\varepsilon_{e,0}'\) puede lograr teniendo un pequeño valor de\(\omega\varepsilon_{2}/\sigma_{2}\). También tenga en cuenta que se\(\varepsilon_{e,0}'\) puede hacer muy grande haciendo\(d_{1}\) mucho más pequeño que\(d\).

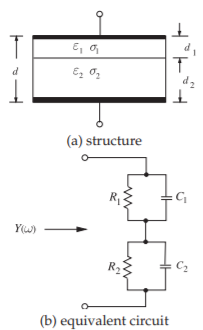
Figura\(\PageIndex{3}\): Capacitor Maxwell—Wagner.

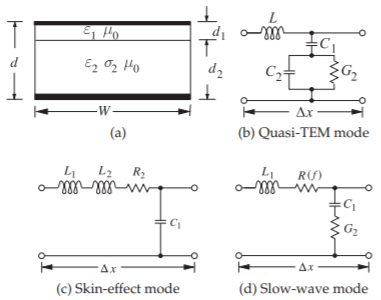
Figura\(\PageIndex{4}\): Modos en una línea de transmisión MOS: (a) estructura equivalente de la línea MOS de la Figura\(\PageIndex{1}\).

Ejemplo\(\PageIndex{1}\): Two-Layer Substrate

Considera la estructura en la Figura\(\PageIndex{2}\). Determinar la longitud de onda guía\(\lambda_{g}\),, y la longitud de onda en el aislador\(\lambda_{1}\),, a una frecuencia de\(1\text{ GHz}\). SiO\(_{2}\) y Si son los dieléctricos, con permitividades\(\varepsilon_{1} = 4\varepsilon_{0}\) y\(\varepsilon_{2} = 13\varepsilon_{0}\) (las conductividades son cero). Las profundidades\(d_{2}\) y\(d_{1}\) de los dos dieléctricos son\(d_{2} = 250\:\mu\text{m}\) y\(d_{1} = 0.1\:\mu\text{m}\).

Solución

\[\begin{align}\lambda_{1}&=\frac{3\times10^{8}}{10^{9}\sqrt{4}}=0.15\text{ m}=15\text{ cm}\nonumber \\ \label{eq:10}\epsilon_{e}&=\frac{\varepsilon_{1}\varepsilon_{2}(d_{1}+d_{2})}{\varepsilon_{1}d_{2}+\varepsilon_{2}d_{1}}=12.99\varepsilon_{0},\quad\lambda_{g}=\frac{3\times10^{8}}{10^{9}\sqrt{12.99}}=0.0832\text{ m}=8.32\text{ cm}\end{align} \]

4.10.1 Modos en la línea MIS (MOS)

La descripción previa de las propiedades de un condensador Maxwell—Wagner conduce a una discusión de los posibles modos en la línea MIS (MOS). Para que el problema sea manejable, la línea de transmisión mostrada en la Figura\(\PageIndex{1}\) (a) se aproximará como teniendo la sección transversal mostrada en la Figura\(\PageIndex{4}\) (a).

Modo cuasi-TEM dieléctrico

El primer modo posible es el modo dieléctrico cuasi-TEM, para lo cual es aplicable el modelo de circuito equivalente seccional de la Figura\(\PageIndex{4}\) (b). En esta modalidad\(\sigma_{2} ≪ \omega\varepsilon_{2}\). Esto implica a partir de la discusión anterior que\(\varepsilon_{e}' = \varepsilon_{e,\infty}'\) y\(\mu_{e}' = \mu_{0}\). Así, los parámetros por unidad de longitud son

\[\label{eq:11}L=\mu_{0}\frac{d_{1}}{W},\quad C_{1}=\varepsilon_{1}\frac{W}{d_{1}},\quad C_{2}=\varepsilon_{2}\frac{W}{d_{2}}m\quad G_{2}=\sigma_{2}\frac{W}{d_{2}} \]

Estos tienen las unidades SI\(\text{H/m}\) para\(L\),\(\text{F/m}\) para\(C_{1}\)\(C_{2}\),\(\text{F/m}\) para y\(\text{S/m}\) para\(G_{2}\).

Modo de efecto piel

El segundo modo posible es el modo de efecto piel, para lo cual es aplicable el modelo de circuito equivalente seccional de la Figura\(\PageIndex{4}\) (c). Aquí,\(\sigma_{2} ≪ \omega\varepsilon_{2}\) es tal que la profundidad de la piel\(\delta_{s} = 1/\sqrt{\pi f\mu_{0}\sigma_{2}}\) en el semiconductor es mucho menor que\(d_{2}\) y

\[\varepsilon_{e}'=\varepsilon_{e,0}',\quad\mu_{e}'=\frac{\mu_{0}}{d}\left(d_{1}+\frac{\delta_{s}}{2}\right) \nonumber \]

Así

\[\begin{align}\label{eq:12}L_{1}&=\mu_{0}\frac{d_{1}}{W},\quad&C_{1}&=\varepsilon_{1}\frac{W}{d_{1}}\\ \label{eq:13}L_{2}&=\mu_{0}\frac{1}{W}\left(\frac{\delta_{s}}{2}\right) &R_{2}&=2\pi f\mu_{0}\frac{1}{W}\left(\frac{\delta_{s}}{2}\right)\end{align} \]

Estos tienen las unidades SI\(\text{H/m}\) para\(L_{1}\) y\(L_{2}\),\(\text{F/m}\) para\(C_{1}\), y\(\Omega\text{/m}\) para\(R_{2}\).

Modo de onda lenta

El tercer modo posible de propagación es el modo de onda lenta [15, 16], para lo cual es aplicable el modelo de circuito equivalente seccional de la Figura\(\PageIndex{4}\) (d). Este modo se produce cuando no\(f\) es tan grande y la resistividad es moderada para que la profundidad de la piel\(\delta_{s}\),, sea mayor que (o del orden de)\(d_{2}\). Así\(\varepsilon_{e}' =\varepsilon_{e,0}'\), pero\(\mu_{e}' =\mu_{0}\). Por lo tanto

\[\label{eq:14}v_{p}=\frac{1}{\sqrt{\varepsilon_{e}'\mu_{e}'}}=\frac{1}{\sqrt{\mu_{0}\varepsilon_{0}}}\frac{1}{\sqrt{\varepsilon_{1}}}\sqrt{\frac{d_{1}}{d}} \]

(con unidades SI de\(\text{m/s}\)) y\(\lambda_{g} =\lambda_{1}\sqrt{d_{1}/d}\), donde\(\lambda_{1}\) esta la longitud de onda en el aislador.