4.13: Ejercicios

1. La acumulación de corriente y el efecto de la piel dan como resultado que la pérdida de la línea de transmisión aumente con
   1. Mostrar el apilamiento actual en un diagrama transversal de la línea de microcinta.
   2. Describir el efecto de la piel en un diagrama transversal de la línea de microcinta.
2. ¿Cuál es la profundidad de la piel en una línea de microcinta de cobre\(10\text{ GHz}\)? Supongamos que la conductividad del cobre depositado que forma la tira es la mitad de la del cobre monocristalino a granel. Utilice los datos de la tabla de la página 130.
3. ¿Cuál es la profundidad de la piel en una línea de microcinta plateada\(1\text{ GHz}\)? Supongamos que la conductividad del conductor de plata fabricado es\(75\%\) la de la plata monocristalina a granel. Utilice los datos de la tabla de la página 130.
4. ¿Cuál es la fuente dominante de dispersión en una línea de transmisión de microcinta?
5. Usando la Figura 4.3.3, determinar la impedancia característica compleja y la permitividad efectiva compleja de una línea de microcinta en\(12\text{ GHz}\). La línea se fabrica sobre alúmina con\(\varepsilon_{r}(0) = 9.9,\: w = 240\:\mu\text{m},\: h = 500\:\mu\text{m}\).
6. Una pared magnética y una pared eléctrica están\(2\text{ cm}\) separadas y están separadas por un material sin pérdidas que tiene una permitividad relativa\(10\) y una permeabilidad relativa de\(23\). ¿Cuál es la frecuencia de corte del modo de orden más bajo en este sistema?
7. Describir el modo de resonancia transversal en línea de banda. ¿Cuándo puede ocurrir?
8. La tira de una microtira tiene un ancho de\(600\:\mu\text{m}\) y se fabrica sobre un sustrato sin pérdidas que es\(1\text{ mm}\) grueso y tiene una permitividad relativa de\(10\).
   1. Dibuje el modelo de guía de ondas de microcinta de la línea de microcinta. Pon dimensiones en tu dibujo.
   2. Dibuje la distribución del campo eléctrico del primer modo de resonancia transversal y calcule la frecuencia a la que ocurre el modo de resonancia transversal.
   3. Dibuje la distribución del campo eléctrico del primer modo de microcinta de orden superior y calcule la frecuencia a la que ocurre.
   4. Dibuje la distribución del campo eléctrico del modo de losa y calcule la frecuencia a la que ocurre.
9. Una línea de microcinta tiene un ancho de\(352\:\mu\text{m}\) y está construida sobre un sustrato que es\(500\:\mu\text{m}\) grueso con una permitividad relativa de\(5.6\).
   1. Determinar la frecuencia a la que se produciría primero la resonancia transversal.
   2. Cuando el dieléctrico tiene un grosor ligeramente inferior a un cuarto de longitud de onda, se puede soportar el modo de losa dieléctrica. Algunos de los campos aparecerán tanto en la región del aire como en el dieléctrico, extendiendo el grosor efectivo del dieléctrico. Ignorando los campos en el aire (use un criterio de un cuarto de longitud de onda), ¿a qué frecuencia ocurrirá primero el modo de losa dieléctrica?
10. La tira de una microtira tiene un ancho de\(600\:\mu\text{m}\) y utiliza un sustrato sin pérdidas que es\(635\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(4.1\).
    1. ¿A qué frecuencia ocurrirá la primera resonancia transversal?
    2. ¿A qué frecuencia ocurrirá el primer modo de microcinta de orden superior?
    3. ¿A qué frecuencia ocurrirá el modo losa?
    4. Identificar el rango de frecuencia útil de operación de la microcinta.
11. El espacio de diseño para líneas de transmisión en diseños de microcinta está determinado por el líder del proyecto de diseño a ser\(20–100\:\Omega\). El sustrato preferido tiene un espesor de\(500\:\mu\text{m}\) y una permitividad relativa de\(8\). Cuál es el rango máximo de frecuencia de funcionamiento de los diseños soportados por esta elección de tecnología. Ignorar los efectos de dispersión de frecuencia (es decir, dependencia de frecuencia de permitividad efectiva y pérdidas). [Pista: Primero determine las dimensiones de la tira que proporcionará el rango de impedancia requerido y luego determine la frecuencia a la que ocurre el multimodo de orden más bajo.]
12. Considerar el diseño de líneas de transmisión en tecnología de microcinta utilizando un sustrato sin pérdidas con una permitividad relativa\(10\) y espesor de\(400\:\mu\text{m}\). Usted querrá utilizar las fórmulas de la Sección 3.5.3.
    1. ¿Cuál es la impedancia característica máxima que se puede lograr para una línea de transmisión fabricada con esta tecnología?
    2. Trazar la impedancia característica frente al ancho de banda.
    3. Por consideraciones de tolerancia de fabricación, el ancho mínimo de banda que se puede fabricar es\(20\:\mu\text{m}\). ¿Cuál es la impedancia característica máxima que se puede lograr en la práctica?
    4. Si el rango de frecuencia de operación es\(1– 10\text{ GHz}\), determine el ancho máximo de la tira a partir de consideraciones de modo de orden superior. Debe considerar el modo de resonancia transversal así como los modos de microcinta de orden superior.
    5. Identificar el espacio de diseño eléctrico (es decir, el rango de impedancia característico alcanzable).
    6. Identificar el espacio físico de diseño (es decir, el rango de anchos de banda aceptables).
    7. Si el espacio de diseño eléctrico requiere que las impedancias de la línea de transmisión se logren dentro\(±2\:\Omega\), ¿qué tolerancia se debe lograr en el proceso de fabricación si el grosor del sustrato se puede lograr exactamente? [Pista: Primero identifique la esquina crítica del proceso físico y, por lo tanto, el ancho crítico de la tira que es más susceptible a las variaciones de ancho. Luego determine la tolerancia en el ancho de la banda para lograr la variación de impedancia característica permisible. Es decir, la impedancia característica es una función del ancho y la altura de la tira. Si el sustrato es perfecto (sin variación de altura), entonces ¿cuánto puede variar el ancho de la tira para mantener la impedancia dentro\(±2\:\Omega\) del valor deseado? Puedes resolver esto gráficamente usando una gráfica de\(Z_{0}\) versus ancho o puedes llegar iterativamente a la respuesta recalculando\(Z_{0}\).]
    8. Si el espacio de diseño eléctrico requiere que las impedancias de la línea de transmisión se logren dentro\(±2\:\Omega\), ¿qué tolerancia se debe lograr en el proceso de fabricación si la tolerancia del espesor del sustrato es\(±2\:\mu\text{m}\)? Si el sustrato no es perfecto (la variación de altura es\(±2\:\mu\text{m}\)), entonces ¿cuánto puede variar el ancho de la tira para mantener la impedancia dentro\(±2\:\Omega\) del valor deseado? Este problema es directamente aplicable a las compensaciones de procesos/diseño del mundo real.
13. La tira de una microtira tiene un ancho de\(500\:\mu\text{m}\) y se fabrica sobre un sustrato sin pérdidas que es\(635\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(12\). [Ejemplos de Parallels 4.6.1, 4.6.2 y 4.6.3]
    1. ¿A qué frecuencia ocurre primero la resonancia transversal?
    2. ¿A qué frecuencia se propaga primero el primer modo de microbanda de orden superior?
    3. ¿A qué frecuencia ocurre primero el modo de sustrato (o losa)?
14. La tira de una microtira tiene un ancho de\(250\:\mu\text{m}\) y utiliza un sustrato sin pérdidas que es\(300\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(15\).
    1. ¿A qué frecuencia ocurre primero la resonancia transversal?
    2. ¿A qué frecuencia se propaga el primer modo de microcinta de orden superior?
    3. ¿A qué frecuencia ocurre primero el modo de sustrato (o losa)?
    4. ¿Cuál es la frecuencia de operación más alta de la microcinta?
15. Una línea de microcinta tiene un ancho de banda de\(100\:\mu\text{m}\) y se fabrica sobre un sustrato que es\(150\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(9\).
    1. Dibuje el modelo de guía de ondas de microcinta e indique y calcule las dimensiones del modelo.
    2. Con base únicamente en el modelo de guía de ondas de microcinta, ¿determinar la frecuencia a la que se produce la primera resonancia transversal?
    3. Con base en el modelo de guía de ondas de microcinta, ¿determinar la frecuencia a la que se produce el primer modo de microbanda de orden superior?
    4. ¿A qué frecuencia ocurrirá el modo losa? Para ello no se puede utilizar el modelo de guía de ondas de microcinta.
16. Una línea de microcinta tiene un ancho de banda de\(100\:\mu\text{m}\) y se fabrica sobre un sustrato que es\(150\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(9\).
    1. Definir las propiedades de una pared magnética.
    2. Identificar dos situaciones en las que se pueda utilizar una pared magnética en el análisis de una línea de microcinta; es decir, dar dos situaciones donde se pueda utilizar una aproximación de pared magnética.
    3. Dibuje el modelo de guía de ondas de microcinta e indique y calcule las dimensiones del modelo.
17. Considerar el diseño de líneas de transmisión en tecnología de microcinta utilizando un sustrato sin pérdidas con permitividad relativa\(20\) y espesor de\(200\:\mu\text{m}\).
    1. Utilizando argumentos cualitativos, muestran que la impedancia característica máxima que se puede lograr para una línea de transmisión fabricada en esta tecnología es\(116\:\Omega\). El máximo no lo es en realidad\(116\:\Omega\), pero un simple argumento te llevará a esta conclusión.
    2. Trazar la impedancia característica versus el ancho del sustrato.
    3. Por consideraciones de tolerancia de fabricación, el ancho mínimo de banda que se puede fabricar es\(20\:\mu\text{m}\). ¿Cuál es la impedancia característica máxima que se puede lograr en la práctica?
    4. Si el rango de frecuencia de operación es\(2– 18\text{ GHz}\), determine el ancho máximo de la tira a partir de consideraciones de modo de orden superior. Debe considerar el modo de resonancia transversal, el modo de orden superior y el modo de losa.
    5. Identificar el espacio de diseño eléctrico (es decir, el rango de impedancia característico).
    6. Identificar el espacio físico de diseño (es decir, el rango de anchos de banda aceptables).
    7. Si el espacio de diseño eléctrico requiere que las impedancias de la línea de transmisión se logren dentro\(±2\:\Omega\), ¿qué tolerancia se debe lograr en el proceso de fabricación si el grosor del sustrato se puede lograr exactamente? [Pista: Primero identifique la esquina crítica del proceso físico y, por lo tanto, el ancho crítico de la tira que es más susceptible a las variaciones de ancho. Luego determine la tolerancia en el ancho de la tira para lograr la variación de impedancia característica permisible.]
    8. Si el espacio de diseño eléctrico requiere que las impedancias de la línea de transmisión se logren dentro\(±2\:\Omega\), ¿qué tolerancia se debe lograr en el proceso de fabricación si la tolerancia del espesor del sustrato es\(±2\:\mu\text{m}\)?
18. La tira de una línea de microcinta tiene un ancho de\(0.5\text{ mm}\), y el sustrato de microcinta es\(1\text{ mm}\) grueso y tiene una permitividad relativa\(9\) y permeabilidad relativa de\(1\).
    1. Dibuje el modelo de guía de ondas de microcinta y calcule las dimensiones del modelo. Mostrar claramente las paredes eléctricas y magnéticas en el modelo.
    2. Utilizar el modelo de guía de ondas microstrip para calcular la frecuencia de corte del modo de resonancia transversal?
    3. Un modo de sustrato también se puede excitar pero la frecuencia de corte de este modo no se puede calcular usando el modelo de guía de ondas de microbanda. Proporcionar una breve descripción del modo sustrato y calcular la frecuencia más baja a la que puede existir.
19. Una tecnología de microcinta utiliza un sustrato con una permitividad relativa\(10\) y espesor de\(400\:\mu\text{m}\). Si la frecuencia de operación es\(10\text{ GHz}\), cuál es el ancho máximo de la tira a partir de consideraciones de modo de orden superior.
20. Una línea de microcinta que opera en\(18\text{ GHz}\) tiene un sustrato\(200\:\mu\text{m}\) grueso con una permitividad relativa de\(20\).
    1. Determine el ancho máximo de la tira a partir de consideraciones de modo de orden superior. Considere el modo de resonancia transversal, el modo de microbanda de orden superior y el modo de losa.
    2. Determinar así la impedancia característica mínima alcanzable.
21. Una línea de microcinta tiene un ancho de banda de\(100\:\mu\text{m}\) y se fabrica sobre un sustrato\(150\:\mu\text{m}\) grueso sin pérdidas con una permitividad relativa de\(9\).
    1. Definir las propiedades de una pared magnética.
    2. Identifique dos situaciones en las que se pueda utilizar una pared magnética para determinar el multimodo en una línea de microcinta. Es decir, dar dos ubicaciones donde se pueda utilizar una aproximación de pared magnética.
22. Dos paredes magnéticas están separadas por\(1\text{ mm}\) en un material sin pérdidas que tiene una permitividad relativa de\(9\) y una permeabilidad relativa de\(1\).
    1. ¿Cuál es la longitud de onda de una\(10\text{ GHz}\) señal en este material?
    2. Consideremos ahora una variación de campo, es decir, un modo y no constante, establecida por las paredes magnéticas. Describa esta variación de campo de orden más baja. ¿Es así como varía el\(\text{H}\) campo o cómo varía el\(\text{E}\) campo (uno es suficiente)?
    3. ¿Cuál es la frecuencia más baja a la que una variación de campo puede ser soportada por esas paredes en el medio especificado?
23. Una línea de microcinta tiene un ancho de banda de\(250\:\mu\text{m}\) y un sustrato\(300\:\mu\text{m}\) grueso con una permitividad relativa de\(15\). ¿A qué frecuencia puede ocurrir primero el modo sustrato?
24. Una línea de microcinta tiene un ancho de banda de\(250\:\mu\text{m}\) y un sustrato\(300\:\mu\text{m}\) grueso con una permitividad relativa de\(15\). ¿A qué frecuencia se puede propagar primero un modo de microbanda de orden superior?
25. Una línea de microcinta tiene un ancho de banda de\(200\:\mu\text{m}\) y un sustrato que es\(400\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(4\). Utilice el modelo de guía de ondas de microcinta para determinar la frecuencia más baja a la que puede ocurrir el modo de microcinta de orden superior.
26. Una línea de microcinta tiene un ancho de banda de\(250\:\mu\text{m}\) y un sustrato\(300\:\mu\text{m}\) grueso con una permitividad relativa de\(15\). ¿A qué frecuencia puede ocurrir primero la resonancia transversal?
27. La siguiente figura es la sección transversal de una línea de transmisión de guía de ondas coplanaria de tierra finita (FGCPW) sobre un plano de tierra. El FGCPW consiste en las tiras de tierra de ancho\(w_{1}\) y la tira de ancho\(w\). Ahora\(w_{1} = 2.5\times s,\: w = 1.3\times s,\) y\(h = 4\times s\). El espesor es\(t = 0.3\times s\).

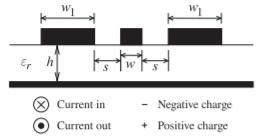
Figura\(\PageIndex{1}\)

1. Ignora el plano de tierra inferior por ahora. Redibuje la estructura e indique las distribuciones de carga y corriente a frecuencias de microondas usando la convención mostrada. En la franja fluye la corriente y la carga es positiva.
2. ¿Esta estructura soporta un modo EM transversal?
3. Nuevamente ignorando el plano de tierra inferior, vuelva a dibujar la estructura e indicar la región donde se concentra la energía.
4. Ahora considere la estructura completa. Si la longitud de onda guía es\(\lambda_{g}\), y la longitud de onda en el dieléctrico es\(\lambda\), indicar el criterio para la frecuencia más baja a la que la resonancia transversal se convertirá en un problema.

28. Utilice un diagrama para mostrar los\(H\) campos\(E\) y del modo de microcinta en CPW de tierra finita.
29. ¿El CPW de tierra finito soporta un modo de resonancia transversal? Explique.
30. Para una línea CPW de tierra finita ilustrar los siguientes modos y las condiciones bajo las cuales ocurren.
    1. El modo de microcinta.
    2. El modo cruzado (los planos de tierra no tienen el mismo potencial).
    3. El modo de modo transversal.
31. Considere una línea de cinta simétrica con los siguientes parámetros: espesor total del sustrato\(d = 1.7\text{ mm}\); ancho de la tira\(w = 2.5\text{ mm}\); permitividad relativa del sustrato\(= 9\); y frecuencia de operación\(= 30\text{ GHz}\).
    1. ¿Cuál es el valor de la permitividad efectiva?
    2. ¿Cuál es el valor de la longitud de onda del espacio libre?
    3. ¿Cuál es el valor de la longitud de onda guía?
32. ¿Cuál es la causa dominante de dispersión en una línea de cinta? Es decir, lo que es más probable que cause dependencia de frecuencia de la impedancia característica y constante de propagación de la línea.
33. La tira de una línea de microcinta tiene un ancho de\(200\:\mu\text{m}\) y el sustrato es\(400\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(4\).
    1. Dibuje el modelo de guía de ondas efectivo de una línea de microcinta con paredes magnéticas y un ancho de banda efectivo,\(w_{\text{eff}}\).
    2. ¿Cuál es la permitividad relativa efectiva del modelo de guía de ondas de microcinta?
    3. ¿Qué es\(w_{\text{eff}}\)?
    4. ¿Se puede determinar la frecuencia más baja a la que se produce primero el modo de resonancia transversal a partir del modelo de guía de ondas de microcinta?
34. La tira de una línea de cinta simétrica tiene un ancho de\(200\:\mu\text{m}\) y está incrustada en un medio sin pérdidas que es\(400\:\mu\text{m}\) grueso y tiene una permitividad relativa de\(13\), así la separación,\(h\), de la tira a cada uno de los planos de tierra es\(200\:\mu\text{m}\).
    1. Dibuje el modelo de guía de onda de una línea de cinta con paredes magnéticas y un ancho de banda efectivo\(w_{\text{eff}}\), que será aproximadamente el mismo que con una línea de microcinta.
    2. ¿Cuál es la permitividad relativa efectiva del modelo de guía de onda de línea de banda?
    3. ¿Qué es\(w_{\text{eff}}\)?
    4. ¿A qué frecuencia ocurrirá la primera resonancia transversal?
    5. ¿A qué frecuencia ocurrirá el primer modo de línea de banda de orden superior?
    6. ¿A qué frecuencia ocurrirá el primer modo de guía de ondas de placa paralela? No consideres el modo sin variación de campo, ya que esto no puede ser excitado.
    7. Identificar el rango de frecuencia útil de operación de la línea de cinta.
35. Describa el modo de placa paralela en la línea de cinta.
36. Considera la estructura en la Figura 4.10.2. Determine la longitud de onda guía\(\lambda_{g}\),, y la longitud de onda en el aislador superior\(\lambda_{1}\),, a una frecuencia de\(20\text{ GHz}\). Las permitividades son\(\varepsilon_{1} = 3.9\varepsilon_{0}\) y\(\varepsilon_{2} = 13\varepsilon_{0}\). Las profundidades de los dieléctricos son\(d_{2} = 100\:\mu\text{m}\) y\(d_{1} = 1.0\:\mu\text{m}\). [Ejemplo de Parallels 4.10.1]
37. Considerar un medio de transmisión metal-óxido-semiconductor tal como se examina en la Sección 4.10. La estructura en forma de un condensador Maxwell—Wagner se muestra en la Figura 4.10.3 (a) con\(d_{1} = 100\:\mu\text{m},\: d_{2} = 500\:\mu\text{m}\), y permitividades relativas\(\varepsilon_{r1} = 3.9\) y\(\varepsilon_{r2} = 13\). Ignorar la conductividad finita. ¿Cuál es el modelo de capacitancia de esta estructura (ver Figura 4.10.3 (b)) y cuáles son los valores de las capacitancias?

4.13.1 Ejercicios por Sección

\(†\)desafiante,\(‡\) muy desafiante

\(§4.2\: 1†, 2, 3\)

\(§4.3\: 4†\)

\(§4.4\: 5\)

\(§4.5\: 6, 7 \)

\(§4.6\: 8†, 9†, 10†, 11‡, 12‡, 13†, 14†, 15†, 16†, 17‡, 18†, 19, 20, 21, 22, 23, 24, 25, 26\)

\(§4.7\: 27‡, 28, 29, 30\)

\(§4.8\: 31‡, 32†, 33†, 34‡, 35\)

\(§4.10\: 36, 37†\)

4.13.2 Respuestas a ejercicios seleccionados

3. \(2.315\:\mu\text{m}\)

6. \(247\text{ MHz}\)

8. c)\(25\text{ GHz}\)
9. (c)\(\text{DC}\) a\(63.4\text{ GHz}\)
10. (d)\(\text{DC}\leq f\leq 48.6\text{ GHz}\)

14. \(104.6\text{ GHz}\)

17. (a)\(116\:\Omega\)

17. f)\(20\:\mu\text{m}<w<1.96\text{ mm}\)
18. b)\(55.6\text{ GHz}\)

34. \(207.9\text{ GHz}\)