5.14: Ejercicios

1. Considere la sección transversal de una línea de transmisión acoplada, como se muestra en la Figura 5.2.1, con modos par e impar ambos viajando fuera de la página.
   1. Para un modo par en la línea acoplada, considere un voltaje fasor de\(1\text{ V}\) en cada una de las líneas por encima del plano de tierra en\(0\text{ V}\). Esbozar el campo eléctrico dirigido en el plano transversal, es decir, mostrar la dirección del campo eléctrico.
   2. Para el modo par, esboce los campos magnéticos dirigidos en el plano transversal (el plano de la sección transversal).
   3. Para un modo impar en la línea acoplada, considere un voltaje de fasor de\(+1\text{ V}\) en la línea izquierda y un voltaje de fasor de\(−1\text{ V}\) en la línea derecha. Esboce los campos eléctricos dirigidos en el plano transversal (el plano de la sección transversal).
   4. Para el modo impar, esboce los campos magnéticos dirigidos en el plano transversal (el plano de la sección transversal).
2. El software EM se puede utilizar para determinar los parámetros de modo par e impar de una línea acoplada. Esto generalmente se hace estableciendo el voltaje del fasor en la línea acoplada y evaluando la carga del fasor para cada condición. El voltaje aplicado a la tira izquierda es\(V_{1}\) y el voltaje aplicado a la tira derecha es\(V_{2}\). Las cargas fasoras en las tiras son\(Q_{1}\) y\(Q_{2}\), respectivamente. El análisis se repite con el sustrato reemplazado por espacio libre. En este caso, los cargos se denotan por\(Q_{01}\) y\(Q_{02}\). Las mediciones (basadas en computadora) siguen. [Ejemplo de Parallels 5.5.1]

   Cargar	\(V_{1}=1\text{ V}\); \(V_{2}=-1\text{ V}\)	\(V_{1}=1\text{ V}\); \(V_{2}=1\text{ V}\)
   \(Q_{1}\)\((\text{pC/m})\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=-1\text{ V}\) “>\(40\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=1\text{ V}\) “>\(20\)
   \(Q_{2}\)\((\text{pC/m})\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=-1\text{ V}\) “>\(-50\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=1\text{ V}\) “>\(30\)
   \(Q_{01}\)\((\text{pC/m})\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=-1\text{ V}\) “>\(13.25\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=1\text{ V}\) “>\(6\)
   \(Q_{02}\)\((\text{pC/m})\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=-1\text{ V}\) “>\(-10\)	\ (V_ {1} =1\ texto {V}\);\(V_{2}=1\text{ V}\) “>\(2.75\)

   
   Mesa\(\PageIndex{1}\)
   1. ¿Qué es la matriz de capacitancia de dos puertos?
   2. ¿Cuál es la capacitancia de modo par?
   3. ¿Cuál es la capacitancia en modo impares?
   4. ¿Qué es la matriz de capacitancia de dos puertos de espacio libre (sin dieléctrico)?
   5. ¿Cuál es la capacitancia de modo par en espacio libre?
   6. ¿Cuál es la capacitancia en modo impares de espacio libre?
   7. ¿Cuál es la permitividad relativa efectiva de modo par?
   8. ¿Cuál es la permitividad relativa efectiva en modo extraño?
3. Dos líneas de\(50\:\Omega\) microcinta deben correr paralelas entre sí en una placa\(1\text{ mm}\) de circuito impreso de espesor con una permitividad relativa\(\varepsilon_{r} = 4\). La señal en las líneas es\(3\text{ GHz}\). La permitividad efectiva de las líneas es\(3.1\) y se determina que la distancia aproximada sobre la que las líneas serán paralelas es\(1.42\text{ cm}\). El acoplamiento de las señales en las líneas debe ser al menos\(30\text{ dB}\) hacia abajo.
   1. ¿Cuál es la longitud de onda del espacio libre\(\lambda_{0}\), de la señal?
   2. ¿Cuál es la longitud de onda guía\(\lambda_{g}\),, de la señal?
   3. ¿Cuánto tiempo es el recorrido paralelo de las líneas de microcinta en términos de\(\lambda_{g}\)?
   4. ¿Cuál es el factor de acoplamiento de línea paralela máximo requerido? Explica tu razonamiento.
   5. ¿Cuál es la separación mínima de las líneas? Explica tu razonamiento.
4. Un par de líneas acopladas tiene una permitividad efectiva de modo par\(\varepsilon_{ee}\), de\(4.9\) y una permitividad efectiva de modo impar de\(5.2\).
   1. ¿Cuál es la velocidad de fase de modo par?
   2. ¿Cuál es la velocidad de fase en modo impares?
5. Un acoplador direccional que utiliza líneas acopladas se construye sobre un sustrato de alúmina de espesor\(300\:\mu\text{m}\) y\(\varepsilon_{r} = 10\). Las líneas son\(250\:\mu\text{m}\) anchas y la separación de brechas es\(100\:\mu\text{m}\). Cuáles son (a) las impedancias características, (b) las permitividades efectivas, y (c) las velocidades de fase del modo par e impar de la línea acoplada. (Pista: Si usa una tabla, debe usar la interpolación como se describe en la Sección 1.A.12.)
6. Un acoplador direccional ideal no tiene pérdidas y no hay reflejos en los puertos. Si el factor de acoplamiento es\(10\), ¿cuál es la magnitud del coeficiente de transmisión?
7. Un acoplador direccional tiene las siguientes características: factor de acoplamiento\(C = 20\)\(0.9\), factor de transmisión y factor de directividad\(25\text{ dB}\). Además, el acoplador está emparejado para que no haya reflexión en ninguno de los puertos. ¿Cuál es el aislamiento en decibelios?
8. Un acoplador\(6\text{ dB}\) direccional con pérdidas se hace coincidir para que no haya reflexión en ninguno de los puertos. La pérdida de inserción (considerando el camino pasante) es\(2\text{ dB}\). Si\(1\text{ mW}\) es entrada al acoplador direccional, ¿cuál es la potencia en microvatios disipada en el acoplador direccional? Ignorar la alimentación dejando el puerto aislado.
9. Un acoplador direccional\(1\text{ GHz}\) de microcinta tiene un factor de acoplamiento de\(20\text{ dB}\). El acoplador debe tener una impedancia del sistema de\(50\:\Omega\).
   1. Dibuje el diseño del acoplador direccional.
   2. ¿Cuál es la impedancia de modo par del acoplador?
   3. ¿Cuál es la impedancia de modo impares del acoplador?
   4. ¿Cuál es la longitud eléctrica óptima del acoplador direccional en grados en la frecuencia central de diseño?
   5. Si, además, el aislamiento del acoplador direccional es\(40\text{ dB}\), ¿cuál es su directividad en decibelios?
10. Un acoplador direccional que comprende un par acoplado de líneas de microcinta se va a diseñar en un\(75\:\Omega\) sistema. El factor de acoplamiento es\(10\).
    1. ¿Cuál es la impedancia del sistema\(Z_{0S}\)?
    2. ¿Cuál es la impedancia de modo impares del acoplador?
    3. ¿Cuál es la impedancia de modo par del acoplador?
11. Un acoplador direccional emparejado tiene un factor\(C\) de acoplamiento de\(20\), factor de transmisión\(0.9\), y directividad de\(25\text{ dB}\). ¿Cuál es la potencia disipada en el acoplador direccional si la potencia de entrada a Port\(\mathsf{1}\) es\(1\text{ W}\).
12. Desarrollar el diseño de un acoplador\(10\text{ dB}\) direccional utilizando líneas de microcinta acopladas y un sustrato con una permitividad de\(10\), un espesor de sustrato\(h\),, de\(600\:\mu\text{m}\), y una frecuencia central de\(1\text{ GHz}\). Desarrollar el diseño eléctrico del acoplador (es decir, encontrar las impedancias de modo par e impar requeridas) y luego desarrollar el diseño físico (con anchos y longitudes) del acoplador direccional. Utilice una impedancia del sistema de\(50\:\Omega\).
13. Diseñar un acoplador direccional de microcinta con las siguientes especificaciones: Tecnología de línea de
    transmisión: Coeficiente de
    acoplamiento de microcinta, Impedancia\(C: 20\text{ dB}\)
    característica,\(Z_{0S}\): Permitividad del\(50\:\Omega\)
    sustrato,\(\varepsilon_{r}\): \(4.0\)
    Grosor del sustrato,\(h\): Frecuencia\(635\:\mu\text{m}\)
    central,\(f_{0}\):\(10\text{ GHz}\).
14. Un acoplador direccional que utiliza líneas acopladas se construye sobre un sustrato de alúmina de espesor\(300\:\mu\text{m}\). Las líneas son\(250\:\mu\text{m}\) anchas y la separación de brechas es\(100\:\mu\text{m}\). ¿Cuáles son las impedancias características, las permitividades efectivas y las velocidades de fase de los modos par e impar de la línea acoplada? El puerto\(\mathsf{1}\) es la entrada, el puerto\(\mathsf{2}\) es la salida pasante y el puerto\(\mathsf{3}\) es la salida acoplada. (Pista: Ver Tabla 5.8.3.)
    1. Dibuje el esquema del acoplador direccional y etiquete los puertos.
    2. ¿Cuál es el coeficiente de transmisión del acoplador?
    3. ¿Se puede determinar la directividad del acoplador? Si es así, ¿cuál es la directividad\(D\),, del acoplador?
15. Considere un par de líneas de microcinta paralelas separadas por un espaciado,\(s\), de\(100\:\mu\text{m}\).
    1. ¿Qué sucede con el factor de acoplamiento de las líneas a medida que\(s\) reduce?
    2. ¿Qué sucede con la impedancia del sistema ya que\(s\) reduce y ninguna otra dimensión cambia?
    3. En cuanto a longitudes de onda, ¿cuál es la longitud óptima de las líneas acopladas para el acoplamiento máximo?
16. ¿Cuál es el factor de acoplamiento de un acoplador Lange en decibelios?
17. Considere la sección de línea acoplada interdigital de circuito abierto en la Tabla 5.9.1. Si la línea acoplada es\(\lambda/4\) larga, anote los\(ABCD\) parámetros simplificados. Asumir eso\(\theta_{o} = \theta_{e}\).
18. Considere la sección de línea acoplada simétrica cortocircuitada en el Cuadro 5.9.1. Si la línea acoplada es\(\lambda/4\) larga, anote los\(ABCD\) parámetros simplificados. Asumir eso\(\theta_{o} =\theta_{e}\).
19. Considere la sección de línea acoplada de combinación de circuito abierto en la Tabla 5.9.1. Si la línea acoplada es\(\lambda/4\) larga, anote los\(ABCD\) parámetros simplificados. Asumir eso\(\theta_{o} =\theta_{e}\).
20. Considere la sección de línea acoplada interdigital cortocircuitada en la Tabla 5.9.1. Si la línea acoplada es\(\lambda/4\) larga, anote los\(ABCD\) parámetros simplificados. Asumir eso\(\theta_{o} =\theta_{e}\).
21. Una línea de microcinta acoplada tiene una impedancia de modo impar\(30\:\Omega\) y una impedancia de modo par de\(65\:\Omega\).
    1. ¿Cuál es la impedancia característica diferencial de las líneas acopladas?
    2. ¿Cuál es la impedancia característica de modo común de las líneas acopladas?
22. Un par de líneas de microcinta acopladas tiene impedancias características de modo impar y par de\(60\:\Omega\) y\(70\:\Omega\) respectivamente. Si una resistencia de carga\(R_{L}\),, se coloca al final de las líneas de una tira a la otra, ¿cuál es el valor de\(R_{L}\) para no reflejo del modo par?
23. Las líneas acopladas a continuación tienen impedancias características de modo impar y par de\(30\:\Omega\) y\(60\:\Omega\) respectivamente.

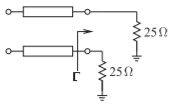
Figura\(\PageIndex{1}\)

1. ¿Cuál es el coeficiente de reflexión en modo impares\(\Gamma\)?
2. ¿Cuál es la impedancia característica de modo común de las líneas acopladas?

24. Las líneas acopladas a continuación tienen impedancias características de modo impar y par de\(60\:\Omega\) y\(100\:\Omega\) respectivamente. Las líneas acopladas tienen una longitud\(\ell\) y ésta es\(\lambda/4\) larga para el modo impar.

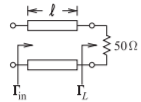
Figura\(\PageIndex{2}\)

1. ¿Cuál es el coeficiente de reflexión en modo impares en la carga, llama a esto\(\Gamma_{Lo}\)?
2. ¿Cuál es el coeficiente de reflexión en modo impares en la entrada a las líneas acopladas?

25. Las líneas de microcinta acopladas a continuación tienen una impedancia característica de modo impar\(40\:\Omega\) y una impedancia característica de modo par de\(75\:\Omega\).

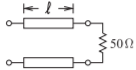
Figura\(\PageIndex{3}\)

1. ¿Cuál es la impedancia característica de modo diferencial?
2. ¿Cuál es la impedancia característica de modo común?

26. Las líneas acopladas a continuación tienen impedancias características de modo impar y par de\(40\:\Omega\) y\(75\:\Omega\) respectivamente.

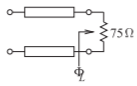
Figura\(\PageIndex{4}\)

1. ¿Cuál es la impedancia característica de modo diferencial\(Z_{0d}\)?
2. ¿Cuál es la resistencia de carga de modo diferencial\(Z_{Ld}\)?
3. ¿Cuál es el coeficiente de reflexión de modo diferencial\(\Gamma_{Ld}\),, a la carga?
4. ¿Cuál es el coeficiente de reflexión en modo impares\(\Gamma_{Ld}\),, a la carga?

27. Las líneas acopladas a continuación tienen impedancias características de modo impar y par de\(60\:\Omega\) y\(100\:\Omega\) respectivamente. Las líneas acopladas tienen una longitud\(\ell\) y ésta es\(\lambda/4\) larga para el modo impar.

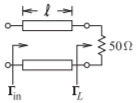
Figura\(\PageIndex{5}\)

1. ¿Cuál es el coeficiente de reflexión de modo diferencial\(\Gamma_{d}\),, a la carga?
2. ¿Qué hay\(\Gamma_{d}\) en la entrada de las líneas?

5.14.1 Ejercicios por Sección

\(†\)desafiante,\(‡\) muy desafiante

\(§5.2\: 1†\)

\(§5.5\: 2†, 3‡\)

\(§5.6\: 4, 5,\)

\(§5.8\: 6, 7, 8, 9†, 10†, 11, 12†, 13†, 14†, 15†, 16\)

\(§5.9\: 17, 18, 19, 20\)

\(§5.10\: 21, 22, 23, 24, 25, 26, 27\)

5.14.2 Respuestas a ejercicios seleccionados

2. (h)\(3.87\)

5. c)\(v_{po}=1.256\cdot 10^{8}\text{ m/s}\)
6. \(0.9950\)
7. b)\(187\text{ mW}\)

9. (e)\(D=10\text{ dB}\)
10. \(Z_{0e}=67.84\:\Omega\)

17. \(C=2\jmath /(Z_{0e}-Z_{0o})\)

21. \(32.5\:\Omega\)

24. \(0.4118\)

26. \(-0.0323\)