2.1: Introducción

Los filtros son los más fundamentales de los circuitos de procesamiento de señales que utilizan elementos de almacenamiento de energía para obtener características dependientes de la frecuencia. Algunos de los atributos de filtro importantes son (1) controlar el ruido al no permitir que el ruido fuera de banda se propague en un circuito; (2) evitar que las señales fuera de la banda de transmisión, especialmente los armónicos, se transmitan; y (3) presentar solo señales en una banda especificada a la circuitería de recepción activa. A frecuencias de microondas, un filtro puede consistir únicamente en elementos agrupados, únicamente de elementos distribuidos o una mezcla de elementos agrupados y distribuidos. Las realizaciones distribuidas pueden ser implementaciones basadas en líneas de transmisión de los componentes de prototipos de filtro de elementos agrupados o, preferiblemente, hacer uso de las características de frecuencia particulares encontradas con ciertas estructuras distribuidas. La pérdida de elementos agrupados, particularmente por encima de unos pocos gigahercios, significa que el rendimiento de los filtros distribuidos casi siempre supera al de los filtros de elementos agrupados. Sin embargo, dado que el componente básico de un filtro distribuido es una línea de transmisión de un cuarto de longitud de onda, los filtros distribuidos pueden ser prohibitivamente grandes por debajo de unos pocos gigahercios.

Solo se requieren unos pocos tipos básicos de respuestas de la mayoría de los filtros de RF de la siguiente manera:

1. Paso bajo: proporciona la máxima transferencia de potencia a frecuencias por debajo de la frecuencia de esquina,\(f_{0}\). Arriba\(f_{0}\), la transmisión está bloqueada. Véase la Figura\(\PageIndex{1}\) (a).
2. Paso alto: señales de paso alto a frecuencias superiores\(f_{0}\). Abajo\(f_{0}\), la transmisión está bloqueada. Ver Figura\(\PageIndex{1}\) (b).
3. Paso de banda: pasar señales en frecuencias entre frecuencias de esquina inferior y superior (definiendo la banda de paso) y bloqueando la transmisión fuera de la banda. Este es el tipo más común de filtro RF. Ver Figura\(\PageIndex{1}\) (c).
4. Bandstop (o notch): que bloquea las señales entre las frecuencias de esquina inferior y superior (definiendo la banda de detención). Ver Figura\(\PageIndex{1}\) (d).
5. Allpass: que ecualiza una señal ajustando la fase generalmente para corregir la distorsión de fase en otro lugar. Ver Figura\(\PageIndex{1}\) (e).

La lista anterior no es exhaustiva, ya que las condiciones reales de operación pueden exigir perfiles de frecuencia específicos. Por ejemplo, los sistemas WiFi que operan en\(2.45\text{ GHz}\) son susceptibles a que se transmitan señales potencialmente grandes desde teléfonos celulares cercanos que operan en el\(1700–2300\text{ MHz}\) rango. Por lo tanto, un filtro frontend para un\(2.45\text{ GHz}\) sistema debe garantizar niveles muy altos de atenuación en el\(1700–2300\text{ MHz}\) rango. Así, la solución óptima aquí, probablemente, tendrá una respuesta de frecuencia asimétrica con alto rechazo en un lado de la banda de paso obtenida al aceptar un rechazo menor en el otro lado.

2.1.1 Prototipos de filtros

En la década de 1960 se desarrolló un enfoque para el diseño y síntesis de filtros de RF y esto todavía se sigue. El enfoque es traducir la respuesta matemática de un filtro de paso bajo. Luego se sintetiza un filtro con la respuesta de paso bajo deseada usando elementos agrupados y el filtro resultante se denomina prototipo de paso bajo. El filtro de paso bajo se transforma entonces de modo que el nuevo filtro de elementos grumados tenga la respuesta de RF deseada, como paso alto o paso de banda. En el caso de un filtro de paso de banda, cada inductor y condensador del prototipo de paso bajo se convierte en un resonador que se acopla a otro resonador. En forma distribuida, este resonador básico es una línea de transmisión de un cuarto de longitud de onda.

La síntesis de filtros es un enfoque sistemático para realizar circuitos con características de frecuencia deseadas. Un filtro también puede pensarse como una implementación de hardware de una ecuación diferencial que produce un impulso específico,

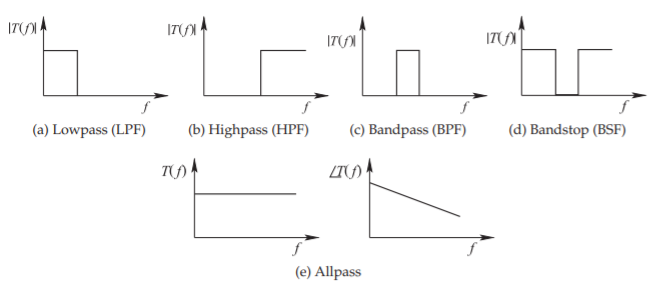
Figura\(\PageIndex{1}\): Función de transferencia de filtro ideal,\(T(f)\), respuestas.

paso, o respuesta de frecuencia. No es sorprendente que un filtro pueda describirse de esta manera como los elementos reactivos agrupados,\(L\) y\(C\), describir ecuaciones diferenciales de primer orden y su interconexión describe ecuaciones diferenciales de orden superior.

La síntesis de una respuesta de filtro comienza identificando la respuesta de ecuación diferencial deseada. Las ecuaciones diferenciales se especifican usando la variable Laplace,\(s\), de modo que en el dominio de frecuencia (con\(s =\jmath\omega\)) una ecuación diferencial de\(n\)\(n\) orden th se convierte en una expresión polinómica de orden th en\(s\). Si es posible, y este suele ser el caso, se puede desarrollar una versión de paso bajo de un filtro. La conversión a la forma final del filtro, digamos una respuesta de paso de banda, procede matemáticamente a través de varias etapas. Cada etapa tiene una forma de circuito y cada etapa se denomina prototipo de filtro.

2.1.2 Parámetros de imagen versus métodos de pérdida de inserción

Las redes de filtro se pueden sintetizar usando el método del parámetro de imagen o el método del coeficiente de reflexión (o pérdida de inserción) [1]. El parámetro de imagen medido se basa en redes en cascada de dos puertos con cada puerto teniendo la respuesta de filtro deseada esencial [2]. Varios de estos dos puertos están conectados en cascada para lograr una estructura periódica que tiene la respuesta de filtro final deseada. Este método es restrictivo y no se pueden obtener respuestas de filtro arbitrarias. Rara vez se utiliza en el diseño de filtros de RF y microondas pero es útil para analizar estructuras simples con cascadas de elementos idénticos [3]. Un mejor enfoque es utilizar el método de pérdida de inserción como se usa en este capítulo.