2.21: Ejercicios

Última actualización
Guardar como PDF

Page ID: 85154

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

La función característica de una red doblemente terminada es\(K(s) = s^{2}\).
1. ¿Cuál es el coeficiente de transmisión de magnitude-cuadrado\((|T (s)|^{2})\)?
2. ¿Cuál es el coeficiente de reflexión magnitude-cuadrado\((|\Gamma (s)|^{2})\)?
3. ¿Cuál es el coeficiente de transmisión\(T(s)\) para un circuito que se puede realizar usando positivo\(R,\: L,\) y\(C\) elementos)?
La función característica de una red doblemente terminada es\(K(s) = s^{4}\). ¿Cuál es el coeficiente de transmisión de magnitude-cuadrado\((|\Gamma (s)|^{2})\)?
Considere el diseño de un filtro Butterworth de paso bajo de cuarto orden. [Este problema sigue el desarrollo de la Sección 2.4.]
1. ¿Cuál es el polinomio característico de magnitud cuadrada,\(|K(s)|^{2}\), del filtro Butterworth?
2. ¿Cuál es el coeficiente de transmisión de magnitud-cuadrado (o función de transferencia)?
3. ¿Cuál es la función del coeficiente de reflexión de magnitude-cuadrado?
4. Derivar la función del coeficiente de reflexión (i.e.,\(\Gamma (s)\)). Anote el coeficiente de reflexión en forma factorizada utilizando hasta factores de segundo orden.
5. ¿Cuáles son las raíces del polinomio numerador de la función coeficiente de reflexión?
6. ¿Cuáles son las raíces del polinomio denominador de la función coeficiente de reflexión?
7. Identificar los pares de polos conjugados en el coeficiente de reflexión factorizado.
8. Trazar los polos y ceros del coeficiente de reflexión en el\(s\) plano complejo.
Derivar los polos de coeficiente de reflexión de un filtro Butterworth de segundo orden y escribir el coeficiente de reflexión con polinomios nominador y denominador, que no está en forma factorizada. [Ejemplo de Parallels 2.4.1]
Derivar el coeficiente de reflexión polos y ceros de un filtro Chebyshev de cuarto orden con un factor de ondulación,\(\varepsilon\), de\(0.1\).
Sintetizar la función de impedancia Es
\[Z_{x}=\frac{s^{3}+s^{2}+2s+1}{s^{2}+s+1}\nonumber \]
decir, desarrollar el\(RLC\) circuito que realiza\(Z_{x}\). [Ejemplo de Parallels 2.6.1]
Sintetizar la función de impedancia Es
\[Z_{w}=\frac{4s^{2}+2s+1}{8s^{3}+8s^{2}+2s+1}\nonumber \]
decir, desarrollar el\(RLC\) circuito que realiza\(Z_{w}\). [Ejemplo de Parallels 2.6.2]
Sintetizar la función de impedancia Es
\[Z_{x}=\frac{4s^{2}+2s+1}{4s^{2}+1}\nonumber \]
decir, desarrollar el\(RLC\) circuito que realiza\(Z_{x}\). [Parallels Ejemplo 2.6.1. También es posible que desee consultar la Figura 2.6.2.]
Sintetizar la función de impedancia Es
\[Z_{x}=\frac{4s^{4}+2s^{3}+5s^{2}+2s+1}{4s^{4}+4s^{3}+7s^{2}+s+1}\nonumber \]
decir, desarrollar el\(RLC\) circuito que realiza\(Z_{x}\). [Parallels Ejemplo 2.6.1. También es posible que desee consultar la Figura 2.6.2.]
Desarrolle el prototipo de paso bajo de un filtro de paso bajo Butterworth de quinto orden. Puede haber más de una solución. Es decir, dibujar el circuito del prototipo de filtro de paso bajo con valores de elementos.
Desarrolle el prototipo de paso bajo de un filtro de paso bajo Chebyshev de quinto orden con frecuencia de\(1\text{ dB}\) ondulación y\(1\text{ rad/s}\) esquina.
Desarrolle el prototipo de paso bajo de un filtro de paso bajo Chebyshev de nueve orden con frecuencia de\(0.01\text{ dB}\) ondulación y\(1\text{ rad/s}\) esquina.
Un inversor\(0.04\text{ S}\) de admitancia se implementará en microcinta usando una sola longitud de línea de transmisión. La permitividad efectiva de la línea es\(9\) y la frecuencia central de diseño es\(10\text{ GHz}\).
1. ¿Cuál es la impedancia característica de la línea de transmisión?
2. ¿Cuál es la longitud de onda en milímetros en la frecuencia central de diseño en el espacio libre?
3. ¿Cuál es la longitud de onda en milímetros en la frecuencia central de diseño en microcinta?
4. ¿Cuál es la longitud eléctrica de la línea de transmisión de microcinta en grados en la frecuencia central de diseño?
5. ¿Cuál es la longitud de la línea de transmisión de microcinta en milímetros?
En la Sección 2.8.2 se vio que un inductor en serie puede ser reemplazado por un condensador de derivación con inversores y un transformador de unidad negativa. Si el inversor se realiza con una línea de transmisión larga de un cuarto de longitud de onda de impedancia característica\(50\:\Omega\):
1. Derivar los\(ABCD\) parámetros de la cascada de la Figura 2.8.2 (c) con\(50\:\Omega\) inversores.
2. ¿Cuál es el valor de la capacitancia de derivación en la cascada requerida para realizar un\(1\text{ nH}\) inductor?
Un inductor en serie de\(10\text{ pH}\) debe ser realizado por un circuito equivalente usando condensadores de derivación y secciones de una línea de\(1\:\Omega\) transmisión de un cuarto de longitud de onda de longitud de onda. Diseñar el circuito equivalente. [Pista: Las líneas largas de un cuarto de longitud de onda son inversores de impedancia.]
Un inductor en serie de\(10\text{ nH}\) debe ser realizado por un circuito equivalente usando condensadores de derivación y secciones de una línea de\(50\:\Omega\) transmisión de un cuarto de longitud de onda de longitud de onda. [Pista: Las líneas largas de un cuarto de longitud de onda son inversores de impedancia.] Diseñar el circuito equivalente.
En\(5\text{ GHz}\), un\(5\text{ nH}\) inductor en serie debe realizarse usando uno o más inversores de\(75\:\Omega\) impedancia, un transformador de unidad y un condensador. ¿Cuál es el valor del condensador?
En la Sección 2.8.3 se vio que un condensador en serie puede ser reemplazado por un inductor de derivación con inversores y un transformador de unidad negativa. Considere que los inversores se realizan con una línea de transmisión de un cuarto de longitud de onda de longitud de onda de impedancia característica\(100\:\Omega\).
1. Derivar los\(ABCD\) parámetros de la cascada de la Figura 2.8.3 con\(100\:\Omega\) los inversores.
2. ¿Cuál es el valor de la inductancia de derivación en la cascada requerida para realizar un\(1\text{ pH}\) condensador?
Un inversor de\(50\:\Omega\) impedancia debe realizarse usando tres stubs resonantes. La frecuencia central del diseño es\(f_{0}\). La primera frecuencia resonante de los talones es\(f_{r} = 2f_{0}\).
1. Dibuja el circuito usando stubs. En su diagrama indica la impedancia de entrada y la impedancia característica de cada uno de los stubs si\(f_{r} = 2f_{0}\).
2. ¿Cuál es la impedancia de entrada de una línea de transmisión de longitud de onda corta de un octavo de longitud de onda si la impedancia característica de la línea es\(Z_{01}\)?
3. ¿Cuál es la impedancia de entrada de una transmisión larga de un octavo de longitud de onda abierta?
4. ¿Cuál es la impedancia de entrada de una transmisión corta de un octavo de longitud de onda larga si la impedancia característica de la línea es\(Z_{02}\)?
5. ¿Cuál es la longitud de cada uno de los stubs en el inversor en términos de la longitud de onda a la frecuencia\(f_{0}\)?
Diseñe un filtro de paso alto Type\(1\) Chebyshev de tercer orden con una frecuencia de esquina\(1\text{ GHz}\), una impedancia del\(50\:\Omega\) sistema y\(0.2\text{ dB}\) ondulación. Hay una serie de pasos en el diseño, y para demostrar que los entiendes se te pide que completes los diseños parciales que se indican a continuación. A continuación se muestra un prototipo de filtro de\(1\) paso bajo Cauer\(\omega_{c}\) siendo la frecuencia del radián de esquina,\(f_{c} = \omega_{c}/(2\pi )\) siendo la frecuencia de esquina y\(Z_{0}\) siendo la impedancia del sistema.

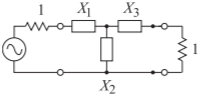
Figura\(\PageIndex{1}\)

Diseñar un LPF con\(\omega_{c} = 1\text{ rad/s}\),\(Z_{0} =1\:\Omega\).
Diseñar un HPF con\(\omega_{c} = 1\text{ rad/s}\),\(Z_{0} =1\:\Omega\).
Diseñar un HPF con\(f_{c} = 1\text{ GHz}\),\(Z_{0} =1\:\Omega\).
Diseñar un HPF con\(f_{c} = 1\text{ GHz}\),\(Z_{0} = 50\:\Omega\).

Este problema considera el diseño de un filtro de paso de banda Butterworth en\(900\text{ MHz}\).
1. Diseñar un filtro de paso bajo Butterworth de\(LC\) segundo orden con frecuencia de esquina\(1\text{ rad/s}\) en un\(1\:\Omega\) sistema.
2. Usando el prototipo de filtro anterior, diseñe un filtro de paso bajo con una frecuencia de esquina de\(900\text{ MHz}\).
3. Diseñe un filtro de paso de banda Butterworth de segundo orden\(900\text{ MHz}\) usando el prototipo de filtro de paso bajo en (a). Utilice un ancho de banda fraccional de\(0.1\) y una impedancia del sistema de\(50\:\Omega\).
4. ¿Cuál es el\(3\text{ dB}\) ancho de banda del filtro en (c)?
Diseñe un prototipo de filtro de paso de banda máximo plano de tercer orden en un\(50\:\Omega\) sistema centrado en\(1\text{ GHz}\) con un\(10\%\) ancho de banda. El prototipo de paso bajo de un filtro plano máximo de tercer orden se muestra en la Figura 2.6.3.
1. Convierta el filtro de paso bajo prototipo en un filtro de paso bajo con inversores y condensadores solamente; es decir, retire los inductores en serie.
2. Escala el filtro para tomar la frecuencia de esquina de\(1\text{ rad/s}\) a\(1\text{ GHz}\).
3. Transforme el filtro de paso bajo en un filtro de paso de banda. Es decir, reemplace cada condensador de derivación por una\(LC\) red paralela. Este paso establecerá el ancho de banda del filtro.
4. Transformar la impedancia del sistema del filtro de\(1\) a\(50\:\Omega\).
A continuación se muestra el prototipo de paso bajo de un filtro Butterworth de paso bajo de cuarto orden. La frecuencia de esquina es\(1\text{ rad/s}\).

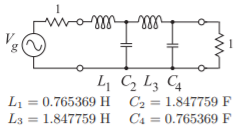
Figura\(\PageIndex{2}\)

Basado en esto, desarrollar un prototipo de filtro de paso de banda Butterworth de cuarto orden centrado en\(10^{9}\text{ rad/s}\) con un ancho de banda fraccional de\(5\%\).

Escala el prototipo de paso bajo para tener una frecuencia de esquina de\(10^{9}\text{ rad/s}\). Dibuja el prototipo con valores de elementos.
Dibuje el esquema del prototipo de paso de banda Butterworth de cuarto orden de elementos agrupados basado en el prototipo de filtro de paso bajo original.
Derivar los valores de los elementos del prototipo de filtro paso banda de elementos agrupados en un\(75\:\Omega\) sistema.

Diseñe un filtro de paso alto Type\(2\) Chebyshev de tercer orden con una frecuencia de esquina\(1\text{ GHz}\), una impedancia del\(50\:\Omega\) sistema y\(0.2\text{ dB}\) ondulación. Hay una serie de pasos en el diseño, y para demostrar que los entiendes se te pide que completes la tabla a continuación. Para cada etapa de la síntesis del filtro se debe indicar si el elemento es una inductancia o una capacitancia mediante escritura\(L\) o\(C\) en la celda correspondiente. Otras celdas requieren un valor numérico y se deben incluir unidades. El\(X\) elemento se identifica en el prototipo a continuación. Se muestra un prototipo de filtro de\(2\) paso bajo Cauer con ωc siendo la frecuencia del radián de esquina,\(f_{c} = \omega_{c}/(2\pi )\) siendo la frecuencia de esquina y\(Z_{0}\) siendo la impedancia del sistema.

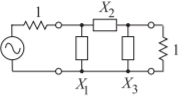
Figura\(\PageIndex{3}\)

Complete la columna LPF (filtro paso bajo) de la tabla con\(\omega_{c} = 1\text{ rad/s}\),\(Z_{0} =1\:\Omega\).
Completar la columna HPF (filtro paso alto) de la mesa con\(\omega_{c} = 1\text{ rad/s}\),\(Z_{0} =1\:\Omega\).
Completar la segunda columna HPF de la tabla con\(f_{c} = 1\text{ GHz}\),\(Z_{0} =1\:\Omega\).
Completar la tercera columna HPF de la tabla con\(f_{c} = 1\text{ GHz}\),\(Z_{0} = 50\:\Omega\).

ELEMENTO	LPF
	\(\omega_{c}=1\text{ rad/s}\),\(Z_{0}=1\:\Omega\)
	\(L\)o\(C\)	Valor (unidades)
\(X_{1}\)	\ (\ omega_ {c} =1\ texto {rad/s}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (\ omega_ {c} =1\ text {rad/s}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">
\(X_{2}\)	\ (\ omega_ {c} =1\ texto {rad/s}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (\ omega_ {c} =1\ text {rad/s}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">
\(X_{3}\)	\ (\ omega_ {c} =1\ texto {rad/s}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (\ omega_ {c} =1\ text {rad/s}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">

Mesa\(\PageIndex{1}\)

ELEMENTO	HPF
	\(\omega_{c}=1\text{ rad/s}\),\(Z_{0}=1\:\Omega\)
	\(L\)o\(C\)	Valor (unidades)
\(X_{1}\)	\ (\ omega_ {c} =1\ texto {rad/s}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (\ omega_ {c} =1\ text {rad/s}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">
\(X_{2}\)	\ (\ omega_ {c} =1\ texto {rad/s}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (\ omega_ {c} =1\ text {rad/s}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">
\(X_{3}\)	\ (\ omega_ {c} =1\ texto {rad/s}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (\ omega_ {c} =1\ text {rad/s}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">

Mesa\(\PageIndex{2}\)

ELEMENTO	HPF
	\(f_{c}=1\text{ GHz}\),\(Z_{0}=1\:\Omega\)
	\(L\)o\(C\)	Valor (unidades)
\(X_{1}\)	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">
\(X_{2}\)	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">
\(X_{3}\)	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=1\:\Omega\)\(L\) o\(C\) “>	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=1\:\Omega\) Valor (unidades) ">

Mesa\(\PageIndex{3}\)

ELEMENTO	HPF
	\(f_{c}=1\text{ GHz}\),\(Z_{0}=50\:\Omega\)
	\(L\)o\(C\)	Valor (unidades)
\(X_{1}\)	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=50\:\Omega\)\(L\) o\(C\) “>	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=50\:\Omega\) Valor (unidades) ">
\(X_{2}\)	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=50\:\Omega\)\(L\) o\(C\) “>	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=50\:\Omega\) Valor (unidades) ">
\(X_{3}\)	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=50\:\Omega\)\(L\) o\(C\) “>	\ (f_ {c} =1\ texto {GHz}\),\(Z_{0}=50\:\Omega\) Valor (unidades) ">

Mesa\(\PageIndex{4}\)

¿Cuál es la impedancia de entrada de una línea de transmisión\(\lambda /8\) larga en cortocircuito con una impedancia característica de\(Z_{0}\)?
¿Cuál es la impedancia de entrada de una línea de transmisión\(\lambda /8\) larga de circuito abierto con una impedancia característica de\(Z_{0}\)?
Aplicar la transformación de Richards a un inductor de derivación con una reactancia de\(50\:\Omega\). ¿Cuál es la longitud eléctrica del trozo cortocircuitado si el trozo tiene una impedancia característica de\(50\:\Omega\)?
Aplique la transformación de Richards a un condensador de derivación con una reactancia de\(−50\:\Omega\). ¿Cuál es la impedancia característica del trozo de circuito abierto si la longitud eléctrica del trozo es de un cuarto de longitud de onda?

2.12.1 Ejercicios por Sección

\(†\)desafiante,\(‡\) muy desafiante

\(§2.2\: 1†, 2\)

\(§2.4\: 3†, 4†\)

\(§2.5\: 5†\)

\(§2.6\: 6†, 7†, 8†, 9†\)

\(§2.7\: 10, 11†, 12†\)

\(§2.8\: 13, 14†, 15†, 16†, 17†, 18†, 19†\)

\(§2.9\: 20†, 21†, 2†2, 23†, 24†\)

\(§2.12\: 25, 26, 27†, 28†\)

2.12.2 Respuestas a ejercicios seleccionados

c)\(\Gamma(s)=\frac{s^{2}}{s^{2}+\sqrt{2}s+1}\)
\(|T(w)|^{2}=1/(1+\omega^{8})\)
f)\(\begin{array}{l}{−0.38 + \jmath 0.92} \\ {−0.38 -\jmath 0.92} \\ {−0.92 + \jmath 0.38} \\ {-0.38-\jmath 0.92}\end{array}\)

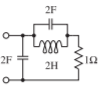
Figura\(\PageIndex{4}\)

c)\(9\)
(a)\(\left[\begin{array}{cc}{1}&{sC(50)^{2}}\\{0}&{1}\end{array}\right]\)

\(889\text{ fF}\)
\(10\text{ nH}\)
c)\(-Z_{2}=-\jmath 50\:\Omega\)

\(1\text{ GHz},\: 50\:\Omega,\: \text{HPF}: X_{3}=6.5\text{ nH}\)

Search

Text Color

Text Size

Margin Size

Font Type