Saltar al contenido principal
LibreTexts Español

6.14: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    85248

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    1. Un mezclador tiene un LO en\(28.2\text{ GHz}\). El mezclador se utiliza para convertir una señal at\(28.1\text{ GHz}\) a un IF at\(100\text{ MHz}\), y tiene una pérdida de conversión de\(13\text{ dB}\) y un rechazo de imagen de\(40\text{ dB}\). Dos señales se presentan al mezclador, una a\(28.1\text{ GHz}\) con una potencia de\(1\text{ pW}\) y la otra a\(28.3\text{ GHz}\) con una potencia de\(10\:\mu\text{W}\). [Ejemplo de Parallels 6.2.1]
      1. ¿Cuál es el poder de la señal (pretendida) en el IF en\(\text{dBm}\)?
      2. ¿Cuál es la relación señal/interferencia en el IF (ignorando el ruido)?
    2. Considere el mezclador de diodos de un solo extremo en la Figura 6.2.5 (a).
      1. Desarrollar una expresión simbólica para el voltaje en el punto de prueba. El diodo es modelado por\(i_{D} = a_{1}v_{D} + a_{2}v^{2}_{D} + a_{3}v^{3}_{D}\).
      2. ¿Cuáles son las frecuencias y amplitudes de los componentes del espectro en el punto de prueba?
    3. Un mezclador en un receptor tiene una pérdida de conversión de\(16\text{ dB}\). Si la señal de RF aplicada tiene una potencia disponible de\(100\:\mu\text{W}\), ¿cuál es la potencia disponible del IF en la salida del mezclador?
    4. La señal de RF aplicada a la entrada de un mezclador tiene una potencia de\(1\text{ nW}\) y la salida del mezclador en el IF tiene un nivel de potencia de\(100\text{ pW}\). ¿Cuál es la pérdida de conversión del mezclador en decibelios?
    5. Un mezclador en un receptor tiene una ganancia de conversión de\(10\text{ dB}\). Si la señal de RF aplicada tiene una potencia de\(100\:\mu\text{W}\), ¿cuál es la potencia disponible del IF en la salida del mezclador?
    6. Un mezclador en un receptor tiene una pérdida de conversión de\(6\text{ dB}\). Si la señal de RF aplicada tiene una potencia de\(1\:\mu\text{W}\), ¿cuál es la potencia disponible del IF en la salida del mezclador?
    7. Un mezclador tiene un LO en\(18\text{ GHz}\). El mezclador se utiliza para convertir una señal at\(18.5\text{ GHz}\) a una IF at\(500\text{ MHz}\). Se presentan dos señales al mezclador, una a\(18.5\text{ GHz}\) con una potencia de\(100\text{ nW}\) y una señal interferente\(17.5\text{ GHz}\) con una potencia de\(10\text{ nW}\). Si el rechazo de imagen es\(20\text{ dB}\) y la pérdida de conversión es\(10\text{ dB}\).
      1. ¿Cuál es la potencia de la señal en el IF?
      2. ¿Cuál es el poder de interferencia en el IF?
      3. ¿Cuál es la relación señal/interferencia (en decibelios) en el IF?
    8. Un mezclador tiene un LO en\(100\text{ GHz}\). El mezclador se utiliza para convertir una señal at\(110\text{ GHz}\) a una IF at\(10\text{ GHz}\). Se presentan dos señales al mezclador, una a\(110\text{ GHz}\) con una potencia de\(10\text{ nW}\) y una señal interferente\(90\text{ GHz}\) con una potencia de\(5\text{ nW}\). Si el rechazo de imagen es\(40\text{ dB}\) y la pérdida de conversión es\(20\text{ dB}\), ¿cuál es la relación señal/interferencia (en decibelios) en el IF?
    9. Un mezclador tiene un LO en\(18\text{ GHz}\). El mezclador se utiliza para convertir una señal at\(18.5\text{ GHz}\) a una IF at\(500\text{ MHz}\). La señal de RF en\(18.5\text{ GHz}\) tiene una potencia de\(100\text{ pW}\). Además, el ruido con una potencia de\(1\text{ pW}\) se aplica al mezclador en\(18.5\text{ GHz}\) y\(17.5\text{ GHz}\) (\(1\text{ pW}\)at\(18.5\text{ GHz}\) y\(1\text{ pW}\) at\(17.5\text{ GHz}\)). Si el rechazo de imagen es\(6\text{ dB}\) y la pérdida de conversión es\(10\text{ dB}\). Ignorar las contribuciones de ruido del mezclador. ¿Qué es el SNR (en decibelios) en el IF?
    10. Un mezclador en un sistema de comunicación tiene un LO en\(5.5\text{ GHz}\). El mezclador se utiliza para convertir una señal de\(10\text{ MHz}\) ancho de banda\(5.6\text{ GHz}\) a un IF at\(100\text{ MHz}\). La señal de RF en\(5.6\text{ GHz}\) tiene una potencia de\(100\text{ pW}\). El rechazo de imagen es ideal y la pérdida de conversión lo es\(10\text{ dB}\). El mezclador tiene una figura de ruido de banda lateral única de\(6\text{ dB}\).
      1. ¿Cuál es la potencia de ruido en la entrada si la fuente se mantiene a temperatura estándar (\(290\text{ K}\))?
      2. ¿Cuál es la SNR de entrada (en decibelios)?
      3. ¿Qué es el SNR (en decibelios) en el IF?
    11. El mezclador de diodos de anillo de doble equilibrado que se muestra a continuación tiene la característica especial de que los tonos LO y RF se suprimen en el puerto de salida IF. Desarrollar una expresión simbólica para el voltaje en el puerto IF. Los diodos están emparejados y son modelados por\(i_{D} = a_{1}v_{D} + a_{2}v^{2}_{D} + a_{3}v^{3}_{D}\). El voltaje LO, en el terminal LO, es\(v_{\text{LO}} = A \cos(\omega_{\text{LO}}t)\) y el voltaje RF, en el terminal RF, es\(v_{\text{RF}} = B \cos(\omega_{\text{RF}}t)\). Considera una relación de\(1:1\) bobinado. Es decir, el número de devanados en el secundario a cada lado del grifo central es igual al número de devanados en el primario.

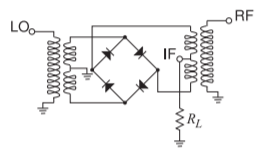
    clipboard_e065d040c0e59f55ecae96db116f497e2.png

    1. Un mezclador de doble equilibrio de diodo tiene un LO en\(100\text{ GHz}\) y tiene una señal de RF de entrada de\(101\text{ GHz}\). ¿Cuáles serán las frecuencias de las señales principales en el IF?
    2. El ruido de fase de un oscilador se midió como\(−120\text{ dBc/Hz}\) en\(10\text{ kHz}\) offset. ¿Cuál es el ruido de fase normalizado en\(1\text{ MHz}\) offset, suponiendo que la potencia del ruido de fase varía como la inversa de la frecuencia?
    3. El ruido de fase de un oscilador se midió como\(−130\text{ dBc/Hz}\) en\(10\text{ kHz}\) offset. ¿Cuál es el ruido de fase normalizado en\(1\text{ MHz}\) offset, suponiendo que la potencia del ruido de fase varía como la inversa de la frecuencia?
    4. El ruido de fase de un oscilador se midió como\(−125\text{ dBc/Hz}\) en\(100\text{ kHz}\) offset. ¿Cuál es el ruido de fase normalizado en\(1\text{ MHz}\) offset, suponiendo que la potencia del ruido de fase varía como el cuadrado de la inversa de frecuencia?
    5. El ruido de fase de un oscilador se midió como\(−125\text{ dBc/Hz}\) en\(100\text{ kHz}\) offset. ¿Cuál es el ruido de fase normalizado en\(1\text{ MHz}\) offset, suponiendo que la potencia del ruido de fase varía inversamente con el desplazamiento de frecuencia?
    6. Cuando\(0\text{ V}\) se aplica a un VCO, la frecuencia de salida es\(1\text{ GHz}\). Cuando la entrada al VCO es\(10\text{ mV}\), la salida sinusoidal del VCO tiene una frecuencia de\(1.01\text{ GHz}\). ¿Cuál es la ganancia de afinación del VCO?
    7. Si se aplica un voltaje sinusoidal a la entrada de un VCO analógico, describa la señal en la salida del VCO.
    8. Describir el diseño de un divisor de frecuencia de dos tiempos utilizando un multiplicador de frecuencia basado en un diodo y uno o más filtros pasabanda. Es decir, esbozar el circuito a nivel de diagrama de bloques.
    9. Describir el diseño de un divisor de frecuencia de tres tiempos utilizando un multiplicador de frecuencia basado en un diodo y uno o más filtros pasabanda. Es decir, esbozar el circuito a nivel de diagrama de bloques.

    6.14.1 Ejercicios Por Sección

    \(†\)desafiante,\(‡\) muy desafiante

    \(§6.2 1, 2†, 3, 4, 5, 6, 7†, 8†, 9†, 10†\)

    \(§6.3 11‡, 12\)

    \(§6.4 13†, 14†, 15†, 16\)

    \(§6.5 17, 18\)

    \(§6.9 19, 20\)

    6.14.2 Respuestas a ejercicios seleccionados

    1. \(-26\text{ dBm}\)
    1. \(0\text{ dBm}\)
    1. b)\(10\text{ pW}\)
    1. \(19.0\text{ dB}\)
    2. b)\(28\text{ dB}\)
    1. Una señal en\(1\text{ GHz}\)
    1. \(1\text{ GHz/V}\)

    6.14: Ejercicios is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.