2.6: Extracción de elementos

En las dos secciones anteriores se derivaron las respuestas matemáticas de los filtros Butterworth y Chebyshev para diversos órdenes. En esta sección se mostrará cómo estos filtros se pueden implementar con inductores y capacitores utilizando lo que se denomina síntesis en escalera [4].

2.6.1 Síntesis en Escalera

Para obtener los valores de los elementos que producen la función de transferencia deseada, primero se debe obtener una función de impedancia o admitancia. La función de impedancia o admitancia se puede obtener fácilmente a partir del coeficiente de reflexión de entrada de una red, pero por ahora el foco está en sintetizar una función de impedancia dada. Una función de impedancia general se puede expresar como

$$\label{eq:1}Z(s)=\frac{a_{n}(s^{2} +\omega_{1}^{2})(s^{2} + \omega_{3}^{2})(s^{2} + \omega_{5}^{2})\cdots}{b_{m}s (s^{2} +\omega_{2}^{2}) (s^{2} + \omega_{4}^{2}) (s^{2} +\omega_{6}^{2})\cdots}$$

donde$a_{n}$ y$b_{m}$ son constantes. Esto se puede realizar usando$L$ y$C$ elementos en una red terminada por una resistencia, siempre que el grado del numerador y denominador difieran en no más que la unidad (es decir,$|m−n|\leq 1$). En

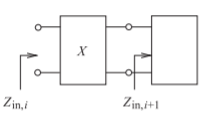
Figura$\PageIndex{1}$: Extracción de una red$X$ para reducir una impedancia$Z_{\text{in, }i}$ a una impedancia de orden inferior$Z_{\text{in, }i+1}$.

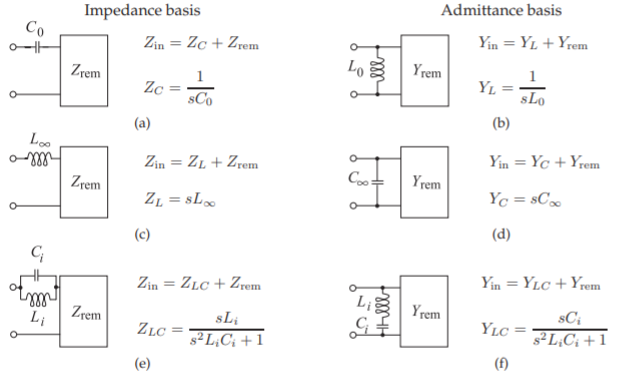
Figura$\PageIndex{2}$: Síntesis de funciones de impedancia y admitancia. Comenzando con una función de impedancia$Z(s)$: (a) extracción de un condensador en serie; (c) extracción de un inductor en serie; y (e) extracción de un$LC$ bloque paralelo en serie$i$. Comenzando con una función de admitancia$Y(s)$: (b) extracción de un inductor de derivación; (d) extracción de un condensador de derivación; y (f) extracción de un$LC$ bloque en serie de derivación.

el caso de una red doblemente terminada, esta resistencia es la carga. El procedimiento de extracción de elementos, mostrado en la Figura$\PageIndex{1}$, implica extraer una red$X$ de$Z_{\text{in, }i}$, dejando una impedancia de orden reducido$Z_{\text{in, }i+1}$.

La extracción de inductores y capacitores se ilustra en la Figura$\PageIndex{2}$. Así, tras la extracción de un elemento o de un par de elementos queda una impedancia$Z_{\text{rem}}$, o admitancia$Y_{\text{rem}}$, que puede simplificarse de manera similar. Por ejemplo, y haciendo referencia a la Figura$\PageIndex{2}$ (a),$Z(s)=1/(sC)+Z_{\text{rem}}$. Entonces un polo de$Z(s)$ a CC requiere la extracción de un condensador en serie de valor (ver Figura$\PageIndex{2}$ (a))

$$\label{eq:2}C_{0}=\left.\frac{1}{sZ(s)}\right|_{s=0}$$

mientras que un polo en el infinito requiere la extracción de un inductor de valor en serie (ver Figura$\PageIndex{2}$ (c))

$$\label{eq:3}L_{\infty}=\left.\frac{Z(s)}{s}\right|_{s=\infty}$$

Otra posibilidad es un polo a una frecuencia finita (llamarlo así$\omega_{0}$), que requiere la extracción de un$LC$ bloque paralelo en serie, como se muestra en la Figura$\PageIndex{2}$ (e), con elementos de valor

$$\label{eq:4}C_{i}=\left.\frac{s}{(s^{2}+\omega_{2}^{2})Z(s)}\right|_{s=\jmath\omega_{0}}\quad\text{and}\quad L_{i}=\frac{1}{\omega_{0}^{2}C_{i}}$$

El proceso de extracción también se puede llevar a cabo sobre una base de admisión. Primero

$$\label{eq:5}Y(s)=\frac{b_{m}s (s^{2} +\omega_{2}^{2})(s^{2} +\omega_{4}^{2})(s^{2} + \omega_{s}^{2})\cdots}{a_{n} (s^{2} +\omega_{1}^{2}) (s^{2} +\omega_{3}^{2}) (s^{2} +\omega_{5}^{2})\cdots}$$

Ahora un polo a cero requiere la extracción de un inductor de derivación de valor (ver Figura$\PageIndex{2}$ (b))

$$\label{eq:6}L_{0}=\left.\frac{1}{sY(s)}\right|_{s=0}$$

y un polo en el infinito requiere la extracción de un condensador de derivación de valor (ver Figura$\PageIndex{2}$ (d))

$$\label{eq:7}C_{\infty}=\left.\frac{Y(s)}{s}\right|_{s=\infty}$$

Un polo a una frecuencia finita requiere la extracción de un$LC$ bloque de la serie shunt (como se muestra en la Figura$\PageIndex{2}$ (f)) con valores

$$\label{eq:8}L_{i}=\left.\frac{s}{(s^{2}+\omega_{0}^{2})Y(s)}\right|_{s=\jmath\omega_{0}}\quad\text{and}\quad C_{i}=\frac{1}{\omega_{0}^{2}L_{i}}$$

Muchos aspectos de la síntesis de filtros pueden parecer abstractos cuando se presentan en plena generalidad. En consecuencia, es común ilustrar conceptos de síntesis de filtros usando ejemplos. Siguiendo esta tradición consagrada, ahora se presenta un ejemplo.

Ejemplo$\PageIndex{1}$: Element Extraction for a Third-Order Lowpass Filter

Un filtro plano máximo de tercer orden tiene el coeficiente de reflexión

$$\label{eq:9}\Gamma_{1}(s)=\frac{s^{3}}{(s+1)(s^{2}+s+1)}$$

Sintetizar este filtro como una red doblemente terminada.

Solución

La función coeficiente de reflexión (Ecuación$\eqref{eq:9}$) tiene todos sus polos ubicados en el infinito, por lo que la realización de la red correspondiente debe estar hecha de simples$L$ o$C$ elementos y terminada en una resistencia. Por lo tanto, haciendo referencia a la Figura 2.2.1 y considerando un$1\:\Omega$ sistema,

$$\label{eq:10}Z_{\text{in, }1}(s)=\frac{1+\Gamma_{1}(s)}{1-\Gamma_{1}(s)}=\frac{2s^{3}+2s^{2}+2s+1}{2s^{2}+2s+1}$$

Tenga en cuenta que la impedancia de entrada se acerca al infinito ya que la frecuencia va al infinito, de ahí que se deba extraer un inductor en serie. El valor de este inductor es

$$\label{eq:11}L_{\infty 1}=\left.\frac{Z_{\text{in, }1}(s)}{s}\right|_{s=\infty}=1\text{ H}$$

El filtro se desarrolla extrayendo un elemento a la vez. Después de la extracción del primer elemento, se deja la impedancia de la segunda etapa. Ahora la función de impedancia es

$$\begin{aligned} Z_{\text{in, }2}(s)&=Z_{\text{in, }1}(s)-sL_{\infty 1}=\frac{2s^{3}+2s^{2}+2s+1}{2s^{2}+2s+1}-sL_{\infty 1} \\ &=\frac{2s^{3}+2s^{2}+2s+1-s(2s^{2}+2s+1)}{2s^{2}+2s+1}=\frac{s+1}{2s^{2}+2s+1}\end{aligned}\nonumber$$

Tenga en cuenta que la impedancia de etapa anterior,$Z_{\text{in, }2}$, se acerca a cero a medida que la frecuencia va al infinito. No hay un solo elemento de serie que provoque esto. Sin embargo, la función de admisión de etapa,

$$\label{eq:12}Y_{\text{in, }2}(s)=\frac{1}{Z_{\text{in, }2}(s)}=\frac{2s^{2}+2s+1}{s+1}$$

va al infinito a medida que la frecuencia se acerca al infinito y así se extrae un condensador de derivación:

$$\label{eq:13}Y_{\text{in, }3}(s)=Y_{\text{in, }2}(s)-sC_{\infty 2}=\frac{1}{s+1}$$

donde

$$\label{eq:14}C_{\infty 2}=2F$$

Entonces a veces es más conveniente considerar la extracción de una admitancia y a veces es mejor considerar la extracción de una impedancia.

Al examinar la impedancia de etapa restante, se ve que existe un polo en el infinito, y así se extrae un inductor en serie$L_{\infty 3}$,,. El valor de este inductor proviene de

$$\label{eq:15}Z_{\text{in, }3}=\frac{1}{Y_{\text{in, }3}}=s+1\:\Omega$$

y así el valor del inductor es

$$\label{eq:16}L_{\infty 3}=\left.\frac{s+1}{s}\right|_{S=\infty}=1\text{ H}$$

El paso final es extraer una carga de valor 1 de la siguiente manera:

$$\label{eq:17}Z_{\text{in, }4}=Z_{\text{in, }s}-sL_{\infty 3}=1\:\Omega$$

Este ejemplo sintetizó una red doblemente terminada. La red resultante, llamada circuito de escalera, se muestra en la Figura$\PageIndex{3}$. La$1\:\Omega$ resistencia más a la izquierda es parte de la fuente.

Este circuito tiene una forma dual que consiste en dos condensadores de derivación separados por un inductor en serie. El circuito dual deriva de realizar la función de admitancia obtenida a partir del coeficiente de reflexión. Otras técnicas de extracción de red se presentan en Scanlan y Levy [4, 5] y Matthaei et al. [1].

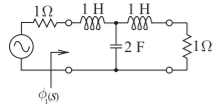
Figura$\PageIndex{3}$: Red sintetizada máximamente plana con una respuesta de reflexión de paso bajo de tercer orden.

2.6.2 Resumen

La función de impedancia de entrada de un circuito de elementos agrupados siempre se puede expresar como la relación de dos polinomios en$s$ y el orden del numerador y los polinomios denominador pueden diferir como máximo en uno [5]. Si los órdenes difieren en uno, entonces siempre se puede extraer un solo inductor o condensador, sin embargo, la función de impedancia restante puede no ser realizable. Esto indica que se requiere una combinación más compleja$LC$ (y posiblemente$R$). Para poder extraer sistemáticamente circuitos complejos arbitrariamente, se requiere una larga lista de posibles funciones, como las que se muestran en la Figura$\PageIndex{2}$. Para la mayoría de los circuitos de interés las$LC$ combinaciones mostradas en la Figura$\PageIndex{2}$ son suficientes. El siguiente ejemplo describe la extracción de función de impedancia que requiere una$LC$ combinación.

Ejemplo$\PageIndex{2}$: Element Extraction of an Impedance Function

Realice la función de impedancia$Z_{w}=\frac{4s^{3}+4s^{2}+2s+2}{4s^{2}+2s+1}$.

Solución

El orden del numerador es$1$ mayor que el orden del denominador y esto indica que quizás esté presente un inductor en serie. La inductancia en serie es

$$\label{eq:18} L_{1}=\left.\frac{Z_{w}(s)}{(s)}\right|_{z=\infty}=1\text{ H}$$

La impedancia restante es

$$\label{eq:19}Z_{\text{in, }2}=Z_{w}-sL_{1}=\frac{4s^{3}+4s^{2}+2s+2}{4s^{2}+2s+1}-s=\frac{2s^{2}+s+2}{4s^{2}+2s+1}$$

El numerador y denominador de$Z_{\text{in, }2}$ tienen el mismo orden. Por lo tanto, no se puede utilizar un$C$ elemento simple$L$ o para reducir la complejidad de la función de impedancia. Por lo tanto, un inductor de serie inicial no fue la elección correcta y la extracción debe retroceder.

La figura$\PageIndex{2}$ muestra varias combinaciones de elementos que se pueden utilizar para reducir la complejidad de una función de impedancia. Insight en qué alternativa elegir proviene de la factorización$z_{w}$, y tenga en cuenta que se requieren raíces reales, por lo tanto

$$\label{eq:20}Z_{w}=\frac{4s^{3}+4s^{2}+2s+2}{4s^{2}+2s+1}=\frac{(2s^{2}+1)(2s+2)}{4s^{2}+2s+1}$$

El examen de la Figura$\PageIndex{2}$ revela que no$Z_{w}$ se encuentra un ajuste listo para. En su lugar, considere la función de admisión

$$\label{eq:21}Y_{w}=\frac{1}{Z_{w}}=\frac{4s^{2}+2s+1}{(2s^{2}+1)(2s+2)}$$

Entonces, la reducción que se muestra en la Figura$\PageIndex{2}$ (f) parece el candidato adecuado. La elección general para el elemento es

$$\label{eq:22}y_{x}=\frac{as}{bs^{2}+1}$$

Elegir$b = 2$ ahora reduce la complejidad (ya que parte del denominador factorizado de$Y_{w}$ ahora ocurre), entonces

$$\begin{align}\label{eq:23}Y_{w}&=\frac{as}{2s^{2}+1}+\left(\frac{4s^{2}+2s+1}{(2s^{2}+1)(2s+2)}-\frac{as}{2s^{2}+1}\right) \\ \label{eq:24}&=\frac{as}{2s^{2}+1}+\left(\frac{(4-2a)s^{2}+(2-2a)s+1}{(2s^{2}+1)(2s+2)}\right)\end{align}$$

Elija$a = 1$,

$$\begin{align}\label{eq:25}Y_{w}&=\frac{s}{(2s^{2}+1)}+\frac{2s^{2}+1}{(2s^{2}+1)(2s+2)}=\frac{s}{2s^{2}+1}+\frac{1}{2s+2} \\ \label{eq:26}&=\frac{s}{2s^{2}+1}+Y_{\text{in, }2}\end{align}$$

Entonces$C_{1}L_{1} = b = 1,\: C_{1} = a = 1\text{ F},\: L_{1} = 2\text{ H}$, y

$$\label{eq:27}Y_{\text{in, }2}=\frac{1}{(2s+2)}\quad\text{or}\quad Z_{\text{in, }2}=\frac{1}{Y_{\text{in, }2}}=2s+2$$

La red final es

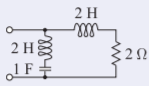
Figura$\PageIndex{4}$