3.8: Ejercicios

Ejercicio 3.1

Dejar\([P]\) ser la matriz de transición para una cadena de Markov de estado finito y dejar que el estado\(i\) sea recurrente. Demostrar que\(i\) es aperiódico si\(P_{i i}>0\).

Ejercicio 3.2

Demostrar que cada cadena de Markov con\( \mathrm{M}<\infty\) estados contiene al menos un conjunto recurrente de estados. Es suficiente explicar cada una de las siguientes afirmaciones.

1. Si el estado\(i_{1}\) es transitorio, entonces hay algún otro estado\(i_{2}\) tal que\(i_{1} \rightarrow i_{2}\) y\(i_{2} \not \rightarrow i_{1}\).
2. Si el\(i_{2}\) de la parte a) también es transitoria, existe\(i_{3}\) tal que\(i_{2} \rightarrow i_{3}\),\(i_{3} \not \rightarrow i_{2}\), y consecuentemente\(i_{1} \rightarrow i_{3}\),\(i_{3} \not \rightarrow i_{1}\).
3. Continuando inductivamente, si también\(i_{k}\) es transitorio, hay\(i_{k+1}\) tal que\(i_{j} \rightarrow i_{k+1}\) y\(i_{k+1} \not \rightarrow i_{j}\) para\(1 \leq j \leq k\).
4. Demostrar que para algunos\(k \leq \mathbf{M}\), no\(k\) es transitorio, es decir, es recurrente, por lo que existe una clase recurrente.

Ejercicio 3.3

Consideremos una cadena de Markov de estado finito en la que algún estado dado, digamos el estado 1, sea accesible desde cualquier otro estado. Demostrar que la cadena tiene como máximo una clase recurrente\(\mathcal{R}\) de estados y estado\(1 \in \mathcal{R}\). (Tenga en cuenta que, combinado con el Ejercicio 3.2, hay exactamente una clase recurrente y la cadena es entonces una unicaína).

Ejercicio 3.4

Mostrar cómo generalizar la gráfica de la Figura 3.4 a un número arbitrario de estados\(\mathrm{M} \geq 3\) con un ciclo de M nodos y uno de M − 1 nodos. Para M = 4, deje que el nodo 1 sea el nodo que no esté en el ciclo de M − 1 nodos. Enumere el conjunto de estados accesibles desde el nodo 1 en\(n\) pasos para cada uno\(n \leq 12\) y muestre que el límite en el Teorema 3.2.4 se cumple con igualdad. Explicar por qué se mantiene el mismo resultado para todas las M más grandes

Ejercicio 3.5 (Prueba de Teorema 3.2.4)

1. Demostrar que una cadena ergódica de Markov con M estados debe contener un ciclo con\(\tau<\mathrm{M}\) estados. Pista: Use ergodicidad para mostrar que el ciclo más pequeño no puede contener M estados.
2. Dejar\(\ell\) ser un estado fijo en este ciclo de duración\(\tau\). \(\mathcal{T}(m)\)Sea el conjunto de estados accesibles desde\(\ell\) en\(m\) pasos. Demostrar que para cada uno\(m \geq 1\),\(\mathcal{T}(m) \subseteq \mathcal{T}(m+\tau)\). Pista: Para cualquier estado dado\(j \in \mathcal{T}(m)\), mostrar cómo construir un paseo de\(m+\tau\) pasos desde\(\ell\) hasta\(j\) desde el supuesto paseo de\(m\) pasos.
3. \(\mathcal{T}(0)\)Definir para ser el conjunto singleton\(\{i\}\) y mostrar que

   \(\mathcal{T}(0) \subseteq \mathcal{T}(\tau) \subseteq \mathcal{T}(2 \tau) \subseteq \cdots \subseteq \mathcal{T}(n \tau) \subseteq \cdots.\)

4. Demostrar que si una de las inclusiones anteriores está satisfecha con la igualdad, entonces todas las inclusiones posteriores se sacifican con la igualdad. Demuestre a partir de esto que a lo sumo las primeras\(M −1\) inclusiones pueden satisfacerse con una estricta desigualdad y eso\(\mathcal{T}(n \tau)=\mathcal{T}((M-1) \tau) \text { for all } n \geq M-1\).
5. Demostrar que todos los estados están incluidos en\(\mathcal{T}((M-1) \tau)\).
6. \(P_{i j}^{(\mathrm{M}-1)^{2}+1}>0\)Demuéstralo para todos\(i, j\).

Ejercicio 3.6

Consideremos una cadena de Markov con una clase ergódica de\(m\) estados, digamos\(\{1,2, \ldots, m\}\) y\(\mathrm{M}-m\) otros estados que son todos transitorios. Demuestre que\(P_{i j}^{n}>0\) para todos\(j \leq m\) y\(n \geq(m-1)^{2}+1+\mathrm{M}-m\)

Ejercicio 3.7

1. \(\tau\)Sea el número de estados en el ciclo más pequeño de una cadena de\(\mathrm{M} \geq 3\) estados ergódica arbitraria de Markov. \(P_{i j}^{n}>0\)Demuéstralo para todos\(n \geq(\mathrm{M}-2) \tau+\mathrm{M}\). Pista: Mira la prueba del Teorema 3.2.4 en el Ejercicio 3.5.
2. Para\(\tau=1\), dibujar la gráfica de una cadena ergódica de Markov (generalizada por arbitraria\(\mathrm{M} \geq 3\)) para la que hay una\(i\),\(j\) para la cual\(P_{i j}^{n}=0\) para\(n=2 \mathrm{M}-3\). Pista: Mira la Figura 3.4.
3. Por arbitrario\(\tau<\mathrm{M}-1\), dibujar la gráfica de una cadena ergódica de Markov (generalizada para M arbitraria) para la cual hay una\(i\),\(j\) para la cual\(P_{i j}^{n}=0\) para\(n=(\mathrm{M}-2) \tau+\mathrm{M}-1\).

Ejercicio 3.8

Se dice que una matriz de probabilidad de transición\([P]\) es doblemente estocástica si

\(\sum_{j} P_{i j}=1 \quad \text { for all } i ;\quad \sum_{i} P_{i j}=1 \quad \text { for all } j\)

Es decir, la suma de fila y la suma de columna son iguales cada una a 1. Si una cadena doblemente estocástica tiene M estados y es ergódica (es decir, tiene una sola clase de estados y es aperiódica), calcule sus probabilidades de estado estacionario.

Ejercicio 3.9

1. Encuentre las probabilidades de estado estacionario\(\pi_{0}, \ldots, \pi_{k-1}\) para la cadena Markov a continuación. Exprese su respuesta en términos de la proporción\(\rho=p / q\). Preste especial atención al caso especial\(\rho=1\).
2. Sketch\(\pi_{0}, \ldots, \pi_{k-1}\). Da un boceto para\(\rho=1 / 2\), uno para\(\rho=1\) y otro para\(\rho=2\).
3. Encuentra el límite de\(\pi_{0}\) como\(k\) enfoques\(\infty\); dar respuestas separadas para\(\rho<1\),\(\rho=1\), y\(\rho>1\). Encuentra valores limitantes de\(\pi_{k-1}\) para los mismos casos.

   

Ejercicio 3.10

1. Encuentre las probabilidades de estado estacionario para cada una de las cadenas de Markov en la Figura 3.2. Supongamos que todas las probabilidades en el sentido de las agujas del reloj en la primera gráfica son las mismas\(p\), digamos, y supongamos que\(P_{4,5}=P_{4,1}\) en la segunda gráfica.
2. Encuentra las matrices\([P]^{2}\) para las mismas cadenas. Dibuje las gráficas para las cadenas de Markov representadas por\([P]^{2}\), es decir, la gráfica de transiciones de dos pasos para las cadenas originales. Encuentra las probabilidades de estado estacionario para estas cadenas de dos pasos. Explica por qué tus probabilidades de estado estacionario no son únicas.
3. Encuentra\(\lim _{n \rightarrow \infty}\left[P^{2 n}\right]\) para cada una de las cadenas.

Ejercicio 3.11

1. Supongamos que\(\boldsymbol{\nu}^{(i)}\) es un vector propio derecho y\(\boldsymbol{\pi}^{(j)}\) es un vector propio izquierdo de una matriz estocástica M por M\([P]\) donde\(\lambda_{i} \neq \lambda_{j}\). \(\boldsymbol{\pi}^{(j)} \boldsymbol{\nu}^{(i)}=0\)Demuéstralo. Pista: Considera dos formas de encontrar\(\boldsymbol{\pi}^{(j)}[P] \boldsymbol{\nu}^{(i)}\).
2. Supongamos que\([P]\) tiene M valores propios distintos. Los vectores propios derechos de\([P]\) entonces abarcan el espacio M (ver sección 5.2 de Strang, [19]), por lo que la matriz\([U]\) con esos vectores propios como columnas no es singular. Mostrar que\(U^{-1}\) es un matix cuyas filas son los M vectores propios izquierdos de\([P]\). Pista: usa la parte a).
3. Para cada uno\(i\), deja\(\left[\Lambda^{(i)}\right]\) ser una matriz diagonal con un solo elemento distinto de cero,\(\left[\Lambda_{i i}^{(i)}\right]=\lambda_{i}\). Asumir eso\(\boldsymbol{\pi}_{i} \boldsymbol{\nu}_{k}=0\). Demostrar que

   \(\boldsymbol{\nu}^{(j)}\left[\Lambda^{(i)}\right] \boldsymbol{\pi}^{(k)}=\lambda_{i} \delta_{i k} \delta_{j k},\)

   donde\(\delta_{i k}\) es 1 si\(i=k\) y 0 en caso contrario. Pista visualizar directa vector/multiplicación matricial.

4. Verificar (3.30).

Ejercicio 3.12

1. Dejar\(\lambda_{k}\) ser un valor propio de una matriz estocástica\([P]\) y dejar\(\boldsymbol{\pi}^{(k)}\) ser un autovector para\(\lambda_{k}\). Demostrar que para cada componente\(\pi_{j}^{(k)}\) de\(\boldsymbol{\pi}^{(k)}\) y cada uno\(n\) que

   \(\lambda_{k}^{n} \pi_{j}^{(k)}=\sum_{i} \pi_{i}^{(k)} P_{i j}^{n}.\)

2. Al tomar magnitudes de cada lado, demuestra que

   \(\left|\lambda_{k}\right|^{n}\left|\pi_{j}^{(k)}\right| \leq \mathrm{M}.\)

3. \(\left|\lambda_{k}\right| \leq 1\)Demuéstralo.

Ejercicio 3.13

Considere una cadena de Markov de estado finito con matriz\([P]\) que tiene clases recurrentes\(\kappa\) aperiódicas,\(\mathcal{R}_{1}, \ldots, \mathcal{R}_{\kappa}\) y un conjunto\(\mathcal{T}\) de estados transitorios. Para cualquier clase recurrente dada\(\ell\), considere un vector\(\boldsymbol{\nu}\) tal que\(\nu_{i}=1\) para cada uno\(i \in \mathcal{R}_{\ell}\),\(\nu_{i}=\lim _{n \rightarrow \infty} \operatorname{Pr}\left\{X_{n} \in \mathcal{R}_{\ell} \mid X_{0}=i\right\}\) para cada uno\(i \in \mathcal{T}\), y de\(\nu_{i}=0\) otra manera. Mostrar que\(\boldsymbol{\nu}\) es un vector propio derecho de\([P]\) con valor propio 1. Pista: Redibuje la Figura 3.5 para múltiples clases recurrentes y primero muestre que\(\nu\) es un vector propio de\(\left[P^{n}\right]\) en el límite.

Ejercicio 3.14

Responde las siguientes preguntas para la siguiente matriz estocástica\([P]\)

\ ([P] =\ left [\ begin {array} {ccc}
1/2 & 1/2 & 0\\
0 & 1/2 & 1/2/2\
0 & 0 & 0 & 1
\ end {array}\ derecha].\)

1. Encuentra\([P]^{n}\) en forma cerrada por arbitrario\(n>1\).
2. Encuentra todos los valores propios distintos y la multiplicidad de cada valor propio distinto para\([P]\).
3. Encuentre un vector propio correcto para cada valor propio distinto y muestre que el valor propio de multiplicidad 2 no tiene 2 vectores propios linealmente independientes.
4. Usa\ ref {c} para mostrar que no hay matriz diagonal\([\Lambda]\) y ninguna matriz invertible\([U]\) para la cual\([P][U]=[U][\Lambda]\).
5. Rederivar el resultado de la parte d) usando el resultado de a) en lugar de c).

Ejercicio 3.15

1. Dejar\(\left[J_{i}\right]\) ser un bloque de 3 por 3 de una forma Jordan, es decir,

   \ (\ left [J_ {i}\ right] =\ left [\ begin {array} {ccc}
   \ lambda_ {i} & 1 & 0\\
   0 &\ lambda_ {i} & 1\\
   0 &\ lambda_ {i}
   \ end {array}\ right]\)

   Demostrar que el poder\(n\) th de\(\left[J_{i}\right]\) es dado por

   \ (\ left [J_ {i} ^ {n}\ right] =\ left [\ begin {array} {ccc}
   \ lambda_ {i} ^ {n} & n\ lambda_ {1} ^ {n-1} &\ left (\ begin {array} {c}
   n\\
   2
   \ end {array}\ derecha)\ lambda_ {i} ^ {n-1}\\ &
   0\ lambda_ {i} ^ {n} & n\ lambda_ {1} ^ {n-1}\ \
   0 & 0 &\ lambda_ {i} ^ {n}
   \ end {array}\ derecha]\)

   Pista: Quizás la forma más fácil es calcular\(\left[J_{i}^{2}\right]\)\(\left[J_{i}^{3}\right]\) y luego usar iteración.

2. Generalizar a) a a\(k\) por\(k\) bloque de una forma Jordan. Tenga en cuenta que el poder\(n\) th de toda una forma de Jordania está compuesto por estos bloques a lo largo de la diagonal de la matriz.
3. Dejar\([P]\) ser una matriz estocástica representada por una forma Jordan\([J]\) como\([P]=U^{-1}[J][U]\) y considerar\([U][P]\left[U^{-1}\right]=[J]\). Demostrar que cualquier valor propio repetido de\([P]\) (es decir, cualquier valor propio representado por un bloque Jordan de 2 por 2 o más) debe ser estrictamente inferior a 1. Pista: Límite superior de los elementos de\([U]\left[P^{n}\right]\left[U^{-1}\right]\) tomando la magnitud de los elementos de\([U]\) y\(\left[U^{-1}\right]\) y delimitando superior cada elemento de una matriz estocástica por 1.
4. Dejar\(\lambda_{s}\) ser el valor propio de mayor magnitud menor que 1. Supongamos que los bloques Jordan para\(\lambda_{s}\) son como máximo de tamaño\(k\). Demostrar que cada clase ergódica de\([P]\) converge al menos tan rápido como\(n^{k} \lambda_{s}^{k}\).

Ejercicio 3.16

1. Dejar\(\lambda\) ser un valor propio de una matriz\([A]\), y let\(\nu\) y\(\boldsymbol{\pi}\) ser vectores propios derecha e izquierda respectivamente de\(\lambda\), normalizado de manera que\(\boldsymbol{\pi} \boldsymbol{\nu}=1\). Demostrar que

   \([[A]-\lambda \nu \boldsymbol{\pi}]^{2}=\left[A^{2}\right]-\lambda^{2} \boldsymbol{\nu} \boldsymbol{\pi}\)

2. \(\left[\left[A^{n}\right]-\lambda^{n} \boldsymbol{\nu} \boldsymbol{\pi}\right][[A]-\lambda \nu \boldsymbol{\pi}]=\left[A^{n+1}\right]-\lambda^{n+1} \boldsymbol{\nu} \boldsymbol{\pi}\)Demuéstralo.
3. Usa la inducción para demostrarlo\([[A]-\lambda \boldsymbol{\nu} \boldsymbol{\pi}]^{n}=\left[A^{n}\right]-\lambda^{n} \boldsymbol{\nu} \boldsymbol{\pi}\).

Ejercicio 3.17

\([P]\)Sea la matriz de transición para una unicadena aperiódica de Markov con los estados numerados como en la Figura 3.5.

1. Mostrar que\(\left[P^{n}\right]\) se puede particionar como

   \ (\ izquierda [P^ {n}\ derecha] =\ izquierda [\ begin {array} {cc}
   {\ izquierda [P_ {\ mathcal {T}} ^ {n}\ derecha]} & {\ izquierda [P_ {x} ^ {n}\ derecha]}\\
   0 & {\ izquierda [P_ {\ mathcal {R}} ^ {n}\ derecha]}
   \ final {array}\ derecho]\)

   Es decir, los bloques en la diagonal son simplemente productos de los bloques correspondientes de\([P]\), y el bloque superior derecho es lo que resulte ser.

2. \(q_{i}\)Sea la probabilidad de que la cadena esté en un estado recurrente después de\(t\) las transiciones, comenzando desde el estado i, es decir,\(q_{i}=\sum_{t<j \leq t+r} P_{i j}^{t}\). Demuestre eso\(q_{i}>0\) para todos los transitorios\(i\).
3. Dejar\(q\) ser el mínimo\(q_{i}\) sobre todos los transitorios\(i\) y mostrar que\(P_{i j}^{n t} \leq(1-q)^{n}\) para todos los transitorios\(i, j\) (es decir, mostrar que\(\left[P_{\mathcal{T}}\right]^{n}\) se acerca a la matriz todo cero\([0]\) con el aumento\(n\)).
4. Dejar\(\boldsymbol{\pi}=\left(\boldsymbol{\pi}_{\mathcal{T}}, \boldsymbol{\pi}_{\mathcal{R}}\right)\) ser un vector propio izquierdo de\([P]\) de valor propio 1. \(\boldsymbol{\pi}_{\mathcal{R}}\)Demostrar eso\(\pi_{\mathcal{T}}=0\) y mostrar que debe ser positivo y ser un vector propio izquierdo de\(\left[P_{\mathcal{R}}\right]\). Así muestran que\(\boldsymbol{\pi}\) existe y es único (dentro de un factor de escala).
5. Mostrar que\(\boldsymbol{e}\) es el vector propio derecho único\([P]\) de valor propio 1 (dentro de un factor de escala).

Ejercicio 3.18

Generalizar el Ejercicio 3.17 al caso de una cadena de Markov\([P]\) con clases\(m\) recurrentes y una o más clases transitorias. En particular,

1. Mostrar que\([P]\) tiene vectores propios izquierdos exactamente\(\kappa\) linealmente independientes,\(\boldsymbol{\pi}^{(1)}, \boldsymbol{\pi}^{(2)}, \ldots, \boldsymbol{\pi}^{(\kappa)}\) de valor propio 1, y que el\(m\) th se puede tomar como un vector de probabilidad que es positivo en la clase recurrente\(m\) th y cero en otra parte.
2. Mostrar que\([P]\) tiene exactamente vectores propios derechos\(\kappa\) linealmente independientes,\(\boldsymbol{\nu}^{(1)}, \boldsymbol{\nu}^{(2)}, \ldots, \boldsymbol{\nu}^{(\kappa)}\) de valor propio 1, y que el mth se puede tomar como un vector con\(\nu_{i}^{(m)}\) igual a la probabilidad de que la clase recurrente alguna vez\(m\) sea ingresada a partir del estado\(i\).
3. Demostrar que

   \(\lim _{n \rightarrow \infty}\left[P^{n}\right]=\sum_{m} \boldsymbol{\nu}^{(m)} \boldsymbol{\pi}^{(m)}\).

Ejercicio 3.19

Supongamos que una cadena recurrente de Markov tiene periodo\(d\) y deja\(\mathcal{S}_{m}, 1 \leq m \leq d\), ser el subconjunto\(m\) th en el sentido del Teorema 3.2.3. Supongamos que los estados están numerados de manera que\(s_{1}\) los primeros estados son los estados de\(\mathcal{S}_{1}\), los siguientes\(s_{2}\) son los de\(\mathcal{S}_{2}\), y así sucesivamente. Así, la matriz\([P]\) para la cadena tiene la forma de bloque dada por

\ ([P] =\ izquierda [\ begin {array} {ccccc}
0 & {\ izquierda [P_ {1}\ derecha]} &\ ddots &\ ddots &\
ddots & 0\\ 0 & 0 & {\ izquierda [P_ {2}\ derecha]} &
\ ddots &\ ddots\\ ddots &\ ddots &\ ddots\ &
0 &\ ddots & ;\ ddots & {\ left [P_ {d-1}\ derecha]}\\
{\ izquierda [P_ {d}\ derecha]} & 0 &\ ddots &\ ddots &\ ddots & 0
\ end {array}\ derecha],\)

donde\(\left[P_{m}\right]\) tiene dimensión\(s_{m}\) por\(s_{m+1}\) para\(1 \leq m \leq d\), donde\(d+1\) se interpreta como 1 a lo largo. En lo que sigue suele ser más conveniente expresarse\(\left[P_{m}\right]\) como una matriz M por M\(\left[P_{m}^{\prime}\right]\) cuyas entradas son 0 excepto por las filas de\(\mathcal{S}_{m}\) y las columnas de\(\mathcal{S}_{m+1}\), donde las entradas son iguales a las de\(\left[P_{m}\right]\). En este punto de vista,\([P]=\sum_{m=1}^{d}\left[P_{m}^{\prime}\right]\).

1. Demostrar que\(\left[P^{d}\right]\) tiene la forma

   \ (\ izquierda [P^ {d}\ derecha] =\ izquierda [\ begin {array} {cccc}
   {\ izquierda [Q_ {1}\ derecha]} & 0 &\ ddots & 0\\
   0 & {\ izquierda [Q_ {2}\ derecha]} &\ ddots &\ ddots\\
   0 & 0 &\ ddots & {\ izquierda [Q_ {d}\ derecha]}
   \ end {array}\ derecha],\)

   donde\(\left[Q_{m}\right]=\left[P_{m}\right]\left[P_{m+1}\right] \ldots\left[P_{d}\right]\left[P_{1}\right] \ldots\left[P_{m-1}\right]\). Expresando\(\left[Q_{m}\right]\) como una matriz M por M\(\left[Q_{m}^{\prime}\right]\) cuyas entradas son 0 excepto para las filas y columnas de\(\mathcal{S}_{m}\) donde las entradas son iguales a las de\(\left[Q_{m}\right]\), esto se vuelve\(\left[P^{d}\right]=\sum_{m=1}^{d} Q_{m}^{\prime}\).

2. Mostrar que\(\left[Q_{m}\right]\) es la matriz de una cadena ergódica de Markov, de manera que con los vectores propios\(\hat{\boldsymbol{\pi}}_{m}, \hat{\boldsymbol{\nu}}_{m}\) como se define en el Ejercicio 3.18,\(\lim _{n \rightarrow \infty}\left[P^{n d}\right]=\sum_{m=1}^{d} \hat{\boldsymbol{\nu}}^{(m)} \hat{\boldsymbol{\pi}}^{(m)}\).
3. \(\hat{\boldsymbol{\pi}}^{(m)}\left[P_{m}^{\prime}\right]=\hat{\boldsymbol{\pi}}^{(m+1)}\)Demuéstralo. Tenga en cuenta que\(\hat{\boldsymbol{\pi}}^{(m)}\) es una M-tupla que es distinta de cero solo en los componentes de\(\mathcal{S}_{m}\).
4. Dejar\(\phi=\frac{2 \pi \sqrt{-1}}{d}\) y dejar\(\boldsymbol{\pi}^{(k)}=\sum_{m=1}^{d} \hat{\boldsymbol{\pi}}^{(m)} e^{m k \phi}\). Mostrar que\(\boldsymbol{\pi}^{(k)}\) es un vector propio izquierdo de\([P]\) de valor propio\(e^{-\phi k}\).

Ejercicio (continuación de Exerciese 3.19)

1. Demostrar que, con los vectores propios definidos en los Ejercicios 3.19,

   \(\lim _{n \rightarrow \infty}\left[P^{n d}\right][P]=\sum_{i=1}^{d} \boldsymbol{\nu}^{(i)} \boldsymbol{\pi}^{(i+1)},\)

   donde, como antes,\(d+1\) se toma como 1.

2. Demostrar que, para\(1 \leq j<d\),

   \(\lim _{n \rightarrow \infty}\left[P^{n d}\right]\left[P^{j}\right]=\sum_{i=1}^{d} \boldsymbol{\nu}^{(i)} \boldsymbol{\pi}^{(i+j)}\).

3. Demostrar que

   \(\lim _{n \rightarrow \infty}\left[P^{n d}\right]\left\{I+[P]+\ldots,\left[P^{d-1}\right]\right\}=\left(\sum_{i=1}^{d} \boldsymbol{\nu}^{(i)}\right)\left(\sum_{i=1}^{d} \boldsymbol{\pi}^{(i+j)}\right)\).

4. Demostrar que

   \(\lim _{n \rightarrow \infty} \frac{1}{d}\left(\left[P^{n}\right]+\left[P^{n+1}\right]+\cdots+\left[P^{n+d-1}\right]\right)=e \pi\),

   donde\(\boldsymbol{\pi}\) es el vector de probabilidad de estado estacionario para\([P]\). Pista: Demuestre eso\(\boldsymbol{e}=\sum_{m} \boldsymbol{\nu}^{(m)}\) y\(\boldsymbol{\pi}=(1 / d) \sum_{m} \boldsymbol{\pi}^{(m)}\).

5. Demostrar que el resultado anterior también es válido para unichains periódicos.

Ejercicio 3.21

Supongamos\(A\) y\(B\) son cada una de las cadenas ergódicas de Markov con probabilidades de transición\(\left\{P_{A_{i}, A_{j}}\right\}\) y\(\left\{P_{B_{i}, B_{j}}\right\}\) respectivamente. Denotar las probabilidades de estado estacionario de\(A\) y\(B\) por\(\left\{\pi_{A_{i}}\right\}\) y\(\left\{\pi_{B_{i}}\right\}\) respectivamente. Las cadenas ahora están conectadas y modificadas como se muestra a continuación. En particular, los estados\(A_{1}\) y ahora\(B_{1}\) están conectados y las nuevas probabilidades de transición\(P^{\prime}\) para la cadena combinada están dadas por

\ (\ begin {array} {lll}
P_ {A_ {1}, B_ {1}} ^ {\ prime} & =\ varepsilon,\ quad P_ {A_ {1}, A_ {j}} ^ {\ prime} =( 1-\ varepsilon) P_ {A_ {1}, A_ {j}} &\ texto {para todos} A_ {j}\\
P_ {B_ {1}, A_ {1}} ^ {\ prime} &=\ delta,\ quad P_ {B_ {1}, B_ {j}} ^ {\ prime} =( 1-\ delta) P_ {B_ {1}, B_ {j}} &\ texto {para todos} B_ {j}
\ end {array}\)

Todas las demás probabilidades de transición siguen siendo las mismas. Piensa intuitivamente en\(\varepsilon\) y\(\delta\) como siendo pequeño, pero no hagas ninguna aproximación en lo que sigue. Dé sus respuestas a las siguientes preguntas como funciones de\(\varepsilon, \delta,\left\{\pi_{A_{i}}\right\} \text { and }\left\{\pi_{B_{i}}\right\}\).

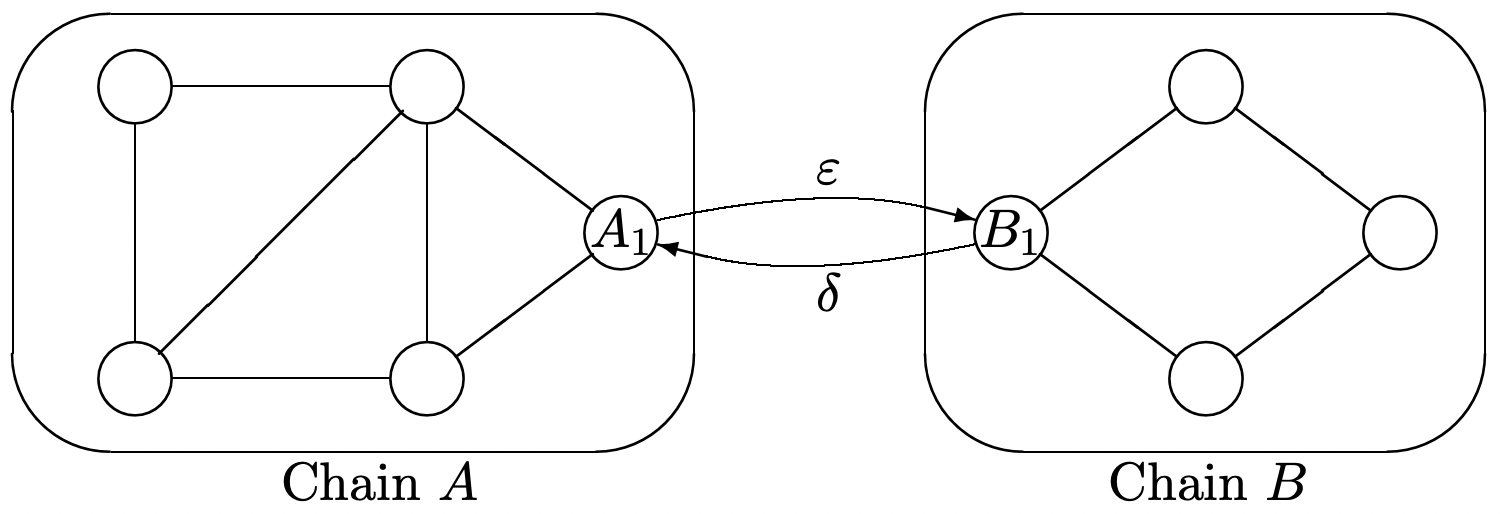
1. Supongamos que\(\epsilon>0, \delta=0\), (es decir, que\(A\) es un conjunto de estados transitorios en la cadena combinada). Comenzando en estado\(A_{1}\), encuentra el tiempo condicional esperado para regresar\(A_{1}\) dado que la primera transición es a algún estado en cadena\(A\).
2. Asumir eso\(\epsilon>0, \delta=0\). Encontrar\(T_{A, B}\), el tiempo esperado para llegar primero al estado\(B_{1}\), a partir del estado\(A_{1}\). Su respuesta debe ser una función de\(\epsilon\) y las probabilidades originales de estado estacionario\(\left\{\pi A_{i}\right\}\) en cadena\(A\).
3. Asumir\(\varepsilon>0, \delta>0\)\(T_{B, A}\), encontrar, el tiempo esperado para llegar primero al estado\(A_{1}\), comenzando en estado\(B_{1}\). Tu respuesta debe depender únicamente de\(\delta\) y\(\left\{\pi_{B_{i}}\right\}\).
4. Asumir\(\varepsilon>0\) y\(\delta>0\). Encontrar\(P^{\prime}(A)\), la probabilidad en estado estacionario de que la cadena combinada se encuentre en uno de los estados\(\left\{A_{j}\right\}\) de la cadena original\(A\).
5. Asumir\(\varepsilon>0, \delta=0\). Para cada estado\(A_{j} \neq A_{1}\) en\(A\), encontrar\(v_{A_{j}}\), el número esperado de visitas a estado\(A_{j}\), iniciando en estado\(A_{1}\), antes de llegar a estado\(B_{1}\). Tu respuesta debe depender únicamente de\(\varepsilon\) y\(\left\{\pi_{A_{i}}\right\}\).
6. Asumir\(\varepsilon>0, \delta>0\). Para cada estado\(A_{j}\) en\(A\), encontrar\(\pi_{A_{j}}^{\prime}\), la probabilidad de estado estacionario de estar en estado\(A_{j}\) en la cadena combinada. Pista: Tenga cuidado en su tratamiento del estado\(A_{1}\).

Ejercicio 3.22

El ejemplo 3.5.1 mostró cómo encontrar los tiempos esperados de primer paso a un estado fijo, digamos 1, de todos los demás nodos. A menudo es deseable incluir el primer tiempo de recurrencia esperado desde el estado 1 para regresar al estado 1. Esto se puede hacer dividiendo el estado 1 en 2 estados, primero un estado inicial sin transiciones entrando en él pero las transiciones originales saliendo, y segundo, un estado de captura final con las transiciones originales entrando.

1. Para la cadena del lado izquierdo de la Figura 3.6, dibuje la gráfica para la cadena modificada con 5 estados donde el estado 1 se ha dividido en 2 estados.
2. Supongamos que uno ha encontrado los tiempos esperados de primer paso\(v_{j}\) para estados\(j=2\) a 4 (o en general de 2 a M). Encontrar una expresión para\(v_{1}\), el primer tiempo de recurrencia esperado para el estado 1 en términos de\(v_{2}, v_{3}, \ldots v_{\mathrm{M}}\) y\(P_{12}, \ldots, P_{1 \mathrm{M}}\).

Ejercicio 3.23

1. Supongamos a lo largo de eso\([P]\) es la matriz de transición de una unicadena (y así el valor propio 1 tiene multiplicidad 1). Mostrar que\([P] \boldsymbol{w}-\boldsymbol{w}=\boldsymbol{r}-g\boldsymbol{e}\) existe una solución a la ecuación si y sólo si\(\boldsymbol{r}-g\boldsymbol{e}\) yace en el espacio de columna de\([P-I]\) donde\(I\) está la matriz de identidad.
2. Mostrar que este espacio de columna es el conjunto de vectores\(\boldsymbol{x}\) para los cuales\(\boldsymbol{\pi} \boldsymbol{x}=0\). Entonces muestra que\(\boldsymbol{r}-g \boldsymbol{e}\) se encuentra en este espacio de columna.
3. Demostrar que, con la restricción extra de que\(\boldsymbol{\pi} \boldsymbol{w}=0\), la ecuación\([P] \boldsymbol{w}-\boldsymbol{w}=\boldsymbol{r}-g \boldsymbol{e}\) tiene una solución única.

Ejercicio 3.24

Para la cadena Markov con recompensas en la Figura 3.7,

1. Encuentra la solución a (3.5.1) y encuentra la ganancia\(g\).
2. Modifique la Figura 3.7 dejando\(P_{12}\) ser una probabilidad arbitraria. Encontrar\(g\) y\(\boldsymbol{w}\) otra vez y dar una explicación intuitiva de por qué\(P_{12}\) los efectos\(w_{2}\).

Ejercicio 3.25 (Prueba de Corolario 3.5.1)

1. Demostrar que la ganancia por etapa\(g\) es 0. Pista: Mostrar que\(\boldsymbol{r}\) es cero donde el vector de estado estacionario\(\boldsymbol{\pi}\) es distinto de cero.
2. Dejar\(\left[P_{\mathcal{R}}\right]\) ser la matriz de transición para los estados recurrentes y dejar\(\boldsymbol{r}_{\mathcal{R}}=0\) ser el vector de recompensa y\(\boldsymbol{w}_{\mathcal{R}}\) el vector de ganancia relativa para\(\left[P_{\mathcal{R}}\right]\). \(\boldsymbol{w}_{\mathcal{R}}=0\)Demuéstralo. Pista: Usar Teorema 3.5.1.
3. \(w_{i}=0\)Demuéstralo para todos\(i \in \mathcal{R}\). Pista: Compare las ecuaciones de ganancia relativa\([P]\) con las de\(\left[P_{\mathcal{R}}\right]\).
4. Demuéstralo para cada uno\(n \geq 0,\left[P^{n}\right] \boldsymbol{w}=\left[P^{n+1}\right] \boldsymbol{w}+\left[P^{n}\right] \boldsymbol{r}\). Pista: Comience con la ecuación de ganancia relativa para\([P] \).
5. \(\boldsymbol{w}=\left[P^{n+1}\right] \boldsymbol{w}+\sum_{m=0}^{n}\left[P^{m}\right] \boldsymbol{r}\)Demuéstralo. Pista: Suma el resultado en b).
6. Mostrar que\(\lim _{n \rightarrow \infty}\left[P^{n+1}\right] \boldsymbol{w}=0\) y que\(\lim _{n \rightarrow \infty} \sum_{m=0}^{n}\left[P^{m}\right] \boldsymbol{r}\) es finito, no negativo, y tiene componentes positivos para\(r_{i}>0\). Pista: Use lemma 3.3.3.
7. Demostrar el resultado final del corolario utilizando los resultados anteriores en\(\boldsymbol{r}=\boldsymbol{r}^{\prime}-\boldsymbol{r}^{\prime \prime}\).

Ejercicio 3.26

Considere la cadena Markov a continuación:

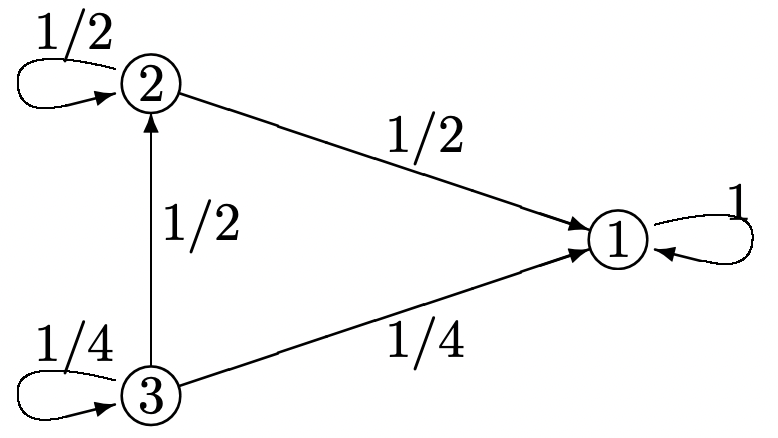
1. Supongamos que la cadena se inicia en estado\(i\) y pasa por n transiciones; deja\(v_{i}(n)\) ser el número esperado de transiciones (del total de\(n\)) hasta que la cadena entre en el estado de captura, estado 1. Encuentra una expresión para\(\boldsymbol{v}(n)=\left(v_{1}(n), v_{2}(n), v_{3}(n)\right)^{\top}\) en términos de\(\boldsymbol{v}(n-1)\) (tomar\(v_{1}(n)=0\) para todos\(n\)). (Pista: ver el sistema como un sistema de recompensas de Markov; ¿cuál es el valor de\(\boldsymbol{r}\)?)
2. Resolver numéricamente para\(\lim _{n \rightarrow \infty} \boldsymbol{v}(n)\). Interpretar el significado de los elementos\(v_{i}\) en la solución de (3.32).
3. Dar un argumento directo por qué\ ref {3.32} proporciona la solución directamente al tiempo esperado de cada estado para ingresar al estado de captura.

Ejercicio 3.27

1. Mostrar que\ ref {3.48} se puede reescribir en la forma más compacta

   \(\boldsymbol{v}^{*}(n, \boldsymbol{u})=\boldsymbol{v}^{*}\left(1, \boldsymbol{v}^{*}(n-1, \boldsymbol{u})\right)\).

2. Explique por qué también es cierto que

   \[\boldsymbol{v}^{*}(2 n, \boldsymbol{u})=\boldsymbol{v}^{*}\left(n, \boldsymbol{v}^{*}(n, \boldsymbol{u})\right).\label{3.65} \]

3. Uno podría adivinar que\ ref {3.65} podría usarse iterativamente, encontrando\(\boldsymbol{v}^{*}\left(2^{n+1}, \boldsymbol{u}\right)\) de\(\boldsymbol{v}^{*}\left(2^{n}, \boldsymbol{u}\right)\). Explique por qué esto no es posible de ninguna manera directa. Pista: Piense explícitamente cómo se podría calcular\(\boldsymbol{v}^{*}\left(n, \boldsymbol{v}^{*}(n, \boldsymbol{u})\right)\) a partir de\(\boldsymbol{v}^{*}(n, \boldsymbol{u})\).

Ejercicio 3.28

Considere una secuencia de rv binarios IID\(X_{1}, X_{2}, \ldots\) Supongamos que\(\operatorname{Pr}\left\{X_{i}=1\right\}=p_1\),\(\operatorname{Pr}\left\{X_{i}=0\right\}=p_{0}=1-p_{1}\). Una cadena binaria\(\left(a_{1}, a_{2}, \ldots, a_{k}\right)\) ocurre en el momento\(n\) si\(X_{n}=a_{k}, X_{n-1}=a_{k-1}, \ldots X_{n-k+1}=a_{1}\). Para una cadena dada\(\left(a_{1}, a_{2}, \ldots, a_{k}\right)\), considere una cadena de Markov con\(k+1\) estados\(\{0,1, \ldots, k\}\). Estado 0 es el estado inicial, estado\(k\) es un estado de captura final donde\(\left(a_{1}, a_{2}, \ldots, a_{k}\right)\) ya ocurrió, y cada estado interviniente\(i\),\(0<i<k\), tiene la propiedad de que si las\(k-i\) variables posteriores toman los valores\(a_{i+1}, a_{i+2}, \ldots, a_{k}\), la cadena de Markov se moverá sucesivamente desde estado\(i\)\(i+1\) a\(i+2\) y así sucesivamente a\(k\). Por ejemplo, si\(k=2\) y\(\left(a_{1}, a_{2}\right)=(0,1)\), la cadena correspondiente viene dada por

1. Para la cadena anterior, encuentra el tiempo medio de primer paso del estado 0 al estado 2.
2. Para las partes b) a d), let\(\left(a_{1}, a_{2}, a_{3}, \ldots, a_{k}\right)=(0,1,1, \ldots, 1)\), es decir, cero seguido de\(k-1\) unas. Dibuja la cadena de Markov correspondiente para\(k = 4\).
3. Que\(v_{i}\),\(1 \leq i \leq k\) sea el tiempo esperado de primer paso de estado\(i\) a estado\(k\). Tenga en cuenta que\(v_{k}=0\). \(v_{0}=1 / p_{0}+v_{1}\)Demuéstralo.
4. Para cada uno\(i\)\(1 \leq i<k\),, mostrar eso\(v_{i}=\alpha_{i}+v_{i+1}\) y\(v_{0}=\beta_{i}+v_{i+1}\) dónde\(\alpha_{i}\) y\(\beta_{i}\) son cada uno un producto de poderes de\(p_{0}\) y\(p_{1}\). Pista: usar inducción, o iteración, comenzando con\(i=1\), y establecer ambas igualdades juntas.
5. Dejar\(k=3\) y dejar\(\left(a_{1}, a_{2}, a_{3}\right)=(1,0,1)\). Dibuja la cadena de Markov correspondiente para esta cuerda. Evaluar\(v_{0}\), el tiempo esperado de primer paso para que ocurra la cadena 1,0,1.

Ejercicio 3.29

1. Encuentra\(\lim _{n \rightarrow \infty}\left[P^{n}\right]\) para la cadena Markov a continuación. Pista: Piense en términos de las probabilidades de transición a largo plazo. Recordemos que los bordes en la gráfica para una cadena de Markov corresponden a las probabilidades de transición positiva.
2. Dejar\(\boldsymbol{\pi}^{(1)}\) y\(\boldsymbol{\pi}^{(2)}\) denotar las dos primeras filas de\(\lim _{n \rightarrow \infty}\left[P^{n}\right]\) y let\(\boldsymbol{\nu}^{(1)}\) y\(\boldsymbol{\nu}^{(2)}\) denotar las dos primeras columnas de\(\lim _{n \rightarrow \infty}\left[P^{n}\right]\). Mostrar que\(\boldsymbol{\pi}^{(1)}\) y\(\boldsymbol{\pi}^{(2)}\) son vectores propios izquierdos independientes de\([P]\), y que\(\boldsymbol{\nu}^{(1)}\) y\(\boldsymbol{\nu}^{(2)}\) son vectores propios derechos independientes de\([P]\). Encuentra el valor propio para cada vector propio.

   

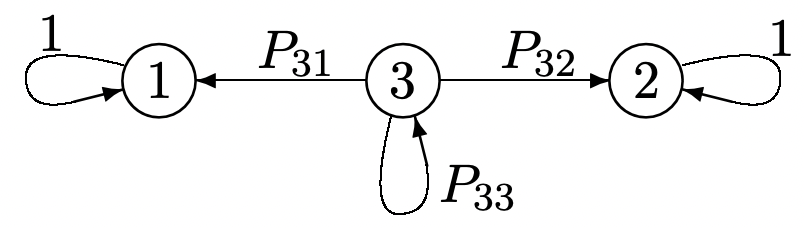
3. Dejar\(\boldsymbol{r}\) ser un vector de recompensa arbitrario y considerar la ecuación

   \[\boldsymbol{w}+g^{(1)} \boldsymbol{\nu}^{(1)}+g^{(2)} \boldsymbol{\nu}^{(2)}=\boldsymbol{r}+[P] \boldsymbol{w}\label{3.66} \]

   Determinar qué valores\(g^{(1)}\) y\(g^{(2)}\) deben tener para que\ ref {3.66} tenga una solución. Argumentan que con las restricciones adicionales\(w_{1}=w_{2}=0\),\ ref {3.66} tiene una solución única para\(\boldsymbol{w}\) y encuentra eso\(\boldsymbol{w}\).

Ejercicio 3.30

Dejar\(\boldsymbol{u}\) y\(\boldsymbol{u}^{\prime}\) ser vectores de recompensa final arbitrarios con\(\boldsymbol{u} \leq \boldsymbol{u}^{\prime}\).

1. Que\(\boldsymbol{k}\) sea una política estacionaria arbitraria y demuestre eso\(\boldsymbol{v}^{k}(n, \boldsymbol{u}) \leq \boldsymbol{v}^{k}\left(n, \boldsymbol{u}^{\prime}\right)\) para cada uno\(n \geq 1\).
2. Para la política dinámica óptima, demuéstralo\(\boldsymbol{v}^{*}(n, \boldsymbol{u}) \leq \boldsymbol{v}^{*}\left(n, \boldsymbol{u}^{\prime}\right)\) para cada uno\(n \geq 1\). Esto se conoce como el teorema de la monotonicidad.
3. Ahora déjese\(\boldsymbol{u}\) y\(\boldsymbol{u}^{\prime}\) sea arbitrario. Vamos\(\alpha=\max _{i}\left(u_{i}-u_{i}^{\prime}\right)\). Demostrar que

   \(\boldsymbol{v}^{*}(n, \boldsymbol{u}) \leq \boldsymbol{v}^{*}\left(n, \boldsymbol{u}^{\prime}\right)+\alpha \boldsymbol{e}.\)

Ejercicio 3.31

Considera un problema de decisión de Markov con M estados en los que algún estado, digamos el estado 1, es inherentemente alcanzable desde el otro estado.

1. Demostrar que debe haber algún otro estado, digamos estado 2, y alguna decisión,\(k_{2}\), tal que\(P_{21}^{\left(k_{2}\right)}>0\).
2. Demostrar que debe haber algún otro estado, digamos estado 3, y alguna decisión,\(k_{3}\), tal que\(P_{31}^{\left(k_{3}\right)}>0\) o bien\(P_{32}^{\left(k_{3}\right)}>0\).
3. Supongamos, para algunos\(i\), y algún conjunto de decisiones\(k_{2}, \ldots, k_{i}\) que, para cada uno\(j\),\(2 \leq j \leq i\),\(P_{j l}^{\left(k_{j}\right)}>0\) para algunos\(l<j\) (es decir, que cada estado de 2 a\(j\) tiene una transición distinta de cero a un estado numerado más bajo). Demostrar que hay algún estado (que no sea 1 a\(i\)), digamos\(i+1\) y alguna decisión\(k_{i+1}\) tal que\(P_{i+1, l}^{\left(k_{i+1}\right)}>0\) para algunos\(l \leq i\) l.
4. Use las partes a), b) y c) para observar que existe una política estacionaria\(\boldsymbol{k}=k_{1}, \ldots, k_{\mathrm{M}}\) para la cual el estado 1 es accesible desde el otro estado.

Ejercicio 3.32

George conduce su auto al teatro, que está al final de una calle de un solo sentido. Hay lugares de estacionamiento a un costado de la calle y una cochera de estacionamiento que cuesta $5 en el teatro. Cada lugar de estacionamiento está ocupado o desocupado de manera independiente con probabilidad 1/2. Si George\(n\) estaciona lugares de estacionamiento lejos del teatro, le cuesta\(n\) centavos (en tiempo y cuero de zapato) caminar el resto del camino. George es miope y sólo puede ver el lugar de estacionamiento por el que actualmente pasa. Si George no se ha estacionado ya para cuando llegue al lugar\(n\) th, primero decide si va a estacionar o no si el lugar está desocupado, y luego observa el lugar y actúa según su decisión. George nunca podrá volver atrás y debe estacionarse en el estacionamiento si no ha estacionado antes.

1. Modele el problema anterior como un problema de programación dinámica de 2 estados. En el estado “conducción”, estado 2, hay dos posibles decisiones: estacionar si el lugar actual está desocupado o conducir sobre si el lugar actual está desocupado o no.
2. Encontrar\(v_{i}^{*}(n, \boldsymbol{u})\), el costo agregado mínimo esperado para\(n\) etapas (es decir, inmediatamente antes de la observación del enésimo lugar de estacionamiento) comenzando en estado\(i = 1\) o 2; es suficiente expresar\(v_{i}^{*}(n, \boldsymbol{u})\) en términos de\(v_{i}^{*}(n-1)\). Los costos finales, en centavos, en la etapa 0 deberían ser\(v_{2}(0)=500, v_{1}(0)=0\).
3. ¿Para qué valores de\(n\) es la decisión óptima la decisión de impulsar?
4. ¿Cuál es la probabilidad de que George se estacione en la cochera, asumiendo que sigue la política óptima?

Ejercicio 3.33 (Comprobante de Corolario 3.6.1)

1. Demostrar que si dos políticas estacionarias\(\boldsymbol{k}^{\prime}\) y\(\boldsymbol{k}\) tienen la misma clase recurrente\(\mathcal{R}^{\prime}\) y si\(k_{i}^{\prime}=k_{i}\) para todos\(i \in \mathcal{R}^{\prime}\), entonces\(w_{i}^{\prime}=w_{i}\) para todos\(i \in \mathcal{R}^{\prime}\). Pista: Ver la primera parte de la prueba de Lemma 3.6.3.
2. Supongamos que\(\boldsymbol{k}^{\prime}\) satisface 3.50 (es decir, que satisface la condición de terminación del algoritmo de mejora de políticas) y que\(\boldsymbol{k}\) satisface las condiciones de la parte a). Demostrar que\ ref {3.64} está satisfecho para todos los estados\(\ell\).
3. \(\boldsymbol{w} \leq \boldsymbol{w}^{\prime}\)Demuéstralo. Pista: Siga el razonamiento al final de la prueba de Lemma 3.6.3.

Ejercicio 3.34

Considere el problema de programación dinámica a continuación con dos estados y dos posibles políticas, denotado\(\boldsymbol{k}\) y\(\boldsymbol{k}^{\prime}\). Las políticas difieren sólo en estado 2.

1. Encuentre la ganancia en estado estacionario por etapa,\(g\) y\(g^{\prime}\), para políticas estacionarias\(\boldsymbol{k}\) y\(\boldsymbol{k}^{\prime}\). \(g=g^{\prime}\)Demuéstralo.
2. Encuentre los vectores de ganancia relativa,\(\boldsymbol{w}\) y\(\boldsymbol{w}^{\prime}\), para políticas estacionarias\(\boldsymbol{k}\) y\(\boldsymbol{k}^{\prime}\).
3. Supongamos que la recompensa final, en la etapa 0, es\(u_{1}=0\),\(u_{2}=u\). ¿Para qué rango de\(u\) utiliza el algoritmo de programación dinámica la decisión\(\boldsymbol{k}\) en el estado 2 en la etapa 1?
4. ¿Para qué rango de\(u\) utiliza el algoritmo de programación dinámica la decisión\(\boldsymbol{k}\) en el estado 2 en la etapa 2? ¿en el escenario\(n\)? Debe encontrar que (para este ejemplo) el algoritmo de programación dinámica utiliza la misma decisión en cada etapa\(n\) que usa en la etapa 1.
5. Encontrar la ganancia óptima\(v_{2}^{*}(n, \boldsymbol{u})\) y\(v_{1}^{*}(n, \boldsymbol{u})\) en función de la etapa\(n\) asumiendo\(u=10\).
6. Encuentra\(\lim _{n \rightarrow \infty} v^{*}(n, \boldsymbol{u})\) y muestra cómo depende de\(u\).

Ejercicio 3.35

Consideremos un problema de decisión de Markov en el que las políticas estacionarias\(\boldsymbol{k}\) y\(\boldsymbol{k}^{\prime}\) cada una satisfacen\ ref {3.50} y cada una corresponden a cadenas ergódicas de Markov.

1. Demostrar que si no\(\boldsymbol{r}^{\boldsymbol{k}^{\prime}}+\left[P^{\boldsymbol{k}^{\prime}}\right] \boldsymbol{w}^{\prime} \geq \boldsymbol{r}^{\boldsymbol{k}}+\left[P^{\boldsymbol{k}}\right] \boldsymbol{w}^{\prime}\) está satisfecho con la igualdad, entonces\(g^{\prime}>g\).
2. Mostrar eso\(\boldsymbol{r}^{\boldsymbol{k}^{\prime}}+\left[P^{\boldsymbol{k}^{\prime}}\right] \boldsymbol{w}^{\prime}=\boldsymbol{r}^{\boldsymbol{k}}+\left[P^{\boldsymbol{k}}\right] \boldsymbol{w}^{\prime}\) (Pista: usar la parte a).
3. Encontrar la relación entre el vector de ganancia relativa\(\boldsymbol{w}^{\boldsymbol{k}}\) para la política\(\boldsymbol{k}\) y el vector relativegain\(\boldsymbol{w}^{\prime}\) para la política\(\boldsymbol{k}^{\prime}\). (Pista: Demuéstralo\(\boldsymbol{r}^{k}+\left[P^{k}\right] \boldsymbol{w}^{\prime}=g \boldsymbol{e}+\boldsymbol{w}^{\prime}\); ¿qué dice esto sobre\(\boldsymbol{w}\) y\(\boldsymbol{w}^{\prime}\)?)
4. Supongamos que la política\(\boldsymbol{k}\) usa la decisión 1 en el estado 1 y la política\(\boldsymbol{k}^{\prime}\) usa la decisión 2 en el estado 1 (es decir,\(k_{1}=1\) para política\(\boldsymbol{k}\) y\(k_{1}=2\) para política\(\boldsymbol{k}^{\prime}\)). ¿Cuál es la relación entre\(r_{1}^{(k)}, P_{11}^{(k)}, P_{12}^{(k)}, \ldots P_{1 J}^{(k)}\) por\(k\) igual a 1 y 2?
5. Ahora supongamos que la política\(\boldsymbol{k}\) usa la decisión 1 en cada estado y la política\(\boldsymbol{k}^{\prime}\) usa la decisión 2 en cada estado. ¿Es posible eso\(r_{i}^{(1)}>r_{i}^{(2)}\) para todos\(i\)? Explique cuidadosamente
6. Ahora supongamos que eso\(r_{i}^{(1)}\) es lo mismo para todos\(i\). ¿Esto cambia tu respuesta a la parte f)? Explique.

Ejercicio 3.36

Considera un problema de decisión de Markov con tres estados. Supongamos que cada política estacionaria corresponde a una cadena ergodica de Markov. Se sabe que una política particular\(\boldsymbol{k}^{\prime}=\left(k_{1}, k_{2}, k_{3}\right)=(2,4,1)\) es la política estacionaria óptima única (es decir, la ganancia por etapa en estado estacionario se maximiza usando siempre la decisión 2 en el estado 1, la decisión 4 en el estado 2 y la decisión 1 en el estado 3). Como de costumbre,\(r_{i}^{(k)}\) denota la recompensa en estado\(i\) bajo decisión\(k\), y\(P_{i j}^{(k)}\) denota la probabilidad de una transición a estado\(j\) dado estado\(i\) y dado el uso de la decisión\(k\) en estado\(i\). Considere el efecto de cambiar el problema de decisión de Markov en cada una de las siguientes formas (los cambios en cada parte deben considerarse en ausencia de los cambios en las otras partes):

1. \(r_{1}^{(1)}\)se sustituye por\(r_{1}^{(1)}-1\).
2. \(r_{1}^{(2)}\)se sustituye por\(r_{1}^{(2)}+1\).
3. \(r_{1}^{(k)}\)se sustituye por\(r_{1}^{(k)}+1\) para todas las decisiones estatales 1\(k\).
4. para todos\(i, r_{i}^{\left(k_{i}\right)}\) se sustituye por\(r^{\left(k_{i}\right)}+1\) para la decisión\(k_{i}\) de política\(\boldsymbol{k}^{\prime}\).

Para cada uno de los cambios anteriores, responda las siguientes preguntas; dé explicaciones:

1. ¿La ganancia por etapa\(g^{\prime}\), aumenta, disminuye o no cambia por el cambio dado?
2. ¿Es posible que otra política,\(k \neq k^{\prime}\), sea óptima después del cambio dado?

Ejercicio 3.37

(El Odoni Bound) Dejar\(\boldsymbol{k}^{\prime}\) ser la política estacionaria óptima para un problema de decisión de Markov y dejar\(g^{\prime}\) y\(\boldsymbol{\pi}^{\prime}\) ser la ganancia correspondiente y la probabilidad de estado estacionario respectivamente. \(v_{i}^{*}(n, \boldsymbol{u})\)Sea la recompensa óptima dinámica esperada por comenzar en estado en\(i\) etapa\(n\) con vector de recompensa final\(\boldsymbol{u}\).

1. Demostrar que\(\min _{i}\left[v_{i}^{*}(n, \boldsymbol{u})-v_{i}^{*}(n-1, \boldsymbol{u})\right] \leq g^{\prime} \leq \max _{i}\left[v_{i}^{*}(n, \boldsymbol{u})-v_{i}^{*}(n-1, \boldsymbol{u})\right]\);\(n \geq 1\). Pista: Considere premultiplicar\(\boldsymbol{v}^{*}(n, \boldsymbol{u})-\boldsymbol{v}^{*}(n-1, \boldsymbol{u})\) por\(\boldsymbol{\pi}^{\prime}\) o\(\boldsymbol{\pi}\) dónde\(\boldsymbol{k}\) está la política dinámica óptima en la etapa\(n\).
2. Mostrar que el límite inferior es no decreciente en\(n\) y el límite superior no aumenta en\(n\) y ambos convergen\(g^{\prime}\) con el aumento\(n\).

Ejercicio 3.38

Considere un sistema de cola de tiempo entero con un búfer finito de tamaño 2. Al inicio del intervalo de\(n^{\text {th }}\) tiempo, la cola contiene como máximo dos clientes. Hay un costo de una unidad por cada cliente en cola (es decir, el costo de retrasar a ese cliente). Si hay un cliente en cola, ese cliente es atendido. Si hay dos clientes, se contrata un servidor extra a un costo de 3 unidades y ambos clientes son atendidos. Por lo tanto, el costo inmediato total para dos clientes en cola es 5, el costo para un cliente es 1, y el costo para 0 clientes es 0. Al final del intervalo\(n\) de tiempo, llegan 0, 1 o 2 nuevos clientes (cada uno con probabilidad 1/3).

1. Supongamos que el sistema comienza con\(0 \leq i \leq 2\) los clientes en cola en el tiempo -1 (es decir, en la etapa 1) y termina en el tiempo 0 (etapa 0) con un costo final\(\boldsymbol{u}\) de 5 unidades por cada cliente en cola (al inicio del intervalo 0). Encuentre el costo agregado esperado\(v_{i}(1, \boldsymbol{u})\) para\(0 \leq i \leq 2\).
2. Supongamos ahora que el sistema inicia con\(i\) los clientes en cola en el tiempo -2 con el mismo costo final en el tiempo 0. Encuentre el costo agregado esperado\(v_{i}(2, \boldsymbol{u})\) para\(0 \leq i \leq 2\).
3. Para una hora de inicio arbitraria\(−n\), encuentre el costo agregado esperado\(v_{i}(n, \boldsymbol{u})\) para\(0 \leq i \leq 2\).
4. Encuentre el costo por etapa y encuentre el vector de costo relativo (ganancia).
5. Ahora supongamos que hay un tomador de decisiones que puede elegir si contratar o no el servidor extra cuando hay dos clientes en cola. Si no se contrata el servidor extra, se guarda la tarifa de 3 unidades, pero solo se atiende a uno de los clientes. Si hay dos llegadas en este caso, supongamos que una es rechazada con un costo de 5 unidades. Encuentre el costo mínimo agregado dinámico esperado\(v_{i}^{*}(1), 0 \leq i \leq\), para la etapa 1 con el mismo costo final que antes.
6. Encuentre el costo mínimo agregado dinámico esperado\(v_{i}^{*}(n, \boldsymbol{u})\) para la etapa\(n\),\(0 \leq i \leq 2\).
7. Ahora asuma un costo final\(\boldsymbol{u}\) de una unidad por cliente en lugar de 5, y encuentre el nuevo costo agregado dinámico mínimo esperado\(v_{i}^{*}(n, \boldsymbol{u}), 0 \leq i \leq 2\).