10.7: Procesamiento de Tiempo Discreto de Señales de Tiempo Continuas
- Page ID
- 86463
Introducción
Las computadoras digitales pueden procesar señales de tiempo discretas utilizando algoritmos extremadamente flexibles y potentes. Sin embargo, la mayoría de las señales de interés son señales de tiempo continuas, que es como los datos casi siempre aparecen en la naturaleza. Ahora que se ha discutido la teoría que soporta métodos para generar una señal de tiempo discreta a partir de una señal de tiempo continua a través del muestreo y luego reconstruir perfectamente la señal original a partir de sus muestras sin error, se mostrará cómo esto se puede aplicar para implementar tiempo continuo, tiempo lineal sistemas invariantes que utilizan sistemas invariantes de tiempo discreto, tiempo lineal. Esto es de importancia clave para muchas tecnologías modernas ya que permite aprovechar el poder de la computación digital para el procesamiento de señales analógicas.
Procesamiento de tiempo discreto de señales de tiempo continuas
Estructura de Proceso
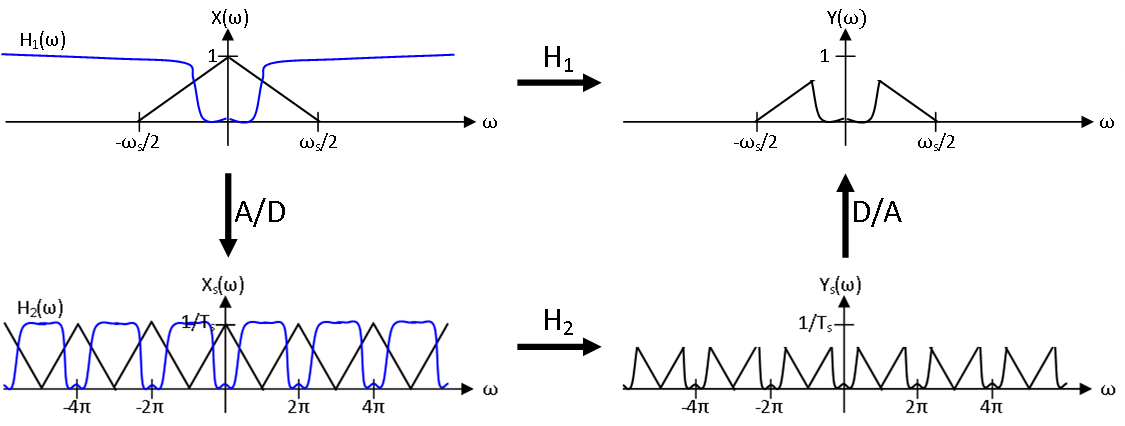
Con el objetivo de procesar señales de tiempo continuas utilizando un sistema de tiempo discreto, ahora examinaremos una de las estructuras más comunes de las tecnologías de procesamiento de señales digitales. Como una visión general del enfoque adoptado, la señal de tiempo continua original\(x\) se muestrea a una señal\(x_s\) de tiempo discreta de tal manera que los períodos del espectro\(X_s\) de muestras están lo más cerca posible en forma al espectro de\(X\). Luego\(H_2\) se aplica un filtro de tiempo discreto, tiempo lineal invariante, que modifica la forma del espectro de muestras\(X_s\) pero no puede aumentar el límite de banda de\(X_s\), para producir otra señal\(y_s\). Esto se reconstruye con un filtro de reconstrucción adecuado para producir una señal de salida de tiempo continuo\(y\), implementando así efectivamente algún sistema de tiempo continuo\(H_1\). Este proceso se ilustra en la Figura\(\PageIndex{1}\), y los espectros se muestran para un caso específico en la Figura\(\PageIndex{2}\).
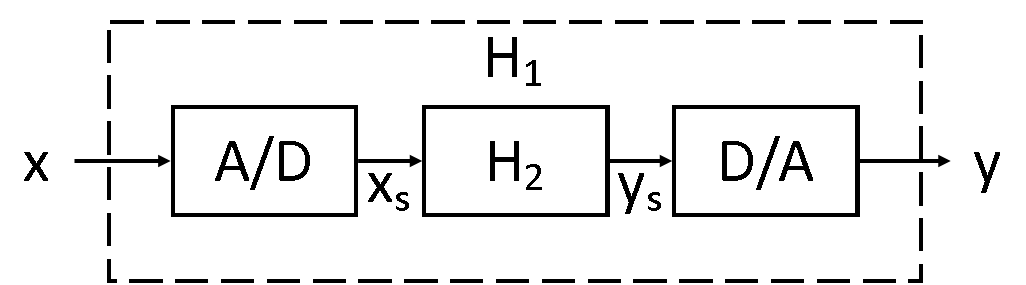
Es necesaria una mayor discusión sobre cada uno de estos pasos, y comenzaremos discutiendo el convertidor analógico a digital, a menudo denotado por ADC o A/D, Es claro que para procesar una señal de tiempo continua utilizando técnicas de tiempo discretas, debemos muestrear la señal como paso inicial. Este es esencialmente el propósito del ADC, aunque hay temas prácticos que se discutirán más adelante. Un ADC toma una señal analógica de tiempo continuo como entrada y produce una señal digital de tiempo discreta como salida, con el caso de precisión infinita ideal correspondiente al muestreo. Como afirma el teorema de Nyquist-Shannon Sampling, con el fin de retener toda la información sobre la señal original, generalmente deseamos una muestra por encima de la frecuencia de Nyquist\(\omega_s≥2B\) donde la señal original está limitada a la banda\((−B,B)\). Cuando no sea posible garantizar esta condición, se debe utilizar un filtro anti-aliasing.
El filtro de tiempo discreto es donde ocurren las modificaciones intencionales a la información de la señal. Esto se hace comúnmente en software de computadora digital después de que la señal haya sido muestreada por un ADC de hardware y antes de que sea utilizada por un DAC de hardware para construir la salida. Esto permite que la configuración anterior sea bastante flexible en el filtro que implementa. Si muestreos por encima de la frecuencia Nyquist el. Cualquier modificación que haga el filtro discreto a esta forma se puede pasar a una señal de tiempo continua asumiendo una reconstrucción perfecta. En consecuencia, el proceso descrito implementará un filtro de tiempo continuo, tiempo lineal invariante. Esto se explicará con más detalle matemático en la siguiente sección. Como es habitual, hay, desde luego, limitaciones prácticas que se discutirán más adelante.
Finalmente, discutiremos el convertidor digital a analógico, a menudo denotado por DAC o D/A Dado que los filtros de tiempo continuo tienen entradas de tiempo continuas y salidas de tiempo continuas, debemos construir una señal de tiempo continua a partir de nuestra señal de tiempo discreta filtrada. Suponiendo que hemos muestreado una banda limitada a una tasa suficientemente alta, en el caso ideal esto se haría usando una reconstrucción perfecta a través de la fórmula de interpolación Whittaker-Shannon. No obstante, hay, una vez más, temas prácticos que impiden que esto suceda y que se discutirán más adelante.
Filtro de Tiempo Discreto
Con alguna discusión inicial del proceso ilustrado en la Figura\(\PageIndex{1}\) completa, se\(H_2\) puede explorar la relación entre el filtro de tiempo continuo, tiempo lineal invariante\(H_1\) y el tiempo discreto, filtro lineal invariante. Asumiremos el uso de ADC y DAC ideales e infinitos de precisión que realizan muestreo y reconstrucción perfecta, respectivamente, utilizando una frecuencia de muestreo\(\omega_s=2 \pi /T_s≥2B\) donde la señal de entrada\(x\) está limitada en banda\((−B,B)\). Tenga en cuenta que estos argumentos fallan si no se cumple esta condición y se produce el aliasing. En ese caso, es necesaria la aplicación previa de un filtro anti-aliasing para que estos argumentos se mantengan.
Recordemos que ya hemos calculado el espectro\(X_s\) de las muestras\(x_s\) dado una entrada\(x\) con espectro\(X\) como
\[X_{s}(\omega)=\frac{1}{T_{s}} \sum_{k=-\infty}^{\infty} X\left(\frac{\omega-2 \pi k}{T_{s}}\right) . \nonumber \]
Asimismo, el espectro\(Y_s\) de las muestras\(y_s\) dadas una salida\(y\) con espectro\(Y\) es
\[Y_{s}(\omega)=\frac{1}{T_{s}} \sum_{k=-\infty}^{\infty} Y\left(\frac{\omega-2 \pi k}{T_{s}}\right) . \nonumber \]
Del conocimiento de que\(y_s=(H_1x)_s=H_2(x_s)\), se deduce que
\[\sum_{k=-\infty}^{\infty} H_{1}\left(\frac{\omega-2 \pi k}{T_{s}}\right) X\left(\frac{\omega-2 \pi k}{T_{s}}\right)=H_{2}(\omega) \sum_{k=-\infty}^{\infty} X\left(\frac{\omega-2 \pi k}{T_{s}}\right). \nonumber \]
Debido a\(X\) que es banda limitada a\((−\pi /T_s, \pi /T_s)\), podemos concluir que
\[H_{2}(\omega)=\sum_{k=-\infty}^{\infty} H_{1}\left(\frac{\omega-2 \pi k}{T_{s}}\right)(u(\omega-(2 k-1) \pi)-u(\omega-(2 k+1) \pi)). \nonumber \]
Más simplemente dicho,\(H_2\) es\(2 \pi\) periódico y\(H_2(\omega)=H_1( \omega /T_s)\) para\(\omega \in[-\pi, \pi)\).
Dado un filtro específico de tiempo continuo, tiempo lineal invariante\(H_1\), la ecuación anterior resuelve el problema de diseño del sistema siempre que sepamos cómo implementar\(H_2\). El filtro\(H_2\) debe elegirse de tal manera que tenga una respuesta de frecuencia donde cada periodo tenga la misma forma que la respuesta de frecuencia de\(H_1\) on\(\left(-\pi / T_{s}, \pi / T_{s}\right)\). Esto se ilustra en las respuestas de frecuencia mostradas en la Figura\(\PageIndex{2}\).
También podríamos considerar el problema de análisis del sistema en el que\(H_2\) se da un filtro específico de tiempo discreto, tiempo lineal invariante, y queremos describir el filtro\(H_1\). Hay muchos filtros de este tipo, pero podemos describir sus respuestas de frecuencia\(\left(-\pi / T_{s}, \pi / T_{s}\right)\) usando la ecuación anterior. Aislar un periodo de\(H_2(\omega)\) arroja la conclusión de que\(H_{1}(\omega)=H_{2}\left(\omega T_{s}\right)\) para\(\omega \in\left(-\pi / T_{s}, \pi / T_{s}\right)\). Debido a que\(x\) se asumió que estaba limitado a banda\(\left(-\pi / T_{s}, \pi / T_{s}\right)\), el valor de la respuesta de frecuencia en otros lugares es irrelevante.
Consideraciones prácticas
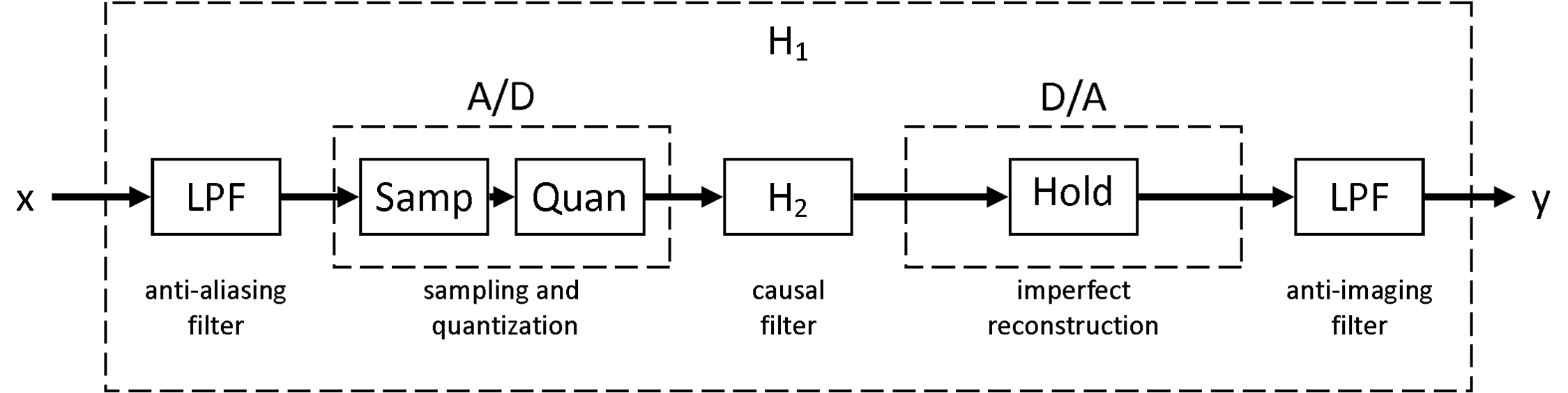
Como se mencionó anteriormente, existen varias consideraciones prácticas que deben abordarse en cada etapa del proceso mostrado en la Figura\(\PageIndex{1}\). Algunos de estos se abordarán brevemente aquí, y en la Figura aparece un modelo más completo de cómo el procesamiento de tiempo discreto de las señales de tiempo continuas\(\PageIndex{3}\).
Filtro Anti-Aliasing
En realidad, normalmente no podemos garantizar que la señal de entrada tenga un límite de banda específico, y no necesariamente se pueden producir velocidades de muestreo suficientemente altas. Dado que es imperativo que no se permita que los componentes de frecuencia más alta se enmascaren como componentes de menor frecuencia a través del aliasing, se\(\omega_s/2\) deben usar filtros antialiasing con frecuencia de corte menor o igual a antes de que la señal se alimente al ADC. El diagrama de bloques de la Figura\(\PageIndex{3}\) refleja esta adición.
Como se describe en la sección anterior,\(\omega_s/2\) sería óptimo un filtro de paso bajo ideal que elimine toda la energía a las frecuencias anteriores. Por supuesto, esto no es alcanzable, por lo que se\(\omega_s/2\) deben aceptar aproximaciones del filtro de paso bajo ideal con baja ganancia superior. Esto significa que algún aliasing es inevitable, pero se puede reducir a un nivel mayormente insignificante.
Cuantización de señal
En nuestra discusión anterior sobre el procesamiento de tiempo discreto de señales de tiempo continuas, habíamos asumido un caso ideal en el que el ADC realiza muestreo exactamente. Sin embargo, mientras que un ADC convierte una señal de tiempo continua en una señal de tiempo discreta, también debe convertir valores analógicos en valores digitales para su uso en un dispositivo lógico digital, un fenómeno llamado cuantificación. El subsistema ADC del diagrama de bloques de la Figura\(\PageIndex{3}\) refleja esta adición.
Los datos obtenidos por el ADC deben almacenarse en muchos bits finitamente dentro de un dispositivo lógico digital. De esta manera, solo hay finitamente muchos valores que una muestra digital puede tomar, específicamente\(2N\) dónde\(N\) está el número de bits, mientras que hay incontables muchos valores que una muestra analógica puede tomar. De ahí que algo se debe perder en el proceso de cuantificación. El resultado es que la cuantificación limita tanto el rango como la precisión de la salida del ADC. Ambos son finitos, y mejorar uno a un número constante de bits requiere sacrificar la calidad en el otro.
Implementabilidad del filtro
En circunstancias del mundo real, si la señal de entrada es una función del tiempo, los valores futuros de la señal no se pueden utilizar para calcular la salida. Así, el filtro digital\(H_2\) y el sistema general\(H_1\) deben ser causales. La anotación de filtro en la Figura\(\PageIndex{3}\) refleja esta adición. Si el sistema deseado no es causal sino que tiene respuesta de impulso igual a cero antes de algún tiempo\(t_0\), se puede introducir un retraso para hacerlo causal. Sin embargo, si este retraso es excesivo o la respuesta al impulso tiene una longitud infinita, se hace necesario un esquema de ventanas para resolver prácticamente el problema. Multiplicar por una ventana para disminuir la duración de la respuesta de impulso puede reducir el retraso necesario y disminuir los requisitos computacionales.
Tomemos, por ejemplo, el caso del filtro de paso bajo ideal. Es acausal e infinito en longitud en ambas direcciones. Así, debemos satisfacernos con una aproximación. Se podría sugerir que estas aproximaciones podrían lograrse truncando la respuesta al impulso sinc del filtro de paso bajo en uno de sus ceros, efectivamente enventanándolo con un pulso rectangular. Sin embargo, hacerlo produciría malos resultados en el dominio de la frecuencia ya que la convolución resultante extendería significativamente la energía de la señal. Otras funciones de ventanas, de las cuales hay muchas, propagan la señal menos en el dominio de la frecuencia y, por lo tanto, son mucho más útiles para producir estas aproximaciones.
Filtro Anti-Imagenología
En nuestra discusión anterior sobre el procesamiento de tiempo discreto de señales de tiempo continuas, habíamos asumido un caso ideal en el que el DAC realiza una reconstrucción perfecta. Sin embargo, al considerar cuestiones prácticas, es importante recordar que la función sinc, que se utiliza para la interpolación Whittaker-Shannon, es infinita en longitud y acausal. De ahí que sería imposible que un DAC implemente una reconstrucción perfecta.
En cambio, el DAC implementa una retención causal de orden cero u otro esquema de reconstrucción simple con respecto a la tasa de muestreo\(\omega_s\) utilizada por el ADC. Sin embargo, al hacerlo se traducirá en una función que no está limitada en banda\((−\omega_s/2,\omega_s/2)\). Por lo tanto, se debe aplicar a la salida un filtro de paso bajo adicional, llamado filtro anti-imagen. El proceso ilustrado en la Figura\(\PageIndex{3}\) refleja estas adiciones. El filtro anti-imagen intenta limitar la banda de la señal a\((−\omega_s/2,\omega_s/2)\), por lo que un filtro de paso bajo ideal sería óptimo. No obstante, como ya se ha dicho, esto no es posible. Por lo tanto,\(\omega_s/2\) deben aceptarse aproximaciones del filtro de paso bajo ideal con baja ganancia superior. El filtro anti-imagen normalmente tiene las mismas características que el filtro anti-aliasing.
Resumen de procesamiento de tiempo discreto de señales de tiempo continuas
Como se ha demostrado, el muestreo y la reconstrucción se pueden utilizar para implementar sistemas de tiempo continuo utilizando sistemas de tiempo discretos, lo cual es muy potente debido a la versatilidad, flexibilidad y velocidad de las computadoras digitales. Sin embargo, hay una gran cantidad de consideraciones prácticas que deben tenerse en cuenta al intentar lograr esto, incluyendo ruido de cuantificación y antialiasing en el convertidor analógico a digital, implementabilidad del filtro en el filtro de tiempo discreto y ventanas de reconstrucción y asociados problemas en el convertidor digital a analógico. Muchas tecnologías modernas abordan estos temas y hacen uso de este proceso.


