9.5: Problemas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Sección 9.1
Deseamos encontrar las propiedades de las ondas que se propagan dentro de un medio dieléctrico lineal que también tenga una conductividad óhmicaσ.
(a) ¿Cuáles son las ecuaciones de Maxwell en este medio?
(b) Definir potenciales vectoriales y escalares, ¿qué condición de calibre desacopla estos potenciales?
(c) Una carga puntual ar=0 varía sinusoidalmente con el tiempo comoQ(t)=Re(ˆQejωt). ¿Cuál es el potencial escalar?
d) Repetir los apartados a) a c) para las ondas en un medio plasmático con derecho constitutivo
∂Jf∂t=ω2pεE
Una hoja de corriente infinita enz=0 varía comoRe[K0ej(ωt−kxx)ix]
(a) Encontrar los potenciales vectoriales y escalares.
b) ¿Cuáles son los campos eléctrico y magnético?
(c) Repita (a) y (b) si la corriente se distribuye uniformemente sobre una losa plana de espesor2a:
\ (\ textbf {J} _ _ {f} =\ izquierda\ {\ begin {array} {ll}
\ displaystyle J_ {0} e^ {j\ left (\ omega t-k_ {x} x\ derecha)}\ textbf {i} _ _ {x}, &\ quad -a< z< a\
\\ displaystyle 0, & quad\ izquierda |z\ derecha |> a
\ end {array}\ derecho.\)
Una esfera de radioR tiene una distribución uniforme de carga superficialσf=Re(ˆσ0ejωt) donde la carga superficial variable en el tiempo se debe a una corriente de conducción puramente radial.
(a) Encontrar los potenciales escalares y vectoriales, dentro y fuera de la esfera. (Pista:r2QP=r2+R2−2rRcosθ;rQPdrQP=rRsinθdθ.)
b) ¿Cuáles son los campos eléctricos y magnéticos en todas partes?
Sección 9.2
Encuentre las longitudes efectivas, las resistencias a la radiación y las distribuciones de carga de línea para cada una de las siguientes distribuciones de corriente válidas para en un dipolo eléctrico puntual con longitud corta|z|<dl/2:
(a)ˆI(z)=I0cosαz
b)ˆI(z)=I0e−α|z|
c)ˆI(z)=I0coshαz
¿Cuál es la densidad de potencia promedio en el tiempo, la potencia promedio en el tiempo total y la resistencia a la radiación de un dipolo magnético puntual?
Un campoRe(E0ejωt) eléctrico de onda plana incide sobre una partícula esférica perfectamente conductora de radioR que es mucho más pequeña que la longitud de onda.
a) ¿Cuál es el momento dipolo inducido? (Pista: Ver Sección 4-4-3.)
(b) Si la partícula pequeña es, en cambio, un dieléctrico puro sin pérdidas con permitividadε, ¿cuál es el momento dipolar inducido?
c) Para ambos casos, ¿cuál es la potencia dispersa promedio en el tiempo?
Un campoRe(H0ejωt) magnético de onda plana incide sobre una partícula perfectamente conductora que es mucho más pequeña que la longitud de onda.
(a) ¿Cuál es el momento dipolo magnético inducido? (Pista: Ver Sección 5-7-2ii y 5-5-1.)
b) ¿Cuáles son los campos eléctricos y magnéticos re-radiados?
c) ¿Cuál es la potencia dispersa promedio en el tiempo? ¿Cómo varía con la frecuencia?
(a) Para el dipolo magnético, ¿cómo se relacionan las líneas del campo magnético con el potencial vectorialA?
b) ¿Cuál es la ecuación de estas líneas de campo?
Sección 9.3
Dos dipolos alineadosˆI1dl yˆI2dl se colocan a lo largo delz eje a una distancia de2a distancia. Los dipolos tienen la misma longitud mientras que las corrientes tienen magnitudes iguales pero diferencia de faseX.
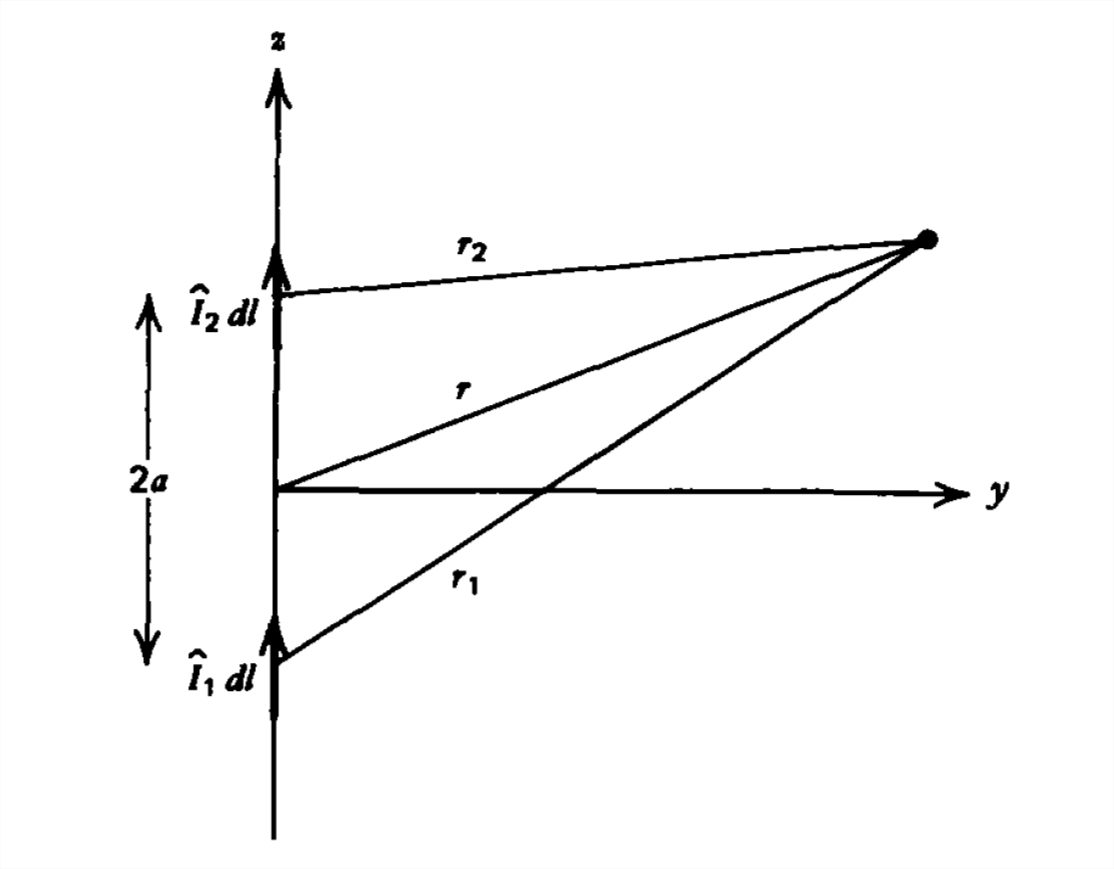
a) ¿Cuáles son los campos eléctricos y magnéticos lejanos?
b) ¿Cuál es la densidad de potencia promedio en el tiempo?
c) ¿En qué ángulos es cero o máxima la densidad de potencia?
(d) Porque2a=λ/2, ¿qué valores deX dar una matriz broadside o end-fire?
(e) Repita (a) - (c) para dipolos alineados2N+1 igualmente espaciados a lo largo delz eje con diferencia de fase incrementalX0.
Tres dipolos de igual longituddl se colocan a lo largo delz eje.
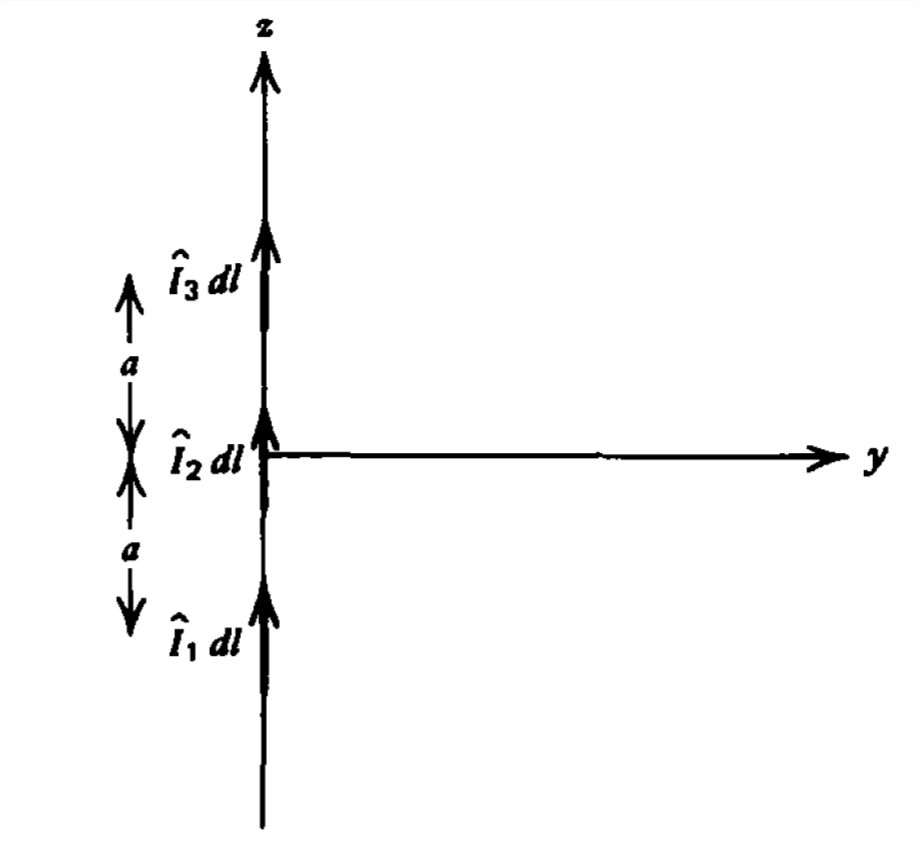
(a) Encontrar los campos eléctricos y magnéticos lejanos.
b) ¿Cuál es la densidad de potencia promedio en el tiempo?
(c) Para cada uno de los siguientes casos encontrar los ángulos donde la densidad de potencia sea cero o máxima.
(i)ˆI1=ˆI3=ˆI0,ˆI2=2ˆI0
ii)ˆI1=ˆI3=ˆI0,ˆI2=−2ˆI0
iii)ˆI1=−ˆI3=ˆI0,ˆI2=2jˆI0
Muchos dipolos puntuales estrechamente espaciados de longituddl colocados a lo largo delx eje accionado en fase se aproximan a una hojaRe(K0ejωtiz) de longitud de corrientez dirigida por zL.
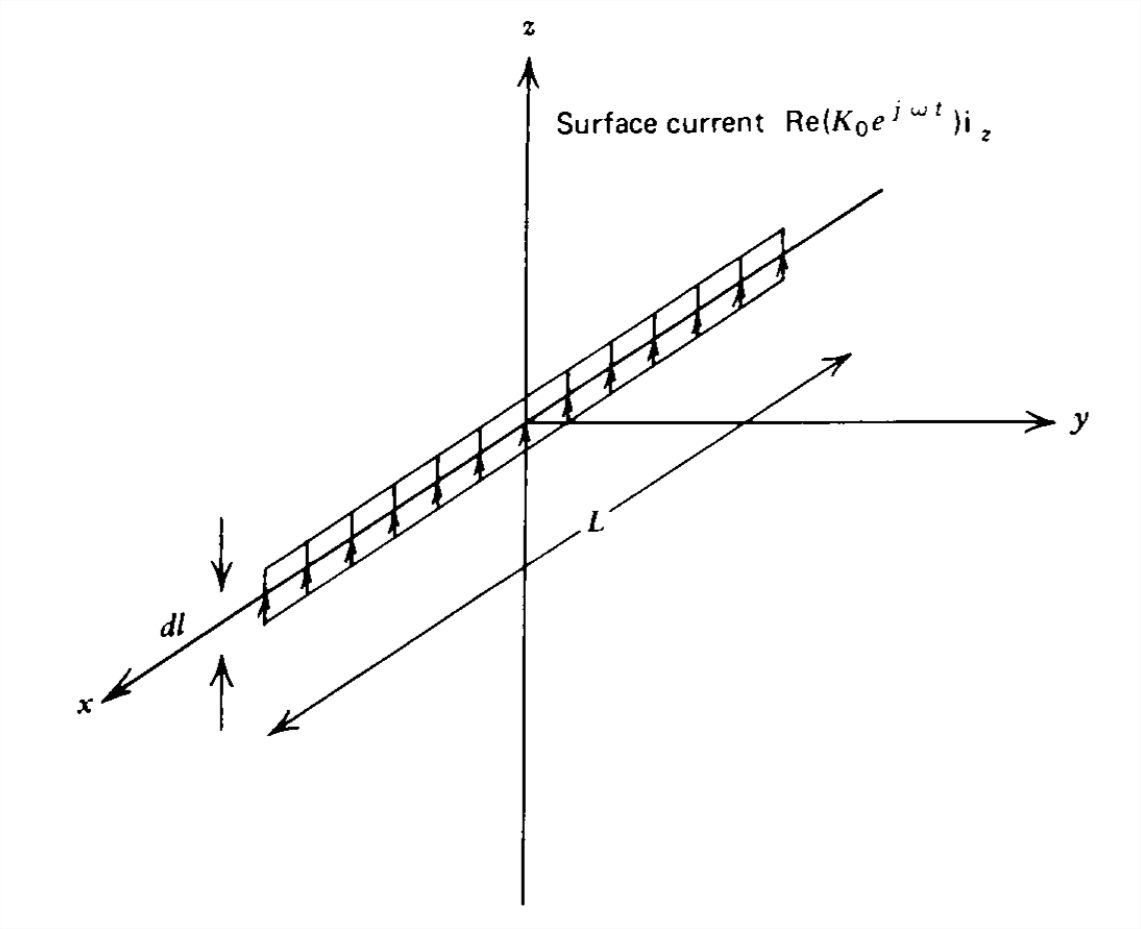
(a) Encuentra los campos lejanos de esta hoja actual.
b) ¿En qué ángulos es mínima o máxima la densidad de potencia?
Sección 9.4
Encuentre los campos lejanos y la densidad de potencia promedio en el tiempo para cada una de las siguientes distribuciones de corriente en un dipolo largo:
\ (\ left (a\ right)\ quad\ hat {I}\ left (z\ right) =\ left\ {\ begin {array} {ll}
I_ {0}\ left (1-2z/L\ right), &\ quad 0< z< z< L/2\
I_ {0}\ left (1+2z/L\ right), &\ quad -L/2 < z< 0
\ end {array}\ derecho.\)
Pista:
∫zeazdz=eaza2(az−1)
(b)ˆI(z)=I0cosπz/L,−L/2<z<L/2
Pista:
∫eazcospzdz=eaz(acospz+psinpz)(a2+p2)
(c)Para estos casos encontrar la resistencia a la radiación cuandokL≪1.


