2.2: La Gráfica de una Función

René Descartes (1596-1650) fue un filósofo y matemático francés que es bien conocido por la famosa frase “cogito ergo sum” (creo, por lo tanto soy), que aparece en su Discursos de la methode pour bien conduire sa raison, et chercher la verite dans les sciences (Discurso sobre el método de la razón Dirigir la razón y buscar la verdad en las ciencias). En ese mismo tratado, Descartes introduce su sistema de coordenadas, un método para representar puntos en el plano a través de pares de números reales. En efecto, el plano cartesiano de la actualidad se llama así en honor a René Descartes, a quien algunos llaman el “Padre de las Matemáticas Modernas”.

El trabajo de Descartes, que vinculó para siempre la geometría y el álgebra, continuó en un apéndice del Discurso sobre el método, titulado La Geometrie, que algunos consideran el comienzo de las matemáticas modernas. Ciertamente, tanto Newton como Leibniz, en el desarrollo del Cálculo, construyeron sobre los cimientos proporcionados en esta obra por Descartes.

Un Sistema de Coordenadas Cartesianas consiste en un par de ejes, generalmente dibujados en ángulo recto entre sí en el plano, uno horizontal (etiquetado x) y otro vertical (etiquetado y), como se muestra en la Figura\(\PageIndex{1}\). Los cuadrantes se numeran I, II, III y IV, en orden antihorario, y se muestran muestras de pares ordenados de la forma (x, y) en cada cuadrante del sistema de coordenadas cartesianas en la Figura\(\PageIndex{1}\).

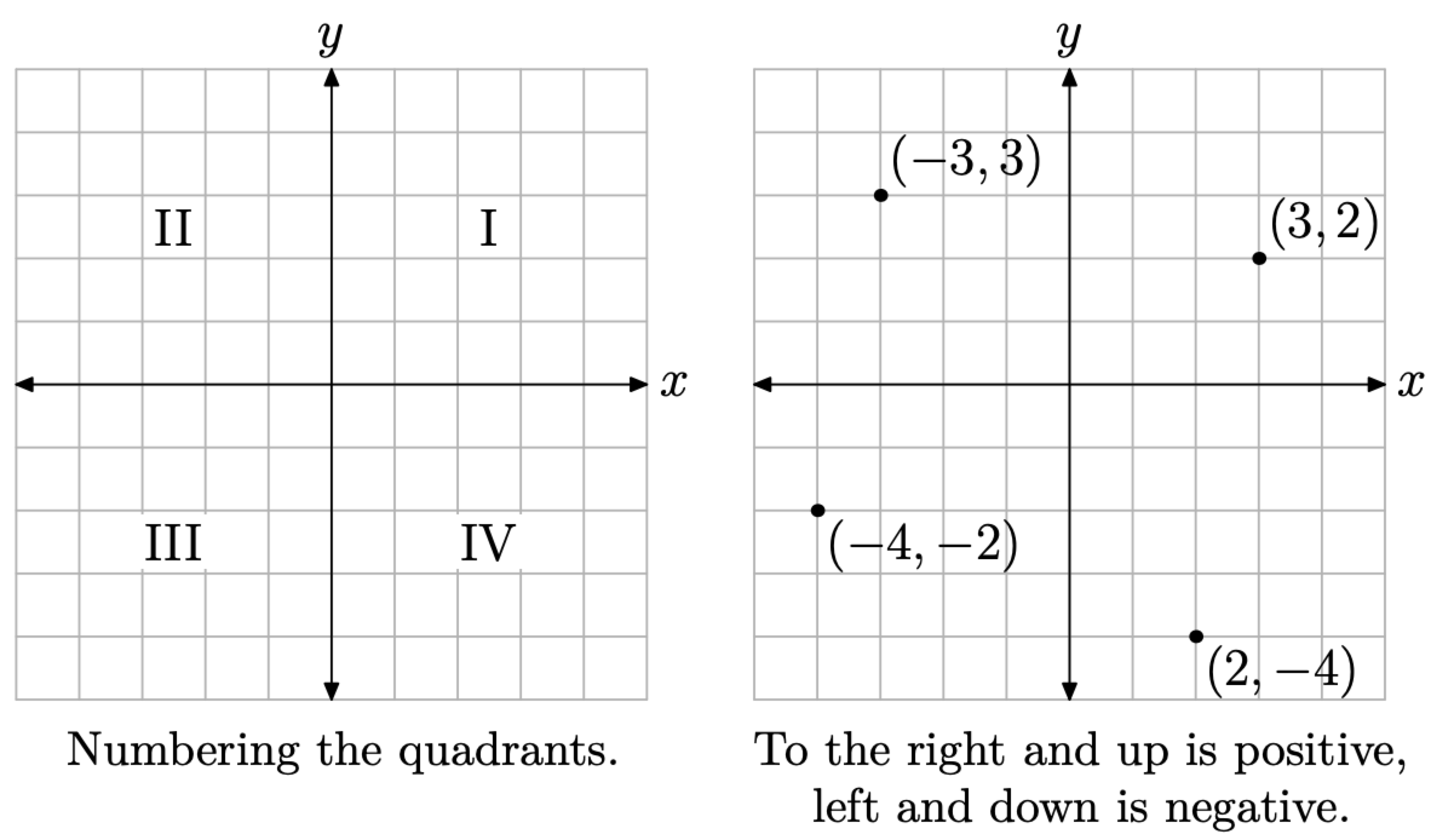
Figura\(\PageIndex{1}\). El sistema de coordenadas cartesianas.

Ahora, supongamos que tenemos una relación\[R=\{(1,2),(3,1),(3,4),(4,3)\}\]

Recordemos que relación es el nombre que se le da a una colección de pares ordenados. En la Figura\(\PageIndex{2}\) (b) hemos trazado cada uno de los pares ordenados en la relación R. Esto se llama el gráfico de la relación R.

Definición

La gráfica de una relación es la colección de todos los pares ordenados de la relación. Estos generalmente se representan como puntos en un sistema de coordenadas cartesianas.

Figura\(\PageIndex{2}\) Un diagrama de mapeo y su gráfica.

En la Figura\(\PageIndex{2}\) (a), hemos creado un diagrama de mapeo de los pares ordenados. Tenga en cuenta que el objeto de dominio 3 está emparejado con dos elementos de rango, a saber, 1 y 4. De ahí que la relación R no sea una función. Es interesante señalar que hay dos puntos en la gráfica de R en la Figura\(\PageIndex{2}\) (b) que tienen la misma primera coordenada, a saber (3, 1) y (3, 4). Esta es una señal de que la gráfica de la relación R no es una función. En la siguiente sección discutiremos la Prueba de Línea Vertical, que utilizará este doble uso de la primera coordenada para determinar cuándo una relación no es una función.

Creación de la Gráfica de una Función

Algunos textos hablarán de la gráfica de una ecuación, como “Dibuja la gráfica de la ecuación”\(y=x^{2}\). Esta instrucción plantea una serie de dificultades.

• Primero, la instrucción no da dirección al lector; es decir, ¿qué significa la instrucción? No es muy útil.
• En segundo lugar, la instrucción es incorrecta. No se dibujan las gráficas de ecuaciones. Más bien, dibujas las gráficas de relaciones y/o funciones. Una gráfica es solo otra forma de representar una función, una relación que empareja cada elemento en su dominio con exactamente un elemento en su rango.

Entonces, ¿cuál es la instrucción adecuada? Primero, proporcionaremos la definición formal de la gráfica de una función, luego la desglosaremos por medio de ejemplos.

Definición

La gráfica de una función es la colección de todos los pares ordenados de la función. Estos generalmente se representan como puntos en un sistema de coordenadas cartesianas.

Como ejemplo, considere la función

\[f=\{(1,2),(2,4),(3,1),(4,3)\}\]

Los lectores notarán que cada objeto en el dominio está emparejado con uno y solo un objeto en el rango, como se ve en el diagrama de mapeo de la Figura\(\PageIndex{3}\) (a).

Así, tenemos dos representaciones de la función f, la colección de pares ordenados (3), y el diagrama de mapeo de la Figura\(\PageIndex{3}\) (a). Una tercera representación de la función f es la gráfica de los pares ordenados de la función, mostrada en el plano cartesiano en la Figura\(\PageIndex{3}\) (b).

Figura\(\PageIndex{3}\) Un diagrama de mapeo y su gráfica.

Cuando la función está representada por una ecuación o fórmula, entonces ajustamos algo nuestra definición de su gráfica.

Definición

La gráfica de f es el conjunto de todos los pares ordenados de\((x, f(x))\) manera que x esté en el dominio de f. En símbolos,

\[\text {Graph of } f=\{(x, f(x)) : x \text { is in the domain of } f .\}\]

Esta última definición se explica más fácilmente con el ejemplo. Entonces, definamos una función f que mapee cualquier número real x al número real\(x^{2}\); es decir, let\(f(x)=x^{2}\). Ahora bien, según Definición, la gráfica de f es el conjunto de todos los puntos\((x, f(x))\), de tal manera que x está en el dominio de f.

El camino ahora está claro. Comenzamos creando una tabla de puntos\((x, f(x))\), donde x está en el dominio de la función f definida por\(f(x) = x^{2}\). La elección de x es tanto subjetiva como experimental, por lo que comenzamos eligiendo valores enteros de x entre −3 y 3. Luego evaluamos la función en cada uno de estos valores x (e.g.,\(f(-3)=(-3)^{2}=9\)). Los resultados se muestran en la tabla de la Figura\(\PageIndex{4}\) (a). Luego trazamos los puntos de nuestra tabla en el plano cartesiano como se muestra en la Figura\(\PageIndex{4}\) (b).

Figura\(\PageIndex{4}\). Trazar pares que satisfagan la relación funcional definida por la ecuación\(f(x)=x^{2}\).

Si bien este es un buen comienzo, la gráfica de la Figura\(\PageIndex{4}\) (b) está lejos de ser completa. La definición requiere que trazemos los pares ordenados\((x, f(x))\) para cada valor de x que esté en el dominio de f. Solo hemos trazado siete de esos puntos, así que no hemos terminado. Vamos a agregar más puntos a la gráfica de f. Evaluaremos la función en cada uno de los valores x mostrados en la tabla de la Figura\(\PageIndex{5}\) (a), luego graficaremos los pares adicionales\((x, f(x))\) de la tabla en el plano cartesiano, como se muestra en la Figura\(\PageIndex{5}\) (b).

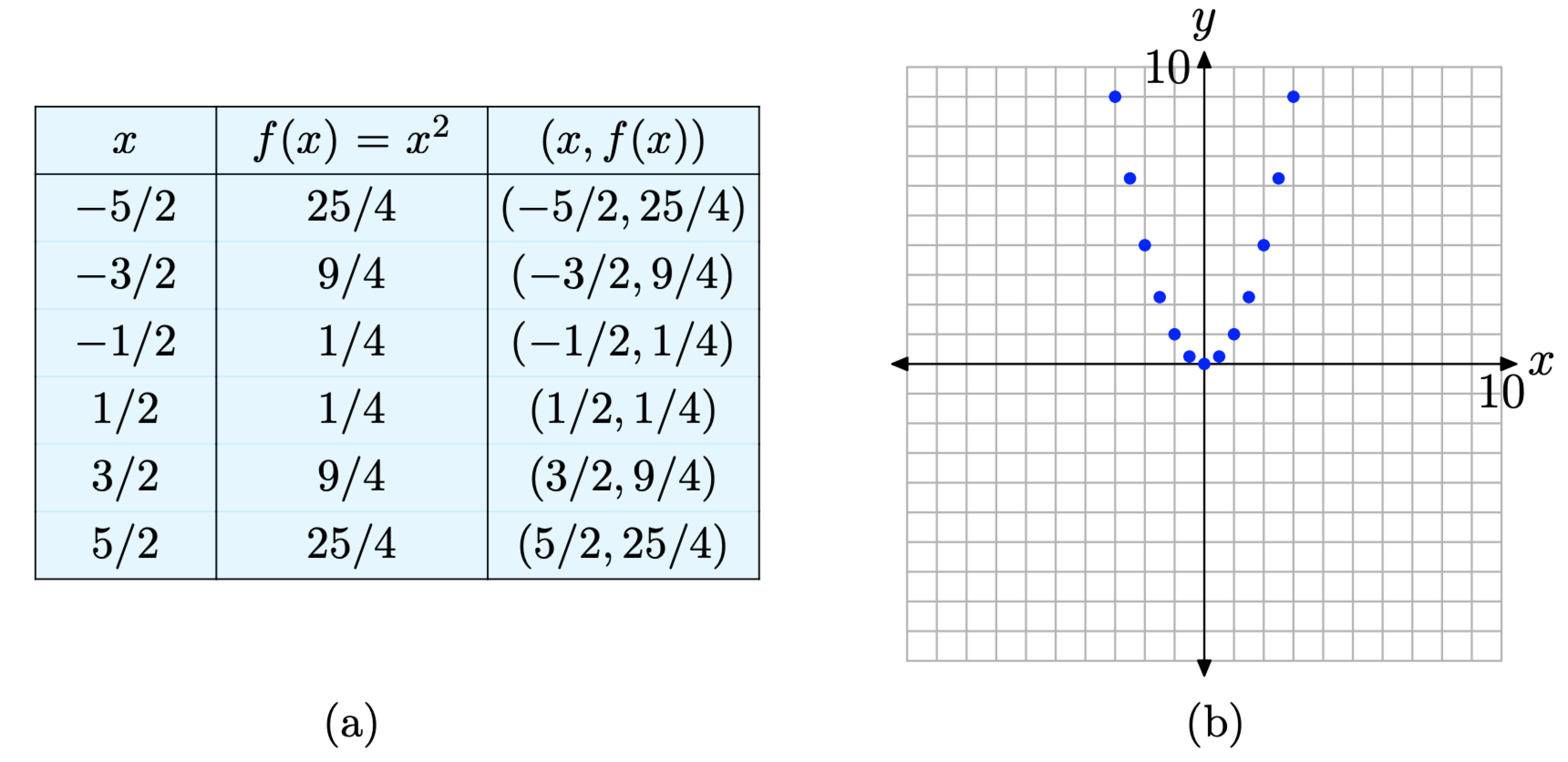
Figura\(\PageIndex{5}\). Trazar pares adicionales\((x, f(x))\) definidos por la ecuación\(f(x) = x^{2}\).

Todavía no hemos terminado, porque sólo hemos trazado 13 pares\((x, f(x))\), tal que\(f(x) = x^{2}\). La definición 4 requiere que trazemos los pares ordenados\((x, f(x))\) para cada valor de x en el dominio de f.

Sin embargo, un patrón ciertamente se está estableciendo, como se ve en la Figura\(\PageIndex{5}\) (b). En algún momento, necesitamos “dar un salto de fe”, y trazar todos los pares ordenados\((x, f(x))\), de tal manera que x esté en el dominio de f. Esto se hace en la Figura\(\PageIndex{6}\).

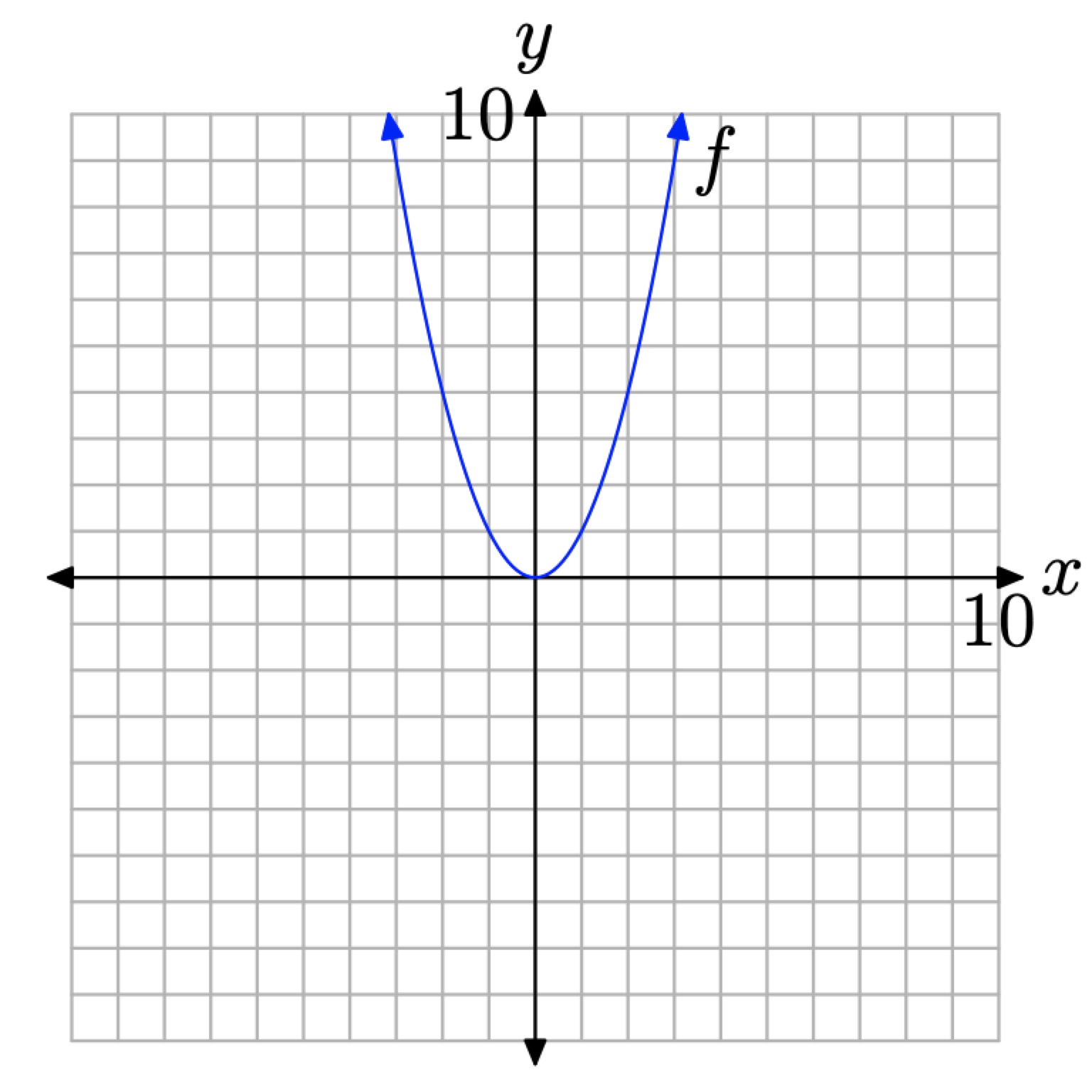
Figura\(\PageIndex{6}\). Trazando todos los pares\((x, f(x))\) para que x esté en el dominio de f.

Hay varios puntos importantes que debemos hacer sobre el resultado final en la Figura\(\PageIndex{6}\).

• Cuando dibujamos una curva suave, como la que se muestra en la Figura\(\PageIndex{6}\), es importante entender que esto es simplemente un atajo para trazar todos los pares (x, f (x)), donde\(f(x) = x^{2}\) y x está en el dominio de f.
• Es importante entender que NO estamos “conectando los puntos”, ni con una regla ni con segmentos curvos. Más bien, la curva en la Figura\(\PageIndex{6}\) es el resultado de trazar todos los pares individuales\((x, f(x))\).
• Las “flechas” en cada extremo de la curva tienen un significado importante. Por mucho que los puntos suspensivos al final de la progresión\(2,4,6, \dots\) significan “etcétera”, las flechas en cada extremo de la curva tienen un significado similar. La flecha al final de la mitad izquierda de la curva indica que la gráfica continúa abriéndose hacia arriba y hacia la izquierda, mientras que la flecha al final de la mitad derecha de la curva indica que la gráfica continúa abriéndose hacia arriba y hacia la derecha.

Creando Gráficas a Mano

Vamos a ver varias gráficas básicas, las cuales crearemos empleando la estrategia utilizada para crear la gráfica de\(f(x) = x^{2}\). Primero, vamos a resumir ese proceso.

Resumen

Si una función está definida por una ecuación, puede crear la gráfica de la función de la siguiente manera.

1. Seleccione varios valores de x en el dominio de la función f.
2. Utilice los valores seleccionados de x para crear una tabla de pares (x, f (x)) que satisfagan la ecuación que define la función f.
3. Crear un sistema de coordenadas cartesianas en una hoja de papel cuadriculado. Etiquete y escale cada eje, luego grafique los pares (x, f (x)) de su tabla en su sistema de coordenadas.
4. Si los pares trazados (x, f (x)) proporcionan suficiente patrón para que intuyas la forma de la gráfica de f, haz el “salto de fe” y traza todos los pares que satisfagan la ecuación que define f dibujando una curva suave en tu sistema de coordenadas. Por supuesto, esta curva debe contener todos los pares previamente trazados.
5. Si tus pares trazados no proporcionan suficiente patrón para determinar la forma final de la gráfica de f, entonces agrega más pares a tu tabla y grácalos en tu sistema de coordenadas cartesianas. Continúa de esta manera hasta que tengas confianza en la forma de la gráfica de f.

Veamos un ejemplo.

Ejemplo\(\PageIndex{1}\)

Dibuje la gráfica de la función definida por la ecuación\(f(x)=x^{3}\).

Solución

Comenzaremos con valores x\(-2,-1,0,1,\) y 2, luego usaremos la ecuación\(f(x)=x^{3}\) para determinar pares (x, f (x)) (e.g.,\(f(-2)=(-2)^{3}=-8\)). Estos se enumeran en la tabla de la Figura\(\PageIndex{7}\) (a). Luego trazamos los puntos de la tabla en un sistema de coordenadas cartesianas, como se muestra en la Figura\(\PageIndex{7}\) (b).

Figura\(\PageIndex{7}\). Trazando pares (x, f (x)) definidos por la ecuación\(f(x)=x^{3}\).

Estamos un poco inseguros de la forma de la gráfica de f, así que agregaremos algunos pares más a nuestra tabla y los trazaremos. Esto se muestra en las Figuras\(\PageIndex{8}\) (a) y (b).

Figura\(\PageIndex{8}\). Trazar pares adicionales (x, f (x)) definidos por la ecuación\(f(x)=x^{3}\).

Los pares adicionales rellenan la forma de f en la Figura\(\PageIndex{8}\) (b) un poco mejor que los de la Figura\(\PageIndex{7}\) (b), lo suficiente para que tengamos la confianza suficiente para dar un “salto de fe” y dibujar la forma final de la gráfica de\(f(x)=x^{3}\) la Figura\(\PageIndex{9}\).

Figura\(\PageIndex{9}\). La gráfica final de\(f(x)=x^{3}\).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{2}\)

Esbozar el gráfico de\(f(x)=\sqrt{x}\)

Solución

Nuevamente, comenzaremos seleccionando varios valores de x en el dominio de f. En este caso\(f(x)=\sqrt{x}\),, y no es posible tomar la raíz cuadrada de un número negativo. Además, si estamos creando una tabla de pares a mano, es una buena estrategia seleccionar cuadrados conocidos. Así, usaremos x = 0, 1, 4 y 9 para empezar.

Figura\(\PageIndex{10}\). Trazando pares (x, f (x)) definidos por la ecuación\(f(x)=\sqrt{x}\).

Algunos podrían estar listos para dar un “salto de fe” basado en estos resultados iniciales. Otros podrían querer usar una calculadora para calcular aproximaciones decimales para raíces cuadradas adicionales. Los pares resultantes se muestran en la tabla de la Figura\(\PageIndex{11}\) (a) y los pares adicionales se representan en la Figura\(\PageIndex{11}\) (b).

Figura\(\PageIndex{11}\) Trazando pares adicionales (x, f (x)) definidos por la ecuación\(f(x)=\sqrt{x}\)

El patrón de la Figura\(\PageIndex{11}\) (b) es lo suficientemente claro como para dar un “salto de fe” y completar la gráfica como se muestra en la Figura\(\PageIndex{12}\).

Figura\(\PageIndex{12}\). La gráfica de f definida por la ecuación\(f(x)=\sqrt{x}\).

Uso de la función de tabla de la calculadora gráfica

La función TABLE en su calculadora gráfica puede ser de inmensa ayuda a la hora de crear tablas de puntos que satisfagan la ecuación que define la función f. Veamos un ejemplo

Ejemplo\(\PageIndex{3}\)

Esbozar el gráfico de\(f(x)=|x|\)

Solución

Ingrese la función\(f(x)=|x|\) en el\(\mathrm{Y}=\) menú de la siguiente manera.

1. Presiona el botón Y= en tu calculadora. Esto abrirá el menú Y= como se muestra en la Figura\(\PageIndex{13}\) (a). Use las teclas de flecha y el botón CLEAR en su calculadora para eliminar cualquier función existente.
2. Pulse el botón MATH para abrir el menú que se muestra en la Figura\(\PageIndex{13}\) (b).
3. Presione la flecha derecha en su calculadora para seleccionar el submenú NUM como se muestra en la Figura\(\PageIndex{13}\) (c).
4. Seleccione 1:abs (, luego ingrese X y cierre los paréntesis, como se muestra en la Figura\(\PageIndex{13}\) (d).

Figura\(\PageIndex{13}\). Entrando\(f(x)=|x|\) en el\(\mathrm{Y}=\) menú.

Ahora utilizaremos la función TABLE de la calculadora gráfica para ayudar a crear una tabla de pares (x, f (x)) que satisfaga la ecuación\(f(x) = |x|\). Proceder de la siguiente manera.

1. Seleccione 2do TBLSET (es decir, presione el segundo botón seguido de TBLSET), que se encuentra sobre el botón VENTANA. Ingrese tblStart=-3,\(\Delta \mathrm{Tb} 1=1\), y establezca las variables independientes y dependientes en Auto (esto se hace resaltando Auto y presionando el botón Enter), como se muestra en la Figura\(\PageIndex{14}\) (a).
2. Presione 2da TABLACIÓN, que se encuentra encima del botón GRAPADO, para producir la tabla de pares (x, f (x)) que se muestra en la Figura\(\PageIndex{14}\) (b).

Hemos trazado los pares directamente desde la calculadora sobre un sistema de coordenadas cartesianas en papel cuadriculado en la Figura\(\PageIndex{14}\) (c).

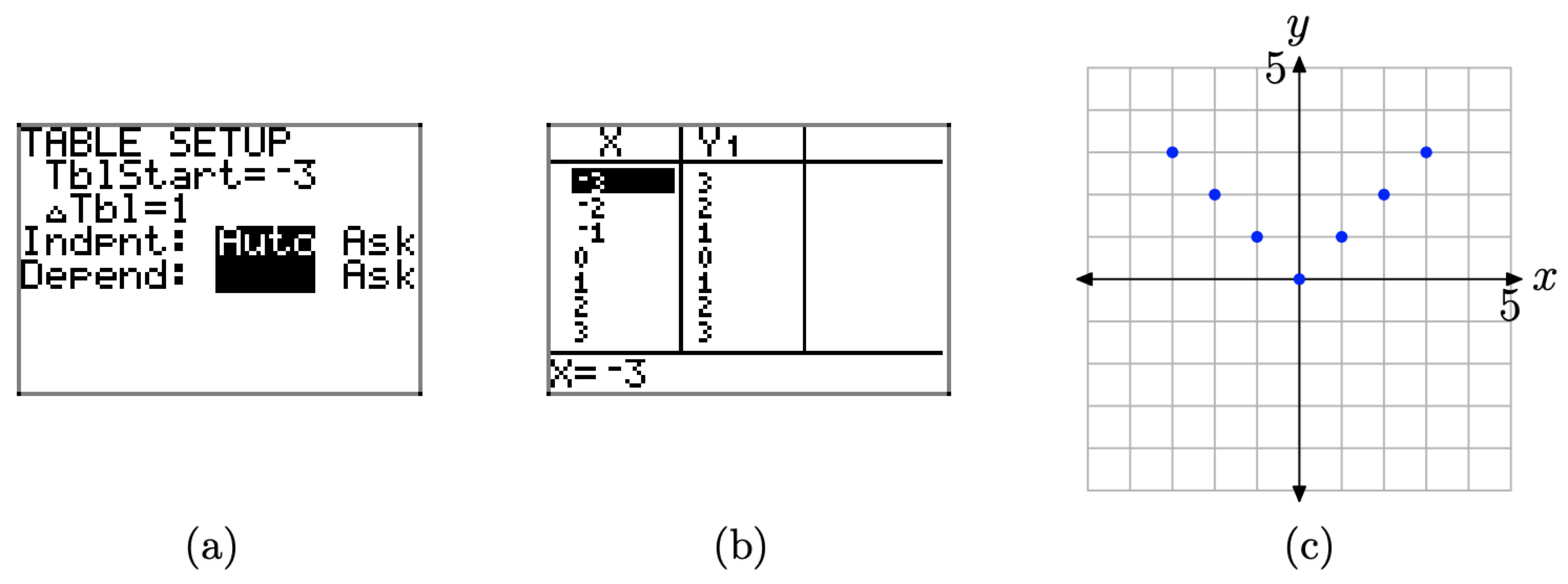
Figura\(\PageIndex{14}\). Crear una tabla con la función TABLE de la calculadora gráfica.

A partir de lo que vemos en la Figura\(\PageIndex{14}\) (c), estamos listos para dar un “salto de fe” y dibujar la gráfica de f que se muestra en la Figura\(\PageIndex{15}\).

Figura\(\PageIndex{15}\). La gráfica de f definida por\(f(x) = |x|\).

Alternativamente, o como cheque, podemos hacer que la calculadora gráfica dibuje la gráfica para nosotros. Presione el botón ZOOM, luego seleccione 6:ZStandard (mostrado en la Figura\(\PageIndex{16}\) (a)) para producir la gráfica que se muestra en la Figura\(\PageIndex{16}\) (b).

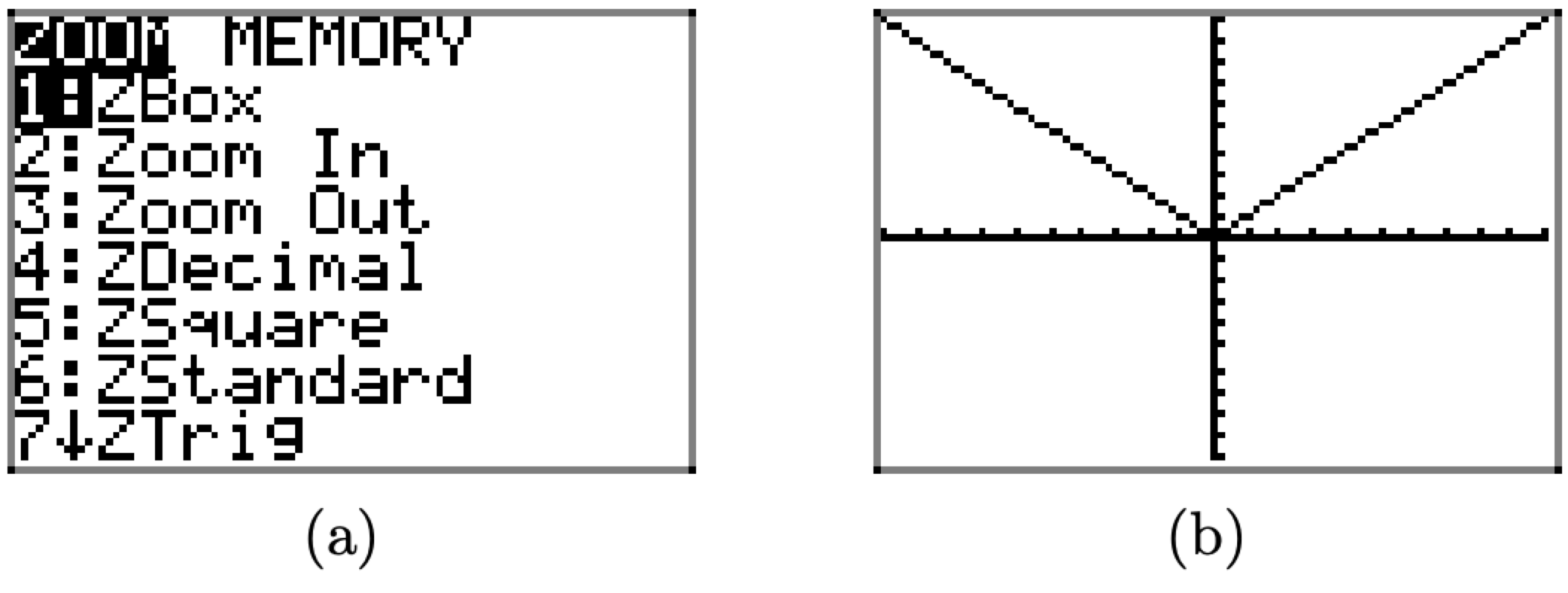
Figura\(\PageIndex{16}\). Creando la gráfica de\(f(x) = |x|\) con la calculadora gráfica.

Ajuste de la ventana de visualización

En Ejemplo\(\PageIndex{3}\), se utilizó la calculadora gráfica para dibujar la gráfica de la función definida por la ecuación\(f(x) = |x|\). Para las funciones que hemos encontrado hasta ahora, dibujar sus gráficas usando la calculadora gráfica es bastante trivial. Simplemente ingrese la ecuación en el menú Y=, luego presione el botón ZOOM y seleccione 6:ZStandard. Sin embargo, si la gráfica de una función no encaja (o incluso aparece) en la ventana de visualización “estándar”, puede ser bastante difícil encontrar configuraciones de vista óptimas para que las características importantes de la gráfica sean visibles.

De hecho, como uno podría ni siquiera saber qué características “importantes” buscar, configurar la ventana de visualización suele ser altamente subjetivo y experimental por naturaleza. Veamos algunos ejemplos.

Ejemplo\(\PageIndex{4}\)

Utilice una calculadora gráfica para bosquejar el gráfico de\(f(x)=56-x-x^{2}\). Experimente con los ajustes de VENTANA hasta que sienta que tiene una ventana de visualización que exhiba las características importantes de la gráfica.

Solución

Primero, comience ingresando la función en el menú Y=, como se muestra en la Figura\(\PageIndex{17}\) (a). El caret en el teclado se utiliza para exponentes. Pulse el botón ZOOM y seleccione 6:ZStandard para producir la gráfica que se muestra en la Figura\(\PageIndex{17}\) (b).

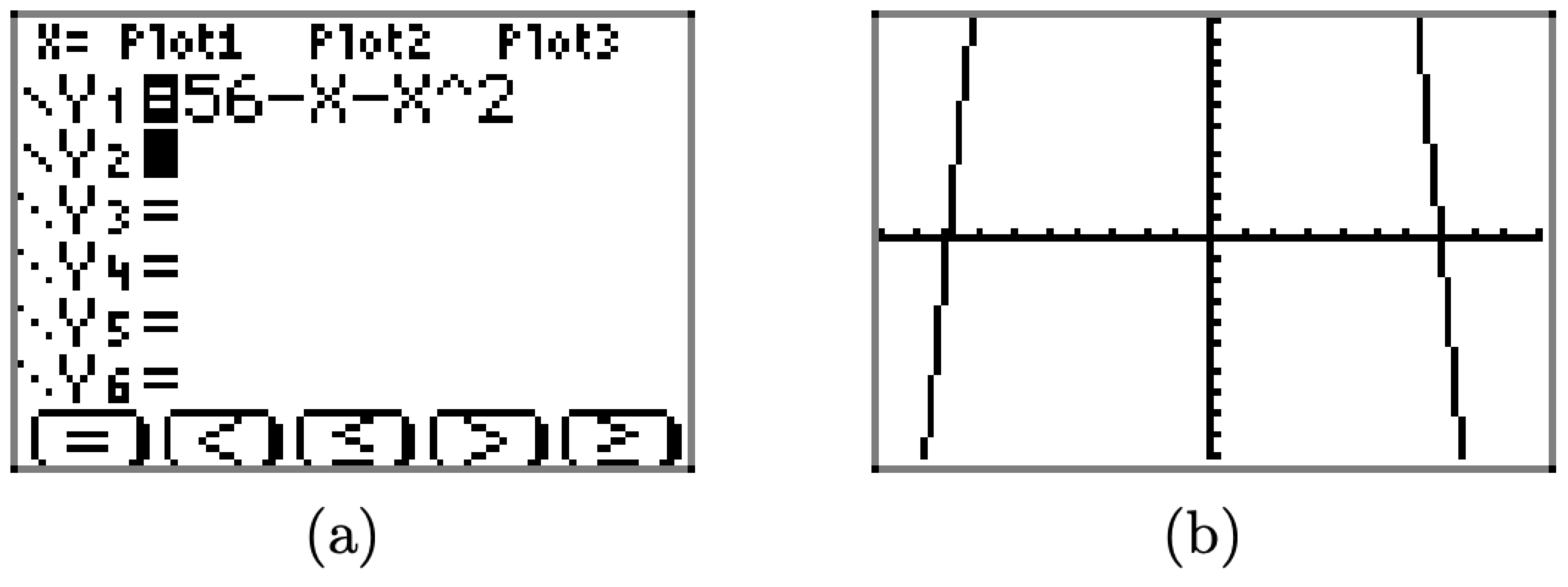
Figura\(\PageIndex{17}\). La gráfica de\(f(x)=56-x-x^{2}\) en la ventana de visualización “estándar”.

A medida que dibuja la gráfica, observe que la gráfica se eleva desde la parte inferior de la pantalla, sale de la parte superior de la pantalla, luego regresa, cayendo desde la parte superior de la pantalla y dejando de nuevo en la parte inferior de la pantalla. Esto indicaría que debe haber algún tipo de “punto de inflexión” que no sea visible en la parte superior de la pantalla.

Presione el botón VENTANA para mostrar la configuración de la “ventana de visualización estándar” que se muestra en la Figura\(\PageIndex{18}\) (a). La siguiente leyenda explica cada uno de los parámetros WINDOW en la Figura\(\PageIndex{18}\) (a).

\ (\ begin {array} {lll} Xmin & =& x-value del borde izquierdo de la ventana de visualización\\

Xmax &=& valor x del borde derecho de la ventana de visualización\\

Xscl &=& incremento de tick del eje x\\

Y min &=& valor y del borde inferior de la ventana de visualización\\

Y max &=& valor y del borde superior de la ventana de visualización\\

Y scl &=& incremento de tick del eje y\ end {array}\)

Es fácil evaluar la función\(f(x)=56-x-x^{2}\) en\(x = 0\). Efectivamente,\(f(0) = 56−0−0^2 = 56\). Esto indica que la gráfica de f debe pasar por el punto (0, 56). Esto nos da una pista de cómo debemos establecer el límite superior en nuestra ventana de visualización. Establezca Ymax = 60, como se muestra en la Figura\(\PageIndex{18}\) (b), luego presione el botón GRAPADO para producir la gráfica y la ventana de visualización que se muestra en la Figura\(\PageIndex{18}\) (c).

Figura\(\PageIndex{18}\). Cambiar la ventana de visualización.

Si bien la ventana de visualización en la Figura\(\PageIndex{18}\) (c) muestra el “punto de inflexión” de la gráfica de f, realizaremos algunos cambios adicionales en la configuración de la ventana, como se muestra en la Figura\(\PageIndex{19}\) (a). Primero, “ampliamos” un poco la ventana de visualización, configurando Xmin = -15 y Xmax = 15, luego colocamos marcas de verificación en el eje x cada 5 unidades con Xscl = 5. A continuación, para crear un pequeño espacio en la parte superior de la pantalla, establecemos Ymax = 100, luego “equilibramos” esta configuración con Ymin = -100. Finalmente, establecemos marcas de verificación en el eje y cada 10 unidades con Yscl = 10.

Pulse el botón GRAPH para ver los efectos de estos cambios en los parámetros WINDOW en la Figura\(\PageIndex{19}\) (b). Tenga en cuenta que estos ajustes son altamente subjetivos, y lo que un lector puede encontrar bastante agradable no necesariamente encontrará favor con otros lectores.

No obstante, lo importante es el hecho de que hemos capturado las “características importantes” de la gráfica de\(f(x)=56-x-x^{2}\). Tenga en cuenta que se trata de una declaración muy polémica. Si uno apenas comienza a aprender sobre las gráficas de funciones, ¿cómo se puede determinar cuáles son las “características importantes” de la gráfica? Desafortunadamente, la respuesta a esta pregunta es, “a través de la experiencia”. Sin duda, esta es una frase muy frustrante para que los lectores la escuchen, pero al menos es veraz. Cuantas más gráficas dibujes, más aprenderás a buscar “puntos de inflexión”, “comportamiento final”, “intercepciones x e y”, y similares.

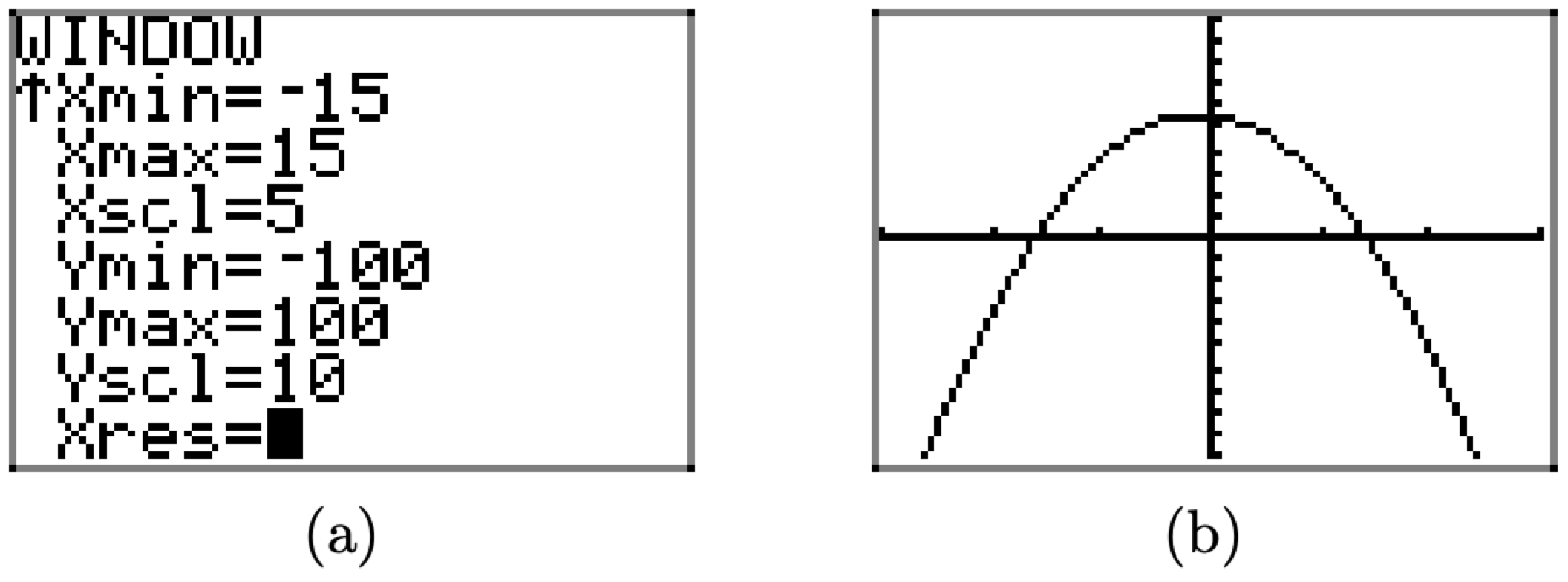
Figura\(\PageIndex{19}\). Mejorando la configuración de VENTANA.

Por ejemplo, ¿cómo sabemos que los ajustes de VENTANA en la Figura\(\PageIndex{19}\) (a) determinan una ventana de visualización (Figura\(\PageIndex{19}\) (b)) que revela todas las “características importantes” de la gráfica? La respuesta en este punto es, “no lo hacemos, no sin más experimentos”. Por ejemplo, el lector cuidadoso podría querer probar los ajustes de la ventana Xmin=-50, Xmax=50, Xscl=10, Ymin=-500, Ymax=500 e Ysc=100 para ver si surge algún comportamiento inesperado.

Veamos un último ejemplo.

Ejemplo\(\PageIndex{5}\)

Dibuje la gráfica de la función f definida por la ecuación\(f(x) = x^{4}+9 x^{3}-117 x^{2}-265 x+2100\).

Solución

Cargue la función en el menú Y= (mostrado en la Figura\(\PageIndex{20}\) (a)) y seleccione 6:ZStandard para producir la gráfica que se muestra en la Figura\(\PageIndex{20}\) (b).

Figura\(\PageIndex{20}\) Dibujando la gráfica de\(f(x) = x^{4}+9 x^{3}-117 x^{2}-265 x+2100\).

A medida que se dibuja la gráfica, observe que se eleva desde la parte inferior de la ventana de visualización, sale de la parte superior de la ventana de visualización, luego vuelve a caerse de la parte inferior de la ventana de visualización, luego regresa nuevamente y se eleva por la parte superior de la ventana de visualización.

Notamos que f (0) = 2100, por lo que tendremos que establecer la parte superior de la ventana de visualización a ese valor o superior. Con este pensamiento en mente, estableceremos Ymax=3000, luego estableceremos Ymin=-3000 para el saldo, luego para evitar un millón de pequeñas marcas, estableceremos Ysc=1000, todo mostrado en la Figura\(\PageIndex{21}\) (a). Al pulsar el botón GRAPH se produce entonces la imagen que se muestra en la Figura\(\PageIndex{21}\) (b).

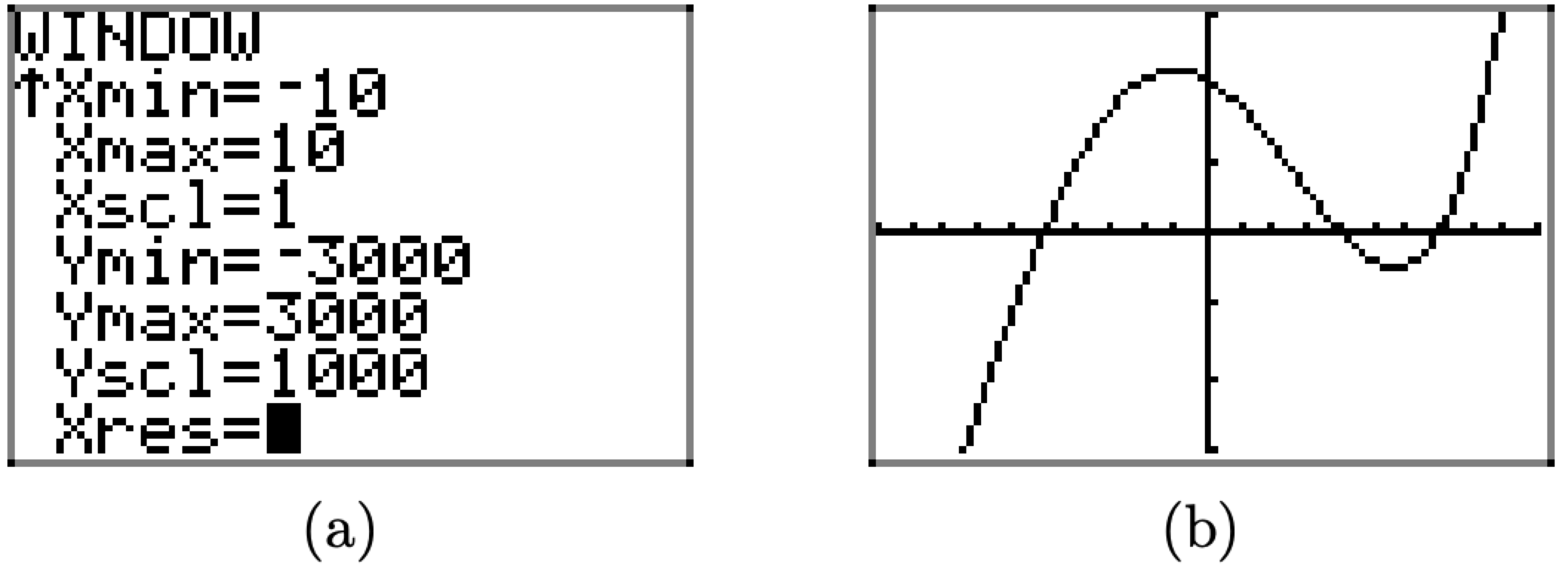
Figura\(\PageIndex{21}\) Ajuste de la ventana de visualización.

¿Parece que tenemos todas las “características importantes” de esta gráfica mostradas en nuestra ventana de visualización? Tenga en cuenta que no experimentamos mucho. Quizás deberíamos intentar ampliar un poco más la ventana para ver si nos hemos perdido algún comportamiento importante. Con ese pensamiento en mente, establecemos Xmin=-20, Xmax=20, y para evitar un montón de marcas de verificación, Xscl=5, como se muestra en la Figura\(\PageIndex{22}\) (a). Al presionar el botón GRAPH se obtiene la imagen en la Figura\(\PageIndex{22}\) (b).

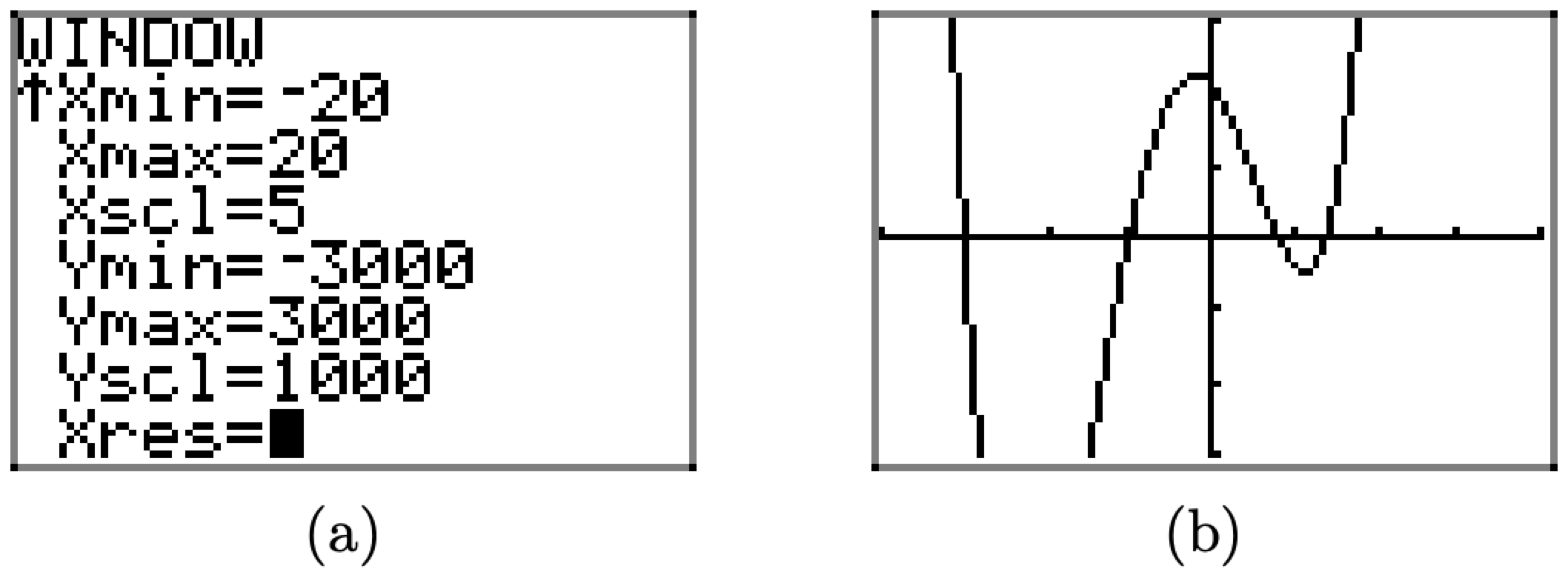
Figura\(\PageIndex{22}\) Ajustar de nuevo la ventana de visualización revela un comportamiento no visto.

Obsérvese que la ventana de visualización en la Figura\(\PageIndex{22}\) (b) revela un comportamiento no visto en la ventana de visualización de la Figura\(\PageIndex{21}\) (b). Si no hubiéramos experimentado más, si no hubiéramos ampliado la ventana de visualización, no habríamos visto este nuevo comportamiento. Esta es una lección importante.

Tenga en cuenta que uno de los “puntos de inflexión” de la gráfica en la Figura\(\PageIndex{22}\) (b) se encuentra fuera de la parte inferior de la ventana de visualización. Haremos un ajuste más para incluir esta importante característica. Establezca Ymin=-10000, Ymax=10000 e Ysc=5000, como se muestra en la Figura\(\PageIndex{23}\) (a), luego presione el botón GRAPH para producir la imagen mostrada en la Figura\(\PageIndex{23}\) (b).

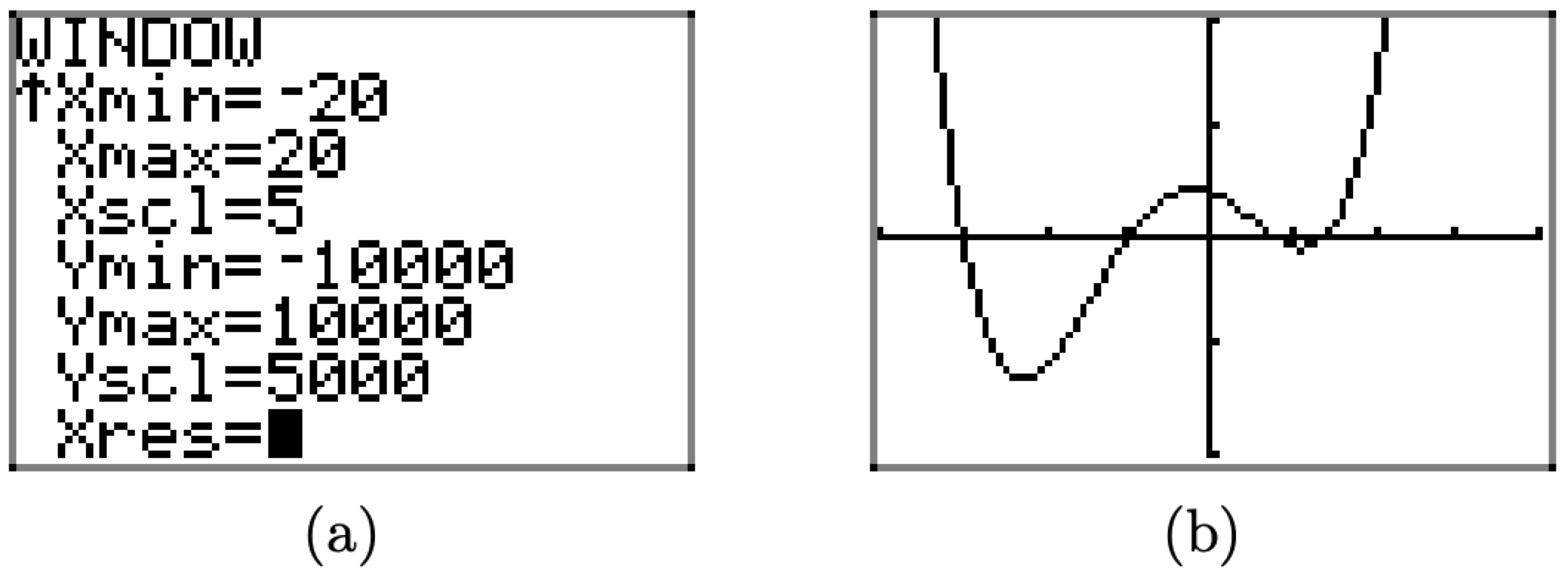
Figura\(\PageIndex{23}\). Ajustar nuevamente la ventana de visualización revela un comportamiento no visto.

La gráfica de la Figura\(\PageIndex{23}\) (b) muestra todas las “características importantes” de la gráfica de f, pero el lector cuidadoso continuará experimentando, ampliando la ventana de visualización para conocer la verdad de esta afirmación.