3.1: Modelos Lineales
- Page ID
- 110768
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sebastián se despide de su hermano, quien está platicando con un grupo de sus amigos aproximadamente a 20 pies de distancia. Entonces Sebastián comienza a alejarse de su hermano a un ritmo constante de 4 pies por segundo. Modelaremos la distancia que separa a los dos hermanos en función del tiempo.
Nuestro primer acercamiento será gráfico. Dejaremos que la variable d represente la distancia (en pies) entre los hermanos y la variable t represente la cantidad de tiempo (en segundos) que ha pasado desde que Sebastián se despidió de su hermano. Debido a que la distancia que separa a los hermanos depende de la cantidad de tiempo que haya pasado, diremos que la distancia d es la variable dependiente y el tiempo t es la variable independiente.
Es algo tradicional en el proceso de modelado colocar la variable independiente en el eje horizontal y la variable dependiente en el eje vertical. Esta no es una regla dura y rápida, más una cuestión de gusto personal, pero seguiremos esta regla en nuestro ejemplo no obstante. De esta manera, colocaremos la distancia en el eje vertical y el tiempo en el eje horizontal, como se muestra en la Figura\(\PageIndex{1}\). Observe que hemos etiquetado cada eje con su representación variable e incluido las unidades, una práctica importante.
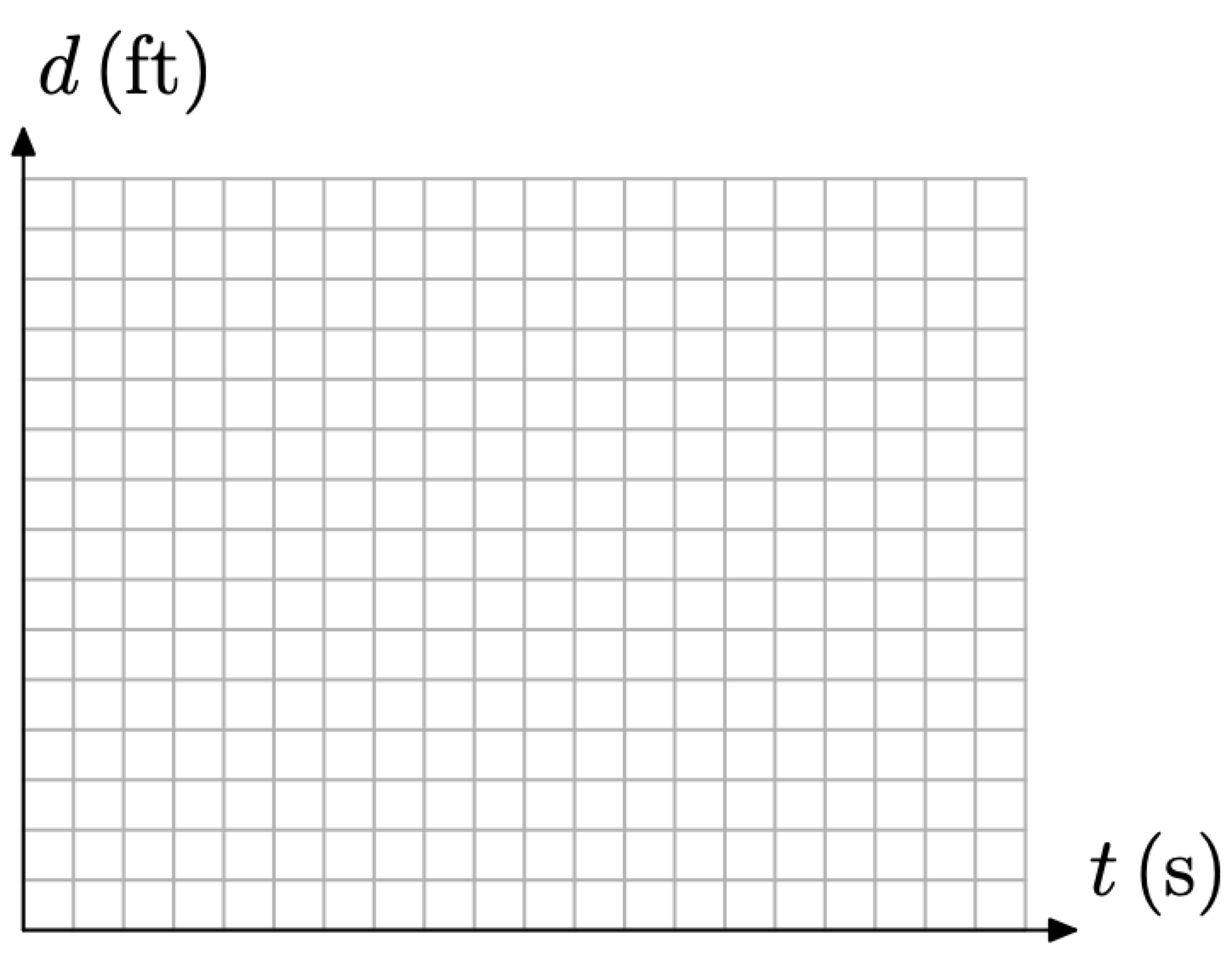
Figura\(\PageIndex{1}\). La distancia depende del tiempo.
Advertencia
La etiqueta en el eje horizontal, t (s), podría parecer notación de función para algunos lectores. Este no es el caso. Más bien, la variable t representa el tiempo, y la (s) entre paréntesis que sigue representa segundos, una abreviatura estándar en física. Comentarios similares están en orden para la etiqueta d (ft). La variable d representa la distancia, y la (ft) entre paréntesis que sigue representa pies, otra abreviatura estándar en física.
Hay varias maneras diferentes en las que puedes etiquetar los ejes de tu gráfica con unidades apropiadas para el problema en cuestión. Por ejemplo, considere la técnica presentada en la Figura\(\PageIndex{2}\), donde las etiquetas se colocan a la izquierda del eje vertical y debajo del eje horizontal. Otra diferencia es el hecho de que las abreviaturas unitarias de la Figura 1 se detallan en su totalidad en la Figura\(\PageIndex{2}\).
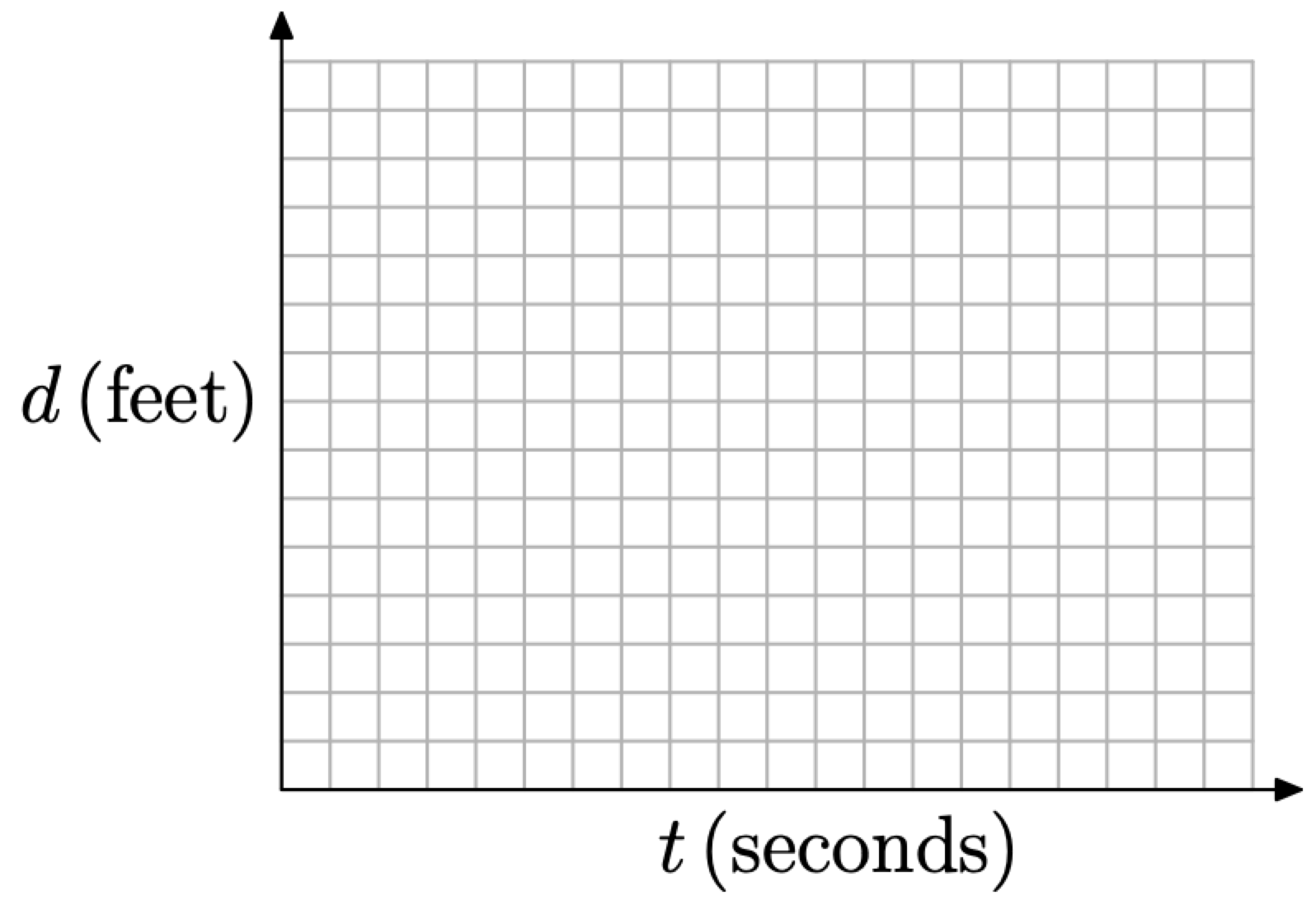
Figura\(\PageIndex{2}\). La distancia depende del tiempo.
Algunos instructores prefieren que rotes la etiqueta de distancia sobre el eje vertical noventa grados, para que aparezca de lado. Otros prefieren que etiquetes los extremos de cada eje con la variable, como lo hemos hecho en Figura\(\PageIndex{1}\), pero deletrear las unidades en su totalidad a lo largo de cada eje como lo hemos hecho en la Figura\(\PageIndex{2}\). La lista de preferencias sigue y sigue.
Nota
Es importante tener una conversación con tu instructor para determinar cuáles son las expectativas de tu instructor a la hora de etiquetar los ejes e indicar las unidades en tus gráficas.
Preferimos etiquetar los ejes como se muestra en la Figura\(\PageIndex{1}\), e intentaremos ser consistentes con este estándar a lo largo del resto del texto, aunque podríamos desviarnos a formas alternas de etiquetado de vez en cuando
Ahora debemos escalar cada eje de manera apropiada, una tarea que es más difícil de lo que parece en primer lugar. Una mala elección de escala puede hacer que la tarea por delante sea más difícil de lo que debe ser. Escogeremos una escala para cada eje con los siguientes pensamientos en mente.
Lineamientos para Escalar Ejes
Aquí hay algunos buenos consejos a seguir al escalar los ejes dependientes e independientes.
- Queremos evitar las gráficas del tamaño de un sello postal. Un gráfico grande es más fácil de interpretar que uno que está abarrotado en un pequeño rincón de nuestro papel cuadriculado.
- No es necesario tener la misma escala en cada eje, pero una vez que se elige una escala, debes seguir siendo consistente.
- Queremos elegir una escala que se correlacione fácilmente con la tasa dada.
Sebastián se aleja de su hermano a un ritmo constante de 4 pies por segundo. Dejemos que cada cuadro en el eje vertical represente 4 pies y cada dos cajas en el eje horizontal representen 1 segundo, como se muestra en la Figura\(\PageIndex{3}\).
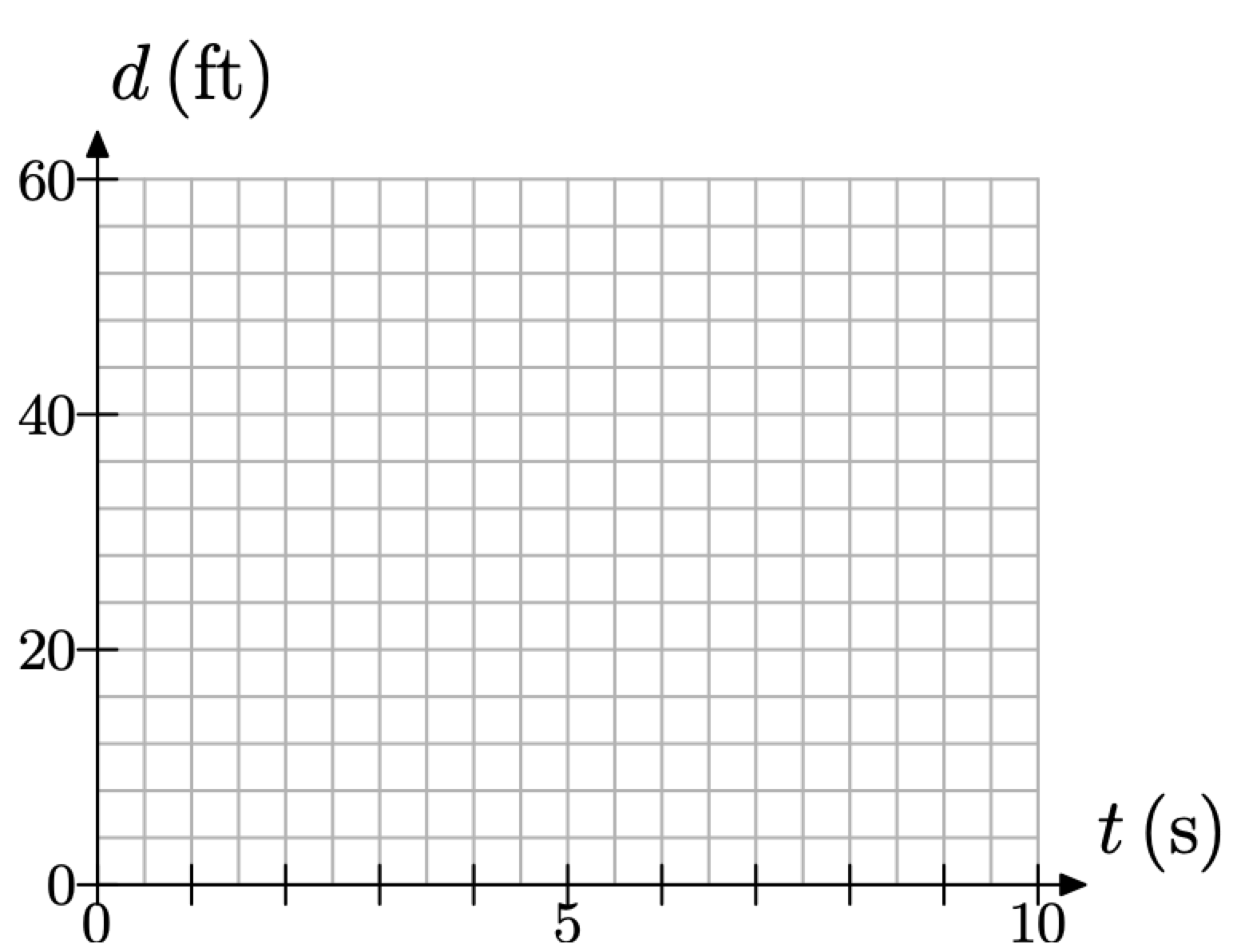
Figura\(\PageIndex{3}\). Escalando cada eje para acomodar la velocidad.
En el tiempo t = 0, Sebastián está separado de su hermano por una distancia de d = 20 pies. Esto corresponde al punto (t, d) = (0, 20) mostrado en la Figura\(\PageIndex{4}\) (a).
A continuación, Sebastián se aleja de su hermano a un ritmo constante de 4 pies por segundo. Esto quiere decir que por cada segundo de tiempo que transcurre, la distancia entre los hermanos aumenta en 4 pies. Comenzando en el punto (0, 20), mover 1 segundo (dos cajas) a la derecha y 4 pies (1 caja) hacia arriba hasta el punto (1, 24), como se muestra en la Figura\(\PageIndex{4}\) (b).
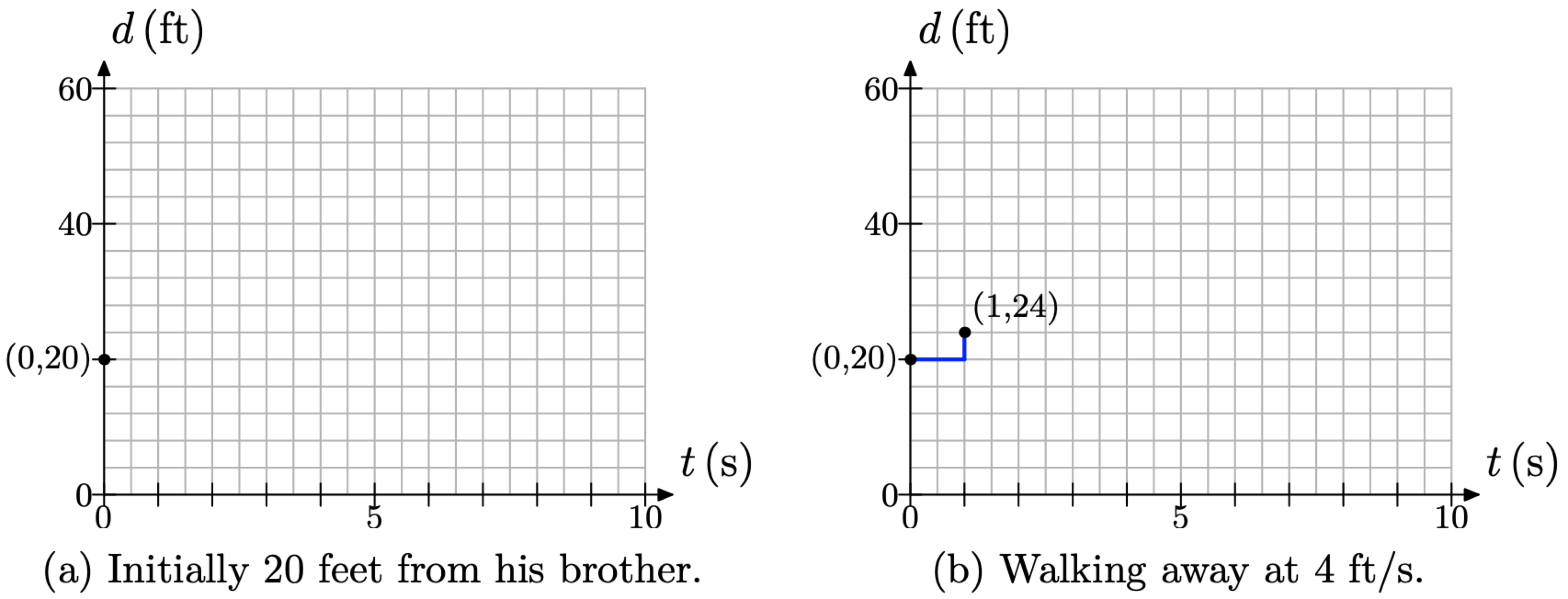
Figura\(\PageIndex{4}\).
La velocidad de separación es constante de 4 pies por segundo. Entonces, continuar indefinidamente a la manera de la Figura Figura\(\PageIndex{4}\) (b), moviendo 1 segundo (2 cajas) hacia la derecha, luego 4 pies hacia arriba (1 caja). Esto producirá la relación lineal entre distancia y tiempo sugerida en la Figura\(\PageIndex{5}\) (a).
Si asumimos que la distancia es una función continua del tiempo, una suposición legítima debido a que la distancia está aumentando continuamente a una velocidad constante de 4 pies por segundo, entonces podemos reemplazar el conjunto discreto de puntos de datos de la Figura\(\PageIndex{5}\) (a) con la línea que se muestra en la Figura\(\PageIndex{5}\) (b).
La línea de la Figura\(\PageIndex{5}\) (b) es un modelo continuo. Se puede dibujar con un simple trazo del lápiz, sin que la punta del lápiz deje nunca contacto con nuestro papel cuadriculado. Por otro lado, el conjunto de puntos en la Figura\(\PageIndex{4}\) (a) es un modelo discreto. Después de trazar un punto, nuestro lápiz debe romper el contacto con nuestro papel cuadriculado antes de trazar el siguiente punto. Esta es la diferencia esencial entre un modelo discreto y un modelo continuo.
En este caso, el modelo continuo es una representación más precisa de la distancia entre los hermanos. Decimos esto porque la distancia entre ellos está aumentando a un ritmo constante de 4 pies por segundo, o 2 pies cada medio segundo, o 1 pie cada cuarto de segundo, etc. En breve, mostraremos un ejemplo donde este tipo de modelo continuo no es razonable.
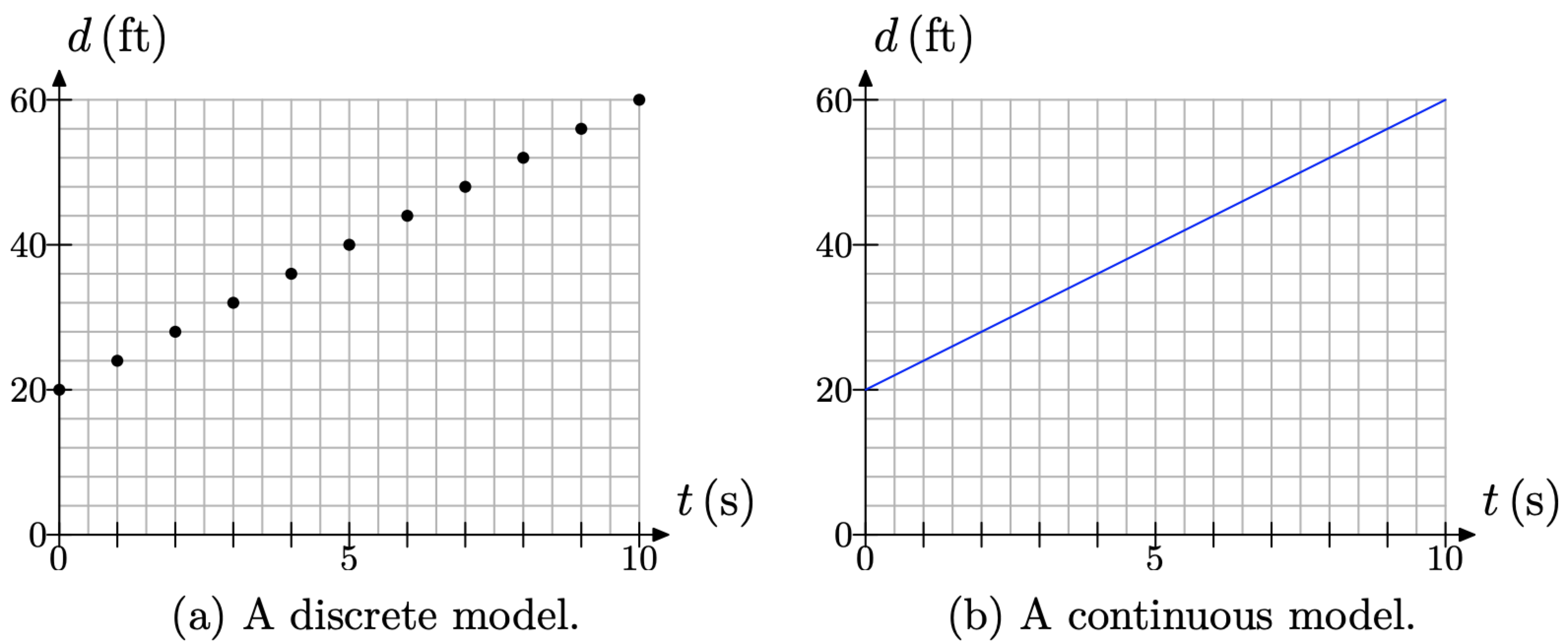
Figura\(\PageIndex{5}\). La tasa constante produce una relación lineal.
Ahora que hemos modelado la distancia entre los hermanos con una gráfica, podemos usar la gráfica para hacer predicciones. Por ejemplo, para determinar la distancia entre los hermanos después de 8 segundos, ubique 8 segundos en el eje de tiempo, dibuje una flecha vertical a la línea, luego una flecha horizontal al eje de distancia, como se muestra en la Figura\(\PageIndex{6}\).
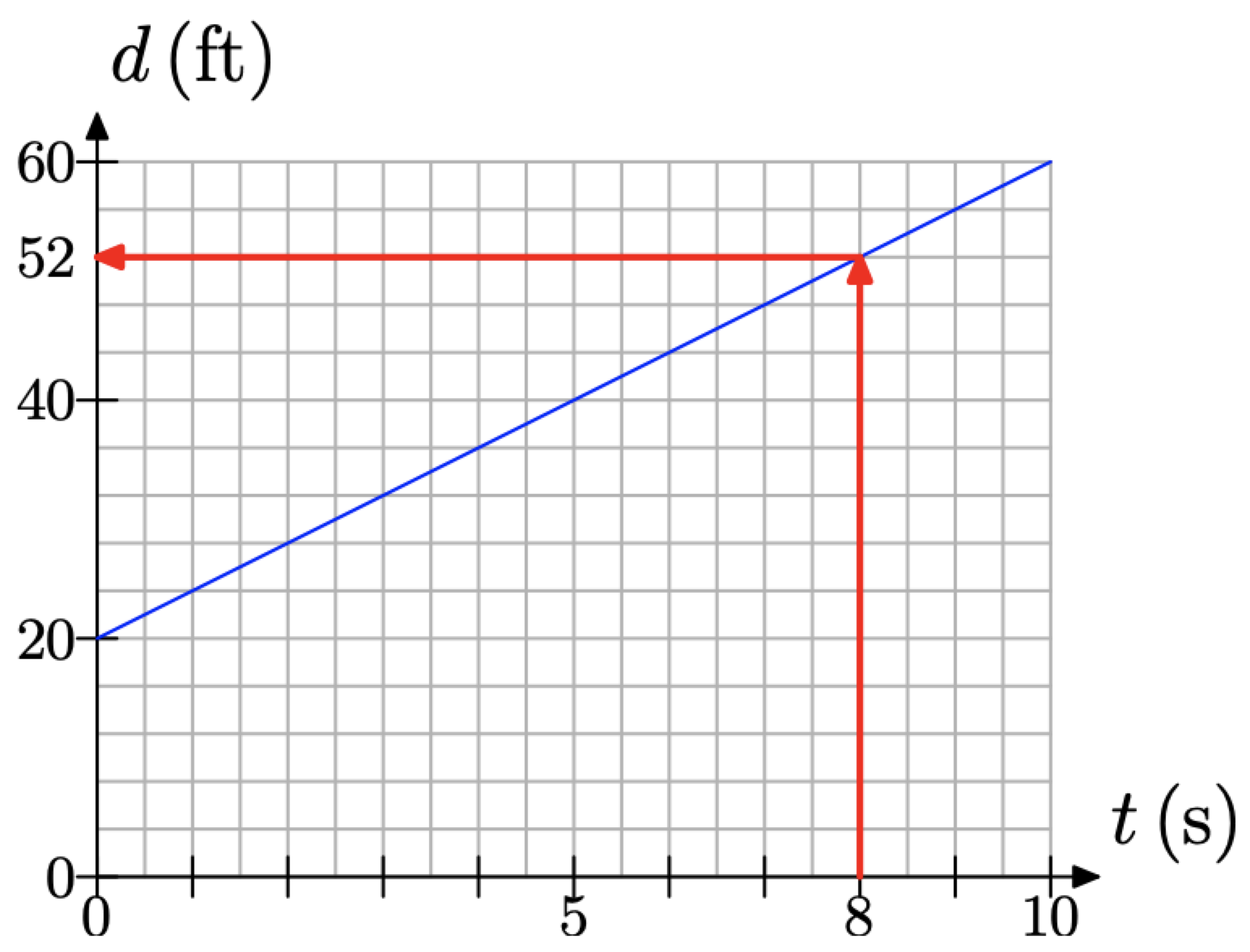
Figura\(\PageIndex{6}\). Predecir la distancia entre los hermanos después de 8 segundos.
No obstante, supongamos que queremos determinar la distancia entre los hermanos después de 2 minutos. Como la gráfica de la Figura\(\PageIndex{5}\) (b) solo modela la distancia a lo largo de los primeros 10 segundos, tendríamos que volver a dibujar la gráfica durante los primeros 2 minutos (120 segundos) para determinar la respuesta. No planeamos con anticipación para esta contingencia, así que quizás podamos modelar la distancia entre los hermanos de otra manera, una que prediga más fácilmente la distancia entre los hermanos después de una cantidad arbitraria de tiempo t.
Para ello, se busca un patrón que describa la distancia d entre los hermanos en función del tiempo t. Debido a que la distancia entre los hermanos está aumentando a una velocidad de 4 pies por segundo, observamos que:
- A t = 0 segundos, la distancia entre los hermanos es d = 20 pies.
- A t = 1 segundo, la distancia entre los hermanos es d = 24 pies.
- A t = 2 segundos, la distancia entre los hermanos es d = 28 pies.
- A t = 3 segundos, la distancia entre los hermanos es d = 32 pies.
Resumimos estos resultados en la Tabla\(\PageIndex{1}\) (a).
Sin embargo, no se quiere simplificar las distancias como tenemos en la Tabla\(\PageIndex{1}\) (a), porque oculta el patrón o la relación entre la distancia d y el tiempo t Es más eficiente buscar una relación entre distancia y tiempo de la siguiente manera. Después de t = 1 segundo, la distancia aumenta en 1 incremento de 4 pies, por lo que d = 20 + 4 (1). Después de t = 2 segundos, la distancia aumenta en 2 incrementos de 4 pies, por lo que d = 20 + 4 (2). Continuando de esta manera, tenemos:
• A t = 3 segundos, la distancia entre los hermanos es d = 20 + 4 (3) pies.
• A t = 4 segundos, la distancia entre los hermanos es d = 20 + 4 (4) pies.
Estos resultados se resumen en la Tabla\(\PageIndex{1}\) (b).
| t | d |
|---|---|
| 0 | 20 |
| 1 | 24 |
| 2 | 28 |
| 3 | 32 |
Tabla\(\PageIndex{1}\) (a) Determinación de una ecuación modelo.
| t | d |
|---|---|
| 0 |
20 |
| 1 | 20 + 4 (1) |
| 2 | 20 + 4 (2) |
| 3 | 20 + 4 (3) |
Cuadro\(\PageIndex{1}\) (b) Determinación de una ecuación modelo.
A diferencia de la Tabla\(\PageIndex{1}\) (a), la Tabla\(\PageIndex{1}\) (b) revela una relación entre la distancia d y el tiempo t que puede ser descrita por la ecuación
\[d=20+4 t\]
El lector cuidadoso verificará que la ecuación (3) revele las distancias correctas para t = 0, 1, 2 y 3 segundos, como se registra en la Tabla\(\PageIndex{1}\) (a). Se pueden hacer dos observaciones importantes sobre la ecuación (3).
- El 20 en d = 20 + 4t es la distancia inicial entre los hermanos y corresponde al punto (0, 20) de la Figura\(\PageIndex{4}\) (a).
- El 4 en N = 20 + 4t es la velocidad a la que aumenta la distancia entre los hermanos (4 pies por segundo).
Además, la ecuación (3) se puede utilizar para predecir la distancia entre los hermanos a los 2 minutos. Primero, convierta t = 2 minutos a t = 120 segundos, luego sustituya este número en nuestra ecuación modelo (3).
\[d=20+4(120)=500\]
Así, la distancia entre los hermanos después de 2 minutos es d = 500 pies.
También podemos escribir la ecuación d = 20 + 4t usando notación de funciones.
\[d(t)=20+4 t\]
Entonces, para encontrar la distancia entre los hermanos al cabo de 2 minutos, realizaríamos el siguiente cálculo.
\[\begin{array}{l}{d(120)=20+4(120)} \\ {d(120)=500}\end{array}\]
A diferencia de la notación de funciones, cuando el resultado se escribe d = 500 pies, observe cómo se oculta una pieza de información, es decir, el tiempo. Con notación de función, interpretamos d (120) = 500 para significar “la distancia entre los dos hermanos después de 120 segundos es de 500 pies”. Observe cómo tanto la distancia como el tiempo están disponibles en la notación d (120) = 500.
Modelado del Discreto con el Continuo
Jenny construye una conejera detrás de su granero. Ella coloca 25 conejos en la conejera, luego cierra la puerta y se va. Desafortunadamente, existe una falla en el diseño de la conejera y los conejos comienzan a escapar a un ritmo constante de 5 conejos cada 2 horas. Nuevamente, modelaremos el número N de conejos que quedan en la conejera en función del tiempo t. Primero, proponemos un modelo gráfico.
Tenga en cuenta que el número de conejos que quedan en la conejera depende de la cantidad de tiempo que haya pasado. Esto hace que el número N de conejos que quedan en la conejera sea la variable dependiente, la cual colocaremos en el eje vertical en la Figura\(\PageIndex{7}\) (a). El tiempo t es la variable independiente y se coloca en el eje horizontal.
Nuevamente elegiremos una escala para nuestros ejes que acomode el hecho de que la población de conejos está disminuyendo a un ritmo constante de 5 conejos cada 2 horas. En la Figura\(\PageIndex{7}\) (b), dejamos que cada caja en el eje vertical represente 1 conejo, mientras que dos cajas en el eje horizontal representan 1 hora. Con la misma facilidad podríamos dejar que cada cuadro en el eje horizontal represente una hora, pero nuestra elección hace una gráfica que es un poco más grande. Los gráficos más grandes son un poco más fáciles de leer e interpretar.
En el tiempo t = 0 horas, la población de conejos es N = 25 conejos. Este hecho está representado por el punto (t, N) = (0, 25) en la Figura\(\PageIndex{8}\) (a). Debido a que la población de conejos disminuye a un ritmo constante de 5 conejos cada 2 horas, comenzamos en el punto (0, 25), luego nos movemos 2 horas (4 cajas) a la derecha, y 5 conejos (5 cajas) hacia abajo al punto (2, 20), también se muestra en la Figura\(\PageIndex{8}\) (a).
La velocidad a la que los conejos están disminuyendo es constante a 5 conejos cada 2 horas, por lo que continuar indefinidamente a la manera de la Figura\(\PageIndex{8}\) (a), moviéndose 2 horas (4 cajas) hacia la derecha, luego 5 conejos (5 cajas) hacia abajo. Esto producirá la relación lineal entre el número de conejos N y el tiempo t mostrado en la Figura\(\PageIndex{8}\) (b).

Figura\(\PageIndex{7}\).
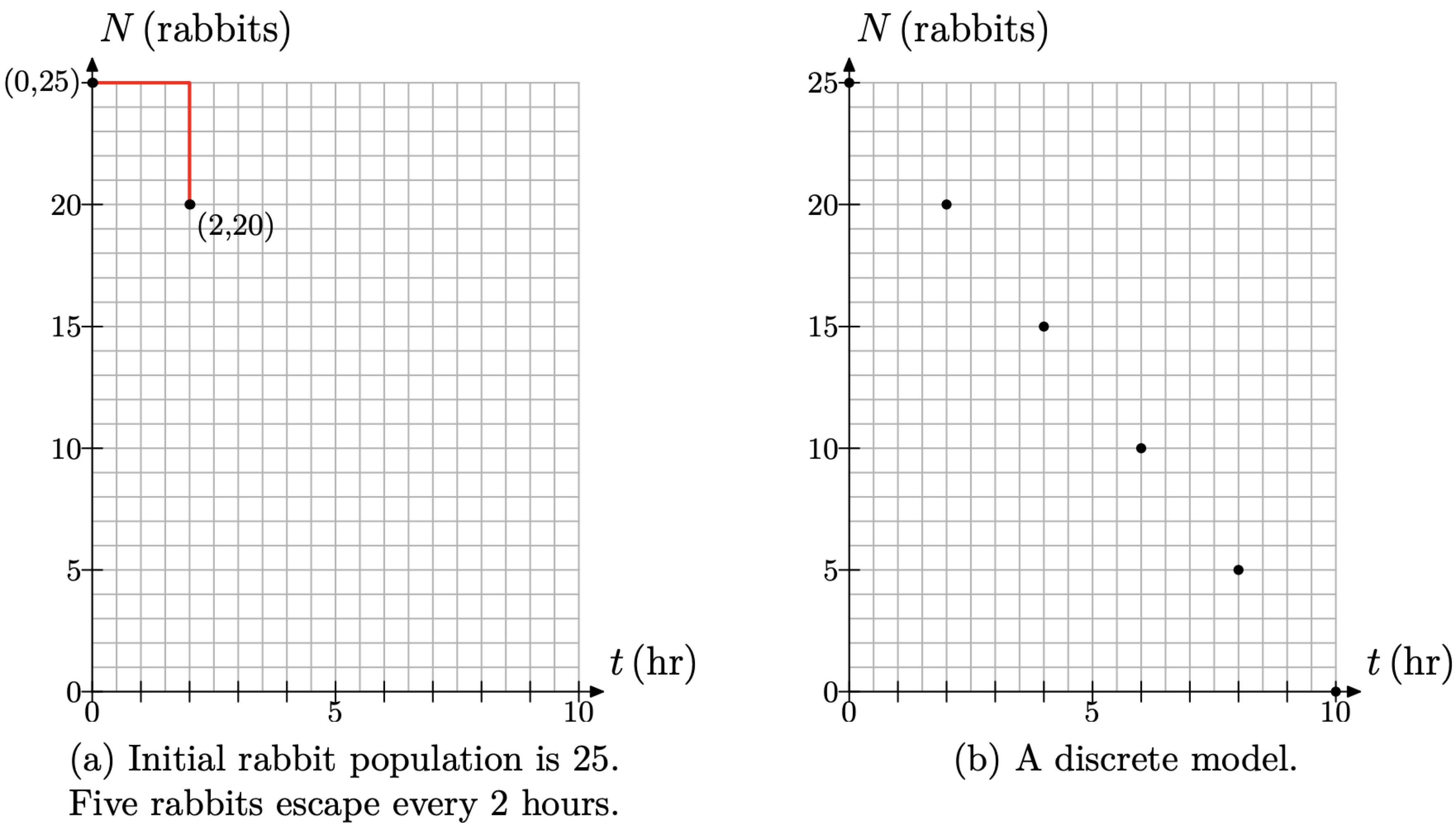
Figura\(\PageIndex{8}\).
Podemos trazar una línea a través de los puntos de datos de la Figura\(\PageIndex{8}\) (b) para producir el modelo continuo en la Figura\(\PageIndex{9}\) (a). No obstante, hay que ser conscientes de la carencia que impone esta aproximación continua. Por ejemplo, considere la predicción en la Figura\(\PageIndex{9}\) (b). ¿Es razonable decir que quedan 7.5 conejos en la conejera después de 7 horas?
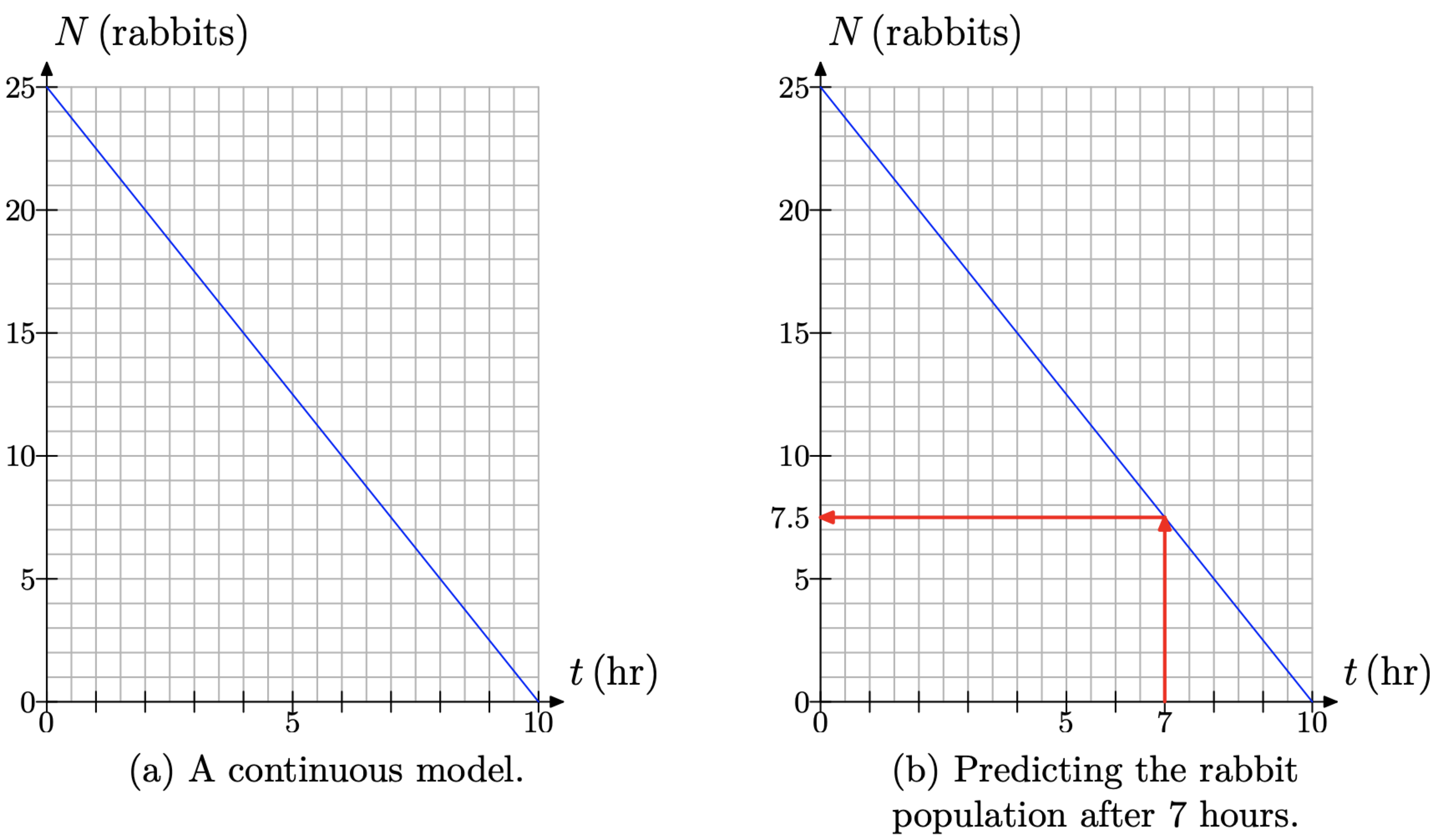
Figura\(\PageIndex{9}\).
En nuestro primer modelo, la distancia entre los hermanos puede ser cualquier número real, por lo que un modelo continuo fue apropiado. Sin embargo, en el caso de la conejera de Jenny, la población restante debe ser un número entero de conejos (a menos que entre un zorro), por lo que modelar la población con la línea continua en la Figura 9 (b) es en el mejor de los casos una aproximación de la realidad. Sin embargo, los matemáticos frecuentemente modelarán una situación discreta con un modelo continuo. Mientras seamos conscientes de sus limitaciones, aún podemos usar el modelo para hacer predicciones razonables. Por ejemplo, podríamos decir que quedan aproximadamente 7 conejos en la conejera después de 7 horas.
Vimos la ventaja de usar la notación de funciones al final de nuestro modelo anterior, así que empleemos la notación de funciones un poco antes en este modelo. Vamos a dejar
\[N(t)=\text { the number of rabbits remaining after } t \text { hours. }\]
Inicialmente, en el tiempo t = 0, hay 25 conejos en la conejera. Así, escribimos
\[N(0)=25\]
Podría ser más fácil pensar en perder 5 conejos cada 2 horas como equivalente a perder “en promedio” 2.5 conejos cada hora. Así, al final de 1 hora, el número de conejos disminuye en un incremento de 2.5 conejos, y escribimos
\[N(1)=25-2.5(1)\]
Al cabo de 2 horas, la población de conejos disminuye en 2 incrementos de 2.5 conejos y podemos escribir
\[N(2)=25-2.5(2)\]
Al cabo de 3 horas, la población de conejos disminuye en 3 incrementos de 2.5 conejos y podemos escribir
\[N(3)=25-2.5(3)\]
Se desarrolla un patrón claro, particularmente cuando resumimos estos resultados en la Tabla\(\PageIndex{2}\).
| t | N (t) |
|---|---|
| 0 | 25 |
| 1 | 25 − 2.5 (1) |
| 2 | 25 − 2.5 (2) |
| 3 | 25 − 2.5 (3) |
Tabla\(\PageIndex{2}\) Determinar una ecuación modelo.
La tabla\(\PageIndex{2}\) revela una relación entre el número de conejos N y el tiempo t que se puede describir mediante la ecuación\[N(t)=25-2.5 t\]
\[N(t)=25-2.5 t\]
El lector cuidadoso volverá a comprobar que la ecuación (4) devuelve el número correcto de conejos a los tiempos t = 0, 1, 2 y 3, como se registra en la Tabla\(\PageIndex{2}\).
Hay dos observaciones importantes que podemos hacer sobre la ecuación (4).
- El 25 in\(N(t) = 25 − 2.5t\) es la población inicial de conejos y corresponde al punto (0, 25) de la Figura\(\PageIndex{8}\) (a).
- El −2.5 in\(N(t) = 25−2.5t\) es la tasa a la que la población de conejos está disminuyendo “en promedio” (2.5 conejos por hora).
La ecuación (4) se puede utilizar para predecir el número de conejos que quedan en la conejera después de t = 7 horas. Simplemente sustituya t = 7 en la ecuación (4).
\[N(7)=25-2.5(7)=7.5\]
Es importante señalar que la predicción realizada por la ecuación del modelo es idéntica a la realizada por la gráfica modelo en la Figura\(\PageIndex{9}\) (b).
No obstante, nuevamente señalar que esta ecuación es un modelo continuo, y su predicción de que 7.5 conejos permanecen en la conejera no es realista (a menos que ese zorro se soltara de nuevo). Sin embargo, si somos conscientes de las deficiencias del modelo, la ecuación aún puede ser utilizada como una buena herramienta predictiva. Por ejemplo, podríamos volver a decir que aproximadamente 7 conejos permanecen en la conejera después de 7 horas. Esto se puede escribir\(N(7) \approx 7\), lo que significa que “después de 7 horas, quedan aproximadamente 7 conejos en la conejera”.
Determinar el modelo de ecuaciones a partir de la gráfica
La señora Burke pone un detector de movimiento en la parte delantera de su salón de clases, luego coloca a uno de sus alumnos a una distancia fija del detector y le pide que se acerque al detector a una velocidad constante. El detector mide la distancia d (en metros) del alumno desde el detector en función del tiempo t (en segundos). La gráfica de distancia d versus tiempo t se da en la Figura\(\PageIndex{10}\).
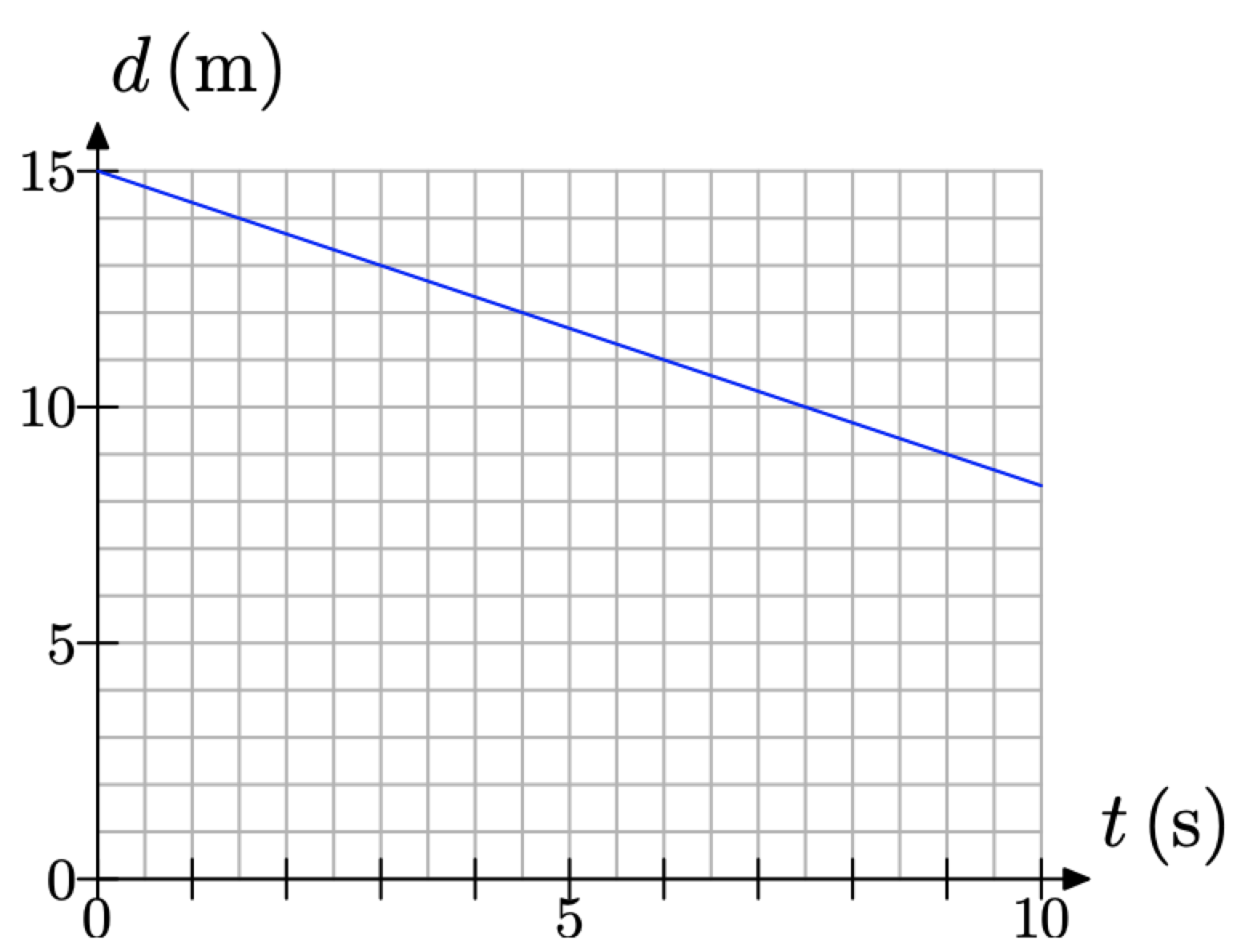
Figura\(\PageIndex{10}\). El detector mide la distancia entre el alumno y el detector versus el tiempo.
Es una cuestión sencilla determinar la distancia inicial del alumno con respecto al detector. Solo necesitamos determinar el valor de d en el tiempo t = 0 segundos. El resultado se ubica en el punto (0, 15), como se muestra en la Figura\(\PageIndex{11}\) (a). Así, el alumno se instala a una distancia inicial de 15 metros del detector.
Para determinar la velocidad a la que el estudiante se acerca al detector, necesitamos hacer un poco más de trabajo. Examine la gráfica y elija dos puntos en la línea. Hace las cosas un poco más fáciles si eliges puntos en la línea que están situados en la intersección de dos líneas de cuadrícula, pero como mostraremos, esto no es necesario. Con este pensamiento en mente, hemos escogido los puntos P (3, 13) y Q (6, 11) en la línea, como se muestra en la Figura\(\PageIndex{11}\) (b).
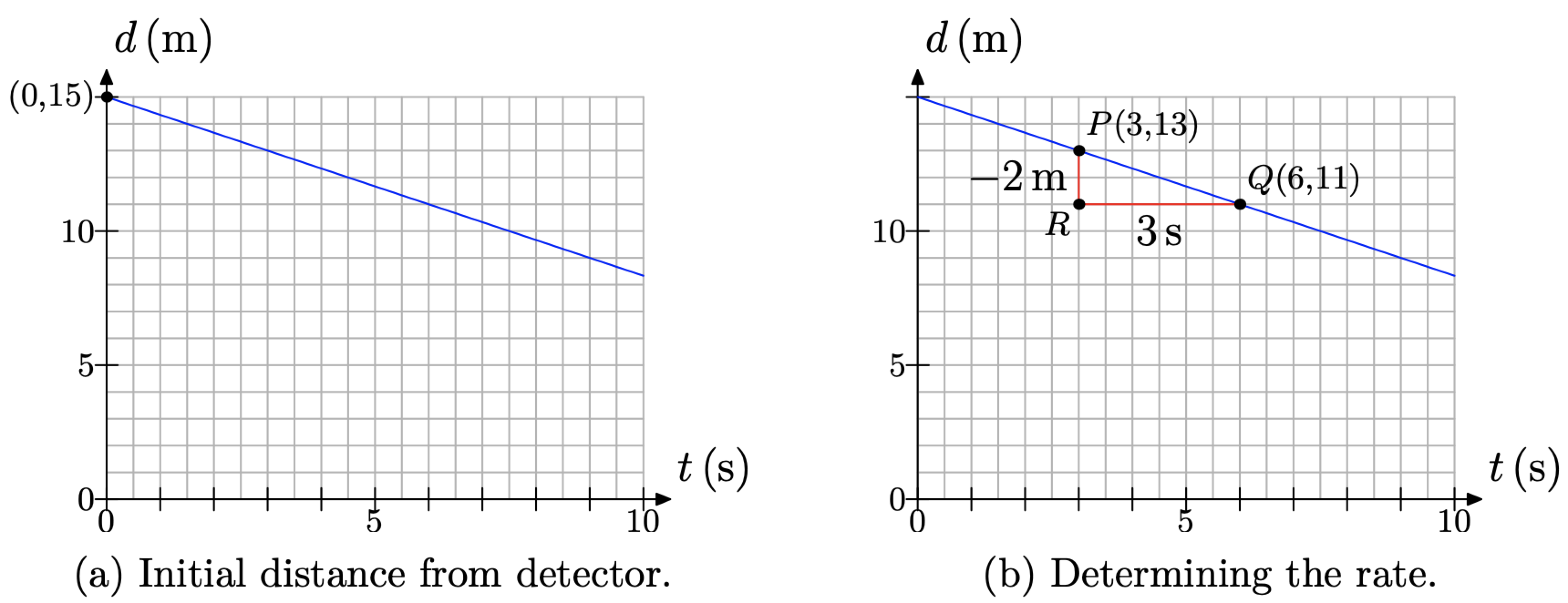
Figura\(\PageIndex{11}\). Determinar la distancia inicial y la tasa.
Dibuja un triángulo rectángulo\(\triangle P Q R\) con lados paralelos a los ejes, como se muestra en la Figura\(\PageIndex{11}\) (b). Determinar la longitud de cada lado del triángulo rectángulo.
- La PR lateral tiene 2 cajas de longitud, pero cada caja representa 1 metro, por lo que el lado P R representa una disminución de 2 metros de distancia del detector. Es por eso que hemos usado el signo menos al etiquetar la PR lateral con −2m en la Figura\(\PageIndex{11}\) (b).
- El RQ lateral es de 6 cajas de longitud, pero 2 cajas representa 1 segundo, por lo que el RQ lateral representa un incremento de 3 segundos en el tiempo. Es por ello que hemos etiquetado RQ lateral con 3 s en la Figura\(\PageIndex{11}\) (b).
Así, la distancia entre el alumno y el detector está disminuyendo a una velocidad de 2 metros cada 3 segundos.
¿Qué pasaría si escogiéramos dos puntos diferentes en la línea? Consideremos el caso en la Figura\(\PageIndex{12}\), donde hemos escogido los puntos de la línea en P (3, 13) y Q (9, 9). También hemos decidido dibujar el triángulo rectángulo\(\triangle P Q R\) en el lado opuesto de la línea. No obstante, tenga en cuenta nuevamente que los lados del triángulo rectángulo\(\triangle P Q R\) son paralelos a los ejes horizontal y vertical.
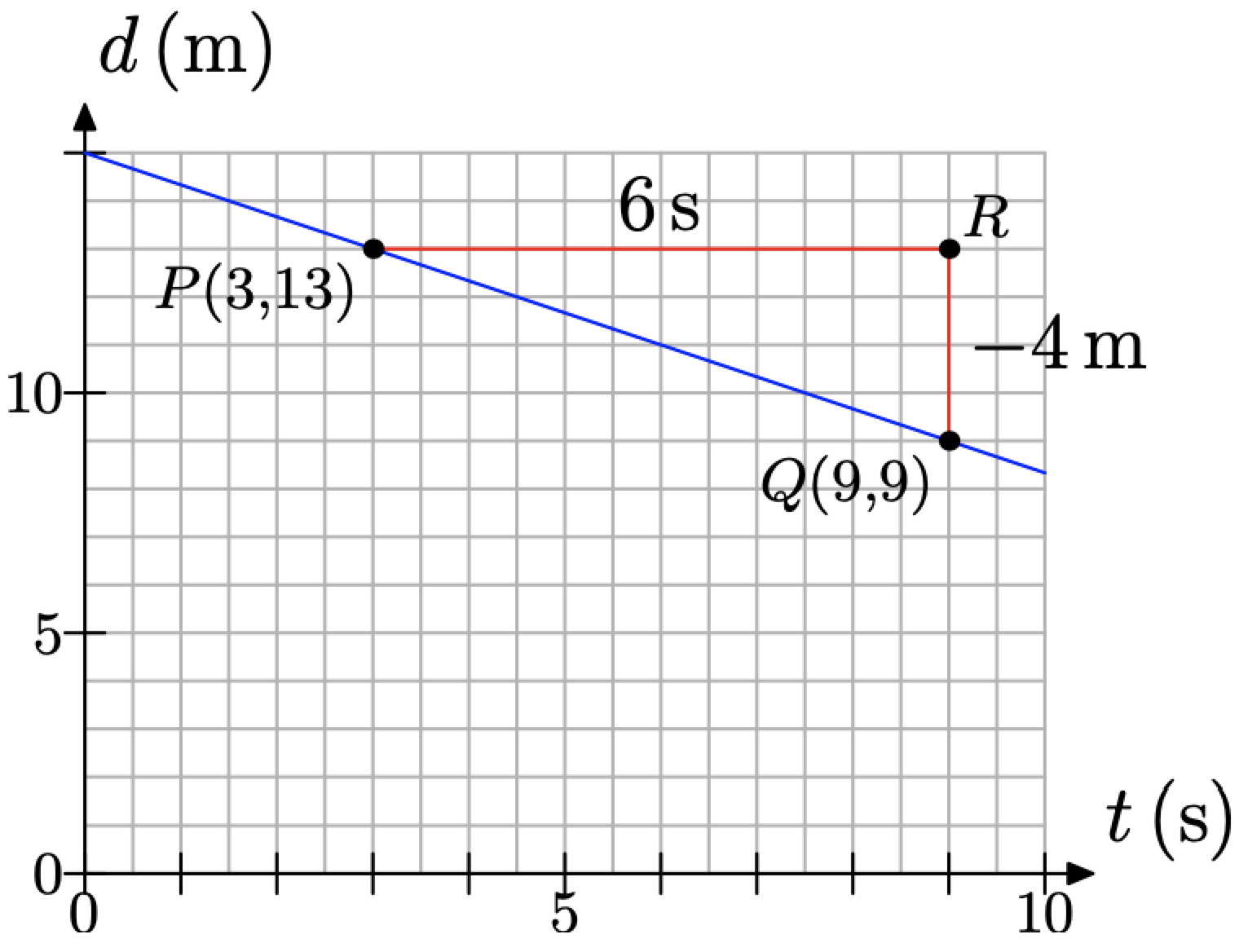
Figura\(\PageIndex{12}\). Determinar la tasa.
Determinar la longitud de cada lado del triángulo\(\triangle P Q R\).
- La PR lateral tiene 12 cajas de longitud, pero 2 cajas representan 1 segundo, por lo que la PR lateral representa un incremento de 6 segundos en el tiempo. Es por ello que hemos etiquetado el lado P R con 6 s en la Figura\(\PageIndex{12}\).
- El RQ lateral es de 4 cajas de longitud, pero cada caja representa 1 metro, por lo que el lado RQ representa una disminución de 4 metros de distancia del detector. Es por eso que hemos utilizado un signo menos al etiquetar el lado RQ con −4 m en la Figura\(\PageIndex{12}\).
Así, la distancia entre el alumno y el detector está disminuyendo a una velocidad de 4 metros cada 6 segundos. En símbolos, escribiríamos que la tasa es
\[\text { Rate }=\frac{-4 \mathrm{m}}{6 \mathrm{s}}=-\frac{4}{6} \mathrm{m} / \mathrm{s}\]
Obsérvese, sin embargo,\[\text { Rate }=-\frac{2}{3} \mathrm{m} / \mathrm{s}\] que esto reduce a lo que es idéntico a la tasa encontrada anteriormente al usar los puntos P y Q de la Figura\(\PageIndex{11}\) (b).
El hecho de que estas tasas sean equivalentes se debe a que los triángulos (\ triángulo P Q R\) en la Figura\(\PageIndex{11}\) (b) y Figura\(\PageIndex{12}\) son triángulos similares, por lo que sus lados son proporcionales. Por lo tanto, no importa qué dos puntos escojas en la línea, ni importa de qué lado de la línea coloques tu triángulo rectángulo. Así, el único requisito es que dibujes un triángulo rectángulo con lados paralelos a los ejes de coordenadas.
Por último, veamos si podemos desarrollar una ecuación modelo. Vamos a definir\[d(t)=\text { the distance from the detector at time } t\]
Inicialmente, el alumno se encuentra a 15 metros del detector. Es decir, en el tiempo t = 0, la distancia desde el detector es de 15 metros. En símbolos, escribimos
\[d(0)=15\]
La distancia disminuye a una velocidad de 2 metros cada 3 segundos. Esto equivale a decir que la distancia disminuye 2/3 metros cada segundo. Al final de 1 segundo, la distancia ha disminuido en 1 incremento de 2/3 metros, por lo que la distancia desde el detector viene dada por
\[d(1)=15-\frac{2}{3}(1)\]
Al cabo de 2 segundos, la distancia ha disminuido en 2 incrementos de 2/3 metros, por lo que la distancia desde el detector viene dada por
\[d(2)=15-\frac{2}{3}(2)\]
Al cabo de 3 segundos, la distancia ha disminuido en 3 incrementos de 2/3 metros, por lo que la distancia desde el detector viene dada por
\[d(3)=15-\frac{2}{3}(3)\]
Surge un patrón claro, particularmente si se resumen los resultados como lo tenemos en la Tabla\(\PageIndex{3}\).
| t | d (t) |
|---|---|
| 0 | 15 |
| 1 | 15 − (2/3) (1) |
| 2 | 15 − (2/3) (2) |
| 3 | 15 − (2/3) (3) |
Tabla\(\PageIndex{3}\) Determinar una ecuación modelo.
La tabla\(\PageIndex{3}\) revela que la relación lineal (ver Figura\(\PageIndex{10}\)) entre la distancia d del detector en el tiempo t puede ser modelada por la ecuación\[d(t)=15-\frac{2}{3} t\]
Nuevamente, el lector cuidadoso comprobará que la ecuación (5) devuelve la distancia correcta d en los tiempos t = 0, 1, 2 y 3 registrados en la Tabla\(\PageIndex{3}\).
Hay que hacer dos observaciones importantes sobre la ecuación (5).
1. El 15 en d (t) = 15− (2/3) t es la distancia inicial del detector y corresponde al punto (0, 15) de la Figura\(\PageIndex{11}\) (a).
2. El −2/3 en d (t) = 15− (2/3) t es la velocidad a la que cambia la distancia entre el alumno y el detector según se determina en la Figura\(\PageIndex{11}\) (b). Es negativo porque la distancia va disminuyendo con el tiempo.
La ecuación (5) se puede utilizar para hacer predicciones. Por ejemplo, para determinar la distancia entre el alumno y el detector al final de 9 segundos, inserte t = 9 en la ecuación (5).
\[d(9)=15-\frac{2}{3}(9)=15-6=9\]
Por supuesto, la notación d (9) = 9 se interpreta en el sentido de que “la distancia entre el alumno y el detector después de 9 segundos es de 9 metros.


