3.2: Pendiente

En la sección anterior sobre Modelos Lineales, vimos que si la variable dependiente estaba cambiando a una tasa constante con respecto a la variable independiente, entonces la gráfica era una línea. Si la tasa era positiva, entonces a medida que barrimos los ojos de izquierda a derecha, la línea subió hacia arriba, la variable dependiente se incrementó con cambios crecientes en la variable independiente. Si la tasa fue negativa, entonces la gráfica cayó a la baja, disminuyendo la variable dependiente con cambios crecientes en la variable independiente. También puede haber aprendido que tasas más altas llevaron a líneas más pronunciadas (líneas que subieron más rápidamente) y tasas más bajas llevaron a líneas que eran menos empinadas.

En esta sección, conectaremos el concepto intuitivo de tasa desarrollado en el apartado anterior con una definición formal de la pendiente de una línea. Para comenzar, indiquemos de frente lo que se entiende por la pendiente de una línea.

Definición

La pendiente es un número que nos dice qué tan rápido sube o baja una línea.

Si la pendiente es un número que está directamente conectado a la “pendiente” de una línea, entonces deberíamos tener ciertas expectativas.

Expectativas

1. Las líneas con pendiente positiva deben inclinarse cuesta arriba (ya que nuestros ojos barren de izquierda a derecha).
2. Las líneas con pendiente negativa deben inclinarse cuesta abajo (ya que nuestros ojos barren de izquierda a derecha).
3. Debido a que cualquier línea horizontal no se incline ni cuesta arriba ni cuesta abajo, esperamos que tenga pendiente igual a cero.
4. Las líneas con una pendiente positiva más grande deben subir más rápidamente que las líneas con una pendiente positiva más pequeña.
5. Si dos líneas tienen pendiente negativa, entonces la línea que tiene la pendiente con mayor valor absoluto debería caer más rápidamente que la otra línea.

Queda por definir cómo calcular la pendiente de una línea en particular. Cualquiera que sea la definición que escojamos, debe ajustarse a las expectativas señaladas anteriormente. También nos gustaría que la definición de pendiente se ajuste al concepto de tasa desarrollado en el apartado anterior. Así, hacemos la siguiente definición.

Definición: Pendiente

La pendiente de una línea es la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente.

Observe cómo se usa la palabra “cambio” Definición. Es importante entender que el cambio en alguna cantidad puede ser positivo, negativo o cero. Por ejemplo, si la temperatura exterior es\(40^{\circ} \mathrm{F}\) cuando salgo de mi casa a las 6 AM, y al mediodía la temperatura es de 65◦ F, entonces el cambio de temperatura es positivo\(25^{\circ} \mathrm{F}\). Por otro lado, si la temperatura exterior es\(65^{\circ} \mathrm{F}\) al mediodía, y la temperatura es\(50^{\circ} \mathrm{F}\) cuando regreso a casa por la noche, entonces el cambio de temperatura es negativo de 15 grados Fahrenheit.

Al calcular el cambio en una cantidad, siga esta regla.

Definición: Cambio en la cantidad

Cambio en la Cantidad = Última Medición − Medición Antigua.

Así, si T representa la temperatura y\(\Delta T\) representa el cambio en la temperatura, entonces en nuestro primer caso (tomando la temperatura por la mañana y luego más tarde al mediodía), el cambio de temperatura es\[\Delta T=\text { Latter }-\text { Former }=65^{\circ} \mathrm{F}-40^{\circ} \mathrm{F}=25^{\circ} \mathrm{F}\]

Este resultado positivo representa un aumento en la temperatura de\(25^{\circ} \mathrm{F}\).

En el segundo caso (tomando la temperatura al mediodía y luego más tarde en la noche), el cambio de temperatura es

\[\begin{align*} \Delta T &= \text{Latter} - \text{Former} \\[4pt] &=50^{\circ} \mathrm{F}-65^{\circ} \mathrm{F} \\[4pt] &=-15^{\circ} \mathrm{F} \end{align*}\]

Este resultado negativo representa una disminución en la temperatura de\(15^{\circ} \mathrm{F}\)

Consejo 3

Los lectores deben señalar que la dirección de la resta es sumamente importante. Para detectar el cambio en una cantidad, restar siempre la primera medición (anterior) de la segunda (posterior) medición.

Ejemplo\(\PageIndex{1}\)

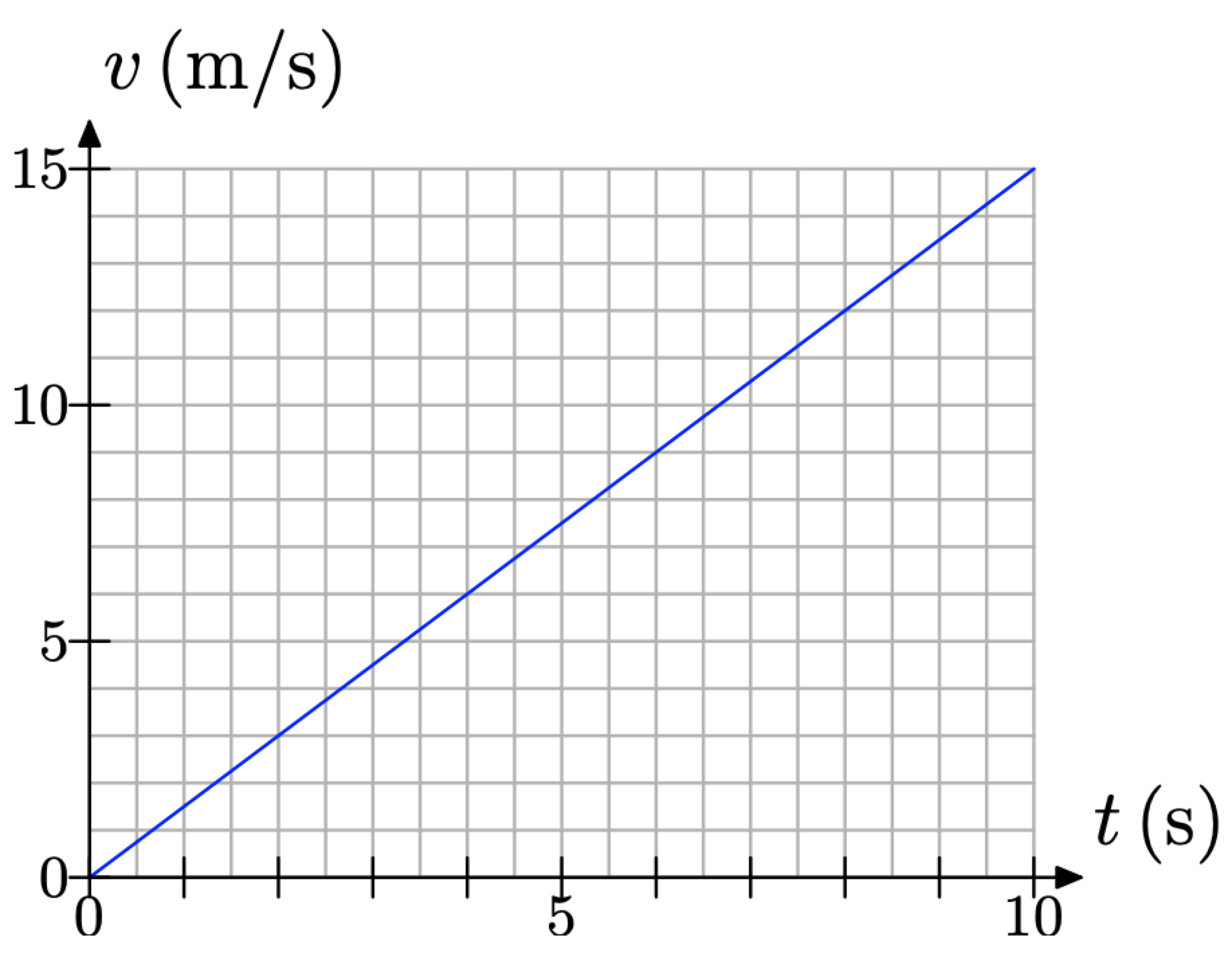
Una pelota se alza en reposo en la parte superior de una rampa larga. Se le da un pequeño toque y comienza a rodar por la rampa. Se grafica la velocidad v de la bola (en metros por segundo) versus el tiempo t (en segundos) en la Figura\(\PageIndex{1}\).

Determinar la pendiente de la línea.

Solución

Hemos definido la pendiente como la velocidad a la que la variable dependiente está cambiando con respecto a la variable independiente. En este caso, la velocidad v de la pelota “depende” de la cantidad de tiempo t que haya transcurrido. En consecuencia, v es la variable dependiente y se ha colocado sobre el eje vertical.3 Por otro lado, t es la variable independiente y se le ha asignado el eje horizontal.

Figura\(\PageIndex{1}\). Velocidad versus tiempo.

Para determinar la velocidad a la que v está cambiando con respecto a t (la pendiente de la línea), primero seleccionamos dos puntos P (2, 3) y Q (8, 12) en la línea, como se muestra en la Figura\(\PageIndex{2}\). Al barrer los ojos de izquierda a derecha (una convención que siempre seguiremos cuando se trata de pendiente), el punto P ocurre antes del punto Q. Por lo tanto, consideramos P la medida “anterior” y el punto Q la “última” medida.

Figura\(\PageIndex{2}\). Determinar la pendiente de la línea.

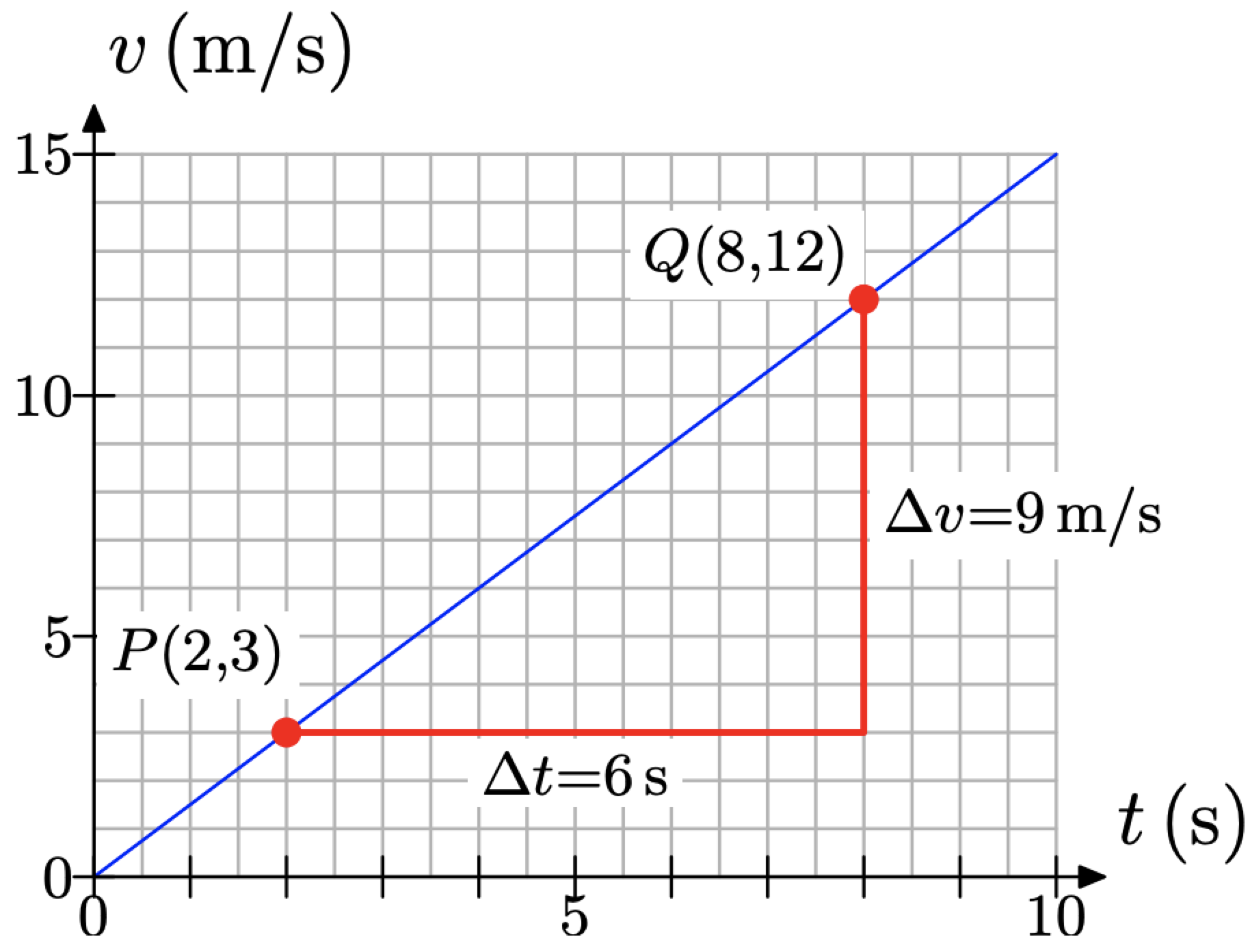
En el punto P, el tiempo es t = 2 segundos, luego en el punto Q el tiempo es t = 8 segundos. El cambio en t se encuentra restando la primera medida de la segunda.

\[\Delta t=8 s-2 s=6 s \nonumber\]

En el punto P, la velocidad es v = 3 metros por segundo, luego en el punto Q la velocidad es v = 12 metros por segundo. De ahí que el cambio en v sea

\[\Delta v=12 \mathrm{m} / \mathrm{s}-3 \mathrm{m} / \mathrm{s}=9 \mathrm{m} / \mathrm{s} \nonumber\]

Finalmente, la pendiente de la línea se define como la velocidad a la que la variable dependiente v está cambiando con respecto a la variable independiente t, es decir,

\[\text { Slope }=\frac{\Delta v}{\Delta t}=\frac{9 \mathrm{m} / \mathrm{s}}{6 \mathrm{s}}=\frac{3 \mathrm{m} / \mathrm{s}}{\mathrm{s}} \nonumber\]

Los científicos prefieren escribir esto como 1.5\(\mathrm{m} / \mathrm{s}^{2}\), pero esto podría no ser tan intuitivo como escribir 1.5 (m/s) /s, lo que indica que la velocidad está aumentando a una velocidad de 1.5 m/s cada segundo. Esto tiene mucho sentido ya que una bola rodando por una rampa cobrará velocidad con el paso del tiempo. La pendiente proporciona una descripción numérica exacta de cómo aumenta la velocidad con respecto al tiempo.

Tenga en cuenta que nuestra definición de la pendiente de la línea satisface uno de nuestros objetivos: la pendiente es precisamente la misma que la noción de tasa descrita en el apartado anterior. Efectivamente, anote el triángulo rectángulo que hemos dibujado en la Figura\(\PageIndex{2}\). El borde inferior del triángulo tiene 12 cajas de largo, pero cada 2 cajas representa un segundo, por lo que este desplazamiento en la dirección del tiempo t es de 6 segundos. El lado vertical del triángulo rectángulo tiene 9 cajas de altura donde cada caja representa 1 metro por segundo. En consecuencia, este borde vertical del triángulo rectángulo representa un desplazamiento positivo de 9 metros por segundo. Así, cada 6 segundos, se produce un incremento en la velocidad de 9 metros por segundo. De ahí que la pelota esté recogiendo velocidad a razón de 9 metros por segundo cada 6 segundos, o equivalentemente, 1.5 metros por segundo cada segundo.

Nota

En la Figura\(\PageIndex{2}\), la velocidad a la que aumenta la velocidad con respecto al tiempo es equivalente a la pendiente de la línea.

Supongamos que habíamos etiquetado nuestros puntos\(P\left(t_{\text { initial }}, v_{\text { initial }}\right)\) y\(Q\left(t_{\text { final }}, v_{\text { final }}\right)\) como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\). Mediciones iniciales y finales.

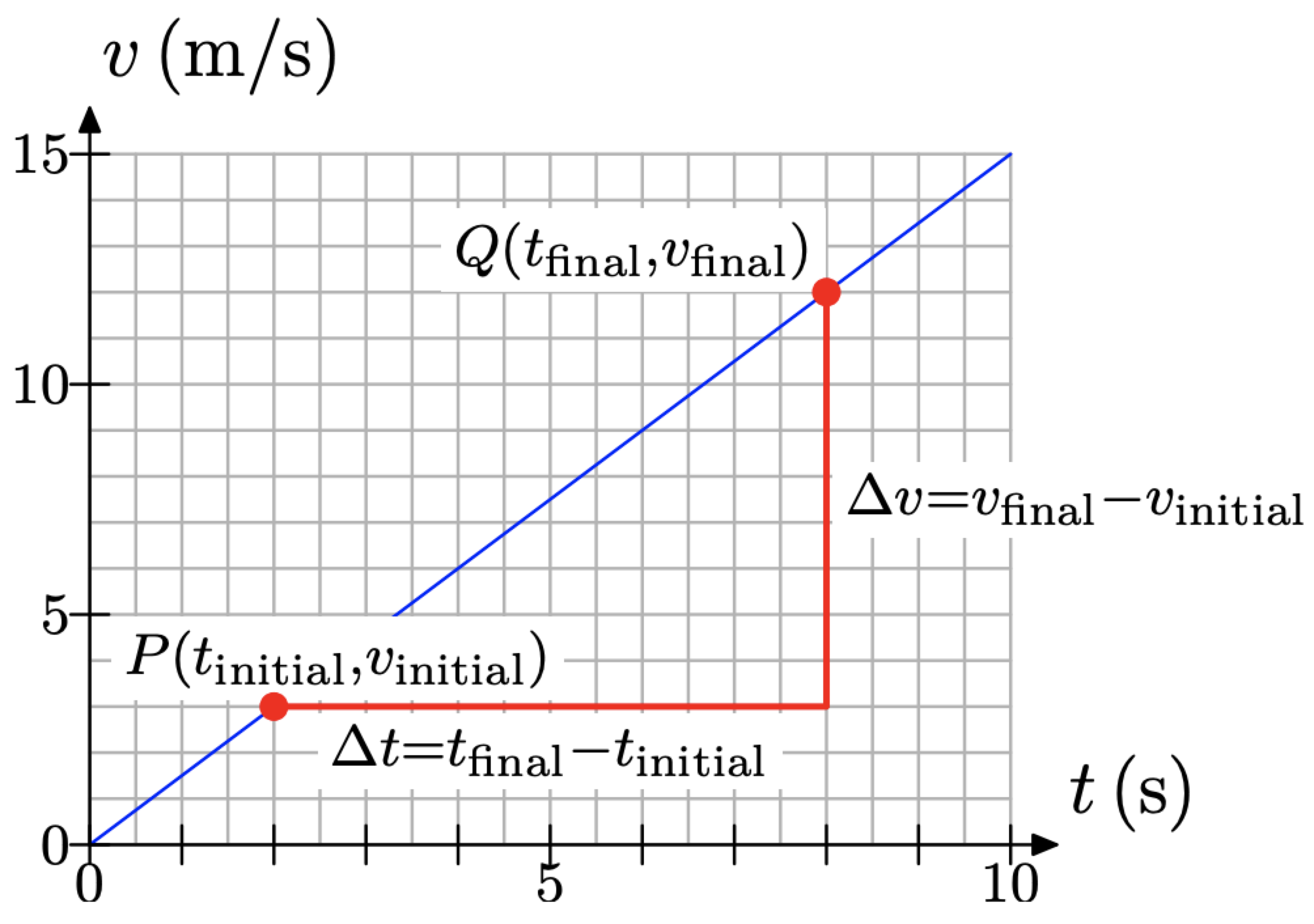
Ahora el cambio en la velocidad v sería

\[\Delta v=v_{\text { final }}-v_{\text { initial }} \nonumber\]

y el cambio en el tiempo t sería

\[\Delta t=t_{\text { final }}-t_{\text { initial }} \nonumber\]

Por lo tanto, la pendiente de la línea se calcularía con la siguiente fórmula.

\[\text { Slope }=\frac{\Delta v}{\Delta t}=\frac{v_{\text { final }}-v_{\text { initial }}}{t_{\text { final }}-t_{\text { initial }}}\nonumber\]

Con\(P\left(t_{\text { initial }}, v_{\text { initial }}\right)=(2 \mathrm{s}, 3 \mathrm{m} / \mathrm{s})\) y\(Q\left(t_{\text { final }}, v_{\text { final }}\right)=(8 \mathrm{s}, 12 \mathrm{m} / \mathrm{s}),\) esto se convierte

\[\text { Slope }=\frac{12 \mathrm{m} / \mathrm{s}-3 \mathrm{m} / \mathrm{s}}{8 \mathrm{s}-2 \mathrm{s}}=\frac{9 \mathrm{m} / \mathrm{s}}{6 \mathrm{s}}=1.5 \mathrm{m} / \mathrm{s}^{2} \nonumber\]

La fórmula de la pendiente

El último cálculo en Ejemplo nos\(\PageIndex{1}\) permite discutir la pendiente de una línea como un concepto puramente matemático, uno que no está enraizado en una aplicación de soporte como en Ejemplo\(\PageIndex{1}\). Tomemos, por ejemplo, la línea que se muestra en la Figura\(\PageIndex{4}\) que pasa por los puntos\(P(−3, −3)\) y\(Q(2, 1)\).

Figura\(\PageIndex{4}\). Calcular la pendiente de una línea en un sistema de coordenadas XY.

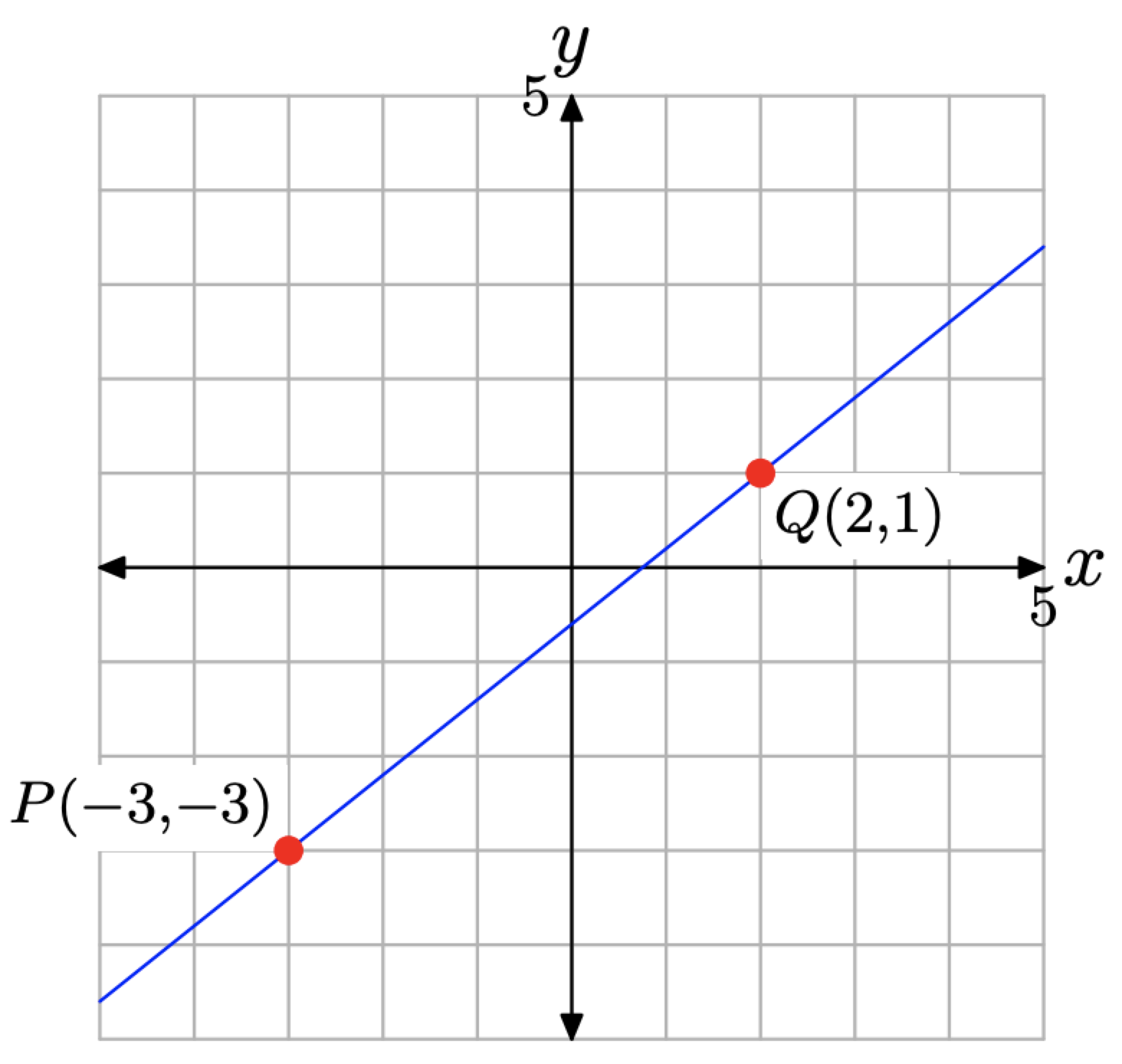
En este ejemplo, la variable dependiente es y y la variable independiente es x, por lo que la pendiente de la línea es\(\Delta y\) (el cambio en y) dividida por\(\Delta x\) (el cambio en x).

\[\text { Slope }=\frac{\Delta y}{\Delta x}\]

Barriendo nuestros ojos de izquierda a derecha, el punto P viene primero, seguido del punto Q. Teniendo en cuenta “último menos ex”, el cambio en y se calcula restando el valor y del punto P del valor y del punto Q. Es decir,

\[\Delta y=1-(-3)=4\]

Del mismo modo, el cambio en x se calcula restando el valor x del punto P del valor x del punto Q. Es decir,

\[\Delta x=2-(-3)=5\]

Así, la pendiente de la línea es

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{4}{5}\]

Alternativamente, podemos usar los puntos P y Q como vértices de un triángulo rectángulo con lados paralelos a los ejes (mostrado en la Figura\(\PageIndex{5}\) (a)). El borde horizontal del triángulo rectángulo es de 5 cajas (cada una representa 1 unidad), por lo que el desplazamiento en x es de 5 unidades. El borde vertical es de 4 cajas (cada una representa 1 unidad), por lo que el desplazamiento en y es de 4 unidades. De ahí que cada vez que x se incremente en 5 unidades, y experimenta un incremento de 4 unidades. Por lo tanto, la pendiente de la línea vuelve a ser 4/5.

Figura\(\PageIndex{5}\). Usando un triángulo rectángulo para determinar la pendiente.

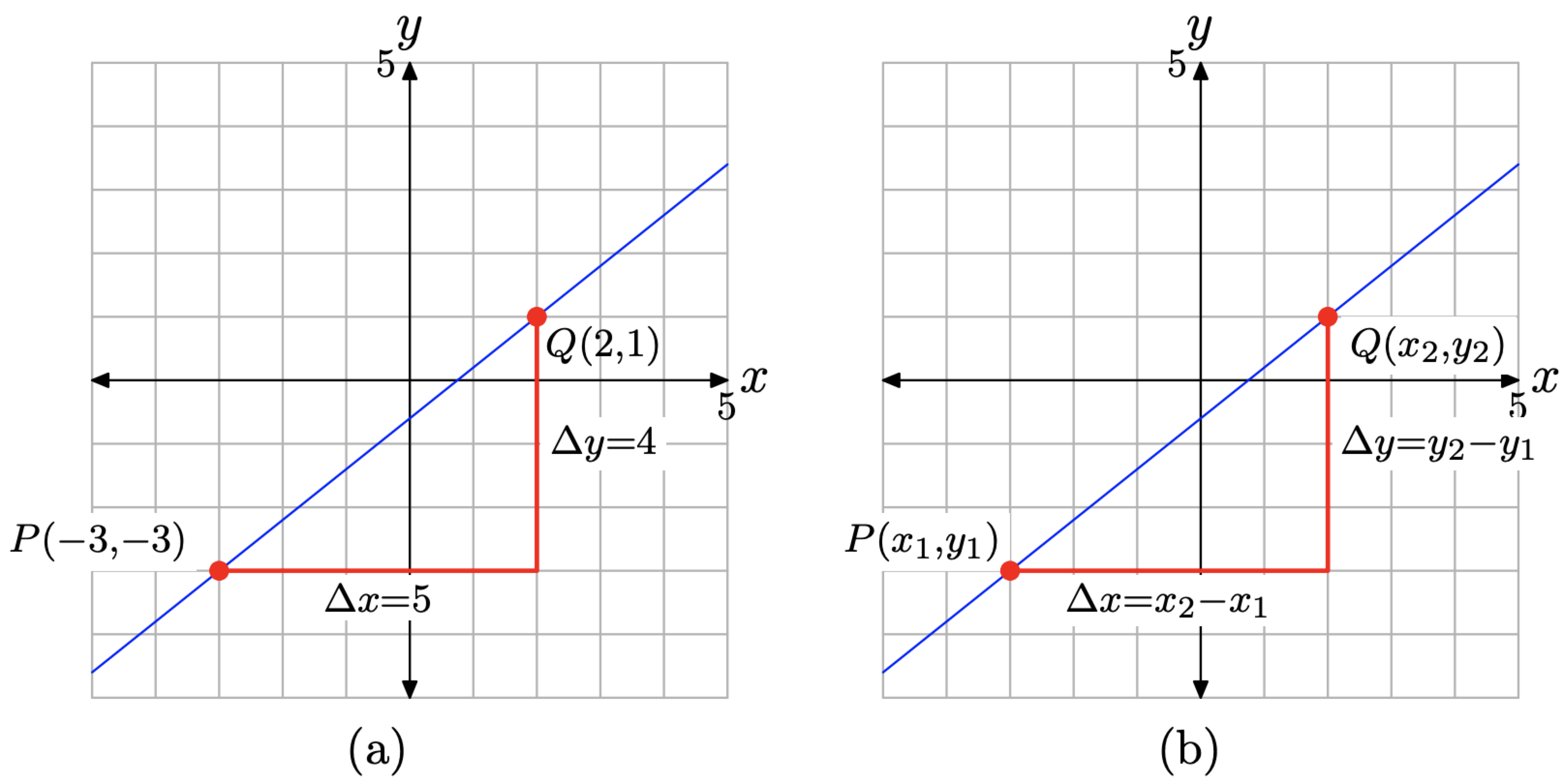
Supongamos que habíamos etiquetado nuestros puntos\(P\left(x_{1}, y_{1}\right)\) y\(Q\left(x_{2}, y_{2}\right)\) como se muestra en la Figura\(\PageIndex{5}\) (b). Ahora el cambio en y sería

\[\Delta y=y_{2}-y_{1}\]

y el cambio en x sería

\[\Delta x=x_{2}-x_{1}\]

Por lo tanto, la pendiente de la línea se calcularía con la siguiente fórmula.

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]

Con\(P\left(x_{1}, y_{1}\right)=(-3,-3)\) y\(Q\left(x_{2}, y_{2}\right)=(2,1),\) esto se convierte

\[\text { Slope }=\frac{1-(-3)}{2-(-3)}=\frac{4}{5}\]

La fórmula de pendiente vale la pena resumir en una definición.

Definición 5

La pendiente de la línea que pasa por los puntos\(P\left(x_{1}, y_{1}\right)\) y\(Q\left(x_{2}, y_{2}\right)\) viene dada por la fórmula

\[\text {Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]

Veamos algunos ejemplos más.

Ejemplo\(\PageIndex{2}\)

Encuentra la pendiente de la línea que pasa por los puntos P (−3, −2) y Q (3, 1).

Solución

Podemos usar la fórmula de pendiente en la Definición 5 para determinar la pendiente. Con\(\left(x_{1}, y_{1}\right)=P(-3,-2)\) y\(\left(x_{2}, y_{2}\right)=Q(3,1)\),

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{1-(-2)}{3-(-3)}=\frac{3}{6}=\frac{1}{2}\]

Los lectores a veces preguntan: “¿Qué punto debería ser\(\left(x_{1}, y_{1}\right)\) y cuál debería ser\(\left(x_{2}, y_{2}\right)\)?” La respuesta corta es: “¡No importa!” Supongamos en cambio, que dejamos\(\left(x_{1}, y_{1}\right)=Q(3,1)\) y\(\left(x_{2}, y_{2}\right)=P(-3,-2)\). Entonces,

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-1}{-3-3}=\frac{-3}{-6}=\frac{1}{2}\]

Debido a que el cambio en cualquier cantidad se encuentra restando la medición anterior de la medición posterior, continuaremos estresando el primer orden. No obstante, si invertimos los puntos como hicimos en nuestro segundo cálculo, tanto el numerador como el denominador invierten signo con este intercambio, así obtenemos la misma respuesta.

Por supuesto, también podemos determinar la pendiente trazando P (−3, −2) y Q (3, 1) y la línea que pasa por P y Q, como hemos hecho en la Figura\(\PageIndex{6}\).

Figura\(\PageIndex{6}\). Determinar la pendiente a partir de la gráfica.

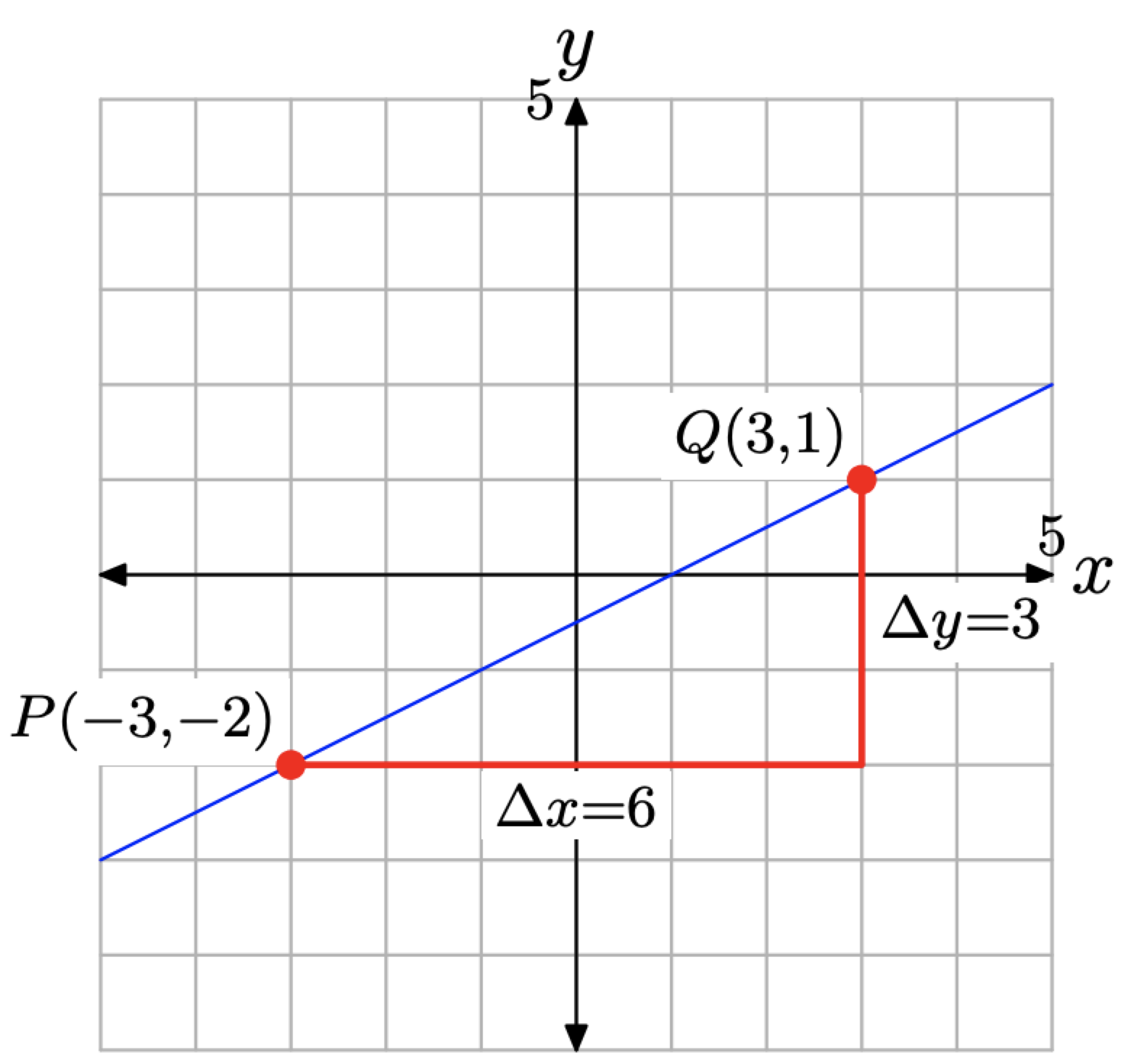
Comenzando en el punto P, para llegar al punto Q, movemos 6 casillas a la derecha, luego 3 casillas hacia arriba, como se muestra en la Figura\(\PageIndex{6}\). De ahí que la pendiente de la línea sea

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{3}{6}=\frac{1}{2}\]

Obsérvese que dos de nuestras expectativas respecto a la pendiente de una línea se cumplen con este ejemplo.

1. La línea a través de P (−3, −2) y Q (3, 1) en la Figura\(\PageIndex{6}\) tiene pendiente 1/2. Este es un número positivo y la línea se incline cuesta arriba (como se esperaba) mientras nos barremos los ojos de izquierda a derecha.
2. La pendiente en este ejemplo es 1/2, que es menor que la pendiente de la línea en la Figura\(\PageIndex{5}\) (a), que fue 4/5. Obsérvese que la línea en la Figura\(\PageIndex{6}\) es menos empinada que la línea de la Figura\(\PageIndex{5}\) (a), que fue otra de nuestras expectativas anteriores respecto a la pendiente de una línea.

Ejemplo\(\PageIndex{3}\)

Encuentra la pendiente de la línea que pasa por los puntos P (−4, 4) y Q (4, −2).

Solución

Podemos usar la fórmula de pendiente en la Definición 5 para determinar la pendiente. Con\(\left(x_{1}, y_{1}\right)=P(-4,4)\) y\(\left(x_{2}, y_{2}\right)=Q(4,-2)\),

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-2-4}{4-(-4)}=\frac{-6}{8}=-\frac{3}{4}\]

También podemos obtener la pendiente de la línea a partir de la gráfica de la Figura\(\PageIndex{7}\). Comenzando en el punto P (−4, 4), mueva 8 unidades hacia la derecha, luego 6 unidades hacia abajo, como se muestra en la Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\). Determinar la pendiente a partir de la gráfica.

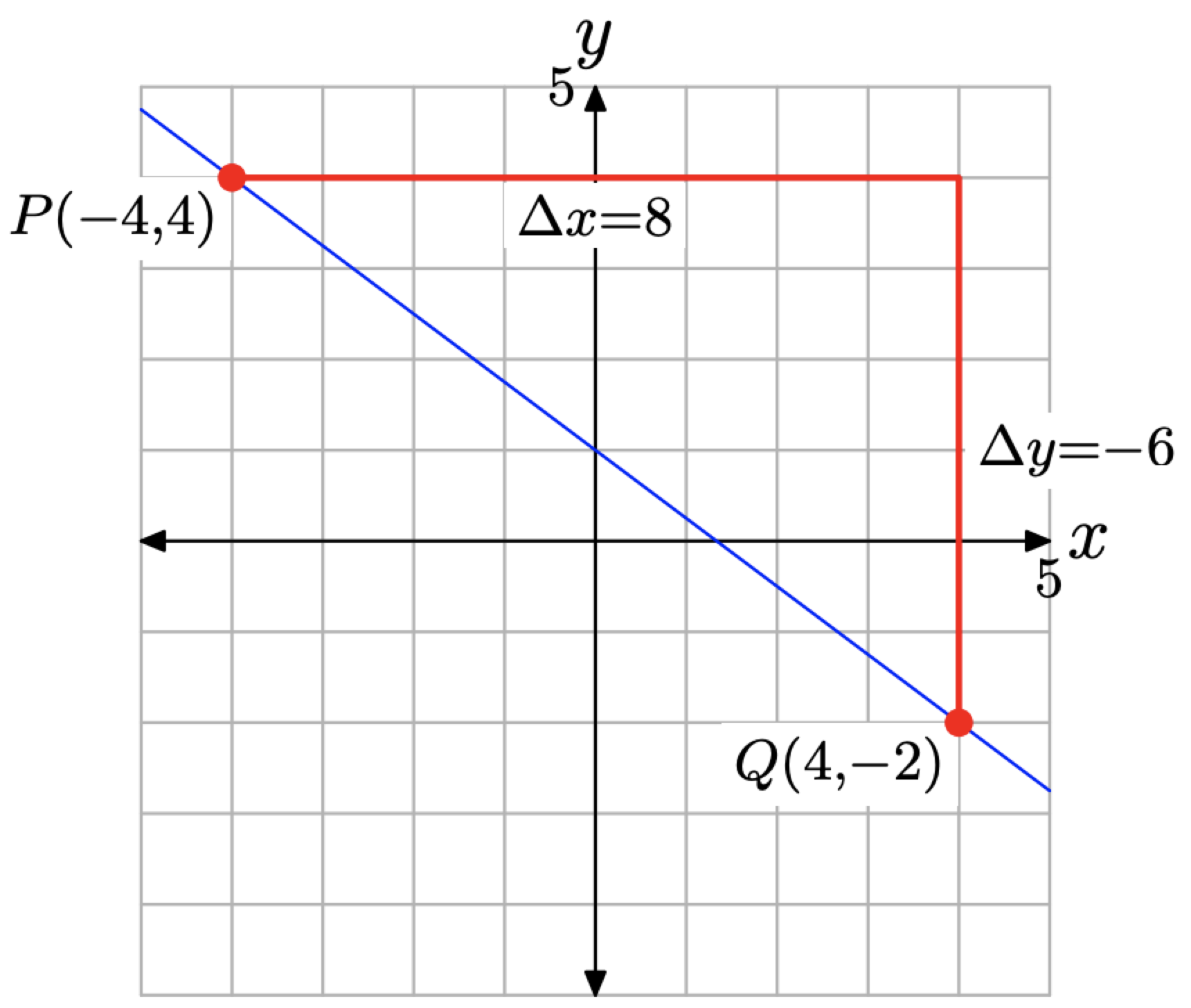
Así, la pendiente de la línea es

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{-6}{8}=-\frac{3}{4}\]

Nuevamente, en este ejemplo se cumple una de nuestras expectativas anteriores respecto a la pendiente de una línea. La pendiente es −3/4, que es un número negativo, y la línea de la Figura se\(\PageIndex{7}\) incline cuesta abajo (a medida que barremos nuestros ojos de izquierda a derecha).

Ejemplo\(\PageIndex{4}\)

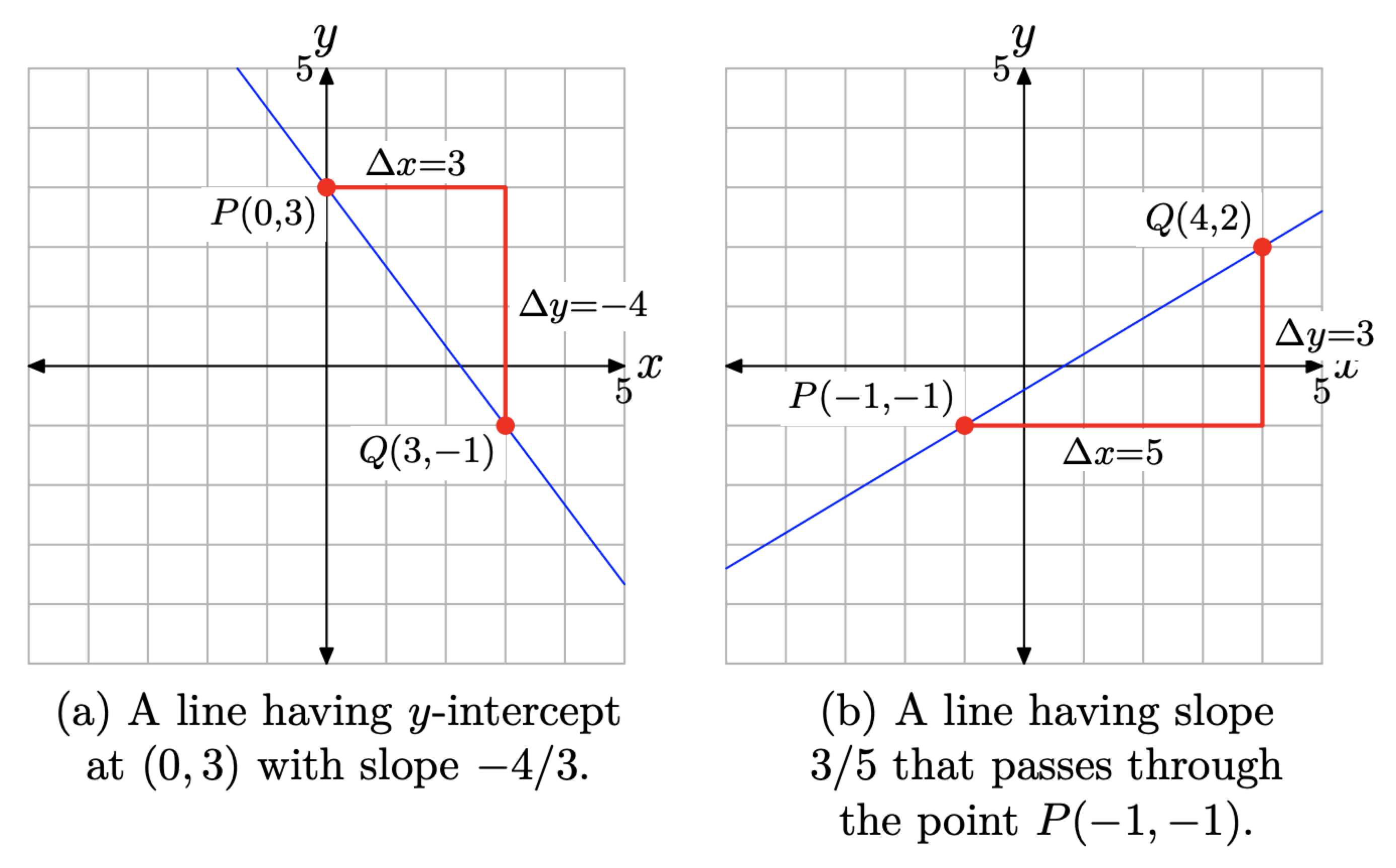
Dibuja una línea que intercepte el eje y en (0, 3) para que la línea tenga pendiente −4/3. Dibuja una segunda línea que pase por el punto P (−1, −1) con pendiente 3/5.

Solución

La pendiente de la primera línea es −4/3. Esto significa que nuestra línea debe inclinarse cuesta abajo (a medida que barremos los ojos de izquierda a derecha). La pendiente es el cambio en y sobre el cambio en x Por lo tanto, cada vez que x aumenta en 3 unidades, y debe disminuir en 4 unidades. Trazar el punto P (0, 3), como se muestra en la Figura\(\PageIndex{8}\) (a). Después, comenzando en P, mueve 3 unidades a la derecha, seguido de 4 unidades hacia abajo hasta el punto Q (3, −1), como se muestra en la Figura\(\PageIndex{8}\) (a). Dibuja la línea requerida, la cual deberá pasar por los puntos P y Q.

Para dibujar la segunda línea, primero grafica el punto P (−1, −1), como se muestra en la Figura\(\PageIndex{8}\) (b). Comenzando en el punto P, mueva 5 unidades hacia la derecha, luego hacia arriba 3 unidades hasta el punto Q (4, 2), como se muestra en la Figura\(\PageIndex{8}\) (b). Dibuja la línea requerida pasando por los puntos P y Q.

Figura\(\PageIndex{8}\)

Líneas paralelas

Debido a que la pendiente controla la “pendiente” de una línea, es sencillo ver que las líneas paralelas deben tener la misma pendiente.

propiedad

Dejar\(\boldsymbol{L}_{1}\) ser una línea que tenga pendiente\(m_{1}\). Dejar\(\boldsymbol{L}_{2}\) ser una línea que tenga pendiente\(m_{2}\). Si\(\boldsymbol{L}_{1}\) y\(\boldsymbol{L}_{2}\) son paralelos, entonces

\[m_{1}=m_{2}\]

Es decir, dos líneas paralelas cualesquiera tienen la misma pendiente.

Ejemplo\(\PageIndex{5}\)

¿Cuál es la pendiente de cualquier línea horizontal? ¿Cuál es la pendiente de cualquier línea vertical?

Solución

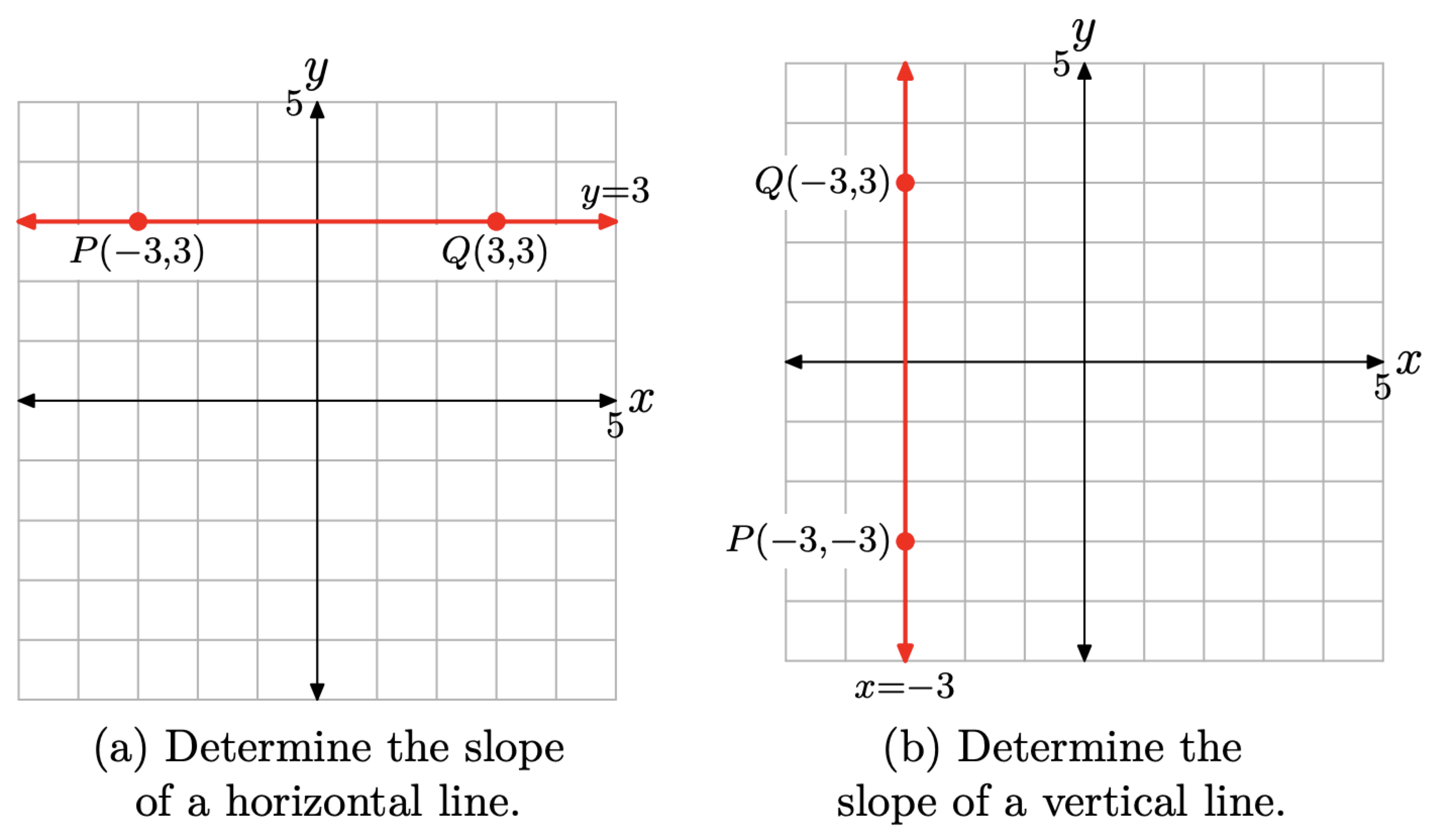
Uno esperaría que nuestra definición verificara que la pendiente de cualquier línea horizontal es cero. Seleccione, por ejemplo, la línea horizontal que se muestra en la Figura 9 (a). Seleccione los puntos (−3, 3) y (3, 3) en esta línea.

Figura\(\PageIndex{9}\)

Con\(\left(x_{1}, y_{1}\right)=(-3,3)\) y\(\left(x_{2}, y_{2}\right)=(3,3)\)

\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-3}{3-(-3)}=\frac{0}{6}=0\]

Así, la línea horizontal en la Figura\(\PageIndex{9}\) (a) tiene pendiente igual a cero, exactamente como se esperaba. Además, todas las líneas horizontales son paralelas a esta línea horizontal y tienen la misma pendiente. Por lo tanto, todas las líneas horizontales tienen pendiente cero.

Supondríamos que la línea vertical en la Figura\(\PageIndex{9}\) (b) tiene pendiente indefinida (exploraremos esto más a fondo en los ejercicios). En la Figura\(\PageIndex{9}\) (b), hemos seleccionado los puntos P (−3, −3) y Q (−3, 3) en la línea vertical. Con\(\left(x_{1}, y_{1}\right)=P(-3,-3)\) y\(\left(x_{2}, y_{2}\right)=Q(-3,-3)\),\[\text { Slope }=\frac{\Delta y}{\Delta x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{3-(-3)}{-3-(-3)}=\frac{6}{0}, \text { which is undefined. }\]

La pendiente de la línea vertical en la Figura\(\PageIndex{9}\) (b) no está definida porque la división por cero no tiene sentido. Además, todas las líneas verticales son paralelas a esta línea vertical y tienen pendiente indefinida.

Ejemplo\(\PageIndex{6}\)

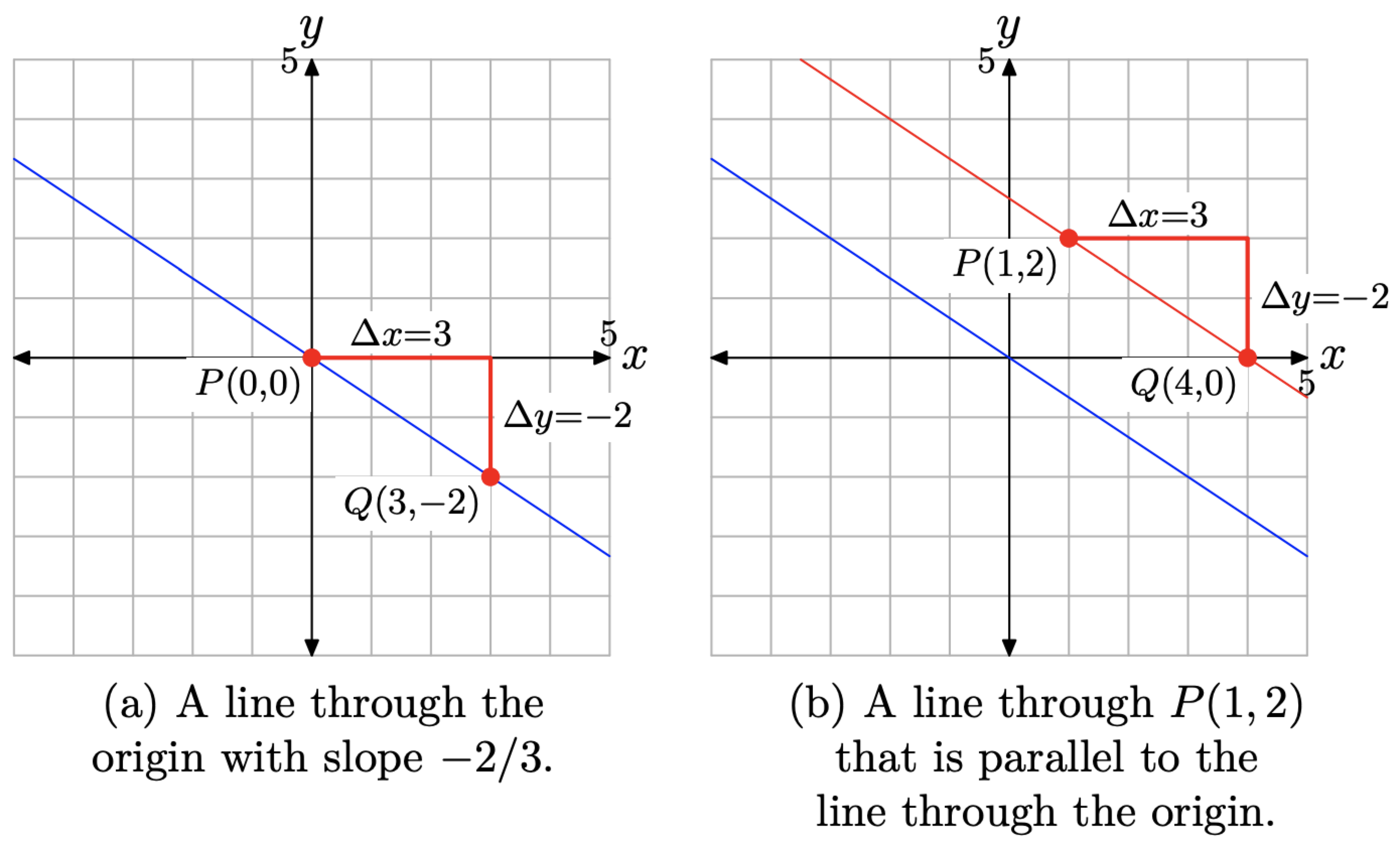
Dibuja una línea a través del punto P (1, 2) que sea paralela a la línea que pasa por el origen con pendiente −2/3.

Solución

Primero dibujaremos una línea a través del origen con pendiente −2/3. Trace el punto P (0, 0), luego mueva 3 unidades a la derecha y 2 unidades hacia abajo hasta el punto Q (3, −2), como se muestra en la Figura\(\PageIndex{10}\) (a). Dibuja una línea a través de los puntos P y Q como se muestra en la Figura\(\PageIndex{10}\) (a).

A continuación, graficar el punto P (1, 2) como se muestra en la Figura\(\PageIndex{10}\) (b). Para trazar una línea a través de este punto que es paralela a la línea a través del origen, esta segunda línea debe tener la misma pendiente que la primera línea. Por lo tanto, comience en el punto P (1, 2), como se muestra en la Figura\(\PageIndex{10}\) (b), luego mueva 3 unidades a la derecha y 2 unidades hacia abajo hasta el punto Q (4, 0). Dibuja una línea a través de los puntos P y Q como se muestra en la Figura\(\PageIndex{10}\) (b). Obsérvese que esta segunda línea es paralela a la primera.

Figura\(\PageIndex{10}\)

Líneas perpendiculares

La relación entre las pendientes de dos líneas perpendiculares no es tan sencilla como la relación entre las pendientes de dos líneas paralelas. Comencemos por señalar los bienes pertinentes.

Propiedad 13

Dejar\(L_{1}\) ser una línea que tenga pendiente\(m_{1}\). Dejar\(L_{2}\) ser una línea que tenga pendiente\(m_{2}\). Si\(L_{1}\) y\(L_{2}\) son perpendiculares, entonces

\[m_{1} m_{2}=-1\]

Es decir, el producto de las pendientes de dos líneas perpendiculares es −1.

Podemos resolver la ecuación (14) para\(m_{1}\) en términos de\(m_{2}\).

\[m_{1}=-\frac{1}{m_{2}}\]

La ecuación (15) nos dice que la pendiente de la primera línea es el recíproco negativo de la pendiente de la segunda línea.

Por ejemplo, supongamos que\(L_{1}\) y\(L_{2}\) son líneas perpendiculares con pendientes\(m_{1}\) y\(m_{2}\), respectivamente

• Si\(m_{2}=2,\) entonces\(m_{1}=-\frac{1}{2}\)
• Si\(m_{2}=\frac{3}{5},\) entonces\(m_{1}=-\frac{5}{3}\)
• Si\(m_{2}=-\frac{2}{3},\) entonces\(m_{1}=\frac{3}{2}\)

Tenga en cuenta que en cada ítem con balas, el producto de las pendientes es −1.

No proporcionaremos una prueba de ecuación (15), pero proporcionaremos alguna evidencia motivadora en forma de gráfica.

Ejemplo\(\PageIndex{7}\)

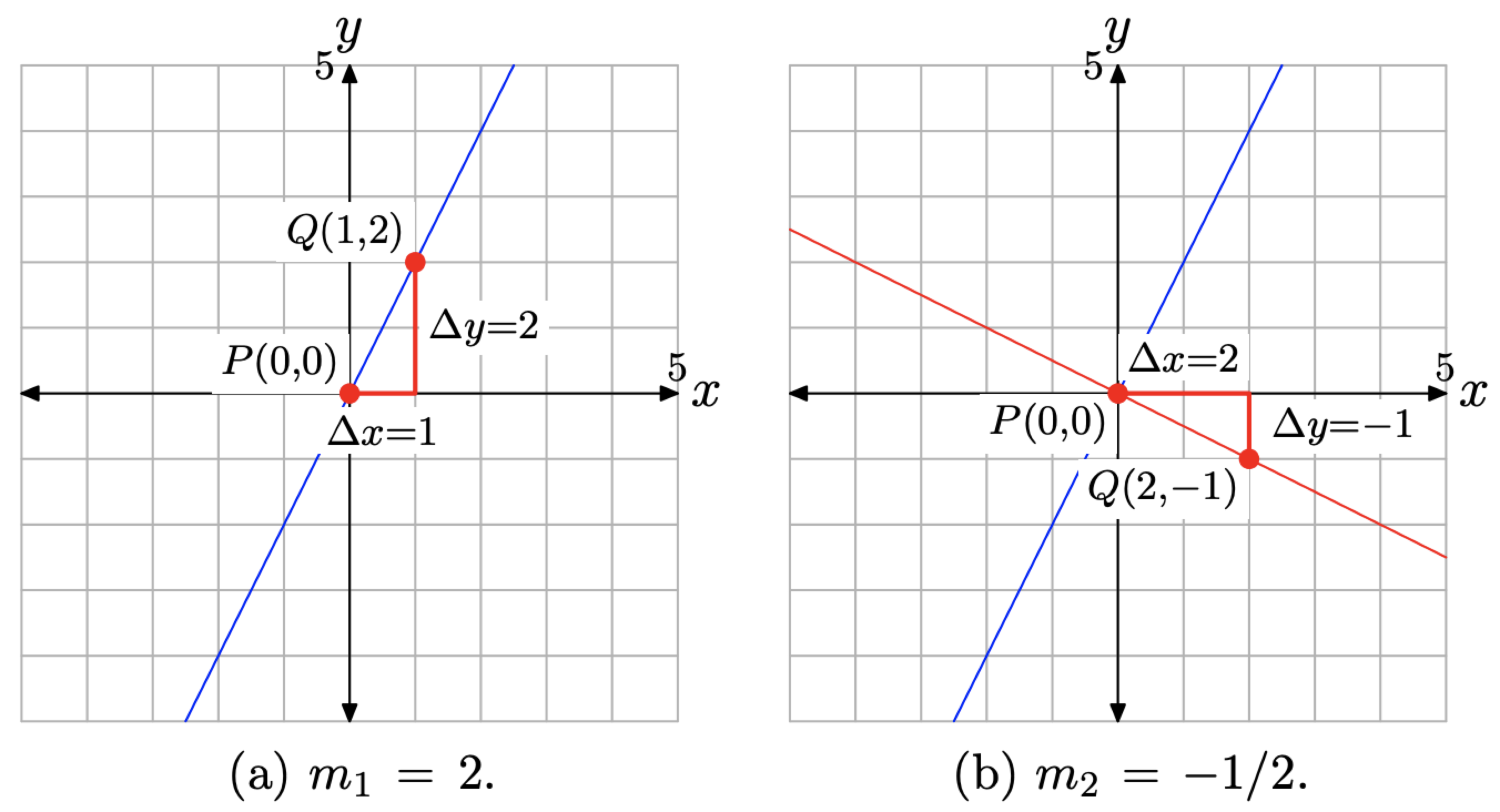
Dibuje las gráficas de las líneas que pasan por el origen teniendo pendientes 2 y −1/2.

Solución

En la Figura\(\PageIndex{11}\) (a), hemos trazado el punto P (0, 0) en el origen, luego movimos 1 unidad a la derecha y 2 unidades hacia arriba hasta el punto Q (1, 2). La línea resultante pasa por el origen y tiene pendiente\(m_{1}=2\) (alternativamente,\(m_{1}=2 / 1\)).

En la Figura\(\PageIndex{11}\) (b), nuevamente hemos trazado el punto P (0, 0) en el origen, luego movimos 2 unidades a la derecha y 1 unidad hacia abajo hasta el punto Q (2, −1). La línea resultante pasa por el origen y tiene pendiente\(m_{2}=-1 / 2\).

Hay dos puntos importantes que hay que hacer sobre las líneas de la Figura\(\PageIndex{11}\) (b).

Las dos líneas de la Figura\(\PageIndex{11}\) (b) son perpendiculares. Se encuentran y forman un ángulo recto de\(90^{\circ}\). Si tiene disponible un prolongador, es posible que desee medir el ángulo entre las dos líneas y tener en cuenta que la medida del ángulo es\(90^{\circ}\).

El producto de las dos pendientes es

\[m_{1} m_{2}=2 \cdot\left(-\frac{1}{2}\right)=-1\]

Figura\(\PageIndex{11}\). Croquizar líneas perpendiculares.