8.4: Función inversa
- Page ID
- 110708
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Como vimos en la última sección, para resolver problemas de aplicación que involucren funciones exponenciales, necesitaremos poder resolver ecuaciones exponenciales como
\(1500 = 1000e^{0.06t}\)o\(300 = 2^x\).
Sin embargo, actualmente no tenemos ninguna herramienta matemática a nuestra disposición para resolver para una variable que aparece como exponente, como en estas ecuaciones. En esta sección, desarrollaremos el concepto de una función inversa, que a su vez se utilizará para definir la herramienta que necesitamos, el logaritmo, en la Sección 8.5.
Funciones uno a uno
Definición\(\PageIndex{1}\)
Se dice que una función dada f es uno a uno si por cada valor y en el rango de f, solo hay un valor x en el dominio de f tal que y = f (x). En otras palabras, f es uno a uno si cada salida y de f corresponde precisamente a una entrada x.
Es más fácil entender esta definición observando diagramas de mapeo y gráficos de algunas funciones de ejemplo.
Ejemplo\(\PageIndex{2}\)
Considere las dos funciones h y k definidas de acuerdo con los diagramas de mapeo en la Figura 1. En la Figura 1 (a), hay dos valores en el dominio que se mapean ambos en 3 en el rango. De ahí que la función h no sea uno-a-uno. Por otro lado, en la Figura 1 (b), para cada salida en el rango de k, solo hay una entrada en el dominio que se mapea sobre él. Por lo tanto, k es una función uno a uno.
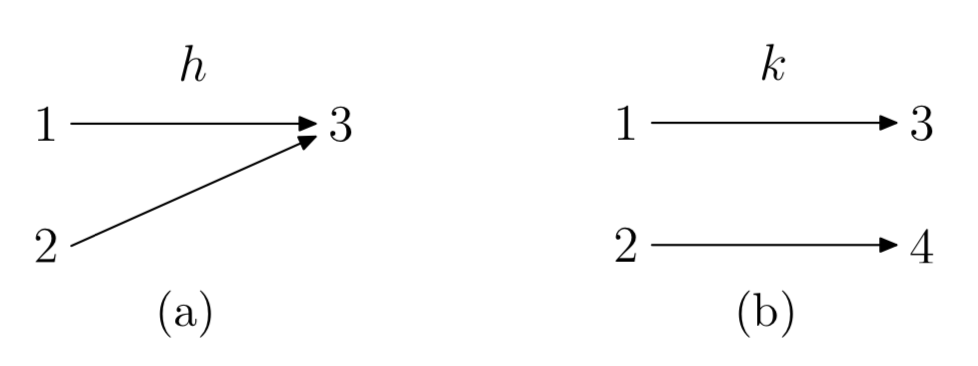
Ejemplo\(\PageIndex{3}\)
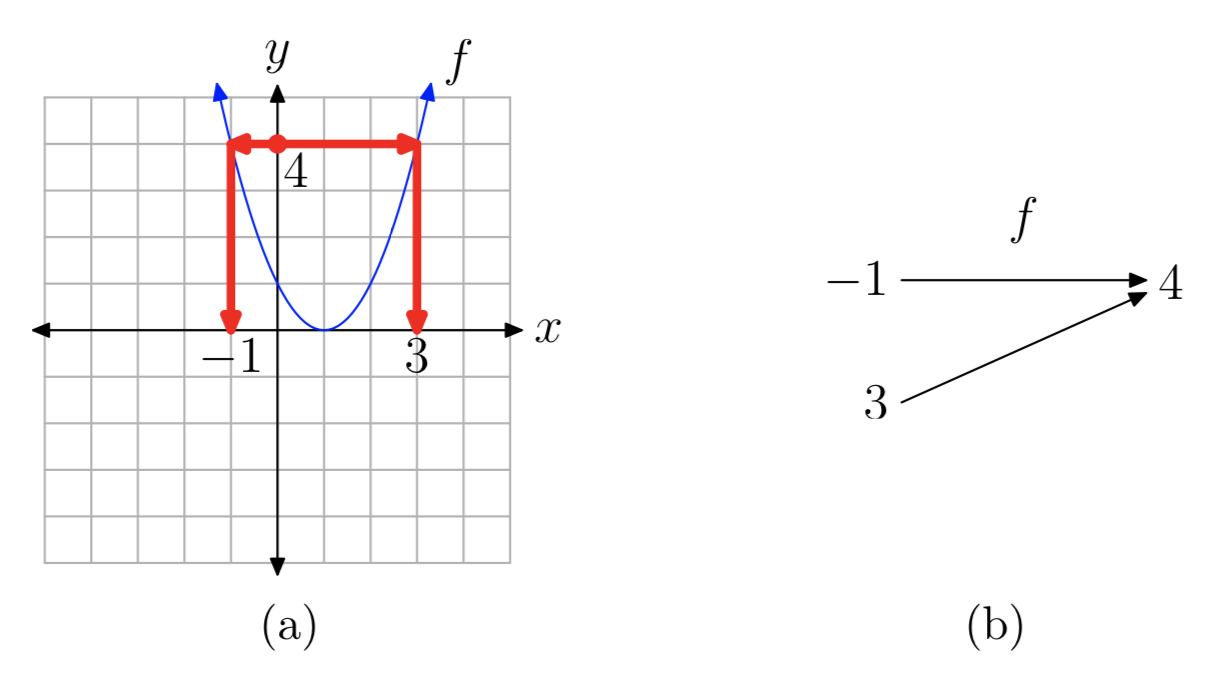
La gráfica de una función se muestra en la Figura 2 (a). Para esta función f, el valor y 4 es la salida correspondiente a dos valores de entrada, x = −1 y x = 3 (ver el diagrama de mapeo correspondiente en la Figura 2 (b)). Por lo tanto, f no es uno a uno.
Gráficamente, esto es evidente dibujando segmentos horizontales desde el punto (0, 4) en el eje y hasta los puntos correspondientes en la gráfica, y luego dibujando segmentos verticales al eje x. Estos segmentos se encuentran con el eje x en − 1 y 3.
Ejercicio\(\PageIndex{4}\)
En la Figura 3, cada valor y en el rango de f corresponde a un solo valor de entrada x Por lo tanto, esta función es uno a uno.
Gráficamente, esto se puede ver dibujando mentalmente un segmento horizontal desde cada punto del eje y hasta el punto correspondiente en la gráfica, y luego dibujando un segmento vertical al eje x. En la Figura 3 se muestran varios ejemplos. Es evidente que este procedimiento siempre dará como resultado un solo punto correspondiente en el eje x, ya que cada valor y solo corresponde a un punto de la gráfica. De hecho, es más fácil solo señalar que dado que cada línea horizontal solo cruza la gráfica una vez, entonces solo puede haber una entrada correspondiente a cada salida.
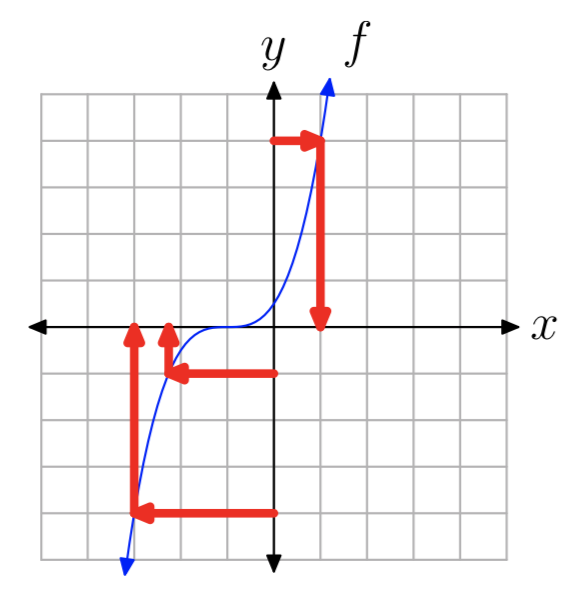
El proceso gráfico descrito en el ejemplo anterior, conocido como prueba de línea horizontal, proporciona un medio visual simple para determinar si una función es uno a uno.
PRUEBA DE LÍNEA
Si cada línea horizontal cruza la gráfica de f como máximo una vez, entonces f es uno a uno. Por otro lado, si alguna línea horizontal cruza la gráfica de f más de una vez, entonces f no es uno-a-uno.
observación 5. De la prueba de línea horizontal se deduce que si f es una función estrictamente creciente, entonces f es uno a uno. Asimismo, cada función estrictamente decreciente es también uno a uno.
Funciones inversas
Si f es uno a uno, entonces podemos definir una función asociada g, llamada la función inversa de f. Vamos a dar una definición formal a continuación, pero la idea básica es que la función inversa g simplemente envía las salidas de f a sus entradas correspondientes. En otras palabras, el diagrama de mapeo para g se obtiene invirtiendo las flechas en el diagrama de mapeo para f.
Ejemplo\(\PageIndex{6}\)
La función f en la Figura 4 (a) mapea 1 a 5 y 2 a −3. Por lo tanto, la función inversa g en la Figura 4 (b) mapea las salidas de f a sus entradas correspondientes: 5 a 1 y −3 a 2. Tenga en cuenta que al invertir las flechas en el diagrama de mapeo para f se obtiene el diagrama de mapeo para g.
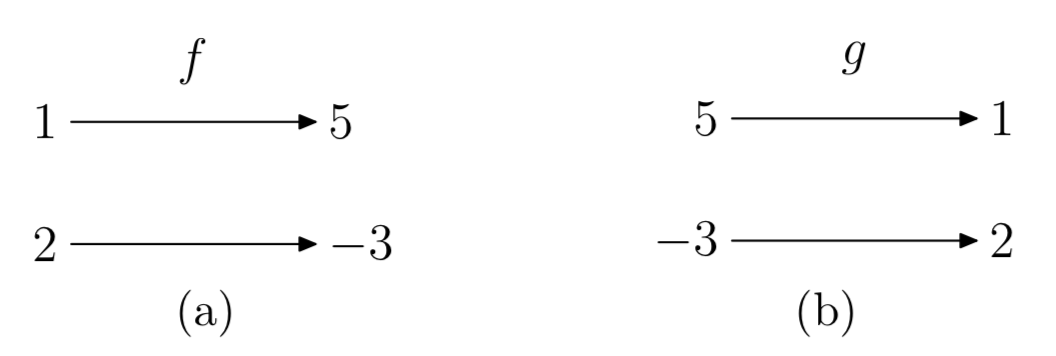
Dado que la función inversa g devuelve las salidas de f a sus entradas correspondientes, se deduce que las entradas de g son las salidas de f, y viceversa. Así, las funciones g y f se relacionan simplemente intercambiando sus entradas y salidas.
La función original debe ser uno a uno para tener una inversa. Por ejemplo, considere la función h en el Ejemplo 2. h no es uno a uno. Si invertimos las flechas en el diagrama de mapeo para h (ver Figura 1 (a)), entonces la relación resultante no será una función, porque 3 mapearía tanto a 1 como a 2.
Antes de dar la definición formal de una función inversa, es útil revisar la descripción de una función dada en la Sección 2.1. Si bien las funciones a menudo se definen por medio de una fórmula, recuerde que en general una función es solo una regla que dicta cómo asociar un valor de salida único a cada valor de entrada.
Definición\(\PageIndex{7}\)
Supongamos que f es una función dada uno a uno. La función inversa g se define de la siguiente manera: para cada y en el rango de f, defina g (y) para que sea el valor único x tal que y = f (x).
Para entender esta definición, es útil mirar un diagrama:
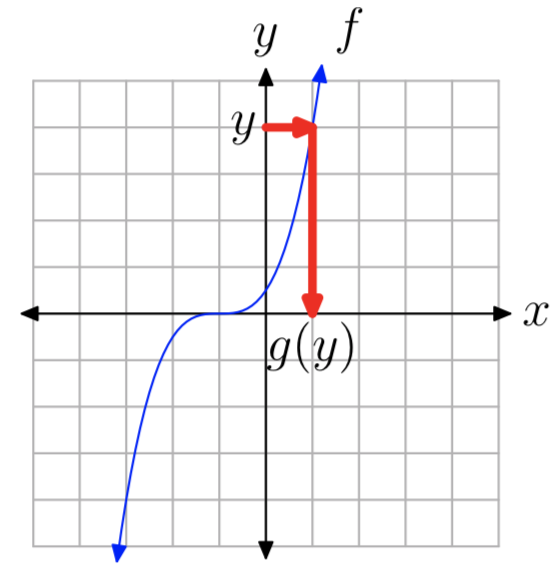
La entrada para g es cualquier valor y en el rango de f. Así, la entrada en el diagrama anterior es un valor en el eje y. La salida de g es el valor correspondiente en el eje x que satisface la condición y = f (x). Tenga en cuenta en particular que el valor x es único porque f es uno a uno.
La relación entre la función original f y su función inversa g se puede describir mediante:
PROPIEDAD\(\PageIndex{8}\)
Si g es la función inversa de f, entonces
\(x = g(y) \longleftrightarrow y = f(x)\).
De hecho, esta es realmente la relación definitoria para la función inversa. Una manera fácil de entender esta relación (y todo el concepto de una función inversa) es darse cuenta de que establece que las entradas y salidas se intercambian. Las entradas de g son las salidas de f, y viceversa. De ello se deduce que se intercambian el Dominio y Rango de f y g:
PROPIEDAD\(\PageIndex{9}\)
Si g es la función inversa de f, entonces
Dominio (g) = Rango (f) y Rango (g) = Dominio (f).
La relación definitoria en la Propiedad 8 también es equivalente a las dos identidades siguientes, por lo que estas proporcionan una caracterización alternativa de funciones inversas:
PROPIEDAD\(\PageIndex{10}\)
Si g es la función inversa de f, entonces
g (f (x)) = x por cada x en Dominio (f)
y
f (g (y)) = y para cada y en Dominio (g).
Tenga en cuenta que la primera declaración en la Propiedad 10 dice que g mapea la salida f (x) de nuevo a la entrada x. El segundo enunciado dice lo mismo con los roles de f y g invertidos. Por lo tanto, f y g deben ser inversas.
La propiedad 10 también puede interpretarse para decir que las funciones g y f se “deshacen” entre sí. Si primero aplicamos f a una entrada x, y luego aplicamos g, obtenemos x de nuevo. Asimismo, si aplicamos g a una entrada y, y luego aplicamos f, volvemos a obtener y. Entonces, sea cual sea la acción f que realice, g la invierte, y viceversa.
Ejemplo\(\PageIndex{11}\)
Supongamos\(f(x) = x^3\). Así, f es la función “cubing”. ¿Qué operación revertirá el proceso de cubing? Tomando una raíz cubicada. Así, la inversa de f debería ser la función\(g(y) = \sqrt[3]{y}\).
Verifiquemos Propiedad 10:
\(g(f(x))=g(x^3)= \sqrt[3]{x^3} = x\)
y
\(f(g(y)) = f(\sqrt[3]{y}) = (\sqrt[3]{y})^3 = y\)
Ejemplo\(\PageIndex{12}\)
Supongamos que f (x) = 4x−1. f actúa sobre una entrada x multiplicando primero por 4, y luego restando 1. La función inversa debe revertir el proceso: primero agregar 1, y luego dividir por 4. Así, la función inversa debería ser\(g(y) = \frac{y+1}{4}\).
Nuevamente, verifiquemos Propiedad 10:
\(g(f(x)) = g(4x−1) = \frac{(4x−1)+1}{4} = \frac{4x}{4} = x\)
y
\(f(g(y)) = f(\frac{y+1}{4}) = 4(\frac{y+1}{4})−1 = (y+1)−1 = y\)
Observaciones 13.
- El cálculo g (f (x)), en el que se usa la salida de una función como entrada de otra, se denomina la composición de g con f. Así, las funciones inversas se “deshacen” entre sí en el sentido de composición. La composición de funciones es un concepto importante en muchas áreas de las matemáticas, por lo que se proporciona más práctica con la composición de funciones en los ejercicios.
- Si g es la función inversa de f, entonces f es también la inversa de g. Esto se desprende de cualquiera de la Propiedad 8 o la Propiedad 10. (Tenga en cuenta que las etiquetas x e y para las variables no son importantes. La idea clave es que dos funciones sean inversas si se intercambian sus entradas y salidas).
Notación: Para indicar que dos funciones f y g son inversas, usualmente usamos la notación\(f^{−1}\) para g. El símbolo\(f^{−1}\) se lee “f reverse”. Además, para evitar confusiones con los roles típicos de x e y, a menudo es útil usar diferentes etiquetas para las variables. Reescribiendo la Propiedad 8 con la\(f^{−1}\) notación, y usando nuevas etiquetas para las variables, tenemos la relación definitoria:
PROPIEDAD\(\PageIndex{14}\)
\(v = f^{−1}(u) \longleftrightarrow u = f(v)\)
Así mismo, reescribiendo la Propiedad 10, tenemos las relaciones de composición:
PROPIEDAD\(\PageIndex{15}\)
\(f^{−1}(f(z))\)= z por cada z en el Dominio (f)
y
\(f(f^{−1}(z)) = z\)por cada z en Dominio (\(f^{−1}\))
Sin embargo, la nueva notación viene con una advertencia importante:
ADVERTENCIA\(\PageIndex{16}\)
\(f^{−1}\)no significa\(\frac{1}{f}\)
El exponente −1 es solo notación en este contexto. Cuando se aplica a una función, representa el inverso de la función, no el recíproco de la función.
La gráfica de una función inversa
¿Cómo son las gráficas de f y\(f^{−1}\) relacionadas? Supongamos que el punto (a, b) está en la gráfica de f. eso significa que b = f (a). Dado que las entradas y salidas se intercambian para la función inversa, se deduce que\(a = f^{−1}(b)\), entonces (b, a) está en la gráfica de\(f^{−1}\). Ahora (a, b) y (b, a) son solo reflexiones entre sí a través de la línea y = x (vea la discusión a continuación para una explicación detallada), por lo que se deduce que lo mismo es cierto de las gráficas de f y\(f^{−1}\) si graficamos ambas funciones en un mismo sistema de coordenadas (es decir, como funciones de x).
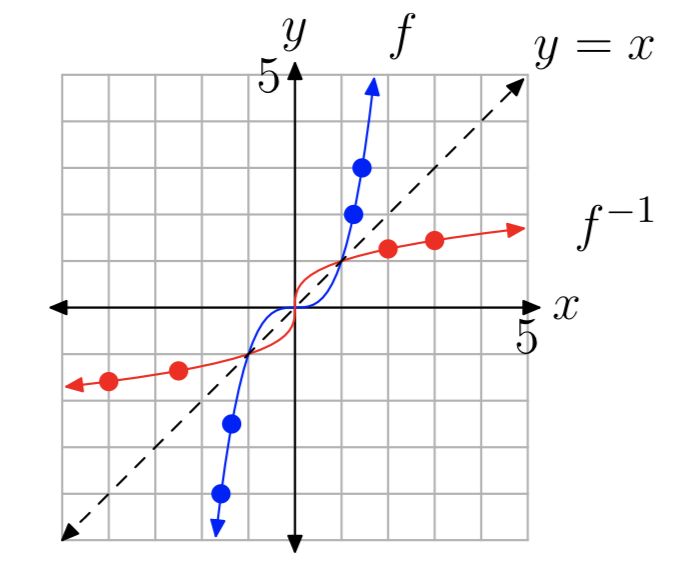
Por ejemplo, considere las funciones del Ejemplo 11. Las funciones\(f(x) = x^3\) y\(f^{−1}(x) = \sqrt[3]{x}\) se grafican en la Figura 6 junto con la línea y = x También se muestran varios pares de puntos reflejados en la gráfica.
Para ver por qué los puntos (a, b) y (b, a) son solo reflexiones entre sí a través de la línea y = x, considere el segmento S entre estos dos puntos (ver Figura 7). Bastará con mostrar: (1) que S es perpendicular a la línea y = x, y (2) que el punto de intersección P del segmento S y la línea y = x es equidistante de cada uno de (a, b) y (b, a).
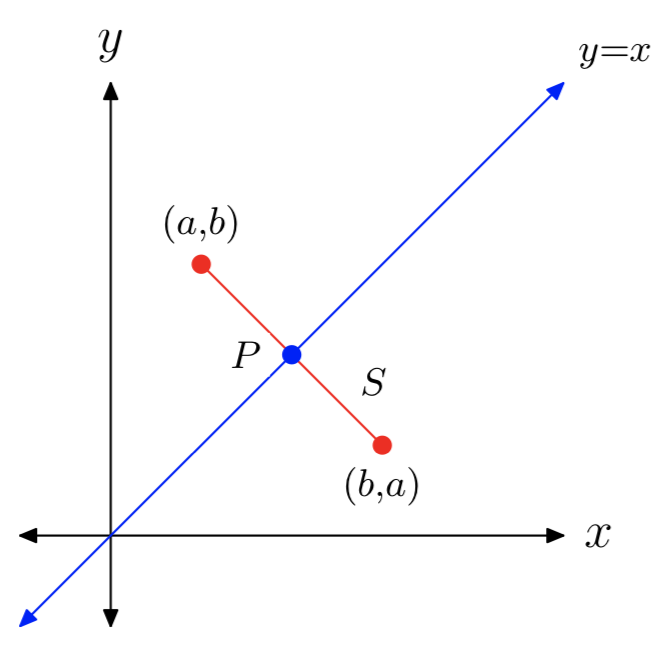
- La pendiente de S es
\(\frac{a−b}{b−a} = −1\),
y la pendiente de la línea y = x es 1, por lo que son perpendiculares.
2. La línea que contiene S tiene la ecuación y−b = − (x−a), o equivalentemente, y = −x+ (a+b). Para encontrar la intersección de S y la línea y = x, establezca x = −x+ (a+b) y resuelva x para obtener
\(x = \frac{a+b}{2}\).
Dado que y = x, se deduce que el punto de intersección es
\(P = (\frac{a+b}{2}, \frac{a+b}{2})\)
Finalmente, podemos usar la fórmula de distancia presentada en la sección 9.6 para calcular la distancia de P a (a, b) y la distancia de P a (b, a). En ambos casos, la distancia calculada resulta ser
\(\frac{|a−b|}{\sqrt{2}}\)
Computación de la fórmula de una función inversa
¿Cómo se encuentra la fórmula de una función inversa? En el Ejemplo 11, fue fácil ver que la inversa de la función “cubing” debe ser la función de raíz cúbica. Pero, ¿cómo se obtuvo la fórmula para la inversa en el Ejemplo 12?
En realidad, existe un procedimiento sencillo para encontrar la fórmula para la función inversa (siempre que exista tal fórmula; recuerde que no todas las funciones pueden describirse por una fórmula simple, por lo que el procedimiento no funcionará para tales funciones). El siguiente procedimiento funciona porque las entradas y salidas (las variables x e y) se conmutan en el paso 3.
Computación de la fórmula de una función inversa
- Verifique la gráfica de la función original f (x) para ver si pasa la prueba de línea horizontal. Si es así, entonces f es uno a uno y se puede proceder.
- Escribe la fórmula en forma de ecuación xi, como y = f (x).
- Intercambien las variables x e y.
- Resolver la nueva ecuación para y, si es posible. El resultado será la fórmula para\(f^{−1}(x)\).
Ejemplo\(\PageIndex{17}\)
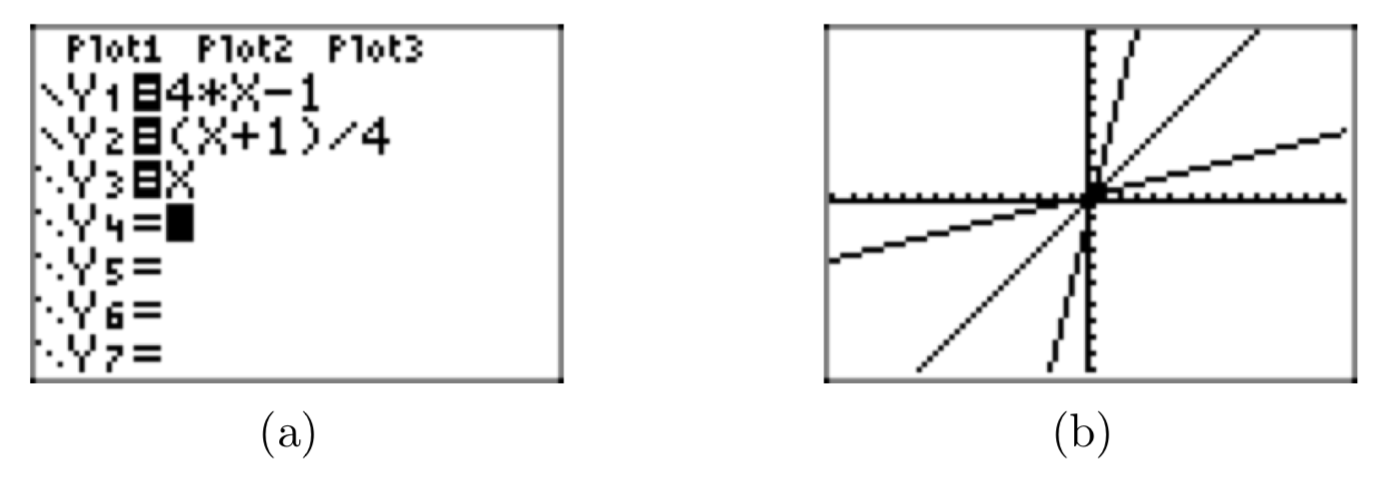
Empecemos por encontrar la inversa de la función f (x) = 4x−1 del Ejemplo 12.
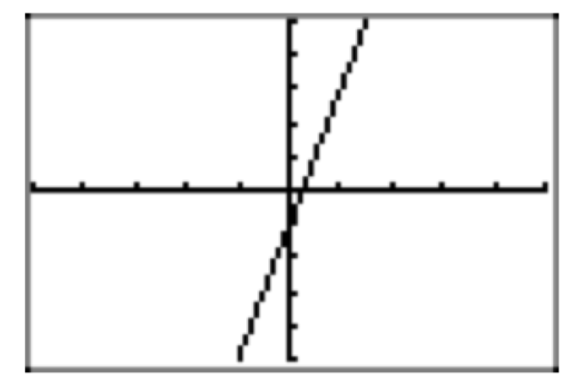
Paso 1: Una comprobación de la gráfica muestra que f es uno a uno (ver Figura 8).
PASO 2: Escribe la fórmula en forma de ecuación XY: y = 4x − 1
PASO 3: Intercambio x e y: x = 4y − 1
PASO 4: Resolver para y:
x = 4y − 1
\(\rightarrow x+1=4y\)
\(\rightarrow \frac{x+1}{4} = y\)
Por lo tanto,\(f^{−1}(x) = \frac{x+1}{4}\).
La Figura 9 demuestra que la gráfica de\(f^{−1}(x) = \frac{x+1}{4}\) es un reflejo de la gráfica de f (x) = 4x−1 a través de la línea y = x En esta figura, se ha utilizado el comando ZSquare en el menú ZOOM para ilustrar mejor la reflexión (el comando ZSquare ecualiza las escalas en ambos ejes).
Ejemplo\(\PageIndex{18}\)
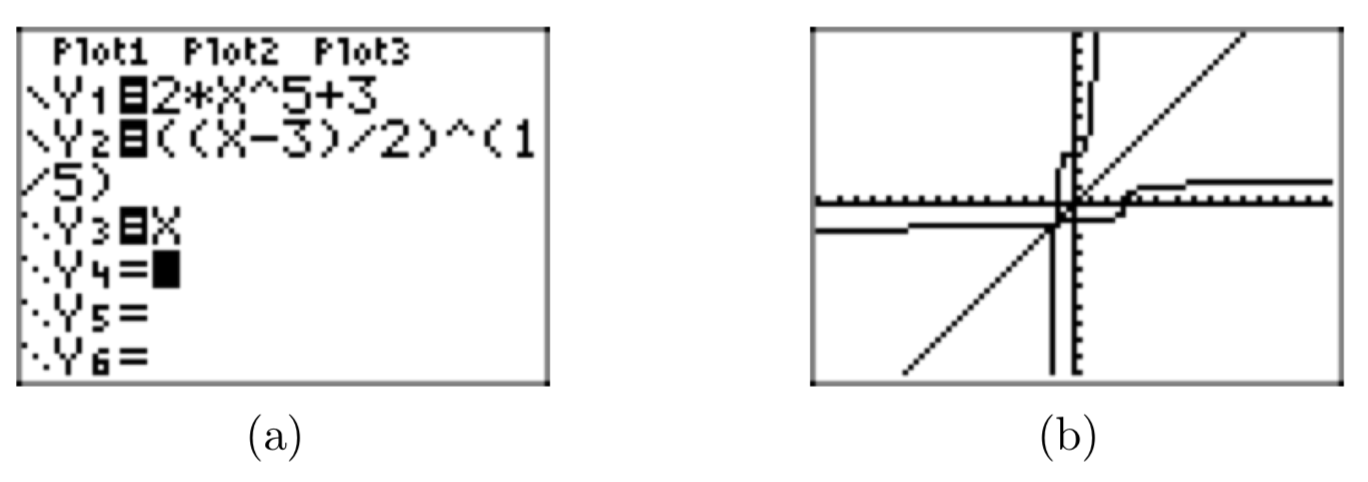
En esta ocasión encontraremos la inversa de\(f(x) = 2x^5+3\).
Paso 1: Una comprobación de la gráfica muestra que f es uno a uno (esto se deja para que el lector lo verifique).
PASO 2: Escribe la fórmula en forma de ecuación XY:\(y = 2x^5+3\).
PASO 3: Intercambio x e y:\(x = 2y^5+3\).
PASO 4: Resolver para y:
\(x = 2y^5+3\).
\(\rightarrow x−3 = 2y^5\)
\(\rightarrow \frac{x−3}{2} = y^5\)
\(\rightarrow \sqrt[5]{\frac{x−3}{2}} = y\)
Por lo tanto,\(f^{−1}(x) = \sqrt[5]{\frac{x−3}{2}}\)
Nuevamente, tenga en cuenta que la gráfica de\(f^{−1}(x) = \sqrt[5]{\frac{x−3}{2}}\) es un reflejo de la gráfica de\(f(x) = 2x^5+3\) a través de la línea y = x (ver Figura 10).
Ejemplo\(\PageIndex{19}\)
Encuentra la inversa de\(f(x) = \frac{5}{7+x}\).
Paso 1: Una comprobación de la gráfica muestra que f es uno a uno (esto se deja para que el lector lo verifique).
PASO 2: Escribe la fórmula en forma de ecuación XY:\(y = \frac{5}{7+x}\).
PASO 3: Intercambio x e y:\(x = \frac{5}{7+y}\).
PASO 4: Resolver para y:
\(x = \frac{5}{7+y}\)
\(\rightarrow x(7+y) = 5\)
\(\rightarrow 7+y = \frac{5}{x}\)
\(y = \frac{5}{x}−7 = \frac{5 − 7x}{x}\)
Por lo tanto,\(f^{−1}(x) = \frac{5 − 7x}{x}\)
Ejemplo\(\PageIndex{20}\)
Este ejemplo es un poco más complicado: encontrar la inversa de la función\(f(x) = \frac{5x+2}{x−3}\).
Paso 1: Una comprobación de la gráfica muestra que f es uno a uno (esto se deja para que el lector lo verifique).
PASO 2: Escribe la fórmula en forma de ecuación XY:\(y = \frac{5x+2}{x−3}\).
PASO 3: Intercambio x e y:\(x = \frac{5y+2}{y−3}\).
PASO 4: Resolver para y:
\(x = \frac{5y+2}{y−3}\)
\(\rightarrow x(y−3) = 5y+2\)
\(\rightarrow xy−3x = 5y+2\)
Esta ecuación es lineal en y. Aísle los términos que contienen la variable y en un lado de la ecuación, factor, luego divídalo por el coeficiente de y.
\(xy−3x = 5y+2\)
\(xy−5y = 3x+2\)
\(y(x−5) = 3x+2\)
\(y = \frac{3x+2}{x−5}\)
Por lo tanto,\(f^{−1}(x) = \frac{3x+2}{x−5}\).
Ejemplo\(\PageIndex{21}\)
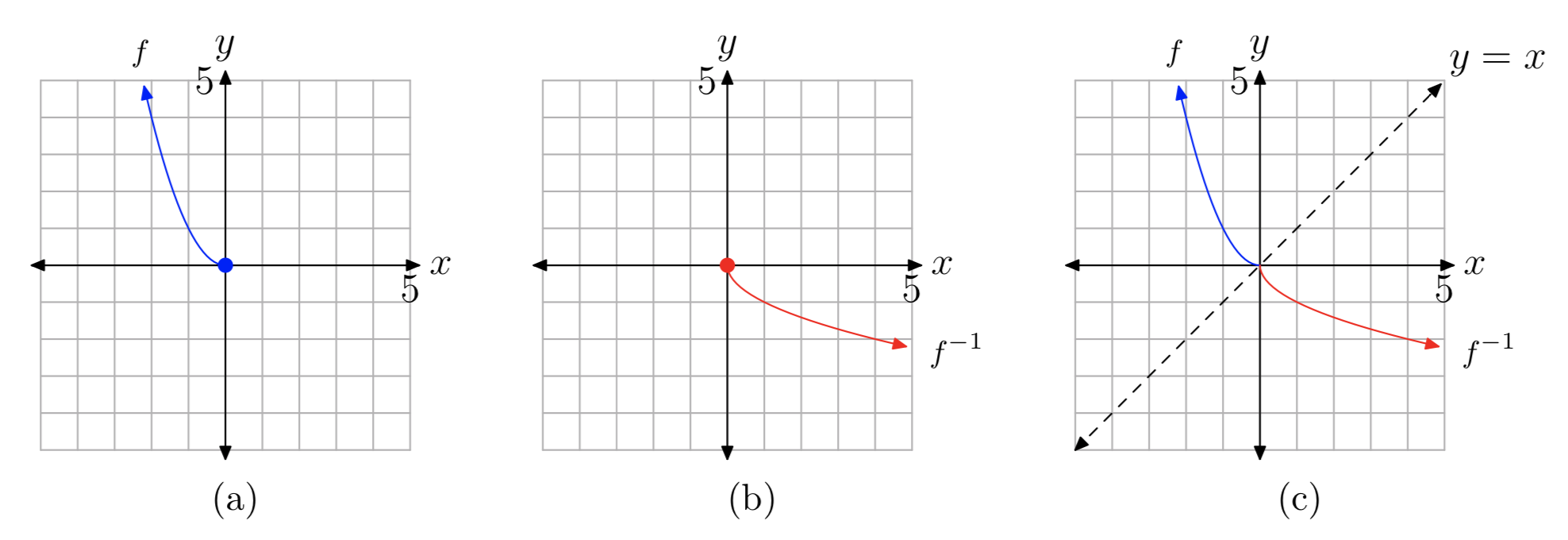
Según la prueba de línea horizontal, la función ciertamente no\(h(x) = x^2\) es uno a uno. Sin embargo, si solo consideramos la mitad derecha o la mitad izquierda de la función (es decir, restringir el dominio ya sea al intervalo\([0, \infty)\) o\((−\infty,0]\)), entonces la función sería uno a uno, y por lo tanto tendría una inversa (Figura 11 (a) muestra la mitad izquierda). Por ejemplo, supongamos que f es la función\(f(x) = x^2\),\(x \le 0\)
En este caso, el procedimiento sigue funcionando, siempre que llevemos consigo la condición de dominio en todos los pasos, de la siguiente manera:
Paso 1: La gráfica de la Figura 11 (a) pasa la prueba de línea horizontal, por lo que f es uno a uno.
Paso 2: Escribe la fórmula en forma de ecuación XY:\(y = x^2\),\(x \le 0\)
Paso 3: Intercambio x e y:\(x = y^2\),\(y \le 0\)
Observe cómo x e y también deben intercambiarse en la condición de dominio.
Paso 4: Resolver para y:\(y = \pm \sqrt{x}\),\(y \le 0\)
Ahora hay dos opciones para y, una positiva y otra negativa, pero la condición nos\(y \le 0\) dice que la elección negativa es la correcta. Así, el último enunciado equivale a
\(y = −\sqrt{x}\).
Por lo tanto,\(f^{−1}(x) = −\sqrt{x}\). La gráfica de\(f^{−1}\) se muestra en la Figura 11 (b), y las gráficas de ambos f y se\(f^{−1}\) muestran en la Figura 11 (c) como reflexiones a través de la línea y = x.
Ejercicio
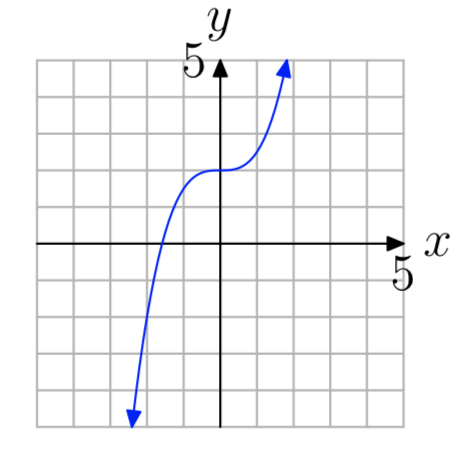
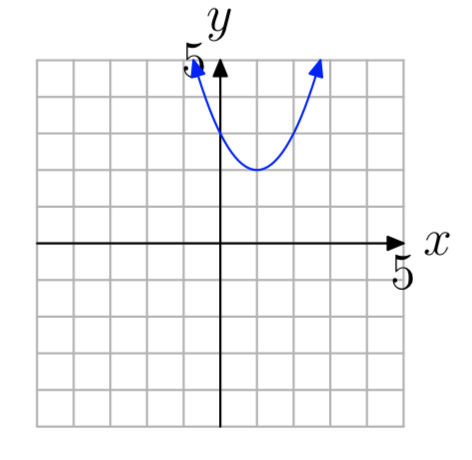
En los Ejercicios 1 - 12, utilice la gráfica para determinar si la función es uno a uno.
Ejercicio\(\PageIndex{1}\)
- Contestar
-
no uno a uno
Ejercicio\(\PageIndex{2}\)
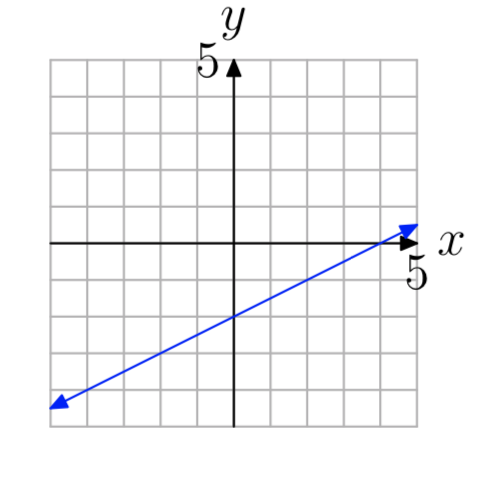
Ejercicio\(\PageIndex{3}\)
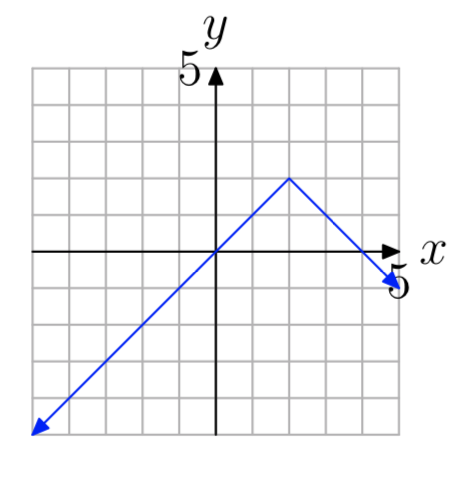
- Contestar
-
no uno a uno
Ejercicio\(\PageIndex{4}\)
Ejercicio\(\PageIndex{5}\)
- Contestar
-
no uno a uno
Ejercicio\(\PageIndex{6}\)
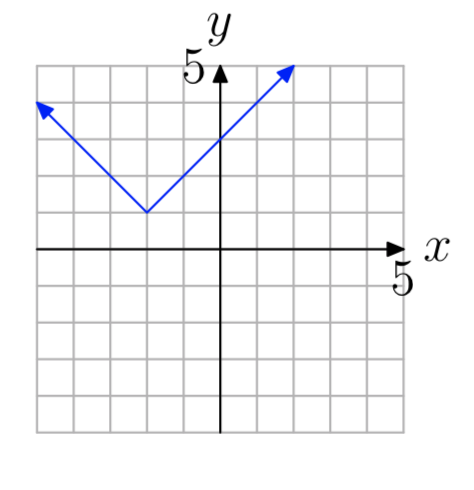
Ejercicio\(\PageIndex{7}\)
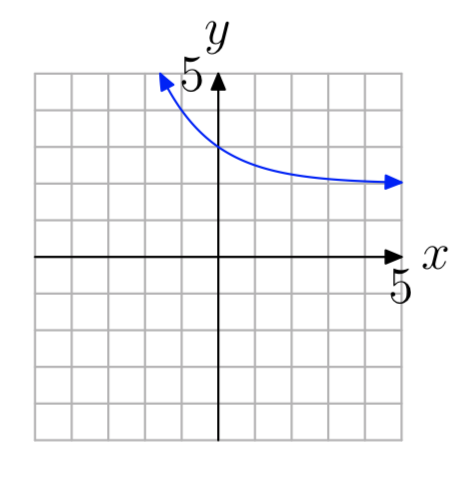
- Contestar
-
uno a uno
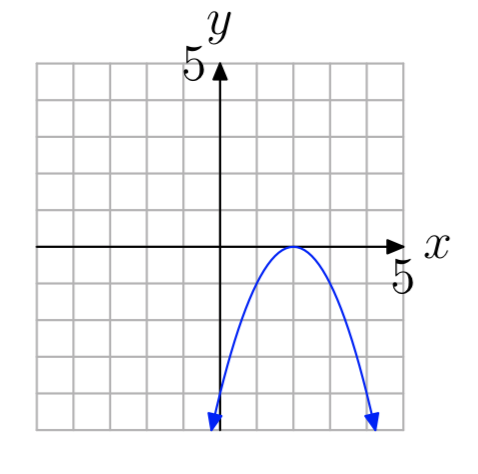
Ejercicio\(\PageIndex{8}\)
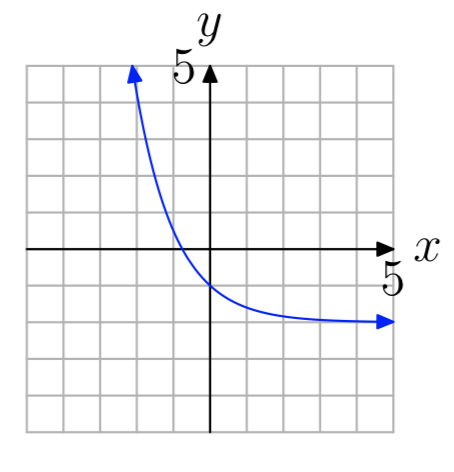
Ejercicio\(\PageIndex{9}\)
- Contestar
-
uno a uno
Ejercicio\(\PageIndex{10}\)
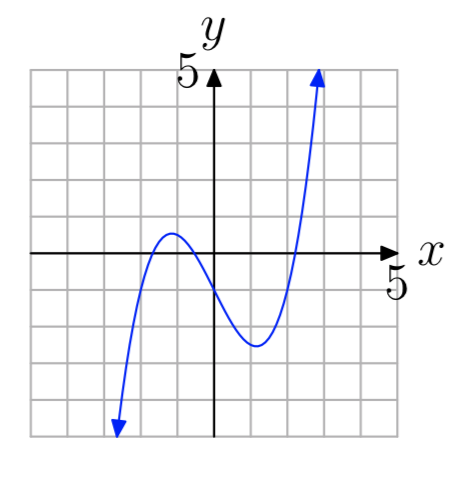
Ejercicio\(\PageIndex{11}\)
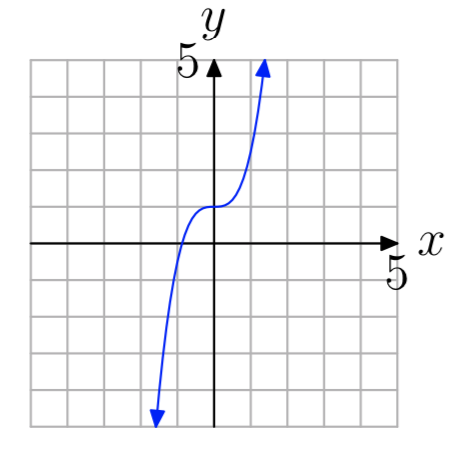
- Contestar
-
uno a uno
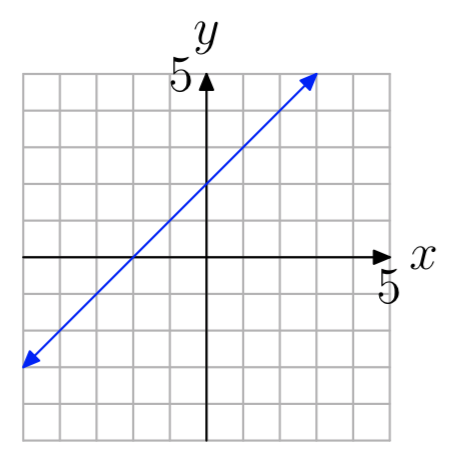
Ejercicio\(\PageIndex{12}\)
En los Ejercicios 13 - 28, evalúa la composición g (f (x)) y simplifica tu respuesta.
Ejercicio\(\PageIndex{13}\)
\(g(x) = \frac{9}{x}\),\(f(x) = −2x^2+5x−2\)
- Contestar
-
\(\frac{−9}{2x^2−5x+2}\)
Ejercicio\(\PageIndex{14}\)
\(f(x) = −\frac{5}{x}\),\(g(x) = −4x^2+x−1\)
Ejercicio\(\PageIndex{15}\)
\(g(x) = 2\sqrt{x}\),\(f(x)=−x−3\)
- Contestar
-
\(2\sqrt{−x−3}\)
Ejercicio\(\PageIndex{16}\)
\(f(x) = 3x^2−3x−5\),\(g(x) = \frac{6}{x}\)
Ejercicio\(\PageIndex{17}\)
\(g(x) = 3\sqrt{x}\),\(f(x) = 4x+1\)
- Contestar
-
\(3\sqrt{4x+1}\)
Ejercicio\(\PageIndex{18}\)
f (x) = −3x−5, g (x) =−x−2
Ejercicio\(\PageIndex{19}\)
\(g(x) = −5x^2+3x−4\),\(f(x) = \frac{5}{x}\)
- Contestar
-
\(−\frac{125}{x^2}+\frac{15}{x}−4\)
Ejercicio\(\PageIndex{20}\)
g (x) = 3x+3,\(f(x) = 4x^2 −2x−2\)
Ejercicio\(\PageIndex{21}\)
\(g(x) = 6\sqrt{x}\), f (x) = −4x+4
- Contestar
-
\(6\sqrt{−4x+4}\)
Ejercicio\(\PageIndex{22}\)
g (x) = 5x−3, f (x) =−2x−4
Ejercicio\(\PageIndex{23}\)
\(g(x) = 3\sqrt{x}\), f (x) = −2x+1
- Contestar
-
\(3\sqrt{−2x+1}\)
Ejercicio\(\PageIndex{24}\)
\(g(x) = \frac{3}{x}\),\(f(x)=−5x^2−5x−4\)
Ejercicio\(\PageIndex{25}\)
\(f(x)=\frac{5}{x}\), g (x) =−x+1
- Contestar
-
\(−\frac{5}{x}+1\)
Ejercicio\(\PageIndex{26}\)
\(f(x) = 4x^2+3x−4\),\(g(x) = \frac{2}{x}\)
Ejercicio\(\PageIndex{27}\)
g (x) = −5x+1, f (x) = −3x−2
- Contestar
-
15x+11
Ejercicio\(\PageIndex{28}\)
\(g(x) = 3x^2 +4x−3\),\(f(x)=\frac{8}{x}\)
En los Ejercicios 29 - 36, primero copia la gráfica dada de la función uno-a-uno f (x) en tu papel cuadriculado. Después en el mismo sistema de coordenadas, esbozar la gráfica de la función inversa\(f^{−1}(x)\).
Ejercicio\(\PageIndex{29}\)
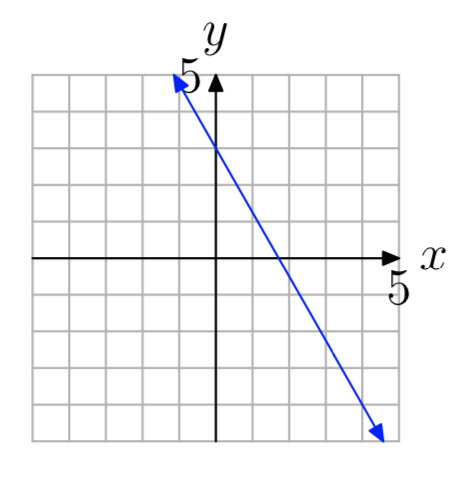
- Contestar
-
Ejercicio\(\PageIndex{30}\)
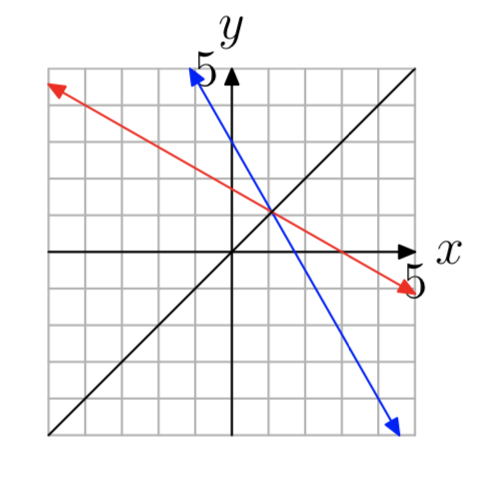
Ejercicio\(\PageIndex{31}\)
- Contestar
-
Ejercicio\(\PageIndex{32}\)
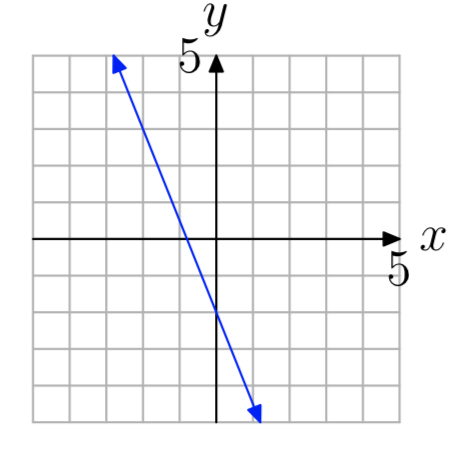
Ejercicio\(\PageIndex{33}\)
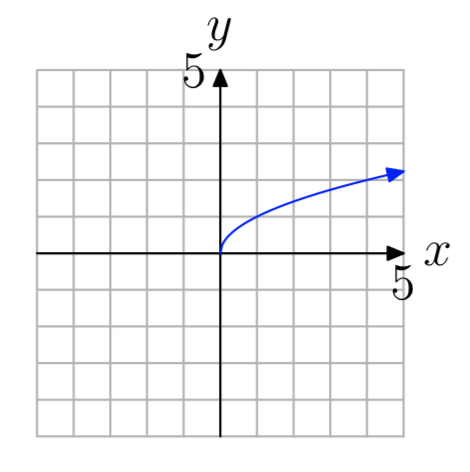
- Contestar
-
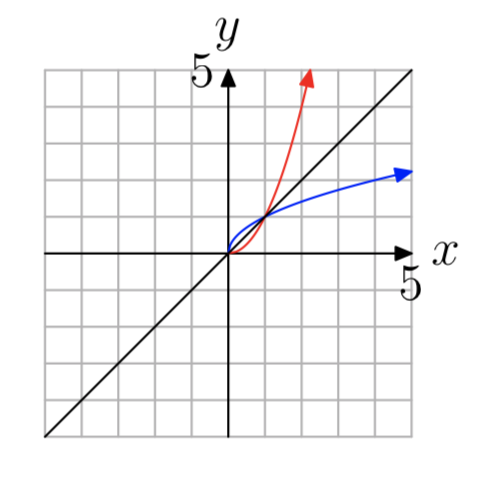
Ejercicio\(\PageIndex{34}\)
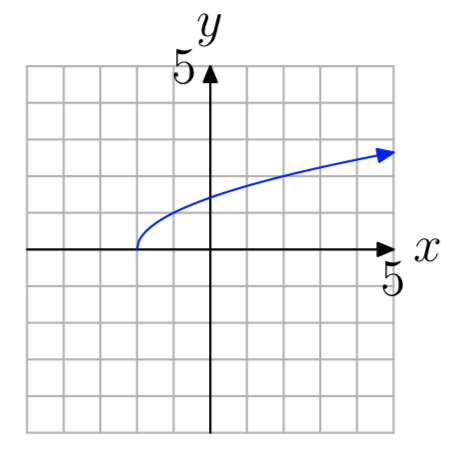
Ejercicio\(\PageIndex{35}\)
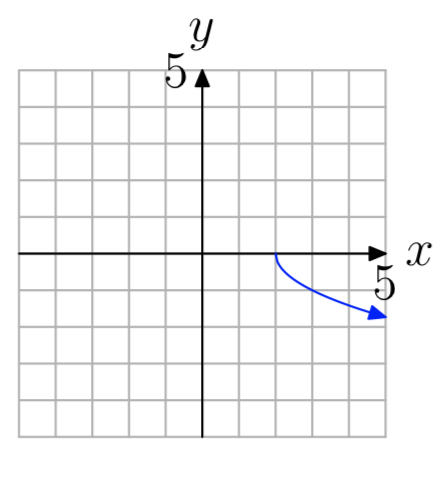
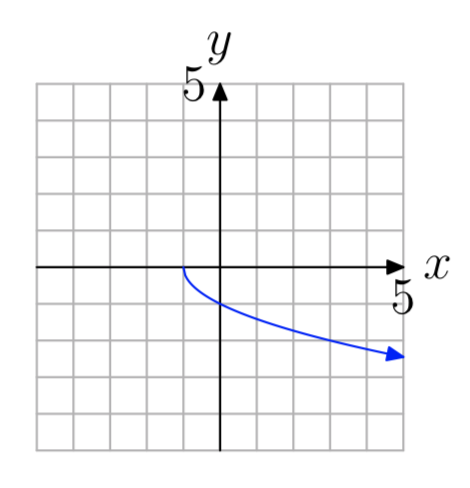
- Contestar
-
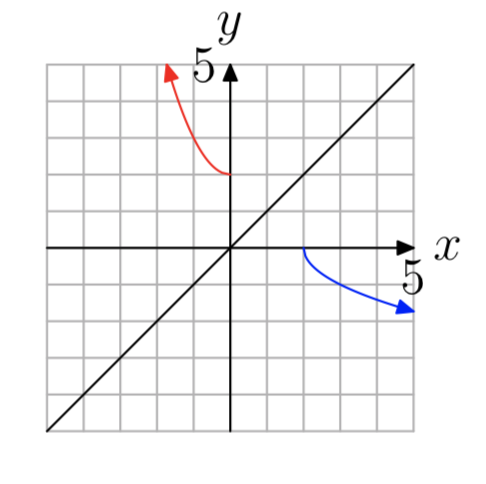
Ejercicio\(\PageIndex{36}\)
En Ejercicios 37 - 68, encuentra la fórmula para la función inversa\(f^{−1}(x)\).
Ejercicio\(\PageIndex{37}\)
\(f(x) = 5x^3−5\)
- Contestar
-
\(\sqrt[3]{\frac{x+5}{5}}\)
Ejercicio\(\PageIndex{38}\)
\(f(x) = 4x^7−3\)
Ejercicio\(\PageIndex{39}\)
\(f(x)=−\frac{9x−3}{7x+6}\)
- Contestar
-
\(−\frac{6x−3}{7x+9}\)
Ejercicio\(\PageIndex{40}\)
f (x) = 6x−4
Ejercicio\(\PageIndex{41}\)
f (x) = 7x−9
- Contestar
-
\(\frac{x+9}{7}\)
Ejercicio\(\PageIndex{42}\)
f (x) = 7x+4
Ejercicio\(\PageIndex{43}\)
\(f(x) = 3x^5−9\)
- Contestar
-
\(\sqrt[5]{\frac{x+9}{3}}\)
Ejercicio\(\PageIndex{44}\)
f (x) = 6x+7
Ejercicio\(\PageIndex{45}\)
\(f(x) = \frac{4x+2}{4x+3}\)
- Contestar
-
\(−\frac{3x−2}{4x−4}\)
Ejercicio\(\PageIndex{46}\)
\(f(x) = 5x^7+4\)
Ejercicio\(\PageIndex{47}\)
\(f(x) = \frac{4x−1}{2x+2}\)
- Contestar
-
\(−\frac{2x+1}{2x−4}\)
Ejercicio\(\PageIndex{48}\)
\(f(x) = \sqrt[7]{8x−3}\)
Ejercicio\(\PageIndex{49}\)
\(f(x) = \sqrt[3]{−6x−4}\)
- Contestar
-
\(−\frac{x^3+4}{6}\)
Ejercicio\(\PageIndex{50}\)
\(f(x) = \frac{8x−7}{3x−6}\)
Ejercicio\(\PageIndex{51}\)
\(f(x) = \sqrt[7]{−3x−5}\)
- Contestar
-
\(−\frac{x^7+5}{3}\)
Ejercicio\(\PageIndex{52}\)
\(f(x) = \sqrt[9]{8x+2}\)
Ejercicio\(\PageIndex{53}\)
\(f(x) = \sqrt[3]{6x+7}\)
- Contestar
-
\(\frac{x^3−7}{6}\)
Ejercicio\(\PageIndex{54}\)
\(f(x) = \frac{3x+7}{2x+8}\)
Ejercicio\(\PageIndex{55}\)
f (x) = −5x+2
- Contestar
-
\(−\frac{x−2}{5}\)
Ejercicio\(\PageIndex{56}\)
f (x) = 6x+8
Ejercicio\(\PageIndex{57}\)
\(f(x) = 9x^9+5\)
- Contestar
-
\(\sqrt[9]{\frac{x−5}{9}}\)
Ejercicio\(\PageIndex{58}\)
\(f(x) = 4x^5−9\)
Ejercicio\(\PageIndex{59}\)
\(f(x) = \frac{9x−3}{9x+7}\)
- Contestar
-
\(−\frac{7x+3}{9x−9}\)
Ejercicio\(\PageIndex{60}\)
\(f(x) = \sqrt[3]{9x−7}\)
Ejercicio\(\PageIndex{61}\)
\(f(x) = x^4\),\(x \le 0\)
- Contestar
-
\(−\sqrt[4]{x}\)
Ejercicio\(\PageIndex{62}\)
\(f(x) = x^4\),\(x \ge 0\)
Ejercicio\(\PageIndex{63}\)
\(f(x) = x^2−1\),\(x \le 0\)
- Contestar
-
\(−\sqrt{x+1}\)
Ejercicio\(\PageIndex{64}\)
\(f(x) = x^2+2\),\(x \ge 0\)
Ejercicio\(\PageIndex{65}\)
\(f(x) = x^4+3\),\(x \le 0\)
- Contestar
-
\(−\sqrt[4]{x−3}\)
Ejercicio\(\PageIndex{66}\)
\(f(x) = x^4−5\),\(x \ge 0\)
Ejercicio\(\PageIndex{67}\)
\(f(x) = (x−1)^2\),\(x \le 1\)
- Responder
-
\(−\sqrt{x}+1\)
Ejercicio\(\PageIndex{68}\)
\(f(x) = (x+2)^2\),\(x \ge −2\)


