1.4: Fracciones

Última actualización
Guardar como PDF

Page ID: 110104

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Reducir una fracción a los términos más bajos.
Multiplicar y dividir fracciones.
Sumar y restar fracciones.

Reduciendo

Una fracción es un número real escrito como cociente, o ratio, de dos enteros$a$ y$b$, donde$b \neq 0$.

https://2012books.lardbucket.org/books/beginning-algebra/section_04/c1e301b3aeb14755a7739e70039397e5.jpg — Figura$\PageIndex{1}$

El entero por encima de la barra de fracciones se llama numerador y el entero de abajo se llama denominador. El numerador a menudo se llama la “parte” y el denominador a menudo se llama el “todo”. Las fracciones equivalentes son dos proporciones iguales expresadas usando diferentes numeradores y denominadores. Por ejemplo,

$\frac{50}{100} = \frac{1}{2}$

Cincuenta partes de$100$ es la misma proporción que$1$ parte de$2$ y representa el mismo número real. Considere las siguientes factorizaciones de$50$ y$100$:

\ [
\ begin {align*}
50 &= 2\ cdot 25\\
100 &= 4\ cdot 25
\ end {alinear*}
\]

Los números$50$ y$100$ compartir el factor$25$. Un factor compartido se denomina factor común. Podemos reescribir la relación de la$\frac{50}{100}$ siguiente manera:

$\frac{50}{100} = \frac{2 \cdot 25}{4 \cdot 25}$

Haciendo uso de la propiedad de identidad multiplicativa y el hecho de que$\frac{25}{25} = 1$, tenemos

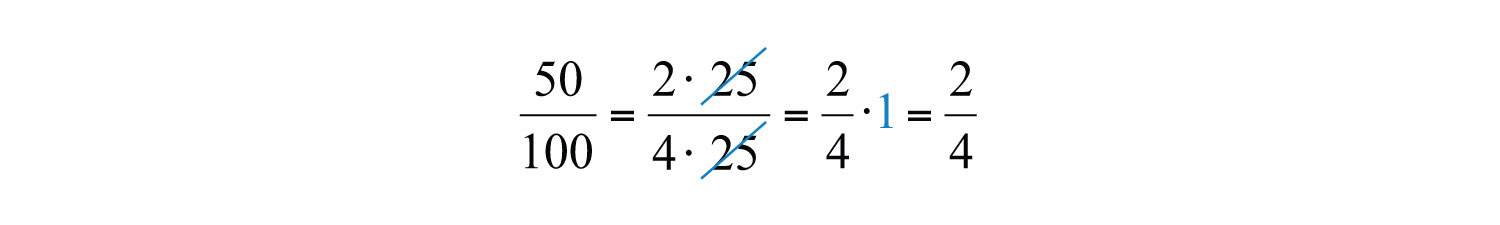
https://2012books.lardbucket.org/books/beginning-algebra/section_04/816c8d43ed965635bd35d214dbae6ff6.jpg — Figura$\PageIndex{2}$

Dividir$\frac{25}{25}$ y reemplazar este factor por a$1$ se llama cancelar. Juntos, estos pasos básicos para encontrar fracciones equivalentes definen el proceso de reducción. Dado que los factores dividen su producto de manera uniforme, logramos el mismo resultado dividiendo tanto el numerador$25$ como el denominador por lo siguiente:

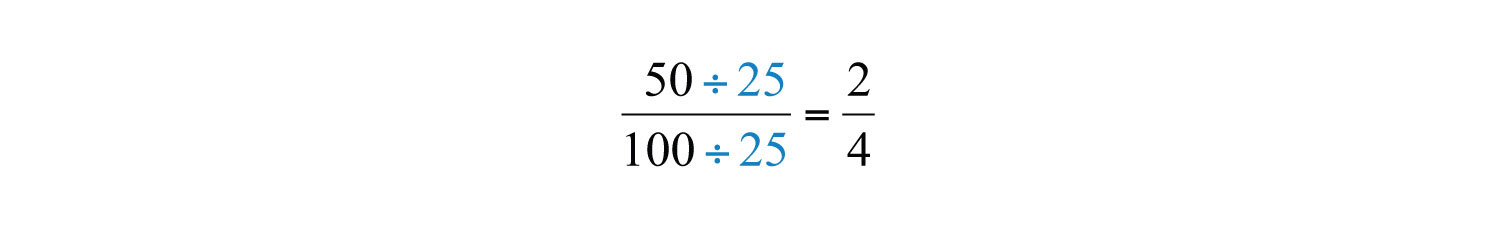
https://2012books.lardbucket.org/books/beginning-algebra/section_04/42c81fdfeeb3ed9a39c98455ca98e998.jpg — Figura$\PageIndex{3}$

Encontrar fracciones equivalentes donde el numerador y el denominador no tienen otro factor común que no$1$ sea llamado reducir a términos más bajos. Al aprender a reducir a términos más bajos, es útil primero reescribir el numerador y denominador como producto de primos y luego cancelar. Por ejemplo,

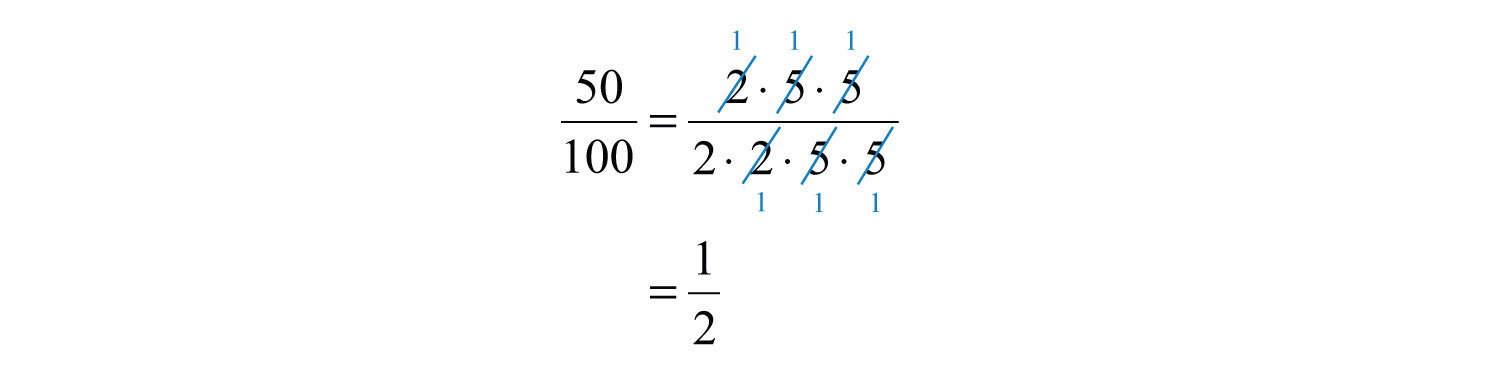
https://2012books.lardbucket.org/books/beginning-algebra/section_04/ba0ba7c8c9ef5331d11eb7d618f0406c.jpg — Figura$\PageIndex{4}$

Logramos el mismo resultado dividiendo el numerador y el denominador por el mayor factor común (GCF). El GCF es el número más grande que divide tanto el numerador como el denominador de manera uniforme. Una forma de encontrar el GCF de$50$ y$100$ es enumerar todos los factores de cada uno e identificar el mayor número que aparece en ambas listas. Recuerde, cada número es también un factor de sí mismo.

\ [
\ begin {alinear*}
&\ {1,2,5,10,25,50\} &&\ color {cerúleo} {Factores\ de\ 50}\\
&\ {1,2,4,5,10,20,25,50,100\} &&\ color {cerúleo} {Factores\ de\ 100}
\ end {alinear*}
\]

Los factores comunes se enumeran en negrita, y vemos que el mayor factor común es$50$. Utilizamos la siguiente notación para indicar el GCF de dos números: GCF$(50, 100) = 50$. Después de determinar el GCF, reduzca dividiendo tanto el numerador como el denominador de la siguiente manera:

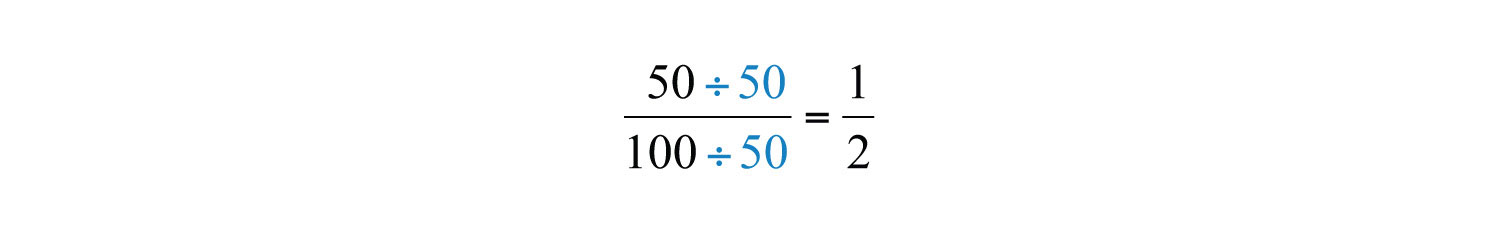
https://2012books.lardbucket.org/books/beginning-algebra/section_04/da8c2537d2e0becc19c6b6d9d2517bd9.jpg — Figura$\PageIndex{5}$

Ejemplo$\PageIndex{1}$

Reducir a los términos más bajos:$\frac{105}{300}$.

Solución

Reescribe el numerador y denominador como producto de primos y luego cancela.

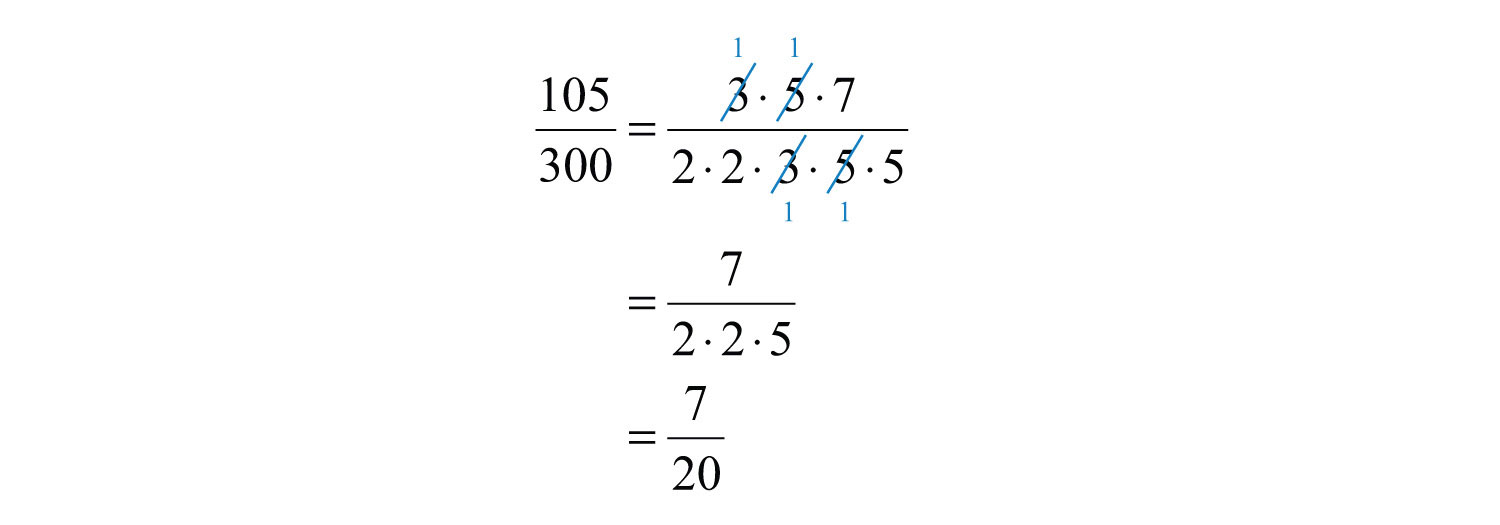
https://2012books.lardbucket.org/books/beginning-algebra/section_04/a283352804bf0e1ae71474ec35d5c5a0.jpg — Figura$\PageIndex{6}$

Alternativamente, logramos el mismo resultado si dividimos tanto el numerador como el denominador por el GCF$(105, 300)$. Una manera rápida de encontrar el GCF de los dos números requiere que primero escribamos cada uno como producto de primos. El GCF es el producto de todos los factores primos comunes.

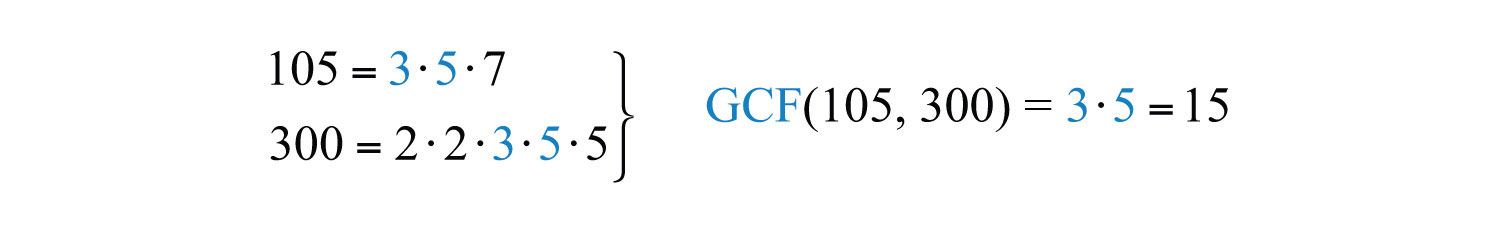
https://2012books.lardbucket.org/books/beginning-algebra/section_04/1cf2ffbc0bd4b0ab042ad9ee67da23a5.jpg — Figura$\PageIndex{7}$

En este caso, los factores primos comunes son$3$ y$5$ y el mayor factor común de$105$ y$300$ es$15$.

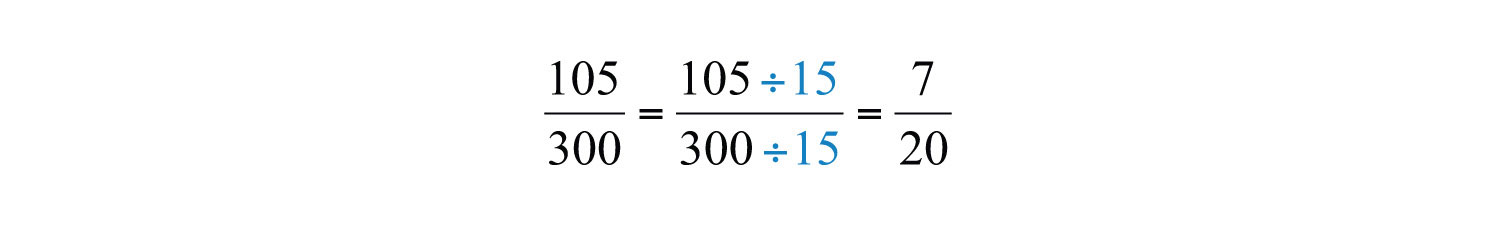
https://2012books.lardbucket.org/books/beginning-algebra/section_04/76d1cd06699f306be99ea2f093343579.jpg — Figura$\PageIndex{8}$

Respuesta:

$\frac{7}{20}$

Ejemplo$\PageIndex{2}$

¡Prueba esto! Reducir a los términos más bajos:$\frac{32}{96}$.

Solución de video:

(haga clic para ver el video)

Una fracción impropia es aquella en la que el numerador es mayor que el denominador. Un número mixto es un número que representa la suma de un número entero y una fracción. Por ejemplo,$5 \frac{1}{2}$ es un número mixto que representa la suma$5+\frac{1}{2}$. Utilice la división larga para convertir una fracción impropia en un número mixto; el resto es el numerador de la parte fraccionaria.

Ejemplo$\PageIndex{3}$

Escribir$\frac{23}{5}$ como un número mixto.

Solución

Observe que se$5$ divide en$23$ cuatro veces con un resto de$3$.

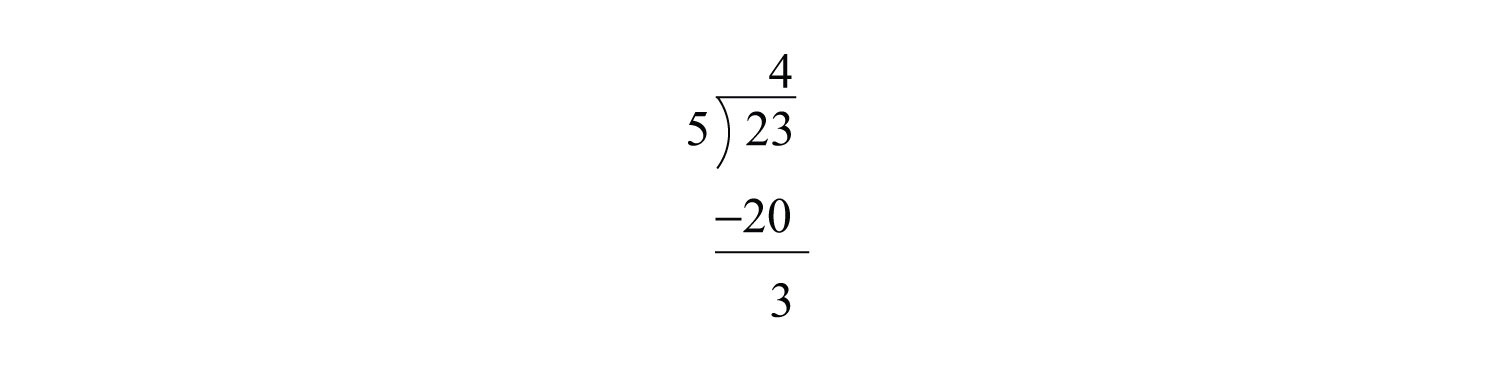
https://2012books.lardbucket.org/books/beginning-algebra/section_04/43599ed7529b52ba25c9d47182e730c0.jpg — Figura$\PageIndex{9}$

Entonces podemos escribir

\ [
\ begin {align*}
\ frac {23} {5} &= 4 +\ frac {3} {5}\\
&= 4\ frac {3} {5}
\ end {align*}
\]

Tenga en cuenta que el denominador de la parte fraccionaria del número mixto sigue siendo el mismo que el denominador de la fracción original.

Responder

$4 \frac{3}{5}$

Para convertir números mixtos en fracciones impropias, multiplica el número entero por el denominador y luego suma el numerador; escribe este resultado sobre el denominador original.

Ejemplo$\PageIndex{4}$

Escribir$3 \frac{5}{7}$ como una fracción impropia.

Solución

Obtener el numerador multiplicando$7$ tiempos$3$ y luego sumar$5$.

\ [
\ begin {align*}
3\ frac {5} {7} &=\ frac {7\ cdot 3 + 5} {7}\\
&=\ frac {21+5} {7}\\
&=\ frac {26} {7}
\ end {align*}
\]

Responder

$\frac{26}{7}$

Es importante señalar que convertir a un número mixto no es parte del proceso de reducción. Consideramos que fracciones impropias$267$, como, se reducen a términos más bajos. En álgebra suele ser preferible trabajar con fracciones impropias, aunque en algunas aplicaciones, los números mixtos son más apropiados.

Ejemplo$\PageIndex{5}$

¡Prueba esto! Convertir$10 \frac{1}{2}$ a una fracción impropia.

Solución

(haga clic para ver el video)

Multiplicar y dividir fracciones

En esta sección, supongamos que$a, b, c$, y$d$ son todos enteros distintos de cero. El producto de dos fracciones es la fracción formada por el producto de los numeradores y el producto de los denominadores. Es decir, para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores:

$\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}$

Ejemplo$\PageIndex{6}$

Multiplicar:$\frac{2}{3} \cdot \frac{5}{7}$

Solución

Multiplicar los numeradores y multiplicar los denominadores.

\ [
\ begin {align*}
\ frac {2} {3}\ cdot\ frac {5} {7} &=\ frac {2\ cdot 5} {3\ cdot 7}\\
&=\ frac {10} {21}
\ end {align*}
\]

Respuesta:

$\frac{10}{21}$

Ejemplo$\PageIndex{7}$

Multiplicar:$\frac{5}{9}\left(-\frac{1}{4}\right)$

Solución

Recordemos que el producto de un número positivo y un número negativo es negativo.

\ [
\ begin {align*}
\ frac {5} {9}\ izquierda (-\ frac {1} {4}\ derecha) &= -\ frac {5\ cdot 1} {9\ cdot 4}\\
&= -\ frac {5} {36}
\ end {align*}
\]

Respuesta:

$-\frac{5}{36}$

Ejemplo$\PageIndex{8}$

Multiplicar:$\frac{2}{3} \cdot 5 \frac{3}{4}$

Solución

Comience por convertir$5 \frac{3}{4}$ a una fracción impropia.

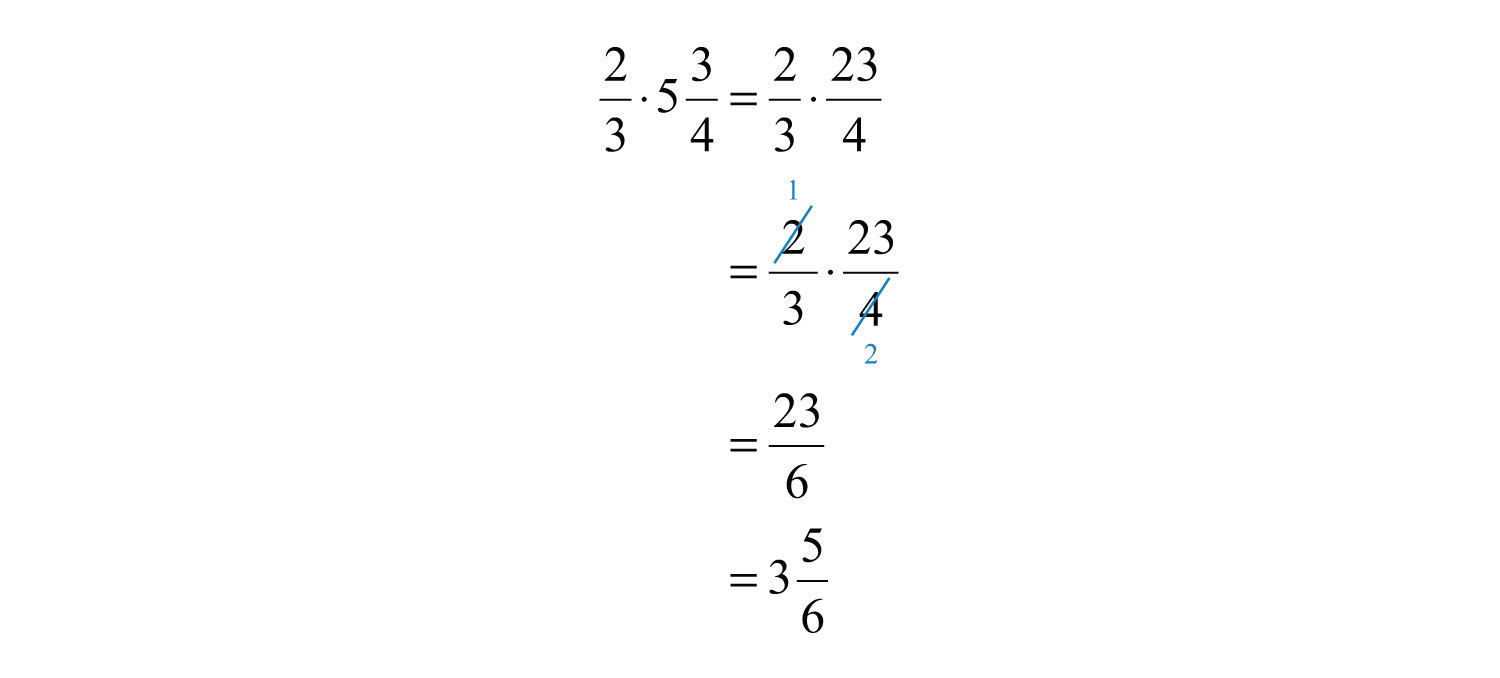
https://2012books.lardbucket.org/books/beginning-algebra/section_04/f4ca5608dcb974eb1306d19b4b1ab7b1.jpg — Figura$\PageIndex{10}$

En este ejemplo, notamos que podíamos reducir antes de multiplicar los numeradores y los denominadores. Reducir de esta manera se llama cancelación cruzada, y puede ahorrar tiempo al multiplicar fracciones.

Responder

$3 \frac{5}{6}$

Dos números reales cuyo producto es$1$ se llaman reciprocales. Por lo tanto,$\frac{a}{b}$ y$\frac{b}{a}$ son recíprocos porque$ \frac{a}{b} \cdot \frac{b}{a} = \frac{ab}{ab} = 1$. Por ejemplo,

$\frac{2}{3} \cdot \frac{3}{2} = \frac{6}{6} = 1$

Porque su producto es$1$,$\frac{2}{3}$ y$\frac{3}{2}$ son recíprocos. Algunas otras reciprocas se enumeran a continuación:

$\frac{5}{8}\ \text{and}\ \frac{8}{5} \qquad 7\ \text{and}\ \frac{1}{7} \qquad -\frac{4}{5}\ \text{and}\ -\frac{5}{4}$

Esta definición es importante porque dividir fracciones requiere que multipliques el dividendo por el recíproco del divisor.

$\frac{a}{b} \div \color{Cerulean}{\frac{c}{d}} \color{Black}{=} \frac{a}{b} \cdot \color{Cerulean}{\frac{d}{c}} \color{Black}{=} \frac{ad}{bc} $

Ejemplo$\PageIndex{9}$

Dividir:$\frac{2}{3} \div \frac{5}{7}$

Solución

Multiplicar$\frac{2}{3}$ por el recíproco de$\frac{5}{7}$.

\ [
\ begin {align*}
\ frac {2} {3}\ div\ frac {5} {7} &=\ frac {2} {3}\ cdot\ frac {7} {5}\
&=\ frac {2\ cdot 7} {3\ cdot 5}\\
&=\ frac {14} {15}
\ end {align*}
\]

Respuesta:

$\frac{14}{15$

También hay que estar al tanto de otras formas de notación que indiquen división:/y —. Por ejemplo,

$5/(1/2) = 5*(2/1)=(5/1)*(2/1)= 10/1=10$

$\frac{\frac{7}{8}}{\color{Cerulean}{\frac{2}{3}}} \color{Black}{=} \frac{7}{8} \div \color{Cerulean}{\frac{2}{3}} \color{Black}{=} \frac{7}{8} \cdot \color{Cerulean}{\frac{3}{2}} \color{Black}{=} \frac{21}{16}$

Este último es un ejemplo de una fracción compleja, que es una fracción cuyo numerador, denominador, o ambos son fracciones.

Nota

Los estudiantes suelen preguntar por qué dividir equivale a multiplicar por el recíproco del divisor. Una explicación matemática viene del hecho de que el producto de los recíprocos es$1$. Si aplicamos la propiedad de identidad multiplicativa y multiplicamos el numerador y el denominador por el recíproco del denominador, entonces obtenemos lo siguiente:

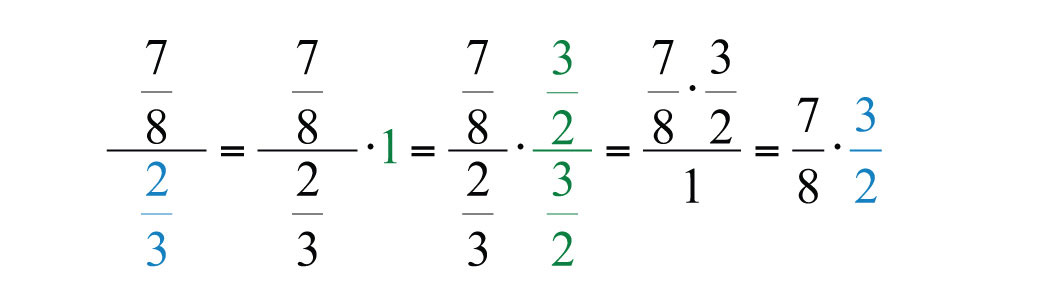
https://2012books.lardbucket.org/books/beginning-algebra/section_04/8ebd94dd18ea635671bfb0c1e1815b97.jpg — Figura$\PageIndex{11}$

Antes de multiplicarse, busque factores comunes para cancelar; esto elimina la necesidad de reducir el resultado final.

Ejemplo$\PageIndex{10}$

Dividir:$\frac{\frac{5}{2}}{\frac{7}{4}}$.

Solución

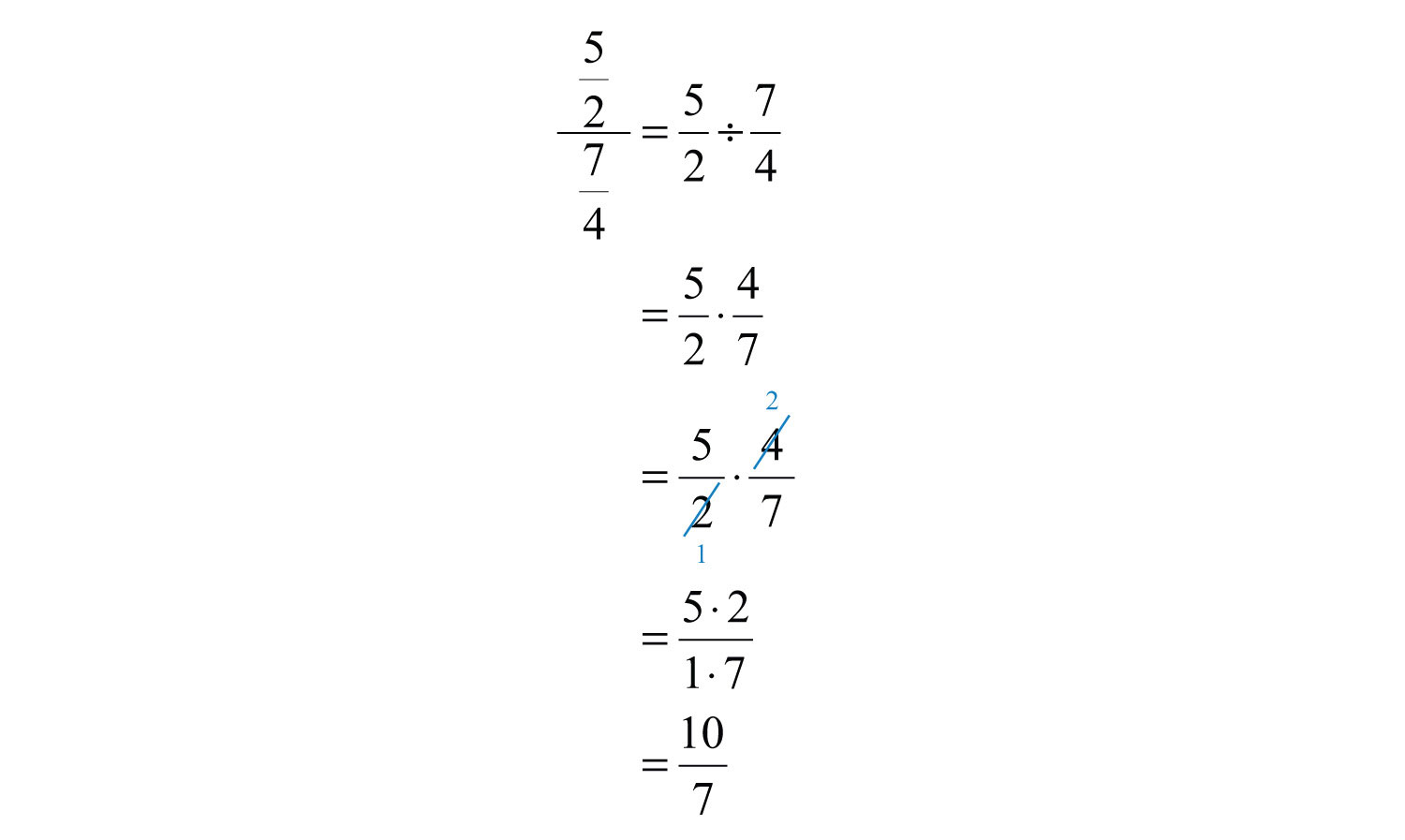
https://2012books.lardbucket.org/books/beginning-algebra/section_04/d4c0ce97216931d1e014dc4c8192fc38.jpg — Figura$\PageIndex{12}$

Responder

$\frac{10}{7}$

Al dividir por un entero, es útil reescribirlo como una fracción sobre$1$.

Ejemplo$\PageIndex{11}$

Dividir:$\frac{2}{3} \div 6$

Solución

Reescribe 6 como$\frac{6}{1}$ y multiplica por su recíproco.

https://2012books.lardbucket.org/books/beginning-algebra/section_04/da1f8518bd563a80c0a1a7bba6ec7a48.jpg — Figura$\PageIndex{13}$

Respuesta:

$\frac{1}{9}$

Además, tenga en cuenta que solo cancelamos cuando se trabaja con multiplicación. Reescribe cualquier problema de división como producto antes de cancelar.

Ejemplo$\PageIndex{12}$

¡Prueba esto! Dividir:$5 \div 2 \frac{3}{5} $

Solución de video:

(haga clic para ver el video)

Sumando y restando fracciones

Las fracciones negativas se indican con el signo negativo frente a la barra de fracciones, en el numerador o en el denominador. Todas esas formas son equivalentes e intercambiables.

$\frac{-3}{4} = -\frac{3}{4} = \frac{3}{-4}$

Sumar o restar fracciones requiere un denominador común. En esta sección, supongamos que el denominador común c es un entero distinto de cero.

Es una buena práctica utilizar denominadores comunes positivos expresando fracciones negativas con numeradores negativos. En definitiva, evitar denominadores negativos.

Ejemplo$\PageIndex{13}$

Restar:$\frac{12}{15} - \frac{3}{15}$

Solución

Las dos fracciones tienen un denominador común$15$. Por lo tanto, resta los numeradores y escribe el resultado sobre el denominador común:

\ [
\ begin {align*}
\ frac {12} {15} -\ frac {3} {15} &=\ frac {12-3} {15} &&\ color {cerúleo} {Restar\ los\ numeradores.} \\
&=\ color {Negro} {\ frac {9} {15}}\\
&=\ frac {9\ color {cerúleo} {\ div 3}} {\ color {Negro} {15}\ color {cerúleo} {\ div 3}} &&\ color {cerúleo} {Reducir.} \\
&=\ frac {3} {5}
\ final {alinear*}
\]

Responder
$\frac{3}{5}$

La mayoría de los problemas que es probable que encuentres tendrán denominadores diferentes. En este caso, primero encuentra fracciones equivalentes con un denominador común antes de sumar o restar los numeradores. Una forma de obtener fracciones equivalentes es dividir el numerador y el denominador por el mismo número. Ahora revisamos una técnica para encontrar fracciones equivalentes multiplicando el numerador y el denominador por el mismo número. Debe quedar claro que$5/5$ es igual a$1$ y que$1$ multiplicado por cualquier número es ese número:

$\frac{1}{2} = \frac{1}{2} \cdot \color{Cerulean}{1} \color{Black}{=} \frac{1}{2} \cdot \color{Cerulean}{\frac{5}{5}} \color{Black}{=} \frac{5}{10}$

Tenemos fracciones equivalentes$\frac{1}{2}=\frac{5}{10}$. Usa esta idea para encontrar fracciones equivalentes con un denominador común para sumar o restar fracciones. Los pasos se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{14}$

Restar:$\frac{7}{15} - \frac{3}{10}$

Solución

Paso 1: Determinar un denominador común. Para ello, utilice el múltiplo menos común (LCM) de los denominadores dados. El LCM de$15$ y$10$ está indicado por LCM$(15, 10)$. Trate de pensar en el número más pequeño en el que ambos denominadores dividen de manera uniforme. Enumere los múltiplos de cada número:

$https://2012books.lardbucket.org/books/beginning-algebra/section_04/ddcc1fb9e9d8cde747c45cb04d6386b1.jpg$

Los múltiplos comunes se enumeran en negrita, y el múltiplo menos común es$30$.

LCM$(10,15)=30$

Paso 2: Multiplica el numerador y el denominador de cada fracción por valores que dan como resultado fracciones equivalentes con el denominador común determinado.

\ [\ begin {align*}
\ frac {7} {15} -\ frac {3} {10} &=\ frac {7\ color {cerúleo} {\ cdot 2}} {15\ color {cerúleo} {\ cdot 3}} -\ frac {3\ color {cerúleo} {\ cdot 3}} {10\ color {cerúleo}\ cdot 3}}\\
&=\ frac {14} {30} -\ frac {9} {30}
\ final {alinear*}\]

Paso 3: Suma o resta los numeradores, escribe el resultado sobre el denominador común y luego reduce si es posible.

\ [\ begin {align*}
\ frac {14} {30} -\ frac {9} {30} &=\ frac {14-9} {30}\\
&=\ frac {5} {30}\\
&=\ frac {5\ color {cerúleo} {\ div 5}} {30\ color {cerúleo} {\ div 5}}\
&= frac {1} {6}
\ end {align*}\]

Respuesta:

$\frac{1}{6}$

El mínimo común múltiplo de los denominadores se llama el mínimo común denominador (LCD). Encontrar la pantalla LCD suele ser el paso difícil. Vale la pena encontrarlo porque si se usa algún múltiplo común que no sea el menor, entonces habrá más pasos involucrados a la hora de reducir.

Ejemplo$\PageIndex{15}$

Agregar:$\frac{5}{10} + \frac{1}{18}$

Solución

Primero, determinar que el LCM$(10, 18)$ es$90$ y luego encontrar fracciones equivalentes con$90$ como denominador.

\ [\ begin {align*}
\ frac {5} {10} +\ frac {1} {18} &=\ frac {5\ color {cerúleo} {\ cdot 9}} {10\ color {cerúleo} {\ cdot 9}} +\ frac {1\ color {cerúleo} {\ cdot 5}} {18\ color {cerúleo}\ cdot 5}}\\
&=\ frac {45} {90} +\ frac {5} {90}\\
&=\ frac {45+5} {90}\\
& amp; =\ frac {50} {90}\\
&=\ frac {50\ color {cerúleo} {\ div 10}} {90\ color {cerúleo} {\ div 10}}\\
&=\ frac {5} {9}
\ end {align*}\]

Responder

$\frac{5}{9}$

Ejemplo$\PageIndex{16}$

¡Prueba esto! Agregar:$\frac{2}{30} + \frac{5}{21}$

Solución de video:

(haga clic para ver el video)

Ejemplo$\PageIndex{17}$

Simplificar:$2 \frac{1}{3} + \frac{3}{5} - \frac{1}{2}$

Solución

Comience por convertir$2 \frac{1}{3}$ a una fracción impropia.

$clipboard_e7e9738610c56f1a7c329f3819ae3778f.png$

Respuesta:

$2 \frac{13}{30}$

En general, es preferible trabajar con fracciones inadecuadas. No obstante, cuando el problema original involucra números mixtos, si procede, presenta tus respuestas como números mixtos. Además, a menudo se prefieren los números mixtos cuando se trabaja con números en una línea numérica y con aplicaciones del mundo real.

Ejemplo$\PageIndex{18}$

¡Prueba esto! Restar:$\frac{5}{7} - 2 \frac{1}{7}$

Solución de video:

(haga clic para ver el video)

Ejemplo$\PageIndex{19}$

¿Cuántos libros de bolsillo de$\frac{1}{2}$ pulgadas de grosor se pueden apilar para que quepan en una repisa que tiene$1 \frac{1}{2}$ pies de altura?

Solución

Primero, determinar la altura de la repisa en pulgadas. Para ello, usa el hecho de que hay$12$ pulgadas en$1$ pie y multiplica de la siguiente manera:

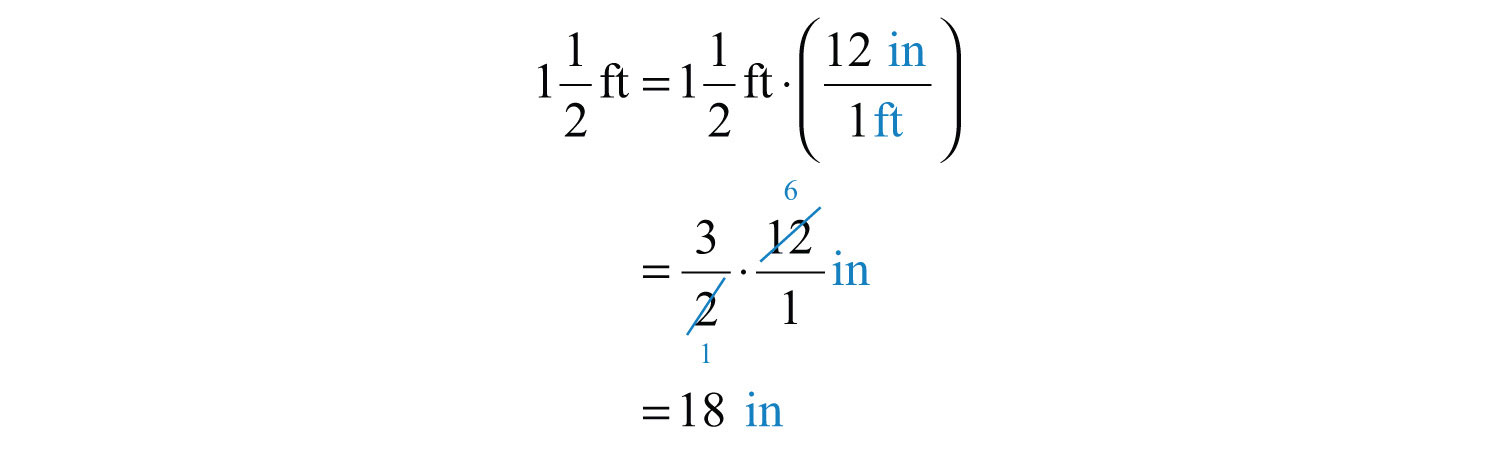
$clipboard_ed64be26f369e37959027b418e41aa38b.png$

A continuación, determine cuántos cuadernos cabrán dividiendo la altura de la repisa por el grosor de cada libro.

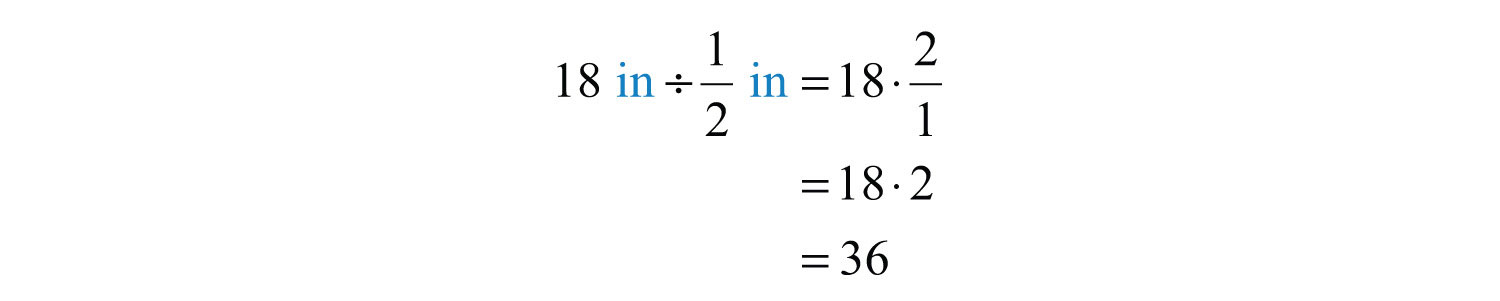
$clipboard_e628fb6f31ac27f7376e007050de71417.png$

Responder

$36$los libros se pueden apilar en la repisa.

Puntos clave:

Las fracciones no son únicas; hay muchas formas de expresar la misma proporción. Encuentra fracciones equivalentes multiplicando o dividiendo el numerador y el denominador por el mismo número real.
Generalmente se prefieren las fracciones equivalentes en términos más bajos. Es una buena práctica reducir siempre.
En álgebra, generalmente se prefieren las fracciones impropias. Sin embargo, en aplicaciones de la vida real, a menudo se prefieren los equivalentes de números mixtos. Podemos presentar las respuestas como fracciones impropias a menos que la pregunta original contenga números mixtos, o sea una respuesta a una aplicación del mundo real o geométrica.
Multiplicar fracciones no requiere un denominador común; multiplicar los numeradores y multiplicar los denominadores para obtener el producto. Es una buena práctica cancelar cualquier factor común en el numerador y el denominador antes de multiplicarse.
Los recíprocos son números racionales cuyo producto es igual a$1$. Dada una fracción$\frac{a}{b}$, su recíproco es$\frac{b}{a}$.
Dividir fracciones multiplicando el dividendo por el recíproco del divisor. Es decir, multiplicar el numerador por el recíproco del denominador.
Reescribe cualquier problema de división como producto antes de cancelar.
Sumar o restar fracciones requiere un denominador común. Cuando los denominadores de cualquier número de fracciones son iguales, simplemente suma o resta los numeradores y escribe el resultado sobre el denominador común.
Antes de sumar o restar fracciones, asegúrese de que los denominadores sean los mismos encontrando fracciones equivalentes con un denominador común. Multiplique el numerador y el denominador de cada fracción por el valor apropiado para encontrar las fracciones equivalentes.
Por lo general, es mejor convertir todos los números mixtos en fracciones impropias antes de comenzar el proceso de sumar, restar, multiplicar o dividir.

Ejercicio$\PageIndex{1}$

Reduzca cada fracción a los términos más bajos.

1. $\frac{5}{30}$

2. $\frac{6}{24}$

3. $\frac{30}{70}$

4. $\frac{18}{27}$

5. $\frac{44}{84}$

6. $\frac{54}{90}$

7. $\frac{135}{30}$

8. $\frac{105}{300}$

9. $\frac{18}{6}$

10. $\frac{256}{16}$

11. $\frac{126}{45}$

12. $\frac{52}{234}$

13. $\frac{54}{162}$

14. $\frac{2000}{3000}$

15. $\frac{270}{360}$

Responder

1:$1/6$

3:$3/7$

5:$11/21$

7:$9/2$

9:$3$

11:$14/5$

13:$1/3$

15:$3/4$

Ejercicio$\PageIndex{2}$

Reescribir como una fracción impropia.

$4\frac{3}{4}$
$2\frac{1}{2}$
$5\frac{7}{15}$
$1\frac{1}{2}$
$3\frac{5}{8}$
$1\frac{3}{4}$
$−2\frac{1}{2}$
$−1\frac{3}{4}$

Responder

1:$5/2$

3:$3/2$

5:$7/4$

7:$−7/4$

Ejercicio$\PageIndex{3}$

Reescribir como un número mixto.

$\frac{15}{2}$
$\frac{9}{2}$
$\frac{40}{13}$
$\frac{103}{25}$
$\frac{73}{10}$
$\frac{−52}{7}$
$\frac{−59}{6}$

Responder

2:$4\frac{1}{2}$

4:$4\frac{3}{25}$

6:$−7\frac{3}{7}$

Ejercicio$\PageIndex{4}$

Multiplicar y reducir a los términos más bajos.

$\frac{2}{3}⋅\frac{5}{7}$
$\frac{1}{5}⋅\frac{4}{8}$
$\frac{1}{2}⋅\frac{1}{3}$
$\frac{3}{4}⋅\frac{20}{9}$
$\frac{5}{7}⋅\frac{49}{10}$
$\frac{2}{3}⋅\frac{9}{12}$
$\frac{6}{14}⋅\frac{21}{12}$
$\frac{44}{15}⋅\frac{15}{11}$
$3 \frac{3}{4} \cdot 2 \frac{1}{3}$
$2\frac{7}{10}⋅5\frac{5}{6}$
$\frac{3}{11}(−\frac{5}{2})$
$-\frac{4}{5}(\frac{9}{5})$
$(−\frac{9}{5} (−\frac{3}{10}) $
$\frac{6}{7}(−\frac{14}{3})$
$(−\frac{9}{12})(−\frac{4}{8})$
$−\frac{3}{8}(−\frac{4}{15})$
$\frac{1}{7}⋅\frac{1}{2}⋅\frac{1}{3}$
$\frac{3}{5}⋅\frac{15}{21}⋅\frac{7}{27}$
$\frac{2}{5}⋅3\frac{1}{8}⋅\frac{4}{5}$
$2\frac{4}{9}⋅\frac{2}{5}⋅2\frac{5}{11}$

Responder

1:$10/21$

3:$1/6$

5:$7/2$

7:$3/4$

9:$834$

11:$−15/22$

13:$27/50$

15:$3/8$

17:$1/42$

19:$1$

Ejercicio$\PageIndex{5}$

Determinar el recíproco de los siguientes números.

$\frac{1}{2}$
$\frac{8}{5}$
$−\frac{2}{3}$
$−\frac{4}{3}$
$10$
$−4$
$2\frac{1}{3}$
$1\frac{5}{8}$

Responder

1:$2$

3:$−3/2$

5:$1/10$

7:$3/7$

9:$3/4$

Ejercicio$\PageIndex{6}$

Dividir y reducir a los términos más bajos.

$\frac{1}{2} \div \frac{2}{3}$
$\frac{5}{9} \div \frac{1}{3}$
$\frac{5}{8} \div (−\frac{4}{5})$
$(−\frac{2}{5})÷\frac{15}{3}$
$\dfrac{−\frac{6}{7}}{−\frac{6}{7}}$
$\dfrac{−\frac{1}{2}}{\frac{1}{4}}$
$\dfrac{−\frac{10}{3}}{−\frac{5}{20}}$
$\dfrac{\frac{2}{3}}{\frac{9}{2}}$
$\dfrac{\frac{30}{50}}{\frac{5}{3}}$
$\dfrac{\frac{1}{2}}{2}$
$\dfrac{5}{\frac{2}{5}}$
$\dfrac{−6}{\frac{5}{4}}$
$2 \frac{1}{2} \div \frac{5}{3}$
$4 \frac{2}{3} \div 3 \frac{1}{2}$
$5 \div 2\frac{3}{5}$
$4\frac{3}{5} \div 23$

Responder

1:$3/4$

3:$−25/32$

5:$1$

7:$40/3$

9:$9/25$

11:$25/2$

13:$1 \frac{1}{2}$

15:$1 \frac{12}{13}$

Ejercicio$\PageIndex{7}$

Sumar o restar y reducir a los términos más bajos.

$\frac{17}{20}-\frac{5}{20}$
$\frac{4}{9}-\frac{13}{9}$
$\frac{3}{5}+\frac{1}{5}$
$\frac{11}{15}+\frac{9}{15}$
$\frac{5}{7}-2\frac{1}{7}$
$\frac{1}{2}+\frac{1}{3}$
$\frac{1}{5}-\frac{1}{4}$
$\frac{3}{4}-\frac{5}{2}$
$\frac{3}{8}+\frac{7}{16}$
$\frac{7}{15}-\frac{3}{10}$
$\frac{3}{10}+\frac{2}{14}$
$\frac{2}{30}+\frac{5}{21}$
$\frac{3}{18}-\frac{1}{24}$
$5 \frac{1}{2}+2\frac{1}{3}$
$1 \frac{3}{4}+2 \frac{1}{10}$
$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$
$\frac{2}{3}+\frac{3}{5}-\frac{2}{9}$
$\frac{7}{3}-\frac{3}{2}+\frac{2}{15}$
$\frac{9}{4}-\frac{3}{2}+\frac{3}{8}$
$\frac{2}{3}-4\frac{1}{2}+3\frac{1}{6}$
$1-\frac{6}{16}+\frac{3}{18}$
$3-\frac{1}{21}-\frac{1}{15}$

Responder

1:$3/5$

3:$4/5$

5:$−1 \frac{3}{7}$

7:$5/6$

9:$−7/4$

11:$1/6$

13:$32/105$

15:$7 \frac{5}{6}$

17:$1$

19:$29/30$

21:$2 \frac{2}{3}$

23:$19/24$

Ejercicio$\PageIndex{8}$

Realizar las operaciones. Reducir las respuestas a los términos más bajos.

$\frac{3}{14} \cdot \frac{7}{3} \div \frac{1}{8}$
$\frac{1}{2} \cdot (-\frac{4}{5}) \div \frac{14}{15}$
$\frac{1}{2} \div \frac{3}{4} \cdot \frac{1}{5}$
$-\frac{5}{9} \div \frac{5}{3} \cdot \frac{5}{2}$
$\frac{4}{5} \div 4 \cdot \frac{1}{2}$
$\frac{5}{3} \div 15 \cdot \frac{2}{3}$
¿Cuál es el producto de$\frac{3}{16}$ y$\frac{4}{9}$?
¿Cuál es el producto de$−\frac{24}{5}$ y$\frac{25}{8}$?
¿Cuál es el cociente de$\frac{5}{9}$ y$\frac{25}{3}$?
¿Cuál es el cociente de$−\frac{16}{5}$ y$32$?
Restar$\frac{1}{6}$ de la suma de$\frac{9}{2}$ y$\frac{2}{3}$.
Restar$\frac{1}{4}$ de la suma de$\frac{3}{4}$ y$\frac{6}{5}$.
¿Cuál es el ancho total cuando$3$ las tablas, cada una con un ancho de$2 \frac{5}{8}$ pulgadas, se pegan entre sí?
La precipitación en pulgadas para un fin de semana particular de 3 días se publicó como$\frac{3}{10}$ pulgadas el viernes,$1\frac{1}{2}$ pulgadas el sábado y$\frac{3}{4}$ pulgadas el domingo. Calcular la precipitación total a lo largo de este periodo.
Una tabla que mide$5\frac{1}{4}$ pies de largo se va a cortar en$7$ trozos de igual longitud. ¿Cuál es la longitud de cada pieza?
¿Cuántas cuadernos de$\frac{3}{4}$ pulgadas de grosor se pueden apilar en una caja de$2$ pies de altura?
En una clase de matemáticas de$44$ estudiantes, una cuarta parte de los estudiantes se inscribió en una sesión especial de estudio los sábados. ¿Cuántos alumnos se inscribieron?
Determinar la longitud de la esgrima necesaria para encerrar una pluma rectangular con dimensiones$35\frac{1}{2}$ pies a$20\frac{2}{3}$ pies.
Cada vuelta alrededor de la pista mide$\frac{1}{4}$ milla. ¿Cuántas vueltas se requieren para completar una carrera de una$2\frac{1}{2}$ milla?
Un jubilado obtuvo una pensión que consiste en las tres cuartas partes de su salario mensual regular. Si su salario mensual regular era$$5,200$, entonces ¿qué pago mensual puede esperar el jubilado del plan de pensiones?

Responder

1:$4$

3:$2/15$

5:$9/28$

7:$1/10$

9:$1/12$

11:$1/15$

13:$5$

15:$7 \frac{7}{8}$ pulgadas

17:$\frac{3}{4}$ pies

19:$11$ estudiantes

21:$10$ vueltas

Ejercicio$\PageIndex{1}$

Temas del tablero de discusión

¿$0$Tiene un recíproco? Explique.
Explicar la diferencia entre el MCM y el GCF. Dé un ejemplo.
Explique la diferencia entre el LCM y el LCD.
¿Por qué es necesario encontrar una LCD para sumar o restar fracciones?
Explicar cómo determinar qué fracción es mayor,$\frac{7}{16}$ o$\frac{1}{2}$.

Search

Text Color

Text Size

Margin Size

Font Type

Puntos clave: