5.4: Multiplicar polinomios

Última actualización
Guardar como PDF

Page ID: 110058

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Multiplicar un polinomio por un monomio.
Multiplicar un polinomio por un binomio.
Multiplica un polinomio por polinomio de cualquier tamaño.
Reconocer y calcular productos especiales.
Multiplicar funciones polinómicas.

Multiplicando por un Monomio

Recordemos la regla del producto para exponentes: si$m$ y$n$ son enteros positivos, entonces

\[x^{m}\cdot x^{n}=x^{m+n}\]

Es decir, al multiplicar dos expresiones con la misma base, sumar los exponentes. Esta regla se aplica cuando se multiplica un monomio por un monomio. Para encontrar el producto de los monomios, multiplique los coeficientes y sume los exponentes de factores variables con la misma base. Por ejemplo,

$\begin{array} {cl} {3x\cdot 5x^{2} = 3\cdot 5\cdot x^{1}\cdot x^{2}}&{\color{Cerulean}{Commutative\: property}}\\{=15x^{1+2}}&{\color{Cerulean}{Product\:rule\:for\:exponents}}\\{=15x^{3}}&{} \end{array}$

Para multiplicar un polinomio por un monomio, aplicar la propiedad distributiva y luego simplificar cada término.

Ejemplo$\PageIndex{1}$

Multiplicar:

$−5x(4x−2)$.

Solución:

En este caso, multiplicar el monomio,$−5x$, por el binomio,$4x−2$. Aplicar la propiedad distributiva y luego simplificar.

Captura de pantalla (365) .png — Figura$\PageIndex{1}$

Respuesta:

$-20x^{2}+10x$

Ejemplo$\PageIndex{2}$

Multiplicar:

$2x^{2}(3x^{2}−5x+1)$.

Solución:

Aplicar la propiedad distributiva y luego simplificar.

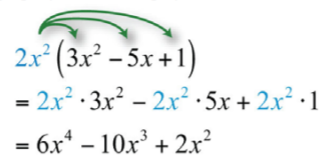Captura de pantalla (366) .png — Figura$\PageIndex{2}$

Respuesta:

$6x^{4}-10x^{3}+2x^{2}$

Ejemplo$\PageIndex{3}$

Multiplicar:

$−3ab^{2}(a^{2}b^{3}+2a^{3}b−6ab−4)$.

Solución:

Respuesta:

En resumen, multiplicar un polinomio por un monomio implica la propiedad distributiva y la regla del producto para los exponentes. Multiplicar todos los términos del polinomio por el monomio. Para cada término, multiplicar los coeficientes y sumar exponentes de variables donde las bases son las mismas.

Ejercicio$\PageIndex{1}$

Multiplicar:

$−5x^{2}y(2xy^{2}−3xy+6x^{2}y−1)$.

Contestar: $−10x^{3}y^{3}+15x^{3}y^{2}−30x^{4}y^{2}+5x^{2}y$

Multiplicar por un Binomio

De la misma manera que usamos la propiedad distributiva para encontrar el producto de un monomio y un binomio, lo usaremos para encontrar el producto de dos binomios.

\[\begin{aligned} \color{Cerulean}{(a+b)}\color{black}{(c+d)} \\ &=\color{Cerulean}{(a+b)}\color{black}{\cdot c+}\color{Cerulean}{(a+b)}\color{black}{\cdot d} \\ &=ac+bc+ad+bd \\ &=ac+ad+bc+bd \end{aligned}\]

Aquí aplicamos la propiedad distributiva varias veces para producir el resultado final. Este mismo resultado se obtiene en un solo paso si aplicamos la propiedad distributiva a$a$ y$b$ por separado de la siguiente manera:

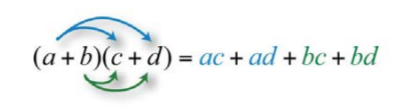Captura de pantalla (367) .png — Figura$\PageIndex{3}$

Esto a menudo se llama el método FOIL. Agregamos los productos de los primeros términos de cada binomio$ac$, los términos$o$ uter$ad$, los términos$i$$bc$ nner y finalmente los últimos términos$bd$. Este dispositivo mnemotécnico solo funciona para productos de binomios; de ahí que lo mejor sea recordar que se aplica la propiedad distributiva.

Ejemplo$\PageIndex{4}$

Multiplicar:

$(2x+3)(5x−2)$.

Solución:

Distribuir$2x$ y luego distribuir$3$.

Simplifica combinando términos similares.

$=10x^{2}+11x-6$

Respuesta:

$10x^{2}+11x-6$

Ejemplo$\PageIndex{5}$

Multiplicar:

$(\frac{1}{2}x−\frac{1}{4})(\frac{1}{2}x+\frac{1}{4})$.

Solución:

Distribuir$\frac{1}{2}x$ y luego distribuir$−\frac{1}{4}$.

$\begin{aligned} (\frac{1}{2}x−\frac{1}{4})(\frac{1}{2}x+\frac{1}{4}) &=\color{Cerulean}{\frac{1}{2}x}\color{black}{\frac{1}{2}x+}\color{Cerulean}{\frac{1}{2}x}\color{black}{\cdot\frac{1}{4}+}\color{OliveGreen}{\left( -\frac{1}{4} \right)}\color{black}{\cdot\frac{1}{2}x+}\color{OliveGreen}{\left(-\frac{1}{4} \right)}\color{black}{\cdot\frac{1}{4}} \\ &=\frac{1}{4}x^{2}+\frac{1}{8}x-\frac{1}{8}x-\frac{1}{16} \\ &=\frac{1}{4}x^{2}-\frac{1}{16} \end{aligned}$

Respuesta:

$\frac{1}{4}x^{2}-\frac{1}{16}$

Ejemplo$\PageIndex{6}$

Multiplicar:

$(3y^{2}−1)(2y+1)$.

Solución:

Respuesta:

$6y^{3}+3y^{2}-2y-1$

Después de aplicar la propiedad distributiva, combine cualquier término similar.

Ejemplo$\PageIndex{7}$

Multiplicar:

$(x^{2}−5)(3x^{2}−2x+2)$.

Solución:

Después de multiplicar cada término del trinomio por$x^{2}$ y$−5$, simplificar.

Respuesta:

$3x^{4}-2x^{3}-13x^{2}+10x-10$

Ejemplo$\PageIndex{8}$

Multiplicar:

$(2x−1)^{3}$.

Solución:

Realizar un producto a la vez.

Captura de pantalla (368) .png — Figura$\PageIndex{4}$

Respuesta:

$8x^{3}-12x^{2}+6x-1$

En este punto, vale la pena señalar un error común:

$(2x-1)^{3}\neq (2x)^{3}-(1)^{3}$

La confusión viene del producto a una regla de poder de exponentes, donde aplicamos el poder a todos los factores. Dado que hay dos términos dentro de los paréntesis, esa regla no aplica. Se debe tener cuidado para entender lo que es diferente en los siguientes dos ejemplos:

$\begin{aligned} (xy)^{2} &=x^{2}y^{2}\quad\color{Cerulean}{\checkmark} \\ (x+y)^{2} &\neq x^{2}+y^{2}\quad\color{red}{x} \end{aligned}$

Ejercicio$\PageIndex{2}$

Multiplicar:

$(2x−3)(7x^{2}−5x+4)$.

Contestar: $14x^{3}-31x^{2}+23x-12$

Producto de polinomios

Al multiplicar polinomios, aplicamos la propiedad distributiva muchas veces. Multiplica todos los términos de cada polinomio y luego combina términos similares.

Ejemplo$\PageIndex{9}$

Multiplicar:

$(2x^{2}+x−3)(x^{2}−2x+5)$.

Solución:

Multiplicar cada término del primer trinomio por cada término del segundo trinomio y luego combinar términos similares.

Alinear términos similares en columnas, como tenemos aquí, ayuda en el proceso de simplificación

Respuesta:

$2x^{4}-3x^{3}+5x^{2}+11x-15$

Observe que al multiplicar un trinomio por un trinomio, obtenemos nueve términos antes de simplificarlo. De hecho, al multiplicar un polinomio$n$ -term por un polinomio m-term, obtendremos$n × m$ términos. En el ejemplo anterior, se nos pidió multiplicar y encontramos que

$(2x^{2}+x-3)(x^{2}-2x+5)=2x^{4}-3x^{3}+5x^{2}+11x-15$

Debido a que es fácil hacer un pequeño error de cálculo, es una buena práctica rastrear mentalmente los pasos para verificar que las operaciones se realizaron correctamente. Alternativamente, podemos verificar evaluando cualquier valor para$x$ en ambas expresiones para verificar que los resultados son los mismos. Aquí elegimos$x = 2$:

$\begin{aligned} (2x^{2}+x-3)(x^{2}-2x+5)&=(2(\color{OliveGreen}{2}\color{black}{)^{2}+(}\color{OliveGreen}{2}\color{black}{)-3)((}\color{OliveGreen}{2}\color{black}{)^{2}-2(}\color{OliveGreen}{2}\color{black}{)+5)} \\ &=(8+2-3)(4-4+5) \\ &=(7)(5) \\ &=35 \end{aligned}$

Debido a que los resultados podrían ser coincidentemente los mismos, un cheque evaluando no necesariamente prueba que nos hemos multiplicado correctamente. Sin embargo, después de verificar algunos valores, podemos estar bastante seguros de que el producto es correcto.

Ejercicio$\PageIndex{3}$

Multiplicar:

$(x^{2}−2x−3)^{2}$.

Contestar: $x^{4}−4x^{3}−2x^{2}+12x+9$

Productos Especiales

En esta sección, el objetivo es reconocer ciertos productos especiales que ocurren a menudo en nuestro estudio del álgebra. Desarrollaremos tres fórmulas que serán muy útiles a medida que avancemos. Los tres deben ser memorizados. Comenzamos considerando los siguientes dos cálculos:

$\begin{array}{r|r} {(a+b)^{2}=(a+b)(a+b)}&{(a-b)^{2}=(a-b)(a-b)}\\{=a^{2}+ab+ba+b^{2}}&{=a^{2}-ab-ba+b^{2}}\\{=a^{2}+ab+ab+b^{2}}&{=a^{2}-ab-ab+b^{2}}\\{=a^{2}+2ab+b^{2}}&{=a^{2}-2ab+b^{2}} \end{array}$

Esto nos lleva a dos fórmulas que describen trinomios cuadrados perfectos:

\[ (a+b)^{2}=a^{2}+2ab+b^{2} \]

\[ (a-b)^{2}=a^{2}-2ab+b^{2}\]

Podemos usar estas fórmulas para cuadrar rápidamente un binomio.

Ejemplo$\PageIndex{10}$

Multiplicar:

$(3x+5)^{2}$.

Solución:

Aquí$a=3x$ y$b=5$. Aplicar la fórmula:

$\begin{aligned} \color{Cerulean}{(a+b)^{2}} &\color{Cerulean}{ =\:\: a^{2}\:\:\:\:+2\:\:\:\:\:\:a\:\:\:\:\:b\:\:+\:\:b^{2}} \\ &\color{Cerulean}{\quad\:\:\: \downarrow\qquad\qquad\:\: \downarrow\:\:\:\:\: \downarrow\qquad\downarrow} \\ (3x+5)^{2}&=(3x)^{2}+2\cdot(3x)(5)+(5)^{2} \\ &=9x^{2}+30x+25\end{aligned}$

Respuesta:

$9x^{2}+30x+25$

Este proceso debe llegar a ser lo suficientemente rutinario como para ser realizado mentalmente.

Ejemplo$\PageIndex{11}$

Multiplicar:

$(x−4)^{2}$.

Solución:

Aquí$a=x$ y$b=4$. Aplicar la fórmula apropiada de la siguiente manera:

$\begin{aligned} \color{Cerulean}{(a-b)^{2}} &\color{Cerulean}{ =\:\: a^{2}\:\:\:\:-2\:\:\:\:a\:\:\:b\:\:+\:b^{2}} \\ &\color{Cerulean}{\quad\:\:\: \downarrow\qquad\quad\:\:\:\: \downarrow\:\:\: \downarrow\quad\:\:\:\downarrow} \\ (x-4)^{2}&=(x)^{2}-2\cdot(x)(4)+(4)^{2} \\ &=x^{2}-8x+16\end{aligned}$

Respuesta:

$x^{2}-8x+16$

Nuestro tercer producto especial sigue:

$\begin{aligned}(a+b)(a-b)&=a^{2}-ab+ba-b^{2} \\ &=a^{2}\color{red}{-ab+ab}\color{black}{-b^{2}}\\&=a^{2}-b^{2} \end{aligned}$

Este producto se llama diferencia de cuadrados:

\[(a+b)(a-b)=a^{2}-b^{2}\]

Los binomios$(a+b)$ y$(a−b)$ se denominan binomios conjugados. Por lo tanto, cuando se multiplican los binomios conjugados, el término medio elimina, y el producto es en sí mismo un binomio.

Ejemplo$\PageIndex{12}$

Multiplicar:

$(7x+4)(7x−4)$.

Solución:

Respuesta:

$49x^{2}-16$

Ejercicio$\PageIndex{4}$

Multiplicar:

$(−5x+2)^{2}$.

Contestar: $25x^{2}−20x+4$

Multiplicar funciones polinomiales

Usamos la notación de funciones para indicar la multiplicación de la siguiente manera:

Mesa$\PageIndex{1}$
Multiplicación de funciones:	$(f\cdot g)(x)=f(x)\cdot g(x)$

Ejemplo$\PageIndex{13}$

Calcular:

$(f⋅g)(x)$, dado$f(x)=5x^{2}$ y$g(x)=−x^{2}+2x−3$.

Solución:

Multiplicar todos los términos del trinomio por la función monomial$f(x)$.

$\begin{aligned} (f\cdot g)(x)&=f(x)\cdot g(x) \\ &=5x^{2}\cdot (-x^{2}+2x-3) \\ &=-5x^{4}+10x^{3}-15x^{2} \end{aligned}$

Respuesta:

$(f\cdot g)(x)=-5x^{4}+10x^{3}-15x^{2}$

Ejemplo$\PageIndex{14}$

Calcular:

$(f⋅g)(−1)$, dado$f(x)=−x+3$ y$g(x)=4x^{2}−3x+6$.

Solución:

Primero, determinar$(f⋅g)(x)$.

$\begin{aligned} (f\cdot g)(x) &=f(x)\cdot g(x) \\ &=(-x+3)(4x^{2}-3x+6) \\ &=-4x^{3}+3x^{2}-6x+12x^{2}-9x+18 \\ &=-4x^{3}+15x^{2}-15x+18 \end{aligned}$

Tenemos

\ ((f\ cdot g) (x) = -4x^ {3} +15x^ {2} -15x+18

A continuación, sustituya$−1$ la variable$x$.

$\begin{aligned} (f\cdot g)(\color{OliveGreen}{-1}\color{black}{)}&=-4(\color{OliveGreen}{-1}\color{black}{)^{3}+15(}\color{OliveGreen}{-1}\color{black}{)^{2}-15(}\color{OliveGreen}{-1}\color{black}{)+18} \\ &=-4\cdot (-1)+15\cdot 1+15+18 \\ &=4+15+15+18 \\ &=52 \end{aligned}$

Respuesta:

$(f\cdot g)(-1)=52$

Porque$(f⋅g)(−1)=f(−1)⋅g(−1)$, alternativamente podríamos calcular$f(−1)$ y$g(−1)$ por separado y luego multiplicar los resultados (probar esto como un ejercicio). Sin embargo, si nos pidieran evaluar múltiples valores para la función$(f⋅g)(x)$, lo mejor sería determinar primero la forma general, como tenemos en el ejemplo anterior.

Claves para llevar

Para multiplicar un polinomio por un monomio, aplicar la propiedad distributiva y luego simplificar cada uno de los términos resultantes.
Para multiplicar polinomios, multiplica cada término en el primer polinomio con cada término en el segundo polinomio. Después combina términos similares.
El producto de un polinomio de$n$ término y un polinomio de$m$ término da como resultado un polinomio de$m × n$ término antes de combinar términos similares.
Verifique los resultados evaluando valores en la expresión original y en su respuesta para verificar que los resultados son los mismos.
Utilice las fórmulas para productos especiales para multiplicar rápidamente binomios que ocurren a menudo en álgebra.

Ejercicio$\PageIndex{5}$ Product of a Monomial and a Polynomial

Multiplicar.

$5x(−3x^{2}y)$
$(−2x^{3}y^{2})(−3xy^{4})$
$\frac{1}{2}(4x−3)$
$−\frac{3}{4}(\frac{2}{3}x−6)$
$3x(5x−2)$
$−4x(2x−1)$
$x^{2}(3x+2)$
$−6x^{2}(5x+3)$
$2ab(4a−2b)$
$5a^{2}b(a^{2}−b^{2})$
$6x^{2}y^{3}(−3x^{3}y+xy^{2})$
$3ab^{3}(−5ab^{3}+6a^{2}b)$
$−\frac{1}{2}x^{2}y(4xy−10)$
$−3x^{4}y^{2}(3x^{8}y^{3})$
$2x^{2}(−5x^{3})(3x^{4})$
$4ab(a^{2}b^{3}c)(a^{4}b^{2}c^{4})$
$−2(5x^{2}−3x+4)$
$\frac{4}{5}(25x^{2}−50xy+5y^{2})$
$3x(5x^{2}−2x+3)$
$−x(x^{2}+x−1)$
$x^{2}(3x^{2}−5x−7)$
$x^{3}(−4x^{2}−7x+9)$
$\frac{1}{4}x^{4}(8x^{3}−2x^{2}+\frac{1}{2}x−5)$
$−\frac{1}{3}x^{3}(\frac{3}{2}x^{5}−\frac{2}{3}x^{3}+\frac{9}{2}x−1)$
$a^{2}b(a^{2}−3ab+b^{2})$
$6a^{2}bc^{3}(2a−3b+c^{2})$
$\frac{2}{3}xy^{2}(9x^{3}y−27xy+3xy^{3})$
$−3x^{2}y^{2}(12x^{2}−10xy−6y^{2})$
Encuentra el producto de$3x$ y$2x^{2}−3x+5$.
Encuentra el producto de$−8y$ y$y^{2}−2y+12$.
Encuentra el producto de$−4x$ y$x^{4}−3x^{3}+2x^{2}−7x+8$.
Encuentra el producto de$3xy^{2}$ y$−2x^{2}y+4xy−xy^{2}$.

Contestar

1. $−15x^{3}y$

3. $2x−\frac{3}{2}$

5. $15x^{2}−6x$

7. $3x^{3}+2x^{2}$

9. $8a^{2}b−4ab^{2}$

11. $−18x^{5}y^{4}+6x^{3}y^{5}$

13. $−2x^{3}y^{2}+5x^{2}y$

15. $−30x^{9}$

17. $−10x^{2}+6x−8$

19. $15x^{3}−6x^{2}+9x$

21. $3x^{4}−5x^{3}−7x^{2}$

23. $2x^{7}−\frac{1}{2}x^{6}+\frac{1}{8}x^{5}−\frac{5}{4}x^{4}$

25. $a^{4}b−3a^{3}b^{2}+a^{2}b^{3}$

27. $6x^{4}y^{3}−18x^{2}y^{3}+2x^{2}y^{5}$

29. $6x^{3}−9x^{2}+15x$

31. $−4x^{5}+12x^{4}−8x^{3}+28x^{2}−32x$

Ejercicio$\PageIndex{6}$ Product of a Binomial and a Polynomial

Multiplicar.

$(3x−2)(x+4) $
$(x+2)(x−3) $
$(x−1)(x+1) $
$(3x−1)(3x+1) $
$(2x−5)(x+3) $
$(5x−2)(3x+4) $
$(−3x+1)(x−1) $
$(x+5)(−x+1) $
$(y−\frac{2}{3})(y+\frac{2}{3})$
$(\frac{1}{2}x+\frac{1}{3})(\frac{3}{2}x−\frac{2}{3})$
$(\frac{3}{4}x+\frac{1}{5})(\frac{1}{4}x+\frac{2}{5})$
$(\frac{1}{5}x+\frac{3}{10})(\frac{3}{5}x−\frac{5}{2})$
$(y^{2}−2)(y+2)$
$(y^{3}−1)(y^{2}+2)$
$(a^{2}−b^{2})(a^{2}+b^{2})$
$(a^{2}−3b)^{2}$
$(x−5)(2x^{2}+3x+4) $
$(3x−1)(x^{2}−4x+7) $
$(2x−3)(4x^{2}+6x+9) $
$(5x+1)(25x^{2}−5x+1) $
$(x−\frac{1}{2})(3x^{2}+4x−1) $
$(\frac{1}{3}x−\frac{1}{4})(3x^{2}+9x−3) $
$(x+3)^{3}$
$(x−2)^{3}$
$(3x−1)^{3}$
$(2x+y)^{3}$
$(5x−2)(2x^{3}−4x^{2}+3x−2)$
$(x^{2}−2)(x^{3}−2x^{2}+x+1)$

Contestar

1. $3x^{2}+10x−8 $

3. $x^{2}−1 $

5. $2x^{2}+x−15 $

7. $−3x^{2}+4x−1 $

9. $y^{2}−\frac{4}{9}$

11. $\frac{3}{16}x^{2}+\frac{7}{20}x+\frac{2}{25}$

13. $y^{3}+2y^{2}−2y−4$

15. $a^{4}−b^{4}$

17. $2x^{3}−7x^{2}−11x−20 $

19. $8x^{3}−27 $

21. $3x^{3}+\frac{5}{2}x^{2}−3x+12$

23. $x^{3}+9x^{2}+27x+27$

25. $27x^{3}−27x^{2}+9x−1 $

27. $10x^{4}−24x^{3}+23x^{2}−16x+4$

Ejercicio$\PageIndex{7}$ Product of Polynomials

Multiplicar.

$(x^{2}−x+1)(x^{2}+2x+1)$
$(3x^{2}−2x−1)(2x^{2}+3x−4)$
$(2x^{2}−3x+5)(x^{2}+5x−1)$
$(a+b+c)(a−b−c)$
$(a+2b−c)^{2}$
$(x+y+z)^{2}$
$(x−3)^{4}$
$(x+y)^{4}$
Encuentra el volumen de un sólido rectangular con lados de medición$x, x+2$, y$x+4$ unidades.
Encuentra el volumen de un cubo donde cada lado mide$x−5$ unidades.

Contestar

1. $x^{4}+x^{3}+x+1$

3. $2x^{4}+7x^{3}−12x^{2}+28x−5$

5. $a^{2}+4ab−2ac+4b^{2}−4bc+c^{2}$

7. $x^{4}−12x^{3}+54x^{2}−108x+81$

9. $x^{3}+6x^{2}+8x$

Ejercicio$\PageIndex{8}$ Special Products

Multiplicar.

$(x+2)^{2}$
$(x−3)^{2}$
$(2x+5)^{2}$
$(3x−7)^{2}$
$(−x+2)^{2}$
$(−9x+1)^{2}$
$(a+6)^{2}$
$(2a−3b)^{2}$
$(\frac{2}{3}x+\frac{3}{4})^{2}$
$(\frac{1}{2}x−\frac{3}{5})^{2}$
$(x^{2}+2)^{2}$
$(x^{2}+y^{2})^{2}$
$(x+4)(x−4)$
$(2x+1)(2x−1)$
$(5x+3)(5x−3)$
$(\frac{1}{5}x−\frac{1}{3})(\frac{1}{5}x+\frac{1}{3})$
$(\frac{3}{2}x+\frac{2}{5})(\frac{3}{2}x−\frac{2}{5})$
$(2x−3y)(2x+3y)$
$(4x−y)(4x+y)$
$(a^{3}−b^{3})(a^{3}+b^{3})$
Se realiza una caja recortando las esquinas y plegando los bordes de una pieza cuadrada de cartón. Se da una plantilla para una caja de cartón con una altura de$2$ pulgadas. Encuentra una fórmula para el volumen, si la pieza inicial de cartón es un cuadrado con lados que miden$x$ pulgadas.
$Captura de pantalla (369) .png$
Figura$\PageIndex{5}$
Se da una plantilla para una caja de cartón con una altura de$x$ pulgadas. Encuentra una fórmula para el volumen, si la pieza inicial de cartón es un cuadrado con lados que miden$12$ pulgadas.
$Captura de pantalla (370) .png$
Figura$\PageIndex{6}$

Contestar

1. $x^{2}+4x+4 $

3. $4x^{2}+20x+25 $

5. $x^{2}−4x+4 $

7. $a^{2}+12a+36 $

9. $\frac{4}{9}x^{2}+x+\frac{9}{16}$

11. $x^{4}+4x^{2}+4$

13. $x^{2}−16 $

15. $25x^{2}−9 $

17. $\frac{9}{4}x^{2}−\frac{4}{25}$

19. $16x^{2}−y^{2}$

21. $V=2x^{2}−16x+32$pulgadas cúbicas

Ejercicio$\PageIndex{9}$ Multiplying Polynomial Functions

Para cada problema, calcule$(f⋅g)(x)$, dadas las funciones.

$f(x)=8x$y$g(x)=3x−5$
$f(x)=x^{2}$y$g(x)=−5x+1$
$f(x)=x−7$y$g(x)=6x−1$
$f(x)=5x+3$y$g(x)=x^{2}+2x−3$
$f(x)=x^{2}+6x−3$y$g(x)=2x^{2}−3x+5$
$f(x)=3x^{2}−x+1$y$g(x)=−x^{2}+2x−1$

Contestar

1. $(f⋅g)(x)=24x^{2}−40x$

3. $(f⋅g)(x)=6x^{2}−43x+7$

5. $(f⋅g)(x)=2x^{4}+9x^{3}−19x^{2}+39x−15$

Ejercicio$\PageIndex{10}$ Multiplying Polynomial Functions

Dado$f(x)=2x−3$ y$g(x)=3x−1$, encuentre lo siguiente

$(f⋅g)(x)$
$(g⋅f)(x)$
$(f⋅g)(0)$
$(f⋅g)(−1)$
$(f⋅g)(1)$
$(f⋅g)(\frac{1}{2})$

Contestar

1. $(f⋅g)(x)=6x^{2}−11x+3$

3. $(f⋅g)(0)=3$

5. $(f⋅g)(1)=−2$

Ejercicio$\PageIndex{11}$ Multiplying Polynomial Functions

Dado$f(x)=5x−1$ y$g(x)=2x^{2}−4x+5$, encuentra lo siguiente.

$(f⋅g)(x) $
$(g⋅f)(x) $
$(f⋅g)(0) $
$(f⋅g)(−1) $
$(f⋅g)(1) $
$(f⋅g)(\frac{1}{2})$
$(f⋅f)(x) $
$(g⋅g)(x)$

Contestar

1. $(f⋅g)(x)=10x^{3}−22x^{2}+29x−5$

3. $(f⋅g)(0)=−5$

5. $(f⋅g)(1)=12$

7. $(f⋅f)(x)=25x^{2}−10x+1$

Ejercicio$\PageIndex{12}$ Discussion Board Topics

Explique por qué$(x+y)^{2}\neq x^{2}+y{2}$.
Explicar cómo multiplicar rápidamente un binomio con su conjugado. Dé un ejemplo.
¿Cuáles son las ventajas y desventajas de usar el dispositivo mnemotécnico FOIL?

Responder

1. Las respuestas pueden variar

3. Las respuestas pueden variar

Search

Text Color

Text Size

Margin Size

Font Type

Productos Especiales

Multiplicar funciones polinomiales

Claves para llevar