1.2: Operaciones con Números Reales

Última actualización
Guardar como PDF

Page ID: 109814

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Revisar las propiedades de números reales.
Simplifica las expresiones que implican agrupar símbolos y exponentes.
Simplificar usando el orden correcto de las operaciones.

Trabajar con números reales

En esta sección, continuamos revisando las propiedades de números reales y sus operaciones. El resultado de sumar números reales se llama la suma ⁵³ y el resultado de restar se llama la diferencia ⁵⁴. Dados los números reales a, b y c, tenemos las siguientes propiedades de adición:

Mesa$\PageIndex{1}$
Identidad Aditiva Propiedad: ⁵⁵	a+0=0+a=a
Propiedad inversa aditiva: ⁵⁶	a+ (−a) = (−a) +a=0
Propiedad Asociativa: ⁵⁷	(a+b) +c=a+ (b+c)
Propiedad Conmutativa: ⁵⁸	a+b=b+a

Es importante señalar que la suma es conmutativa y la resta no lo es. Es decir, el orden en que añadimos no importa y dará el mismo resultado. Sin embargo, esto no es cierto en el caso de la resta.

$5+10=10+5$$5−10≠10−5$

$15=15$$−5≠5$

Utilizamos estas propiedades, junto con la propiedad de doble negativo para números reales, para realizar operaciones secuenciales más involucradas. Para simplificar las cosas, conviértase en una regla general reemplazar primero todas las operaciones secuenciales con suma o resta y luego realizar cada operación en orden de izquierda a derecha.

Ejemplo$\PageIndex{1}$:

Simplificar:$−10−(−10)+(−5)$.

Solución

Reemplazar las operaciones secuenciales y luego realizarlas de izquierda a derecha.

$−10−(−10)+(−5)=−10+10−5$$\color{Cerulean}{Replace −(−) with addition (+)}$.

$\color{Cerulean}{Replace +(−) with subtraction (-).}$

$=0−5$

$=−5$

Responder

$−5$

Sumar o restar fracciones requiere un denominador común ⁵⁹. Supongamos que el denominador común c es un entero distinto de cero y tenemos

$\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$y$\frac{a}{c}−\frac{b}{c}=\frac{a−b}{c}$

Ejemplo$\PageIndex{2}$:

Simplificar:$\frac{2}{9}−\frac{1}{15}+\frac{8}{45}$.

Solución

Primero determinar el mínimo común múltiplo (MCM) de$9, 15, and 45$. El mínimo común múltiplo de todos los denominadores se llama el mínimo común denominador ⁶⁰ (LCD). Comenzamos enumerando los múltiplos de cada denominador dado:

$\{9,18,27,36,45,54,63,72,81,90,\dots\}$$\color{Cerulean}{Multiples of 9}$

$\{15,30,45,60,75,90,\dots\}$$\color{Cerulean}{Multiples of 15}$

$\{45,90,135\dots\}$$\color{Cerulean}{Multiples of \: 45}$

Aquí vemos que el LCM$(9, 15, 45) = 45$. Multiplique el numerador y el denominador de cada fracción por valores que resulten en fracciones equivalentes con el denominador común determinado.

$\frac{2}{9}−\frac{1}{15}+\frac{8}{45}=\frac{2}{9}⋅\color{Cerulean}{\frac{5}{5}}$$−\frac{1}{15}⋅\color{Cerulean}{\frac{3}{3}}$$+\frac{8}{45}$

$=\frac{10}{45}−\frac{3}{45}+\frac{8}{45}$

Una vez que tenemos fracciones equivalentes, con un denominador común, podemos realizar las operaciones en los numeradores y escribir el resultado sobre el denominador común.

$=\frac{10−3+8}{45}$

$=\frac{15}{45}$

Y luego reducir si es necesario,

$=\frac{15\color{Cerulean}{÷15}}{45\color{Cerulean}{÷15}}$

$=\frac{1}{3}$

Responder

$\frac{1}{3}$

Encontrar el LCM usando listas de múltiplos, como se describe en el ejemplo anterior, suele ser muy engorroso. Por ejemplo, intente hacer una lista de múltiplos para$12$ y$81$. Podemos agilizar el proceso de búsqueda del LCM mediante el uso de factores primos.

$12=2^{2}⋅3$

$81=3^{4}$

El múltiplo menos común es el producto de cada factor primo elevado a la potencia más alta. En este caso,

$LCM(12,81)=2^{2}⋅3^{4}=324$

A menudo encontraremos la necesidad de traducir oraciones en inglés que impliquen suma y resta a declaraciones matemáticas. A continuación se presentan algunas traducciones comunes.

$n+2 \color{Cerulean}{The\: sum\: of\: a\: number\: and\: 2.}$

$2−n \color{Cerulean}{The\: difference\: of\: 2\: and\: a\: number.}$

$n−2 \color{Cerulean}{Here\: 2\: is\: subtracted\: from\: a\: number.}$

Ejemplo$\PageIndex{3}$:

¿Qué se$8$ resta de la suma de$3$ y$\frac{1}{2}$?

Solución

Sabemos que la resta no es conmutativa; por lo tanto, debemos cuidar de restar en el orden correcto. Primero, suma$3$$\frac{1}{2}$ y luego resta de la$8$ siguiente manera:

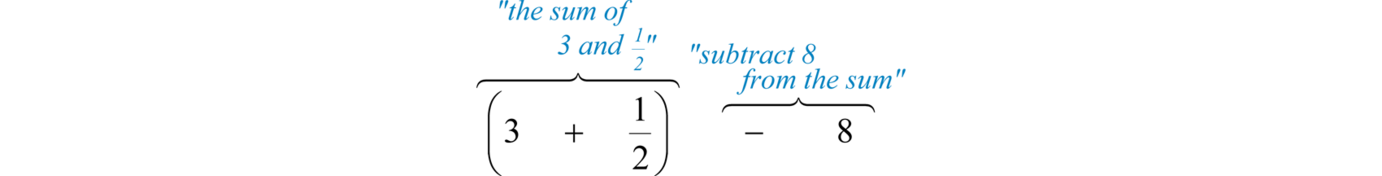
Realizar las operaciones indicadas.

$(3+\frac{1}{2})−8=(\frac{3}{1}⋅\color{Cerulean}{\frac{2}{2}}$$+\frac{1}{2})−8$

$=(\frac{6+1}{2})−8$

$=\frac{7}{2}−\frac{8}{1}⋅\color{Cerulean}{\frac{2}{2}}$

$=\frac{7−16}{2}$

$=−\frac{9}{2}$

Responder

$−\frac{9}{2}$

El resultado de multiplicar números reales se llama producto ⁶¹ y el resultado de dividir se llama cociente ⁶². Dados los números reales a, b y c, tenemos las siguientes propiedades de multiplicación:

Mesa$\PageIndex{2}$
Propiedad Factor Cero: ⁶³	a0=0a=0
Propiedad Identidad Multiplicativa: ⁶⁴	a1=1a=a
Propiedad Asociativa: ⁶⁵	(ab) c=a⋅ (bc)
Propiedad Conmutativa: ⁶⁶	ab=ba

Es importante señalar que la multiplicación es conmutativa y la división no lo es. Es decir, el orden en que nos multiplicamos no importa y dará el mismo resultado. Sin embargo, esto no es cierto de la división.

$5⋅10=10⋅5$$5÷10≠10÷5$

$50=50$$0.5≠2$

Utilizaremos estas propiedades para realizar operaciones secuenciales que impliquen multiplicación y división. Recordemos que el producto de un número positivo y un número negativo es negativo. Además, el producto de dos números negativos es positivo.

Ejemplo$\PageIndex{4}$:

Multiplicar: 5 (−3) (−2) (−4).

Solución

Multiplique dos números a la vez de la siguiente manera:

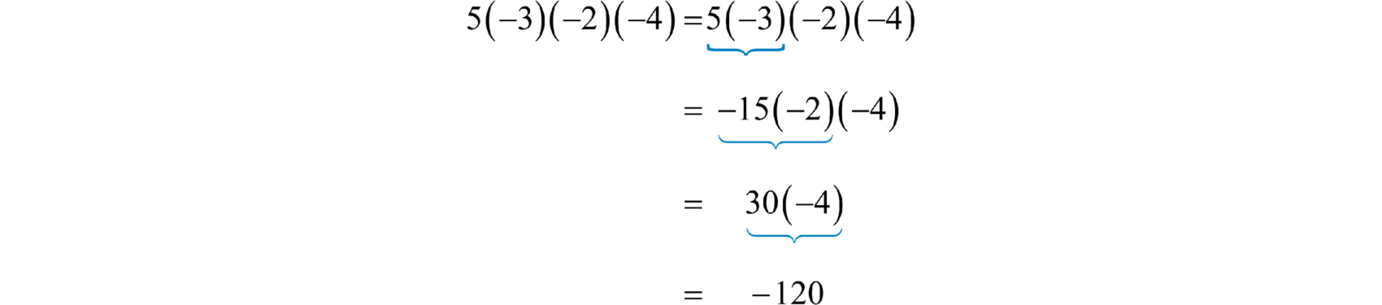
Responder

$−120$

Debido a que la multiplicación es conmutativa, el orden en que nos multiplicamos no afecta la respuesta final. Sin embargo, cuando las operaciones secuenciales implican multiplicación y división, el orden sí importa; de ahí que debemos trabajar las operaciones de izquierda a derecha para obtener un resultado correcto.

Ejemplo$\PageIndex{5}$:

Simplificar: 10÷ (−2) (−5).

Solución

Realizar primero la división; de lo contrario el resultado será incorrecto.

Observe que el orden en que multiplicamos y dividimos sí afecta el resultado. Por lo tanto, es importante realizar las operaciones de multiplicación y división tal como aparecen de izquierda a derecha.

Responder

$25$

El producto de dos fracciones es la fracción formada por el producto de los numeradores y el producto de los denominadores. Es decir, para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores:

$\frac{a}{b}⋅\frac{c}{d}=\frac{ac}{bd}$

Ejemplo$\PageIndex{6}$:

Multiplicar$−\frac{4}{5}⋅\frac{25}{12}$.

Solución

Multiplicar los numeradores y multiplicar los denominadores. Reducir dividiendo cualquier factor común.

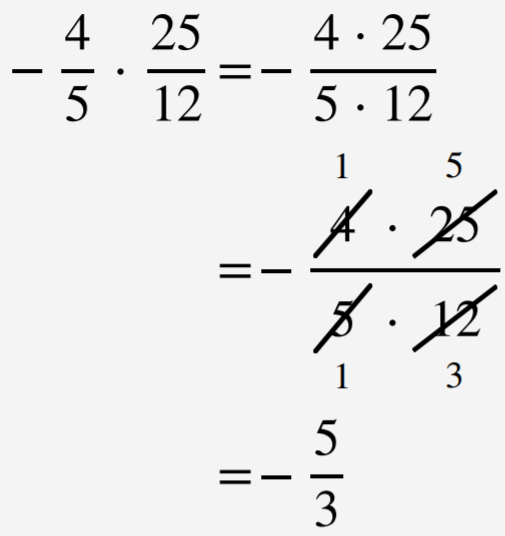Captura de pantalla (133) .png — Figura$\PageIndex{4}$

Respuesta:

$−\frac{5}{3}$

Dos números reales cuyo producto es$1$ se denominan reciprocales ⁶⁷. Por lo tanto,$\frac{a}{b}$ y$\frac{b}{a}$ son recíprocos porque$\frac{a}{b}⋅\frac{b}{a}=\frac{ab}{ab}=1$. Por ejemplo,

$\frac{2}{3}⋅\frac{3}{2}=\frac{6}{6}=1$

Porque su producto es$1, \frac{2}{3}$ y$\frac{3}{2}$ son recíprocos. Algunas otras reciprocas se enumeran a continuación:

$\frac{5}{8}$$\frac{8}{5}$$7$y$\frac{1}{7}$$−\frac{4}{5}$ y$−\frac{5}{4}$

Esta definición es importante porque dividir fracciones requiere que multipliques el dividendo por el recíproco del divisor.

$\frac{a}{b}÷\color{Cerulean}{\frac{c}{d}}$$=\frac { \frac { a } { b } } { \frac { c } { d } } \cdot \color{OliveGreen}{\frac { \frac { d } { c } } { \frac { d } { c } }}$$=\frac { \frac { a } { b } \cdot \frac { d } { c } } { 1 } = \frac { a } { b } \cdot \color{Cerulean}{\frac { d } { c }}$

En general,

$\frac { a } { b } \div \color{Cerulean}{\frac { c } { d }}$$= \frac { a } { b } \cdot \color{Cerulean}{\frac { d } { c }}$$= \frac { a d } { b c }$

Ejemplo$\PageIndex{7}$:

Simplificar:$\frac{5}{4}÷\frac{3}{5}⋅\frac{1}{2}$.

Solución

Realizar la multiplicación y división de izquierda a derecha.

$\frac{5}{4}÷\color{Cerulean}{\frac{3}{5}}$$⋅\frac{1}{2}=\frac{5}{4}⋅\color{Cerulean}{\frac{5}{3}}$$⋅\frac{1}{2}$

$=\frac{5⋅5⋅1}{4⋅3⋅2}$

$=\frac{25}{24}$

En álgebra, a menudo es preferible trabajar con fracciones impropias. En este caso, dejamos la respuesta expresada como una fracción impropia.

Responder

$\frac{25}{24}$

Ejercicio$\PageIndex{1}$

Simplificar:$\frac{1}{2}⋅\frac{3}{4}÷\frac{1}{8}$.

Responder: $3$www.youtube.com/v/4zv-fyepzkk

Agrupación de símbolos y exponentes

En un cómputo donde se involucra más de una operación, los símbolos de agrupación nos ayudan a decirnos qué operaciones realizar primero. Los símbolos de agrupación ⁶⁸ utilizados comúnmente en álgebra son:

$( )$$\color{Cerulean}{Parentheses}$

$[ ]$$\color{Cerulean}{Brackets}$

$\{ \}$$\color{Cerulean}{Braces}$

$-$$\color{Cerulean}{Fraction\: bar}$

Todos los símbolos de agrupación anteriores, así como el valor absoluto, tienen el mismo orden de precedencia. Realice primero operaciones dentro del símbolo de agrupación más interno o valor absoluto.

Ejemplo$\PageIndex{8}$:

Simplificar:$2−(\frac{4}{5}−\frac{2}{15})$.

Solución

Realizar primero las operaciones dentro de los paréntesis.

$2−(\frac{4}{5}−\frac{2}{15})= 2−(\frac{4}{5}⋅\color{Cerulean}{\frac{3}{3}}$$−\frac{2}{15})$

$=2−(\frac{12}{15}−\frac{2}{15})$

$=2−(\frac{10}{15})$

$=\frac{2}{1}⋅\color{Cerulean}{\frac{3}{3}}$$−\frac{2}{3}$

$=\frac{6-2}{3}$

$=\frac{4}{3}$

Respuesta:

$\frac{4}{3}$

Ejemplo$\PageIndex{9}$:

Simplificar:$\frac { 5 - | 4 - ( - 3 ) | } { | - 3 | - ( 5 - 7 ) }$.

Solución

La barra de fracción agrupa el numerador y el denominador. De ahí que se simplifiquen por separado.

$\frac { 5 - | 4 - ( - 3 ) | } { | - 3 | - ( 5 - 7 ) } = \frac { 5 - | 4 + 3 | } { | - 3 | - ( - 2 ) }$

$= \frac { 5 - | 7 | } { | - 3 | + 2 }$

$= \frac { 5 - 7 } { 3 + 2 }$

$= \frac { - 2 } { 5 }$

$= - \frac { 2 } { 5 }$

Respuesta:

$−\frac{2}{5}$

Si un número se repite como factor numerosas veces, entonces podemos escribir el producto en una forma más compacta usando la notación exponencial ⁶⁹. Por ejemplo,

$5⋅5⋅5⋅5=54$

La base ⁷⁰ es el factor y el exponente entero positivo ⁷¹ indica el número de veces que la base se repite como factor. En el ejemplo anterior, la base es$5$ y el exponente es$4$. Los exponentes a veces se indican con el símbolo de intercalación (^) que se encuentra en el teclado,$5^4 = 5*5*5*5$. En general, si a es la base que se repite como factor n veces, entonces

Cuando el exponente es$2$ llamamos al resultado un cuadrado ⁷², y cuando el exponente es$3$ llamamos al resultado un cubo ⁷³. Por ejemplo,

$5^{2}=5⋅5=25$$\color{Cerulean}{"5\: squared”}$

$5^{3}=5⋅5⋅5=125$$\color{Cerulean}{“5\: cubed”}$

Si el exponente es mayor que$3$, entonces$a^{n}$ se lee la notación, “a elevada a la enésima potencia”. La base puede ser cualquier número real,

$(2.5)^{2}=(2.5)(2.5)=6.25$

$(−\frac{2}{3})^{3}=(−\frac{2}{3})(−\frac{2}{3})(−\frac{2}{3})=−\frac{8}{27}$

$(−2)^4=(−2)(−2)(−2)(−2)=16$

$−2^{4}=−1⋅2⋅2⋅2⋅2=−16$

Observe que el resultado de una base negativa con un exponente par es positivo. El resultado de una base negativa con un exponente impar es negativo. Estos hechos suelen confundirse cuando se trata de números negativos. Estudie cuidadosamente los siguientes cuatro ejemplos:

Mesa$\PageIndex{3}$
*La base es$(−3)$.*	*La base es$3$.*
\ ((−3)\).” class="lt-math-6227"> $(−3)^{4}=(−3)(−3)(−3)(−3)=+81$ $(−3)^{3}=(−3)(−3)(−3)=−27$	\ (3\).” class="lt-math-6227"> $−3^{4}=−1⋅3⋅3⋅3⋅3=−81$ $−3^{3}=−1⋅3⋅3⋅3=−27$

Los paréntesis indican que el número negativo se va a utilizar como base.

Ejemplo$\PageIndex{10}$:

Calcular:

$(−\frac{1}{3})^{3}$
$(−\frac{1}{3})^{4}$

Solución

Aquí$−\frac{1}{3}$ está la base para ambos problemas.

1.Usa la base como factor tres veces.

$(−\frac{1}{3})^{3}=(−\frac{1}{3})(−\frac{1}{3})(−\frac{1}{3})$

$=−\frac{1}{27}$

2.Usa la base como factor cuatro veces.

\ ((−\ frac {1} {3}) ^ {4} = (−\ frac {1} {3}) (−\ frac {1} {3}) (−\ frac {1} {3}) (−\ frac {1} {3})

$=+\frac{1}{81}$

RESPUESTAS:

−$\frac{12}{7}$
$\frac{1}{81}$

Ejercicio$\PageIndex{2}$

Simplificar:

$−2^{4}$
$(−2)^{4}$

Responder

1. −16

2. 16

www.youtube.com/v/o3x52psrjtg

Orden de Operaciones

Cuando se van a aplicar varias operaciones dentro de un cálculo, debemos seguir un orden específico para asegurar un solo resultado correcto.

Realice primero todos los cálculos dentro del paréntesis más interno o símbolo de agrupación.
Evaluar todos los exponentes.
Aplicar multiplicación y división de izquierda a derecha.
Realizar todas las operaciones restantes de suma y resta duran de izquierda a derecha.

Obsérvese que la multiplicación y división deben trabajarse de izquierda a derecha. Debido a esto, a menudo es razonable realizar la división antes de la multiplicación.

Ejemplo$\PageIndex{11}$:

Simplificar:$5^{3} − 24 ÷ 6 ⋅ \frac{1}{2} + 2.$

Solución

Primero, evalúe$5^{3}$ y luego realice la multiplicación y división tal como aparecen de izquierda a derecha.

\ begin {alineado} 5 ^ {3} - 24\ div 6\ cdot\ frac {1} {2} + 2 & = 5 ^ {3} - 24\ div 6\ cdot\ frac {1} {2} + 2\\ & = 125 - 24\ div 6\ cdot\ frac {1} {2} + 2\\ & = 125 - 4\ cdot\ frac {} {2} + 2\\ & = 125 - 2 + 2\\ & = 123 + 2\\ & = 125\ final {alineado}

Multiplicar primero habría llevado a un resultado incorrecto.

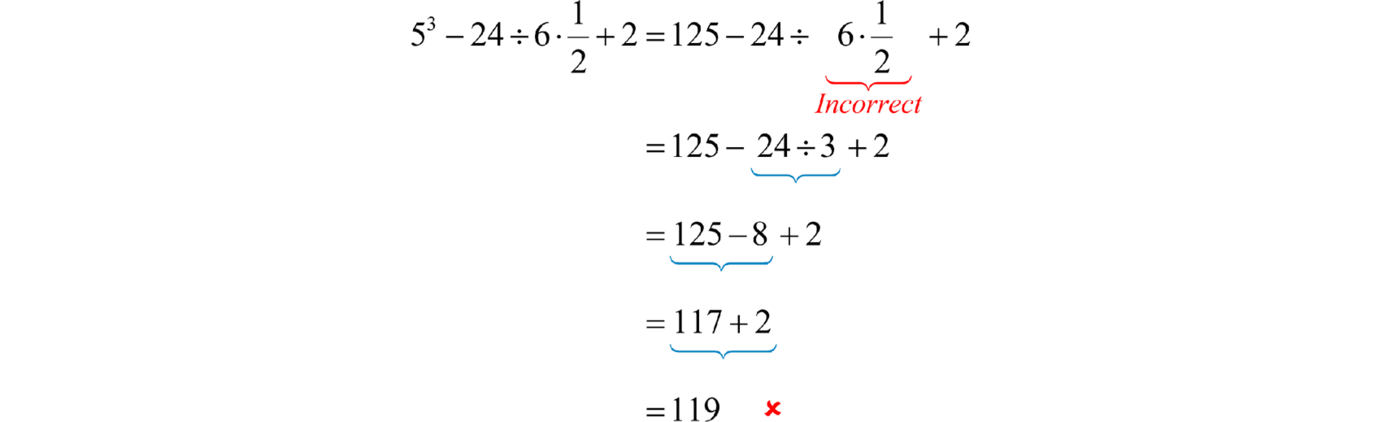
Respuesta:

$125$

Ejemplo$\PageIndex{12}$:

Simplificar:$- 10 - 5 ^ { 2 } + ( - 3 ) ^ { 4 }$.

Solución

Tenga cuidado de identificar correctamente la base al cuadrar.

$\begin{aligned} - 10 - 5 ^ { 2 } + ( - 3 ) ^ { 4 } & = - 10 - 25 + 81 \\ & = - 35 + 81 \\ & = 46 \end{aligned}$

Respuesta:

$46$

Es menos probable que cometamos un error si trabajamos una operación a la vez. Algunos problemas pueden implicar un valor absoluto, en cuyo caso le asignamos el mismo orden de precedencia que los paréntesis.

Ejemplo$\PageIndex{13}$:

Simplificar:$7 - 5 \left| - 2 ^ { 2 } + ( - 3 ) ^ { 2 }\right.$.

Solución

Comience por realizar primero las operaciones dentro del valor absoluto.

$\begin{aligned} 7 - 5 \left| - 2 ^ { 2 } + ( - 3 ) ^ { 2 } \right| & = 7 - 5 | - 4 + 9 | \\ & = 7 - 5 | 5 | \\ & = 7 - 5 \cdot 5 \\ & = 7 - 25 \\ & = - 18 \end{aligned}$

Restar$7−5$ primero conducirá a resultados incorrectos.

Respuesta:

$−18$

Ejercicio$\PageIndex{3}$

Simplificar:$- 6 ^ { 2 } - \left[ - 15 - ( - 2 ) ^ { 3 } \right] - ( - 2 ) ^ { 4 }$.

Responder

$-45$

www.youtube.com/v/dnaviqzlpa0

Claves para llevar

La suma es conmutativa y la resta no lo es. Además, la multiplicación es conmutativa y la división no lo es.
Sumar o restar fracciones requiere un denominador común; multiplicar o dividir fracciones no lo hace.
Los símbolos de agrupación indican qué operaciones realizar primero. Generalmente agrupamos las operaciones matemáticas con paréntesis, corchetes, llaves y la barra de fracción. También agrupamos las operaciones dentro de valores absolutos. Todas las agrupaciones tienen el mismo orden de precedencia: las operaciones dentro de la agrupación más interna se realizan primero.
Cuando se usa notación exponencial$a^{n}$, la base a se usa como factor n veces. Los paréntesis indican que se va a utilizar como base un número negativo. Por ejemplo,$(−5)^{2}$ es positivo y$−5^{2}$ es negativo.
Para asegurar un único resultado correcto al aplicar operaciones dentro de un cálculo, siga el orden de las operaciones. Primero, realizar operaciones en los paréntesis o agrupamientos más internos. A continuación, simplifique todos los exponentes. Realizar operaciones de multiplicación y división de izquierda a derecha. Finalmente, realizar operaciones de suma y resta de izquierda a derecha.

Ejercicio$\PageIndex{4}$

Realizar las operaciones. Reducir todas las fracciones a los términos más bajos.

$33−(−15)+(−8)$
$−10−9+(−6)$
$−23+(−7)−(−10)$
$−1−(−1)−1$
$\frac{1}{2}+\frac{1}{3}−\frac{1}{6}$
$−\frac{1}{5}+\frac{1}{2}−\frac{1}{10}$
$\frac{2}{3}−(−\frac{1}{4})−\frac{1}{6}$
$−\frac{3}{2}−(−\frac{2}{9})−\frac{5}{6}$
$\frac{3}{4}−(−\frac{1}{2})−\frac{5}{8}$
$−\frac{1}{5}−\frac{3}{2}−(−\frac{7}{10})$
Restar$3$ de$10$.
Restar$−2$ de$16$.
Restar$−\frac{5}{6}$ de$4$.
Restar$−\frac{1}{2}$ de$\frac{3}{2}$.
Calcular la suma de$−10$ y$25$.
Calcular la suma de$−30$ y$−20$.
Encuentra la diferencia de$10$ y$5$.
Encuentra la diferencia de$−17$ y$−3$.

Responder

1. $40$

3. $−20$

5. $\frac{2}{3}$

7. $\frac{3}{4}$

9. $\frac{5}{8}$

11. $7$

13. $\frac{29}{6}$

15. $15$

17. $5$

Ejercicio$\PageIndex{5}$

La fórmula$d = | b − a |$ da la distancia entre dos puntos cualesquiera en una recta numérica. Determine la distancia entre los números dados en una recta numérica.

$10$y$15$
$6$y$22$
$0$y$12$
$−8$y$0$
$−5$y$−25$
$−12$y$−3$

Responder

1. 5 unidades

3. 12 unidades

5. 20 unidades

Ejercicio$\PageIndex{6}$

Determinar el recíproco de lo siguiente.

$\frac{1}{3}$
$\frac{2}{5}$
$−\frac{3}{4}$
$−12$
$a$donde$a ≠ 0$
$\frac{1}{a}$
$\frac{a}{b}$donde$a ≠ 0$
$\frac{1}{ab}$

Responder

1. $3$

3. $−\frac{4}{3}$

5. $\frac{1}{a}$

7. $\frac{b}{a}$

Ejercicio$\PageIndex{7}$

Realizar las operaciones.

$−4 (−5) ÷ 2$
$(−15) (−3) ÷ (−9)$
$−22 ÷ (−11) (−2)$
$50 ÷ (−25) (−4)$
$\frac{2}{3} (−\frac{9}{10})$
$−\frac{5}{8} (−\frac{16}{25})$
$\frac{7}{6} (−\frac{6}{7})$
$−\frac{15}{9} (\frac{9}{5})$
$\frac{4}{5} (−\frac{2}{5}) ÷ \frac{16}{25}$
$(−\frac{9}{2}) (−\frac{3}{2}) ÷ \frac{27}{16}$
$\frac{8}{5} ÷ \frac{5}{2} ⋅ \frac{15}{40}$
$\frac{3}{16} ÷ \frac{5}{8} ⋅ \frac{1}{2}$
Encuentra el producto de$12$ y$7$.
Encuentra el producto de$−\frac{2}{3}$ y$12$.
Encuentra el cociente de$−36$ y$12$.
Encuentra el cociente de$−\frac{3}{4}$ y$9$.
Restar$10$ de la suma de$8$ y$−5$.
Restar$−2$ de la suma de$−5$ y$−3$.
Joe gana$$18.00$ por hora y “tiempo y medio” por cada hora que trabaja a lo largo de$40$ horas. ¿Cuál es su paga por$45$ horas de trabajo esta semana?
Billy compró$12$ botellas de agua$$0.75$ por botella,$5$ libras de dulces surtidos$$4.50$ por libra y$15$ paquetes de palomitas de maíz para microondas que cuestan$$0.50$ cada uno para su fiesta. ¿Cuál era su factura total?
James y Mary viajaron a casa desde la universidad para las vacaciones de Acción de Gracias. Compartieron la conducción, pero Mary condujo el doble de distancia que James. Si Mary condujo por$210$ millas, entonces ¿cuántas millas fue todo el viaje?
Un tablón de$6 \frac{3}{4}$ pie se va a cortar en$3$ trozos de igual longitud. ¿Cuál será la longitud de cada pieza?
Una estudiante obtuvo$72, 78, 84,$ y$90$ puntos en sus primeros cuatro exámenes de álgebra. ¿Cuál fue su puntaje promedio en las pruebas? (Recordemos que el promedio se calcula sumando todos los valores en un conjunto y dividiendo ese resultado por el número de elementos en el conjunto.)
La temperatura más fría de la Tierra,$−129$ °F, se registró en$1983$ en la estación Vostok, Antártida. La temperatura más calurosa de la Tierra,$136$ °F, se registró$1922$ en Al' Aziziyah, Libia. Calcular el rango de temperatura en la Tierra.

Responder

1. $10$

3. $−4$

5. $−\frac{3}{5}$

7. $−1$

9. $−\frac{1}{2}$

11. $\frac{6}{25}$

13. $84$

15. $−3$

17. $−7$

19. $$855$

21. $315$millas

23. $81$puntos

Ejercicio$\PageIndex{8}$

Realizar las operaciones.

$7 − \{3 − [−6 − (10)]\}$
$− (9 − 12) − [6 − (−8 − 3)]$
$\frac{1}{2} \{5 − (10 − 3)\}$
$\frac{2}{3} \{−6 + (6 − 9)\}$
$5 \{2 [3 (4 − \frac{3}{2} )]\}$
$\frac{1}{2} \{−6 [− (\frac{1}{2} − \frac{5}{3})]\}$
$\frac { 5 - | 5 - ( - 6 ) | } { | - 5 | - | - 3 | }$
$\frac { | 9 - 12 | - ( - 3 ) } { | - 16 | - 3 ( 4 ) }$
$\frac { - | - 5 - ( - 7 ) | - ( - 2 ) } { | - 2 | + | - 3 | }$
$\frac { 1 - | 9 - ( 3 - 4 ) | } { - | - 2 | + ( - 8 - ( - 10 ) ) }$

Responder

1. $−1$2

3. $−1$

5. $75$

7. $−3$

9. $0$

Ejercicio$\PageIndex{9}$

Realizar las operaciones.

$12^{2}$
$(−12)^{2}$
$−12^{2}$
$−(−12)^{2}$
$−5^{4}$
$(−5)^{4}$
$(−\frac{1}{2})^{3}$
$−(−\frac{1}{2})^{3}$
$−(−\frac{3}{4})^{2}$
$−(−\frac{5}{2})^{3}$
$(−1)^{22}$
$(−1)^{13}$
$−(−1)^{12}$
$−(−1)^{5}$
$−10^{2}$
$−10^{4}$

Responder

1. $144$

3. $−144$

5. $−625$

7. $−\frac{1}{8}$

9. $−\frac{9}{16}$

11. $1$

13. $−1$

15. $−100$

Ejercicio$\PageIndex{10}$

Simplificar.

$5 − 3 (4 − 3^{2})$
$8 − 5 (3 − 3^{2})$
$(−5)^{2} + 3 (2 − 4^{2})$
$6 − 2 (−5^{2} + 4 ⋅ 7)$
$5 − 3 [3 (2 − 3^{2}) + (−3)^{2}]$
$10 − 5 [(2 − 5)^{2} − 3]$
$[5^{2} − 3^{2} ] − [2 − (5 + (−4)^{2} )]$
$−7^{2} − [ (2 − 7)^{2} − (−8)^{2} ]$
$\frac{3}{16} ÷ (\frac{5}{12} −\frac{1}{2} +\frac{2}{3}) ⋅ 4$
$6 \cdot \left[ \left( \frac { 2 } { 3 } \right) ^ { 2 } - \left( \frac { 1 } { 2 } \right) ^ { 2 } \right] \div ( - 2 ) ^ { 2 }$
$\frac { 3 - 2 \cdot 5 + 4 } { 2 ^ { 2 } - 3 ^ { 2 } }$
$\frac { \left( 3 + ( - 2 ) ^ { 2 } \right) \cdot 4 - 3 } { - 4 ^ { 2 } + 1 }$
$\frac { - 5 ^ { 2 } + ( - 3 ) ^ { 2 } \cdot 2 - 3 } { 8 ^ { 2 } + 6 ( - 10 ) }$
$\frac { ( - 4 ) ^ { 2 } + ( - 3 ) ^ { 3 } } { - 9 ^ { 2 } - \left( - 12 + 2 ^ { 2 } \right) * 10 }$
$−5^{2} − 2 |−5| $
$−2^{4} + 6 | 2^{4} − 5^{2} |$
$− (4− | 7^{2} − 8^{2} |)$
$−3 (5 − 2 |−6|)$
$(−3)^{2}− | −2 + (−3)^{3} | − 4^{2}$
$−5^{2} − 2 | 3^{3} − 2^{4} | − (−2)^{5}$
$5 ⋅ |−5| − (2 − |−7|)^{3}$
$10^{2} + 2 ( |−5|^{3} − 6^{3})$
$\frac{2}{3} − | \frac{1}{2} − (−\frac{4}{3})^{2} |$
$−24 | \frac{10}{3} − \frac{1}{2} ÷ \frac{1}{5} |$
Calcular la suma de los cuadrados de los tres primeros enteros impares positivos consecutivos.
Calcular la suma de los cuadrados de los tres primeros enteros pares positivos consecutivos.
¿Qué se$6$ resta de la suma de los cuadrados de$5$ y$8$?
¿Qué se$5$ resta de la suma de los cubos de$2$ y$3$?

Responder

1. $20$

3. $−17$

5. $41$

7. $35$

9. $\frac{9}{7}$

11. $\frac{3}{5}$

13. $−\frac{5}{2}$

15. $−35$

17. $11$

19. $−36$

21. $150$

23. $−\frac{11}{18}$

25. $35$

27. $83$

Ejercicio$\PageIndex{11}$

¿Qué es PEMDAS y qué le falta?
¿$0$Tiene un recíproco? Explique.
Explique por qué necesitamos un denominador común para sumar o restar fracciones.
$(−10)^{4}$Explique por qué es positivo y$−10^{4}$ es negativo.

Responder

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

⁵³ El resultado de sumar.

⁵⁴ El resultado de restar.

⁵⁵ Dado cualquier número real$a, a + 0 = 0 + a = a$.

⁵⁶ Dado cualquier número real$a, a + (−a) = (−a) + a = 0$.

⁵⁷ Dados números reales$a, b$ y$c, (a + b) + c = a + (b + c)$.

⁵⁸ Dados números reales$a$ y$b$,$a + b = b + a$.

⁵⁹ Un denominador que es compartido por más de una fracción.

⁶⁰ El mínimo común múltiplo de un conjunto de denominadores.

⁶¹ El resultado de multiplicar.

⁶² El resultado de dividir.

⁶³ Dado cualquier número real$a, a ⋅ 0 = 0 ⋅ a = 0 .$

⁶⁴ Dado cualquier número real$a, a ⋅ 1 = 1 ⋅ a = a .$

⁶⁵ Dados los números reales$a, b$ y$c, (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c) . $

⁶⁶ Dados los números reales$a$ y$b, a ⋅ b = b ⋅ a.$

⁶⁷ Dos números reales cuyo producto es$1$.

⁶⁸ Los paréntesis, corchetes, llaves y la barra de fracciones son los símbolos comunes utilizados para agrupar expresiones y operaciones matemáticas dentro de un cálculo.

⁶⁹ La notación compacta$a^{n}$ utilizada cuando un factor$a$ se repite$n$ veces.

⁷⁰ El factor$a$ en la notación exponencial$a^{n}$.

⁷¹ El entero positivo$n$ en la notación exponencial$a^{n}$ que indica el número de veces que se usa la base como factor.

⁷² El resultado cuando el exponente de cualquier número real es$2$.

⁷³ El resultado cuando el exponente de cualquier número real es$3$.

Search

Text Color

Text Size

Margin Size

Font Type