4.5: Funciones racionales - Multiplicación y División

Última actualización
Guardar como PDF

Page ID: 109795

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Identificar restricciones al dominio de una función racional.
Simplifica las funciones racionales.
Multiplicar y dividir las funciones racionales.

Identificación de restricciones y simplificación de funciones racionales

Las funciones racionales ²⁵ tienen la forma

$r ( x ) = \dfrac { p ( x ) } { q ( x ) }$,

donde$p(x)$ y$q(x)$ son polinomios y$q(x)≠0$. El dominio de una función racional ²⁶ consiste en todos los números reales$x$ excepto aquellos en los que el denominador$q(x)=0$. Las restricciones ²⁷ son los números reales para los que no se define la expresión. A menudo expresamos el dominio de una función racional en términos de sus restricciones. Por ejemplo, considere la función

$f ( x ) = \dfrac { x ^ { 2 } - 4 x + 3 } { x ^ { 2 } - 5 x + 6 }$

que se puede escribir en forma factorizada

$f ( x ) = \dfrac { ( x - 1 ) ( x - 3 ) } { ( x - 2 ) ( x - 3 ) }$

Debido a que las expresiones racionales son indefinidas cuando el denominador es$0$, deseamos encontrar los valores para$x$ que lo hagan$0$. Para ello, aplique la propiedad zero product. Establezca cada factor en el denominador igual a$0$ y resuelva.

$\begin{array} { c } { ( x - 2 )\: ( x - 3 ) = 0 } \\ { x - 2 = 0 \quad \text { or } \quad x - 3 = 0 } \\ { x = 3 }\quad\quad\quad\quad {x=3} \end{array}$

Por lo tanto, la función original se define para cualquier número real excepto$2$ y$3$. Podemos expresar su dominio usando la notación de la siguiente manera:

$\begin{array} { l l } { \color{Cerulean} { Set-builder\: notation } } & { \color{Cerulean} { Interval \:notation } } \\ \{ x | x \neq 2,3 \} & {( - \infty , 2 ) \cup ( 2,3 ) \cup ( 3 , \infty ) } \end{array}$

Las restricciones al dominio de una función racional están determinadas por el denominador. Una vez determinadas las restricciones podemos cancelar factores y obtener una función equivalente de la siguiente manera:

Es importante señalar que no$1$ es una restricción al dominio porque la expresión se define como$0$ cuando el numerador es$0$. De hecho,$x=1$ es una raíz. Esta función se representa a continuación:

Observe que hay una asíntota vertical en la restricción$x=2$ y la gráfica se deja indefinida en la restricción$x=3$ como lo indica el punto abierto, o agujero, en la gráfica. Graficar las funciones racionales en general está más allá del alcance de este libro de texto. Sin embargo, es útil en este punto saber que las restricciones son una parte importante de la gráfica de funciones racionales.

Ejemplo$\PageIndex{1}$:

Declarar las restricciones y simplificar:$g ( x ) = \dfrac { 24 x ^ { 7 } } { 6 x ^ { 5 } }$

Solución

En este ejemplo, la función está indefinida donde$x$ está$0$.

$g ( 0 ) = \dfrac { 24 ( 0 ) ^ { 7 } } { 6 ( 0 ) ^ { 5 } } = \dfrac { 0 } { 0 } \quad \color{Cerulean}{undefined}$

Por lo tanto, el dominio consiste en todos los números reales$x$, donde$x≠0$. Con esta comprensión, podemos simplificar reduciendo la expresión racional a los términos más bajos. Cancelar factores comunes.

$g ( x ) = \dfrac { \stackrel{4\:\:\:\: x ^ { 2 }}{\cancel{24}\:\:\: \cancel{x^{7}}} } { \cancel{6}\:\:\:\:\: \cancel{x ^ { 8 }} } = 4 x ^ { 2 }$

Contestar

$g ( x ) = 4 x ^ { 2 }$, donde$x≠0$

Ejemplo$\PageIndex{2}$:

Indicar las restricciones y simplificar:$f ( x ) = \dfrac { 2 x ^ { 2 } + 5 x - 3 } { 4 x ^ { 2 } - 1 }$.

Solución

Primero, factorizar el numerador y el denominador.

$f ( x ) = \dfrac { 2 x ^ { 2 } + 5 x - 3 } { 4 x ^ { 2 } - 1 } = \dfrac { ( 2 x - 1 ) ( x + 3 ) } { ( 2 x + 1 ) ( 2 x - 1 ) }$

Cualquier$x$ -valor que haga que el denominador sea cero es una restricción. Para encontrar las restricciones, primero establezca el denominador igual a cero y luego resuelva

$( 2 x + 1 ) ( 2 x - 1 ) = 0$

$\begin{array} { r l } { 2 x + 1 = 0 } & { \text { or } \quad 2 x - 1 = 0 } \\ { 2 x = - 1 } & \quad\quad\quad\quad{ 2 x = 1 } \\ { x = - \dfrac { 1 } { 2 } } &\quad\quad\quad\quad\: { x = \dfrac { 1 } { 2 } } \end{array}$

Por lo tanto,$x≠±\dfrac{1}{2}$. Con este entendimiento, podemos cancelar cualquier factor común.

$\begin{aligned} f ( x ) & = \dfrac {\cancel{ ( 2 x - 1 )} ( x + 3 ) } { ( 2 x + 1 ) \cancel{( 2 x -1)} } \\ & = \dfrac { x + 3 } { 2 x + 1 } \end{aligned}$

Respuesta:

$f ( x ) = \dfrac { x + 3 } { 2 x + 1 }$, donde$x \neq \pm \dfrac { 1 } { 2 }$

Definimos lo contrario de un polinomio$P$ para ser$−P$. Encontrar lo contrario de un polinomio requiere la aplicación de la propiedad distributiva. Por ejemplo, lo contrario del polinomio$(x−3)$ se escribe como

$\begin{aligned} - ( x - 3 ) & = - 1 \cdot ( x - 3 ) \\ & = - x + 3 \\ & = 3 - x \end{aligned}$

Esto nos lleva a la propiedad binomial opuesta ²⁸,$−(a−b)=(b−a)$. Se debe tener cuidado de no confundir esto con el hecho de que$(a+b)=(b+a)$. Este es el caso porque la adición es conmutativa. En general,

$\begin{array} { c |} -(a-b)=(b-a)\\\text{or}\\\dfrac{b-a}{a-b}=-1 \end{array} \begin{array}{c} (a-b)=(a+b)\\\text{or}\\ \dfrac{b+a}{a+b}=1\end{array}$

Además, es importante recordar que

$\dfrac { - a } { b } = - \dfrac { a } { b } = \dfrac { a } { - b }$

En otras palabras, se muestra una fracción negativa colocando el signo negativo ya sea en el numerador, frente a la barra de fracciones, o en el denominador. Generalmente, se evitan los denominadores negativos.

Ejemplo$\PageIndex{3}$:

Indicar las restricciones y simplificar:$\dfrac { 25 - x ^ { 2 } } { x ^ { 2 } - 10 x + 25 }$.

Solución

Comience por factorizar el numerador y el denominador.

$\begin{aligned} \dfrac { 25 - x ^ { 2 } } { x ^ { 2 } - 10 x + 25 } & = \dfrac { ( 5 - x ) ( 5 + x ) } { ( x - 5 ) ( x - 5 ) } \\ & = \dfrac { \color{Cerulean}{- 1 \cdot ( x - 5 ) }\color{black}{(} 5 + x ) } { ( x - 5 ) ( x - 5 ) }\quad\quad\quad\quad\color{Cerulean}{Opposite\:binomial\:property.} \\ & = \dfrac { - 1 \cdot \cancel{( x - 5 )} ( 5 + x ) } { \cancel{( x - 5 )} ( x - 5 ) } \quad\color{Cerulean}{Cancel.} \\ & = - \dfrac { x + 5 } { x - 5 } \end{aligned}$

Respuesta:

$ - \dfrac { x + 5 } { x - 5 }$, donde$x≠5$

Es importante recordar que solo podemos cancelar factores de un producto. Un error común es cancelar términos. Por ejemplo,

$\dfrac {\cancel{ x ^ { 2} } + 7 x - 30 } { \cancel{x ^ { 2} } - 7 x + 12 } \\ \color{red}{incorrect!}$$\begin{array} { c } { \dfrac { \cancel{x} + 10 } { \cancel{x} - 4 } } \\ { \color{red} { incorrect! } } \end{array}$$\dfrac { 2 \cancel{x-1}} {\cancel{x-1} } \\ \color{red}{incorrect!}$

Ejercicio$\PageIndex{1}$

Indicar las restricciones y simplificar:$\dfrac { x - 2 x ^ { 2 } } { 4 x ^ { 4 } - x ^ { 2 } }$.

Contestar

$- \dfrac { 1 } { x ( 2 x + 1 ) }$, donde$x \neq 0 , \pm \dfrac { 1 } { 2 }$

www.youtube.com/V/ek2qw7ogxby

En algunos ejemplos, haremos una suposición amplia de que el denominador es distinto de cero. Cuando hacemos esa suposición, no necesitamos determinar las restricciones.

Ejemplo$\PageIndex{4}$:

Simplificar:$\dfrac { x ^ { 3 } - 2 x ^ { 2 } y + 4 x y ^ { 2 } - 8 y ^ { 3 } } { x ^ { 4 } - 16 y ^ { 4 } }$. (Supongamos que todos los denominadores son diferentes de cero.)

Solución

Factorizar el numerador por agrupación. Factorizar el denominador usando la fórmula para una diferencia de cuadrados.

$\begin{aligned} \dfrac { x ^ { 3 } + 4 x y ^ { 2 } - 2 x ^ { 2 } y - 8 y ^ { 3 } } { x ^ { 4 } - 16 y ^ { 4 } } & = \dfrac { x \left( x ^ { 2 } + 4 y ^ { 2 } \right) - 2 y \left( x ^ { 2 } + 4 y ^ { 2 } \right) } { \left( x ^ { 2 } + 4 y ^ { 2 } \right) \left( x ^ { 2 } - 4 y ^ { 2 } \right) } \\ & = \dfrac { \left( x ^ { 2 } + 4 y ^ { 2 } \right) ( x - 2 y ) } { \left( x ^ { 2 } + 4 y ^ { 2 } \right) ( x + 2 y ) ( x - 2 y ) } \end{aligned}$

A continuación, cancelar factores comunes.

$= \dfrac { \stackrel{1}{\cancel{\left( x ^ { 2 } + 4 y ^ { 2 } \right)}}\stackrel{1}{ \cancel{\left( x - 2y \right)}} } { { \cancel{\left( x ^ { 2 } + 4 y ^ { 2 } \right) }} ( x + 2 y )\cancel{ ( x - 2 y )} } \\ = \dfrac{1}{x+2y}$

Nota

Cuando todo el numerador o denominador cancela un factor de$1$ siempre permanece.

Respuesta:

$ \dfrac { 1 } { x + 2 y }$

Ejemplo$\PageIndex{5}$:

Dado$f ( x ) = x ^ { 2 } - 2 x + 5$, simplificar$\dfrac { f ( x ) - f ( 3 ) } { x - 3 }$.

Solución

Empezar por calcular$f(3)$.

$\begin{aligned} f ( 3 ) & = ( 3 ) ^ { 2 } - 2 ( 3 ) + 5 \\ & = 9 - 6 + 5 \\ & = 3 + 5 \\ & = 8 \end{aligned}$

A continuación, sustituya en el cociente que se va a simplificar.

$\begin{aligned} \dfrac { f ( x ) - f ( 3 ) } { x - 3 } & = \dfrac { x ^ { 2 } - 2 x + 5 - 8 } { x - 3 } \\ & = \dfrac { x ^ { 2 } - 2 x - 3 } { x - 3 } \\ & = \dfrac { ( x + 1 ) ( x - 3 ) } { ( x - 3 ) } \\ & = x + 1 \end{aligned}$

Respuesta:

$x+1$, donde$x≠3$

Una cantidad importante en matemáticas de nivel superior es el cociente de diferencia ²⁹:

$\dfrac { f ( x + h ) - f ( x ) } { h }$, donde$h \neq 0$

Esta cantidad representa la pendiente de la línea que conecta dos puntos en la gráfica de una función. La línea que pasa por los dos puntos se denomina línea secante ³⁰.

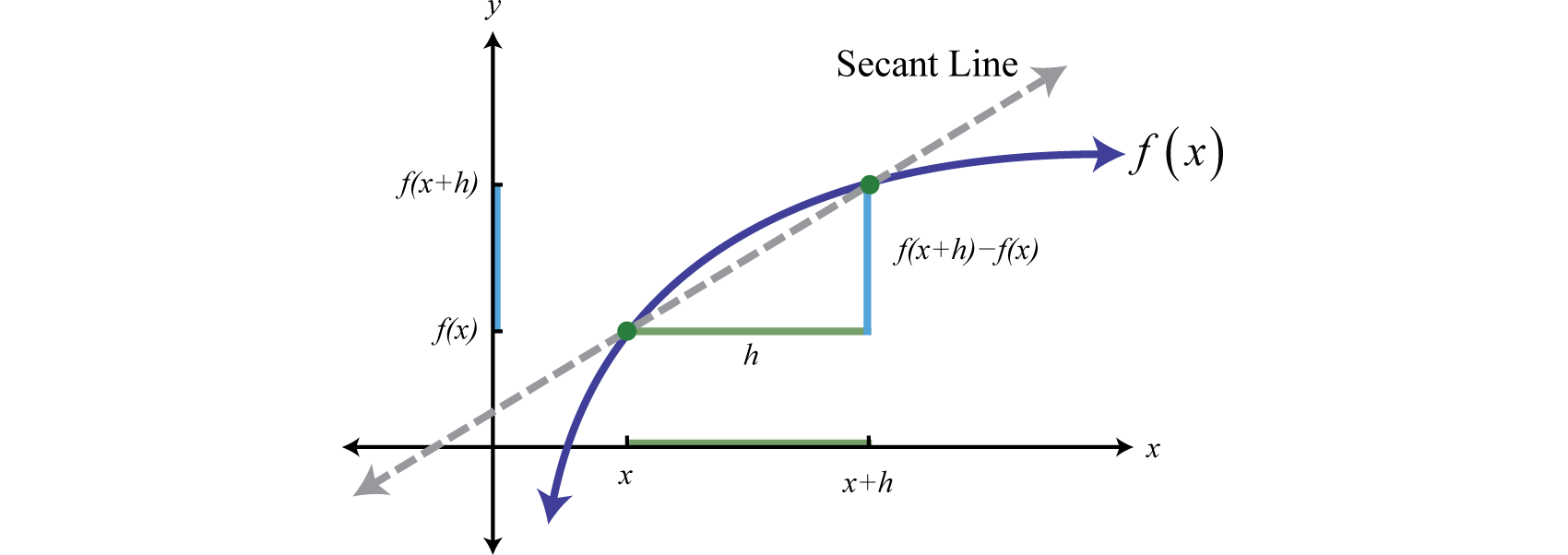
Calcular el cociente de diferencia para muchas funciones diferentes es una habilidad importante para aprender en álgebra intermedia. Nos encontraremos con esta cantidad a menudo a medida que avanzamos en este libro de texto. Al calcular el cociente de diferencia asumimos que el denominador es distinto de cero.

Ejemplo$\PageIndex{6}$:

Dado$g ( x ) = - 2 x ^ { 2 } + 1$, simplificar$\dfrac { g ( x + h ) - g ( x ) } { h }$.

Solución

$\begin{aligned} \dfrac { g ( x + h ) - g ( x ) } { h } & = \dfrac { \left( - 2 ( x + h ) ^ { 2 } + 1 \right) - \left( - 2 x ^ { 2 } + 1 \right) } { h } \\ & = \dfrac { - 2 \left( x ^ { 2 } + 2 x h + h ^ { 2 } \right) + 1 + 2 x ^ { 2 } - 1 } { h } \\ &= { \dfrac { - 2 x ^ { 2 } - 4 x h - 2 h ^ { 2 } + 1 + 2 x ^ { 2 } - 1 } { h } } \\ & = \dfrac { - 4 x h - 2 h ^ { 2 } } { h } \\ & = - 4 x - 2 h \end{aligned}$

Respuesta:

$-4x-2h$

Ejercicio$\PageIndex{2}$

Dado$f ( x ) = x ^ { 2 } - x - 1$, simplificar$\dfrac { f ( x + h ) - f ( x ) } { h }$.

Contestar

$2 x - 1 + h$

www.youtube.com/v/xyofirdnwws

Multiplicar y dividir funciones racionales

Al multiplicar fracciones, podemos multiplicar los numeradores y denominadores juntos y luego reducir. La multiplicación de expresiones racionales se realiza de manera similar. En general, dado polinomios$P, Q, R$, y$S$, donde$Q≠0$ y$S≠0$, tenemos

$\dfrac { P } { Q } \cdot \dfrac { R } { S } = \dfrac { P R } { Q S }$

Las restricciones al dominio de un producto consisten en las restricciones de cada función.

Ejemplo$\PageIndex{7}$:

Dado$f ( x ) = \dfrac { 9 x ^ { 2 } - 25 } { x - 5 }$ y$g ( x ) = \dfrac { x ^ { 2 } - 2 x - 15 } { 3 x + 5 }$, encontrar$( f \cdot g ) ( x )$ y determinar las restricciones al dominio.

Solución

En este caso, el dominio de$f$ consiste en todos los números reales excepto$5$, y el dominio de$g$ consiste en todos los números reales excepto$−\dfrac{5}{3}$. Por lo tanto, el dominio del producto consiste en todos los números reales excepto$5$ y$−\dfrac{5}{3}$. Multiplica las funciones y luego simplifica el resultado.

$\begin{aligned} ( f \cdot g ) ( x ) & = f ( x ) \cdot g ( x ) \\ & = \dfrac { 9 x ^ { 2 } - 25 } { x - 5 } \cdot \dfrac { x ^ { 2 } - 2 x - 15 } { 3 x + 5 } \\ & = \dfrac { ( 3 x + 5 ) ( 3 x - 5 ) } { x - 5 } \cdot \dfrac { ( x - 5 ) ( x + 3 ) } { 3 x + 5 } \quad\quad\color{Cerulean}{Factor.} \\ & = \dfrac {\cancel{ ( 3 x + 5 )} ( 3 x - 5 ) \cancel{( x - 5 )} ( x + 3 ) } { \cancel{( x - 5 )}\cancel{ ( 3 x + 5 )} }\quad\quad\quad\color{Cerulean}{Cancel.} \\ & = ( 3 x - 5 ) ( x + 3 ) \end{aligned}$

Respuesta:

$( f \cdot g ) ( x ) = ( 3 x - 5 ) ( x + 3 )$, donde$x \neq 5 , - \dfrac { 5 } { 3 }$

Para dividir dos fracciones, multiplicamos por el recíproco del divisor. La división de expresiones racionales se realiza de manera similar. En general, dado polinomios$P, Q, R$, y$S$, donde$Q≠0, R≠0$, y$S≠0$, tenemos

$\dfrac { P } { Q } \div \dfrac { R } { S } = \dfrac { P } { Q } \cdot \dfrac { S } { R } = \dfrac { P S } { Q R }$

Las restricciones al dominio de un cociente consistirán en las restricciones de cada función así como las restricciones al recíproco del divisor.

Ejemplo$\PageIndex{8}$:

Dado$f ( x ) = \dfrac { 2 x ^ { 2 } + 13 x - 7 } { x ^ { 2 } - 4 x - 21 }$ y$g ( x ) = \dfrac { 2 x ^ { 2 } + 5 x - 3 } { 49 - x ^ { 2 } }$, encontrar$( f / g ) ( x )$ y determinar las restricciones.

Solución

$\begin{aligned} ( f / g ) ( x ) & = f ( x ) \quad \div g ( x ) \\ & = \dfrac { 2 x ^ { 2 } + 13 x - 7 } { x ^ { 2 } - 4 x - 21 } \div \dfrac { 2 x ^ { 2 } + 5 x - 3 } { 49 - x ^ { 2 } } \\ & = \dfrac { 2 x ^ { 2 } + 13 x - 7 } { x ^ { 2 } - 4 x - 21 } \cdot \dfrac { 49 - x ^ { 2 } } { 2 x ^ { 2 } + 5 x - 3 } \quad\quad\quad\color{Cerulean}{Multiply\:by\:the\:reciprocal} \\ & = \dfrac { ( 2 x - 1 ) ( x + 7 ) } { ( x + 3 ) ( x - 7 ) } \cdot \dfrac { ( 7 + x ) ( 7 - x ) } { ( 2 x - 1 ) ( x + 3 ) } \quad\color{Cerulean}{Factor.} \\ & = \dfrac { \cancel{(2x-1)}(x+7)(7+x)(-1)\cancel{(x-7)} } {(x+3)\cancel{(x-7)}\cancel{(2x-1)}(x+3) } \:\:\:\color{Cerulean}{Cancel.}\\ & = - \dfrac { ( x + 7 ) ^ { 2 } } { ( x + 3 ) ^ { 2 } } \end{aligned}$

En este caso, el dominio de$f$ consiste en todos los números reales excepto$−3$ y$7$, y el dominio de$g$ consiste en todos los números reales excepto$7$ y$−7$. Además, el recíproco de$g(x)$ tiene una restricción de$−3$ y$\dfrac{1}{2}$. Por lo tanto, el dominio de este cociente consiste en todos los números reales excepto$−3, \dfrac{1}{2}$, y$±7$.

Respuesta:

$( f / g ) ( x ) = - \dfrac { ( x + 7 ) ^ { 2 } } { ( x + 3 ) ^ { 2 } }$, donde$x \neq - 3 , \dfrac { 1 } { 2 } , \pm 7$

Recordemos que las operaciones de multiplicación y división deben realizarse de izquierda a derecha.

Ejemplo$\PageIndex{9}$:

Simplificar:$\dfrac { 4 x ^ { 2 } - 1 } { 6 x ^ { 2 } + 3 x } \div \dfrac { 2 x + 1 } { x ^ { 2 } + 2 x + 1 } \cdot \dfrac { 27 x ^ { 4 } } { 2 x ^ { 2 } + x - 1 }$ (Supongamos que todos los denominadores son distintos de cero.)

Solución

Empezar sustituyendo el factor que se va a dividir por la multiplicación de su recíproco.

$\begin{array} { l } { \dfrac { 4 x ^ { 2 } - 1 } { 6 x ^ { 2 } + 3 x } \color{Cerulean}{\div \dfrac { 2 x + 1 } { x ^ { 2 } + 2 x + 1 }}\color{black}{ \cdot} \dfrac { 27 x ^ { 4 } } { 2 x ^ { 2 } + x - 1 } } \\ { = \dfrac { 4 x ^ { 2 } - 1 } { 6 x ^ { 2 } + 3 x } \cdot \dfrac { x ^ { 2 } + 2 x + 1 } { 2 x + 1 } \cdot \dfrac { 27 x ^ { 4 } } { 2 x ^ { 2 } + x - 1 } } \\ { = \dfrac { ( 2 x + 1 ) ( 2 x - 1 ) } { 3 x ( 2 x + 1 ) } \cdot \dfrac { ( x + 1 ) ( x + 1 ) } { ( 2 x + 1 ) } \cdot \dfrac { 27 x ^ { 3 } } { ( 2 x - 1 ) ( x + 1 ) } } \\ = \dfrac{\cancel{(2x+1)}\cancel{(2x-1)}\cancel{(x+1)}(x+1)\cdot \stackrel{9}{\cancel{27}} \stackrel{x^{3}}{\cancel{x^{4}}}}{\cancel{3}\cancel{ x}\cancel{ (2x+1)}(2x+1)\cancel{(2x-1)}\cancel{(x+1)}} \\ { = \dfrac { 9 x ^ { 3 } ( x + 1 ) } { ( 2 x + 1 ) } } \end{array}$

Respuesta:

$\dfrac { 9 x ^ { 3 } ( x + 1 ) } { ( 2 x + 1 ) }$

Ejercicio$\PageIndex{3}$

Dado$f ( x ) = \dfrac { 2 x + 5 } { 3 x ^ { 2 } + 14 x - 5 }$ y$g ( x ) = \dfrac { 6 x ^ { 2 } + 13 x - 5 } { x + 5 }$, calcular$( f / g ) ( x )$ y determinar las restricciones.

Contestar

$( f / g ) ( x ) = \dfrac { 1 } { ( 3 x - 1 ) ^ { 2 } }$, donde$x \neq - 5 , - \dfrac { 5 } { 2 } , \dfrac { 1 } { 3 }$

www.youtube.com/V/UCPL1zqivwe

Si una función de costo$C$ representa el costo de producir$x$ unidades, entonces el costo promedio ³¹$\overline{C}$ es el costo dividido por el número de unidades producidas.

$\overline { C } ( x ) = \dfrac { C ( x ) } { x }$

Ejemplo$\PageIndex{10}$:

Un fabricante ha determinado que el costo en dólares de producir suéteres viene dado por\ 9C (x) = 0.01 x ^ {2} - 3 x + 1200\), donde$x$ representa el número de suéteres producidos diariamente. Determinar el costo promedio de producción$100, 200$, y$300$ suéteres por día.

Solución

Configure una función que represente el costo promedio.

$\overline { C } ( x ) = \dfrac { C ( x ) } { x } = \dfrac { 0.01 x ^ { 2 } - 3 x + 1200 } { x }$

A continuación, calcular$\overline { C } (100)$,$\overline { C } (200)$, y$\overline { C } (300)$.

$\begin{array} { l } { \overline { C } ( 100 ) = \dfrac { 0.01 ( \color{OliveGreen}{100}\color{black}{ )} ^ { 2 } - 3 (\color{OliveGreen}{ 100}\color{black}{ )} + 1200 } { (\color{OliveGreen}{100}\color{black}{ )} } = \dfrac { 100 - 300 + 1200 } { 100 } = \dfrac { 1000 } { 100 } = 10.00 } \\ { \overline { C } ( 200 ) = \dfrac { 0.01 ( \color{OliveGreen}{200}\color{black}{ )} ^ { 2 } - 3 ( \color{OliveGreen}{200}\color{black}{ )} + 1200 } { ( \color{OliveGreen}{200} ) } = \dfrac { 400 - 600 + 1200 } { 200 } = \dfrac { 1000 } { 200 } = 5.00 } \\ { \overline { C } ( 300 ) = \dfrac { 0.01 ( \color{OliveGreen}{300}\color{black}{ )} ^ { 2 } - 3 ( \color{OliveGreen}{300}\color{black}{ )} + 1200 } { ( \color{OliveGreen}{300}\color{black}{ )} } = \dfrac { 900 - 900 + 1200 } { 300 } = \dfrac { 1200 } { 300 } = 4.00 } \end{array}$

Respuesta:

El costo promedio de producir$100$ suéteres por día es$$10.00$ por jersey. Si se producen 200 suéteres, el costo promedio por suéter es$$5.00$. Si$300$ se producen, el costo promedio por jersey es$$4.00$.

Claves para llevar

Simplificar expresiones racionales es similar a simplificar fracciones. Primero, factorizar el numerador y el denominador y luego cancelar los factores comunes. Las expresiones racionales se simplifican si no hay factores comunes distintos de 1 en el numerador y el denominador.
Las funciones racionales simplificadas son equivalentes para valores en el dominio de la función original. Asegúrese de indicar las restricciones a menos que el problema indique que se supone que los denominadores son distintos de cero.
Después de multiplicar expresiones racionales, factorizar tanto el numerador como el denominador y luego cancelar los factores comunes. Tomar nota de las restricciones al dominio. Los valores que dan un valor de$0$ en el denominador para todas las expresiones son las restricciones.
Para dividir expresiones racionales, multiplique el numerador por el recíproco del divisor.
Las restricciones al dominio de un producto consisten en las restricciones al dominio de cada factor.

Ejercicio$\PageIndex{4}$

Simplifica la función y establece su dominio usando notación de intervalos.

$f ( x ) = \dfrac { 25 x ^ { 9 } } { 5 x ^ { 5 } }$
$f ( x ) = \dfrac { 64 x ^ { 8 } } { 16 x ^ { 3 } }$
$f ( x ) = \dfrac { x ^ { 2 } - 64 } { x ^ { 2 } + 16 x + 64 }$
$f ( x ) = \dfrac { x ^ { 2 } + x - 20 } { x ^ { 2 } - 25 }$
$g ( x ) = \dfrac { 9 - 4 x ^ { 2 } } { 2 x ^ { 2 } - 5 x + 3 }$
$g ( x ) = \dfrac { x - 3 x ^ { 2 } } { 9 x ^ { 2 } - 6 x + 1 }$
$g ( x ) = \dfrac { 2 x ^ { 2 } - 8 x - 42 } { 2 x ^ { 2 } + 5 x - 3 }$
$g ( x ) = \dfrac { 6 x ^ { 2 } + 5 x - 4 } { 3 x ^ { 2 } + x - 4 }$
$h ( x ) = \dfrac { x ^ { 3 } + x ^ { 2 } - x - 1 } { x ^ { 2 } + 2 x + 1 }$
$h ( x ) = \dfrac { 2 x ^ { 3 } - 5 x ^ { 2 } - 8 x + 20 } { 2 x ^ { 2 } - 9 x + 10 }$

Contestar

1. $f ( x ) = 5 x ^ { 4 }$; Dominio:$( - \infty , 0 ) \cup ( 0 , \infty )$

3. $f ( x ) = \dfrac { x - 8 } { x + 8 }$; Dominio:$( - \infty , - 8 ) \cup ( - 8 , \infty )$

5. $g ( x ) = - \dfrac { 2 x + 3 } { x - 1 }$; Dominio:$( - \infty , 1 ) \cup \left( 1 , \dfrac { 3 } { 2 } \right) \cup \left( \dfrac { 3 } { 2 } , \infty \right)$

7. $g ( x ) = \dfrac { 2 ( x - 7 ) } { 2 x - 1 }$; Dominio:$( - \infty , - 3 ) \cup \left( - 3 , \dfrac { 1 } { 2 } \right) \cup \left( \dfrac { 1 } { 2 } , \infty \right)$

9. $h ( x ) = x - 1$; Dominio:$( - \infty , - 1 ) \cup ( - 1 , \infty )$

Ejercicio$\PageIndex{5}$

Indicar las restricciones y simplificar las expresiones racionales dadas.

$\dfrac { 66 x ( 2 x - 5 ) } { 18 x ^ { 3 } ( 2 x - 5 ) ^ { 2 } }$
$\dfrac { 26 x ^ { 4 } ( 5 x + 2 ) ^ { 3 } } { 20 x ^ { 5 } ( 5 x + 2 ) }$
$\dfrac { x ^ { 2 } + 5 x + 6 } { x ^ { 2 } - 5 x - 14 }$
$\dfrac { x ^ { 2 } - 8 x + 12 } { x ^ { 2 } - 2 x - 24 }$
$\dfrac { 1 - x ^ { 2 } } { 5 x ^ { 2 } + x - 6 }$
$\dfrac { 4 - 9 x ^ { 2 } } { 3 x ^ { 2 } - 8 x + 4 }$
$\dfrac { 4 x ^ { 2 } + 15 x + 9 } { 9 - x ^ { 2 } }$
$\dfrac { 6 x ^ { 2 } + 13 x - 5 } { 25 - 4 x ^ { 2 } }$
$\dfrac { x ^ { 2 } - 5 x + 4 } { x ^ { 3 } - x ^ { 2 } - 16 x + 16 }$
$\dfrac { x ^ { 4 } + 4 x ^ { 2 } } { x ^ { 3 } + 3 x ^ { 2 } + 4 x + 12 }$

Contestar

1. $\dfrac { 11 } { 3 x ^ { 2 } ( 2 x - 5 ) } ; x \neq 0 , \dfrac { 5 } { 2 }$

3. $\dfrac { x + 3 } { x - 7 } ; x \neq - 2,7$

5. $- \dfrac { x + 1 } { 5 x + 6 } ; x \neq - \dfrac { 6 } { 5 } , 1$

7. $- \dfrac { 4 x + 3 } { 3 - x } ; x \neq \pm 3$

9. $\dfrac { 1 } { x + 4 } ; x \neq 1 , \pm 4$

Ejercicio$\PageIndex{6}$

Simplificar las expresiones racionales dadas. Supongamos que todas las expresiones variables en el denominador son distintas de cero.

$\dfrac { 50 a b ^ { 3 } ( a + b ) ^ { 2 } } { 200 a ^ { 2 } b ^ { 3 } ( a + b ) ^ { 3 } }$
$\dfrac { 36 a ^ { 5 } b ^ { 7 } ( a - b ) ^ { 2 } } { 9 a ^ { 3 } b ( a - b ) }$
$\dfrac { a ^ { 2 } - b ^ { 2 } } { a ^ { 2 } + 2 a b + b ^ { 2 } }$
$\dfrac { a ^ { 2 } - 2 a b + b ^ { 2 } } { a ^ { 2 } - b ^ { 2 } }$
$\dfrac { 6 x ^ { 2 } - x y } { 6 x ^ { 2 } - 7 x y + y ^ { 2 } }$
$\dfrac { y - x } { 2 x ^ { 3 } - 4 x ^ { 2 } y + 2 x y ^ { 2 } }$
$\dfrac { x ^ { 2 } y ^ { 2 } - 2 x y ^ { 3 } } { x ^ { 2 } y ^ { 2 } - x y ^ { 3 } - 2 y ^ { 4 } }$
$\dfrac { x ^ { 4 } y - x ^ { 2 } y ^ { 3 } } { x ^ { 3 } y + 2 x ^ { 2 } y ^ { 2 } + x y ^ { 3 } }$
$\dfrac { x ^ { 3 } - x ^ { 2 } y + x y ^ { 2 } - y ^ { 3 } } { x ^ { 4 } - y ^ { 4 } }$
$\dfrac { y ^ { 4 } - x ^ { 4 } } { x ^ { 3 } + x ^ { 2 } y + x y ^ { 2 } + y ^ { 3 } }$
$\dfrac { a ^ { 2 } - ( b + c ) ^ { 2 } } { ( a + b ) ^ { 2 } - c ^ { 2 } }$
$\dfrac { ( a + b ) ^ { 2 } - c ^ { 2 } } { ( a + c ) ^ { 2 } - b ^ { 2 } }$
$\dfrac { x ^ { 3 } + y ^ { 3 } } { x ^ { 2 } + 2 x y + y ^ { 2 } }$
$\dfrac { x ^ { 3 } y + x ^ { 2 } y ^ { 2 } + x y ^ { 3 } } { x ^ { 3 } - y ^ { 3 } }$

Contestar

1. $\dfrac { 1 } { 4 a ( a + b ) }$

3. $\dfrac { a - b } { a + b }$

5. $\dfrac { x } { x - y }$

7. $\dfrac { x } { x + y }$

9. $\dfrac { 1 } { x + y }$

11. $\dfrac { a - b - c } { a + b - c }$

13. $\dfrac { x ^ { 2 } - x y + y ^ { 2 } } { x + y }$

Ejercicio$\PageIndex{7}$

Dada la función, simplificar la expresión racional.

Dado$f ( x ) = x ^ { 2 } - 8$, simplificar$\dfrac { f ( x ) - f ( 5 ) } { x - 5 }$.
Dado$f ( x ) = x ^ { 2 } + 4 x - 1$, simplificar$\dfrac { f ( x ) - f ( 2 ) } { x - 2 }$.
Dado$g ( x ) = x ^ { 2 } - 3 x + 1$, simplificar$\dfrac { g ( x ) - g ( - 1 ) } { x + 1 }$.
Dado$g ( x ) = x ^ { 2 } - 2 x$, simplificar$\dfrac { g ( x ) - g ( - 4 ) } { x + 4 }$.
Dado$f ( x ) = 4 x ^ { 2 } + 6 x + 1$, simplificar$\dfrac { f ( x ) - f \left( \dfrac { 1 } { 2 } \right) } { 2 x - 1 }$.
Dado$f ( x ) = 9 x ^ { 2 } + 1$, simplificar$\dfrac { f ( x ) - f \left( - \dfrac { 1 } { 3 } \right) } { 3 x + 1 }$.

Contestar

1. $x+5$, donde$x \neq 5$

3. $x-4$, donde$x \neg -1$

5. $2(x+2)$, donde$x \neq \dfrac{1}{2}$

Ejercicio$\PageIndex{8}$

Para la función dada, simplificar el cociente de diferencia$\dfrac { f ( x + h ) - f ( x ) } { h }$, donde$h\neq 0$.

$f ( x ) = 5 x - 3$
$f ( x ) = 3 - 2 x$
$f ( x ) = x ^ { 2 } - 3$
$f ( x ) = x ^ { 2 } + 8 x$
$f ( x ) = x ^ { 2 } - x + 5$
$f ( x ) = 4 x ^ { 2 } + 3 x - 2$
$f ( x ) = a x ^ { 2 } + b x + c$
$f ( x ) = a x ^ { 2 } + b x$
$f ( x ) = x ^ { 3 } + 1$
$f ( x ) = x ^ { 3 } - x + 2$

Contestar

1. $5$

3. $2x+h$

5. $2x-1+h$

7. $2ax+b+ah$

9. $3 x ^ { 2 } + 3 x h + h ^ { 2 }$

Ejercicio$\PageIndex{9}$

Simplifique el producto$f \cdot g$ y establezca su dominio usando la notación de intervalos.

$f ( x ) = \dfrac { 52 x ^ { 4 } } { ( x - 2 ) ^ { 2 } } , g ( x ) = \dfrac { ( x - 2 ) ^ { 3 } } { 12 x ^ { 5 } }$
$f ( x ) = \dfrac { 46 ( 2 x - 1 ) ^ { 3 } } { 15 x ^ { 6 } } , g ( x ) = \dfrac { 25 x ^ { 3 } } { 23 ( 2 x - 1 ) }$
$f ( x ) = \dfrac { 10 x ^ { 3 } } { x ^ { 2 } + 4 x + 4 } , g ( x ) = \dfrac { x ^ { 2 } - 4 } { 50 x ^ { 4 } }$
$f ( x ) = \dfrac { 25 - x ^ { 2 } } { 46 x ^ { 5 } } , g ( x ) = \dfrac { 12 x ^ { 3 } } { x ^ { 2 } + 10 x + 25 }$
$f ( x ) = \dfrac { 5 - 3 x } { x ^ { 2 } - 10 x + 25 } , g ( x ) = \dfrac { x ^ { 2 } - 6 x + 5 } { 3 x ^ { 2 } - 8 x + 5 }$
$f ( x ) = \dfrac { 1 - 4 x ^ { 2 } } { 6 x ^ { 2 } + 3 x } , g ( x ) = \dfrac { 12 x ^ { 2 } } { 4 x ^ { 2 } - 4 x + 1 }$

Contestar

1. $( f \cdot g ) ( x ) = \dfrac { 13 ( x - 2 ) } { 3 x }$; Dominio:$( - \infty , 0 ) \cup ( 0,2 ) \cup ( 2 , \infty )$

3. $( f \cdot g ) ( x ) = \dfrac { x - 2 } { 5 x ( x + 2 ) }$; Dominio:$( - \infty , - 2 ) \cup ( - 2,0 ) \cup ( 0 , \infty )$

5. $( f \cdot g ) ( x ) = - \dfrac { 1 } { x - 5 }$; Dominio:$( - \infty , 1 ) \cup \left( 1 , \dfrac { 5 } { 3 } \right) \cup \left( \dfrac { 5 } { 3 } , 5 \right) \cup ( 5 , \infty )$

Ejercicio$\PageIndex{10}$

Simplifica el cociente$f/g$ y establece su dominio usando notación de intervalos.

$f ( x ) = \dfrac { 12 x ^ { 3 } } { 5 ( 5 x - 1 ) ^ { 3 } } , g ( x ) = \dfrac { 6 x ^ { 2 } } { 25 ( 5 x - 1 ) ^ { 4 } }$
$f ( x ) = \dfrac { 7 x ^ { 2 } ( x + 9 ) } { ( x - 8 ) ^ { 2 } } , g ( x ) = \dfrac { 49 x ^ { 3 } ( x + 9 ) } { ( x - 8 ) ^ { 4 } }$
$f ( x ) = \dfrac { 25 x ^ { 2 } - 1 } { 3 x ^ { 2 } - 15 x } , g ( x ) = \dfrac { 25 x ^ { 2 } + 10 x + 1 } { x ^ { 3 } - 5 x ^ { 2 } }$
$f ( x ) = \dfrac { x ^ { 2 } - x - 6 } { 2 x ^ { 2 } + 13 x + 15 } , g ( x ) = \dfrac { x ^ { 2 } - 6 x + 9 } { 4 x ^ { 2 } + 12 x + 9 }$
$f ( x ) = \dfrac { x ^ { 2 } - 64 } { x ^ { 2 } } , g ( x ) = 2 x ^ { 2 } + 19 x + 24$
$f ( x ) = 2 x ^ { 2 } + 11 x - 6 , g ( x ) = 36 - x ^ { 2 }$

Contestar

1. $( f / g ) ( x ) = 10 x ( 5 x - 1 )$; Dominio:$( - \infty , 0 ) \cup \left( 0 , \dfrac { 1 } { 5 } \right) \cup \left( \dfrac { 1 } { 5 } , \infty \right)$

3. $( f / g ) ( x ) = \dfrac { x ( 5 x - 1 ) } { 2 ( 5 x + 1 ) }$; Dominio:$( - \infty , 0 ) \cup \left( 0 , \dfrac { 1 } { 5 } \right) \cup \left( \dfrac { 1 } { 5 } , \infty \right)$

5. $( f / g ) ( x ) = \dfrac { x - 8 } { x ^ { 2 } ( 2 x + 3 ) }$; Dominio:$( - \infty , - 8 ) \cup \left( - 8 , - \dfrac { 3 } { 2 } \right) \cup \left( - \dfrac { 3 } { 2 } , 0 \right) \cup ( 0 , \infty )$

Ejercicio$\PageIndex{11}$

Multiplicar o dividir como se indica, indicar las restricciones y simplificar.

$\dfrac { 14 ( x + 12 ) ^ { 2 } } { 5 x ^ { 3 } } \cdot \dfrac { 45 x ^ { 4 } } { 2 ( x + 12 ) ^ { 3 } }$
$\dfrac { 27 x ^ { 6 } } { 20 ( x - 7 ) ^ { 3 } } \cdot \dfrac { ( x - 7 ) ^ { 5 } } { 54 x ^ { 7 } }$
$\dfrac { x ^ { 2 } - 64 } { 36 x ^ { 4 } } \cdot \dfrac { 12 x ^ { 3 } } { x ^ { 2 } + 4 x - 32 }$
$\dfrac { 50 x ^ { 5 } } { x ^ { 2 } + 6 x - 27 } \cdot \dfrac { x ^ { 2 } - 81 } { 125 x ^ { 3 } }$
$\dfrac { 2 x ^ { 2 } + 7 x + 5 } { 3 x ^ { 2 } } \cdot \dfrac { 15 x ^ { 3 } - 30 x ^ { 2 } } { 2 x ^ { 2 } + x - 10 }$
$\dfrac { 3 x ^ { 2 } + 14 x - 5 } { 2 x ^ { 2 } + 11 x + 5 } \cdot \dfrac { 4 x ^ { 2 } + 4 x + 1 } { 6 x ^ { 2 } + x - 1 }$
$\dfrac { x ^ { 2 } + 4 x - 21 } { 5 x ^ { 2 } + 10 x } \div \dfrac { x ^ { 2 } - 6 x + 9 } { x ^ { 2 } + 9 x + 14 }$
$\dfrac { x ^ { 2 } - 49 } { 9 x ^ { 2 } - 24 x + 16 } \div \dfrac { 2 x ^ { 2 } - 13 x - 7 } { 6 x ^ { 2 } - 5 x - 4 }$
$\dfrac { 5 x ^ { 2 } + x - 6 } { 4 x ^ { 2 } - 7 x - 15 } \div \dfrac { 1 - x ^ { 2 } } { 4 x ^ { 2 } + 9 x + 5 }$
$\dfrac { 6 x ^ { 2 } - 8 x - 8 } { 4 - 9 x ^ { 2 } } \div \dfrac { 3 x ^ { 2 } - 4 x - 4 } { 9 x ^ { 2 } + 12 x + 4 }$
$\dfrac { x ^ { 2 } + 4 x - 12 } { x ^ { 2 } - 2 x - 15 } \div \dfrac { 2 x ^ { 2 } - 13 x + 18 } { 6 x ^ { 2 } - 31 x + 5 }$
$\dfrac { 8 x ^ { 2 } + x - 9 } { 25 x ^ { 2 } - 1 } \div \dfrac { 2 x ^ { 2 } - x - 1 } { 10 x ^ { 2 } - 3 x - 1 }$

Contestar

1. $\dfrac { 63 x } { x + 12 } ; x \neq - 12,0$

3. $\dfrac { x - 8 } { 3 x ( x - 4 ) } ; x \neq - 8,0,4$

5. $5 ( x + 1 ) ; x \neq - \dfrac { 5 } { 2 } , 0,2$

7. $\dfrac { ( x + 7 ) ^ { 2 } } { 5 x ( x - 3 ) } ; x \neq - 7 , - 2,0,3$

9. $- \dfrac { 5 x + 6 } { x - 3 } ; x \neq - \dfrac { 5 } { 4 } , - 1,1,3$

11. $\dfrac { ( x + 6 ) ( 6 x - 1 ) } { ( x + 3 ) ( 2 x - 9 ) } ; x \neq - 3 , \dfrac { 1 } { 6 } , 2 , \dfrac { 9 } { 2 } , 5$

Ejercicio$\PageIndex{12}$

Realizar las operaciones y simplificar. Supongamos que todas las expresiones variables en el denominador son distintas de cero.

$\dfrac { 1 } { 12 a b } \cdot \dfrac { 50 a ^ { 2 } ( a - b ) ^ { 2 } } { a ^ { 2 } - b ^ { 2 } } \cdot \dfrac { 6 b } { a ( a - b ) }$
$\dfrac { b ^ { 2 } - a ^ { 2 } } { ( a - b ) ^ { 2 } } \cdot \dfrac { 12 a ( a - b ) } { 36 a ^ { 2 } b } \cdot \dfrac { 9 a b ( a - b ) } { a + b }$
$\dfrac { x ^ { 3 } + y ^ { 3 } } { 5 x y } \cdot \dfrac { x ^ { 2 } - y ^ { 2 } } { x ^ { 2 } - 2 x y + y ^ { 2 } } \cdot \dfrac { 25 x ^ { 2 } y } { ( y + x ) ^ { 2 } }$
$\dfrac { 3 x y ^ { 2 } } { ( 2 y + x ) ^ { 2 } } \cdot \dfrac { 2 x ^ { 2 } + 5 x y + 2 y ^ { 2 } } { 9 x ^ { 2 } } \cdot \dfrac { x ^ { 3 } + 8 y ^ { 3 } } { 6 x y ^ { 2 } + 3 y ^ { 3 } }$
$\dfrac { 2 x + 5 } { x - 3 } \cdot \dfrac { x ^ { 2 } - 9 } { 5 x ^ { 4 } } \div \dfrac { 2 x ^ { 2 } + 15 x + 25 } { 25 x ^ { 5 } }$
$\dfrac { 5 x ^ { 2 } - 15 x } { 9 x ^ { 2 } - 4 } \cdot \dfrac { 3 x - 2 } { 20 x ^ { 3 } } \div \dfrac { x - 3 } { 3 x ^ { 2 } - x - 2 }$
$\dfrac { x ^ { 2 } + 5 x - 50 } { x ^ { 2 } + 5 x - 14 } \div \dfrac { x ^ { 2 } - 25 } { x ^ { 2 } - 49 } \cdot \dfrac { x - 2 } { x ^ { 2 } + 3 x - 70 }$
$\dfrac { x ^ { 2 } - x - 56 } { 4 x ^ { 2 } - 4 x - 3 } \div \dfrac { 2 x ^ { 2 } + 11 x - 21 } { 25 - 9 x ^ { 2 } } \cdot \dfrac { 4 x ^ { 2 } - 12 x + 9 } { 3 x ^ { 2 } - 19 x - 40 }$
$\dfrac { 20 x ^ { 2 } - 8 x - 1 } { 6 x ^ { 2 } + 13 x + 6 } \div \dfrac { 1 - 100 x ^ { 2 } } { 3 x ^ { 2 } - x - 2 } \cdot \dfrac { 10 x - 1 } { 2 x ^ { 2 } - 3 x + 1 }$
$\dfrac { 12 x ^ { 2 } - 13 x + 1 } { x ^ { 2 } + 18 x + 81 } \div \left( 144 x ^ { 2 } - 1 \right) \cdot \dfrac { x ^ { 2 } + 14 x + 45 } { 12 x ^ { 2 } - 11 x - 1 }$
Un fabricante ha determinado que el costo en dólares de producir bicicletas viene dado por$C (x) = 0.5x^{ 2} − x + 6200$, donde$x$ representa el número de bicicletas producidas semanalmente. Determinar el costo promedio de producción$50, 100$, y$150$ bicicletas por semana.
El costo en dólares de producir accesorios de iluminación personalizados viene dado por la función$C (x) = x^{2} − 20x + 1200$, donde$x$ representa el número de accesorios producidos en una semana. Determinar el costo promedio por unidad si$20, 40$, y$50$ las unidades se producen en una semana.
Un fabricante ha determinado que el costo en dólares de producir scooters eléctricos viene dado por la función$C (x) = 3x (x − 100) + 32,000$, donde$x$ representa el número de scooters producidos en un mes. Determinar el costo promedio por scooter si$50$ se producen en un mes.
El costo en dólares de producir una pieza moldeada inyectada personalizada viene dada por$C (n) = 1,900 + 0.01n$, donde$n$ representa el número de piezas producidas. Calcule el costo promedio de cada pieza si se piden piezas$2,500$ personalizadas.
El costo en dólares de una limpieza ambiental viene dado por la función$C ( p ) = \dfrac { 25,000 p } { 1 - p }$, donde$p$ representa el porcentaje del área a limpiar$(0 ≤ p < 1)$. Utilice la función para determinar el costo de limpieza$50$% de una zona afectada y el costo de limpieza$80$% del área.
El valor de un auto nuevo viene dado por la función$V (t) = 16,500(t + 1)^{−1}$ donde$t$ representa la antigüedad del automóvil en años. Determinar el valor del automóvil cuando tenga$6$ años de antigüedad.

Contestar

1. $\dfrac { 25 } { a + b }$

3. $\dfrac { 5 x \left( x ^ { 2 } - x y + y ^ { 2 } \right) } { x - y }$

5. $\dfrac { 5 x ( x + 3 ) } { x + 5 }$

7. $\dfrac { 1 } { x + 5 }$

9. $- \dfrac { 1 } { 2 x + 3 }$

11. Si se producen$50$ bicicletas, el costo promedio por bicicleta es$$148$. Si$100$ se producen, el costo promedio es$$111$. Si se producen$150$ bicicletas, el costo promedio es$$115.33$.

13. Si se producen$50$ scooters, el costo promedio de cada uno es$$490$.

15. Un$50$% de limpieza costará$$25,000$. Un$80$% de limpieza costará$$100,000$.

Ejercicio$\PageIndex{13}$

Describir las restricciones a la expresión racional$\dfrac { 1 } { x ^ { 2 } - y ^ { 2 } }$. Explique.
Describir las restricciones a la expresión racional$\dfrac { 1 } { x ^ { 2 } + y ^ { 2 } }$. Explique.
Explicar por qué$x = 5$ es una restricción a$\dfrac { 1 } { x + 5 } \div \dfrac { x - 5 } { x }$.
Explicar a un estudiante principiante de álgebra por qué no podemos cancelar$x$ en la expresión racional$\dfrac { x + 2 } { x }$.
Investigar y discutir la importancia del cociente de diferencia. ¿Qué representa y en qué tema aparece?

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

5. La respuesta puede variar

Notas al pie

²⁵ Funciones de la forma$r ( x ) = \dfrac { p ( x ) } { q ( x ) }$, donde$p(x)$ y$q(x)$ son polinomios y$q(x) ≠ 0$.

²⁶ El conjunto de números reales para los que se define la función racional.

²⁷ El conjunto de números reales para los que no se define una función racional.

²⁸ Si se le da un binomio$a-b$, entonces lo contrario es$- ( a - b ) = b - a$.

²⁹ La cantidad matemática$\dfrac { f ( x + h ) - f ( x ) } { h }$, donde$h \neq 0$, que representa la pendiente de una línea secante a través de una función$f$.

³⁰ Línea que cruza dos puntos en la gráfica de una función.

³¹ El costo total dividido por el número de unidades producidas, que puede ser representado por$\overline { C } ( x ) = \dfrac { C ( x ) } { x }$, donde$C(x)$ es una función de costo.