6.4: Funciones cuadráticas y sus gráficas
( \newcommand{\kernel}{\mathrm{null}\,}\)
Objetivos de aprendizaje
- Grafica una parábola.
- Encuentra las intercepciones y el vértice de una parábola.
- Encuentra ely valor máximo y mínimo.
- Encuentra el vértice de una parábola completando el cuadrado.
La gráfica de una función cuadrática
Una función cuadrática es una función polinómica de grado2 que puede escribirse en la forma general,
f(x)=ax2+bx+c
Aquía,b yc representan números reales dondea≠0 .La función de cuadraturaf(x)=x2 es una función cuadrática cuya gráfica sigue.
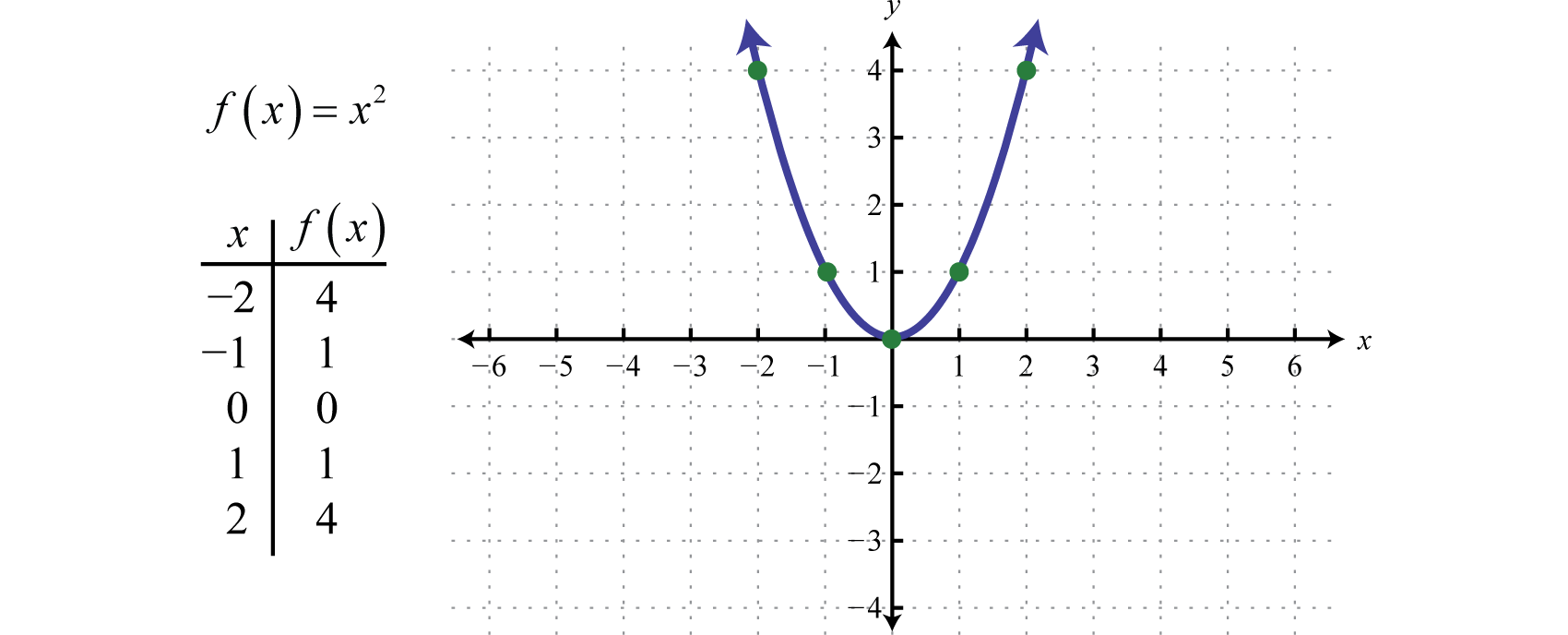
Esta forma curva general se llama parábola 10 y es compartida por las gráficas de todas las funciones cuadráticas. Tenga en cuenta que la gráfica es de hecho una función ya que pasa la prueba de línea vertical. Además, el dominio de esta función consiste en el conjunto de todos los números reales(−∞,∞) y el rango consiste en el conjunto de números no negativos[0,∞).
Al graficar parábolas, queremos incluir ciertos puntos especiales en la gráfica. Ely -intercept es el punto donde la gráfica se cruza con ely eje. Lasx -intercepciones son los puntos donde la gráfica cruza elx eje -eje. El vértice 11 es el punto que define el mínimo o máximo de la gráfica. Por último, la línea de simetría 12 (también llamada eje de simetría 13) es la línea vertical a través del vértice, alrededor de la cual la parábola es simétrica.
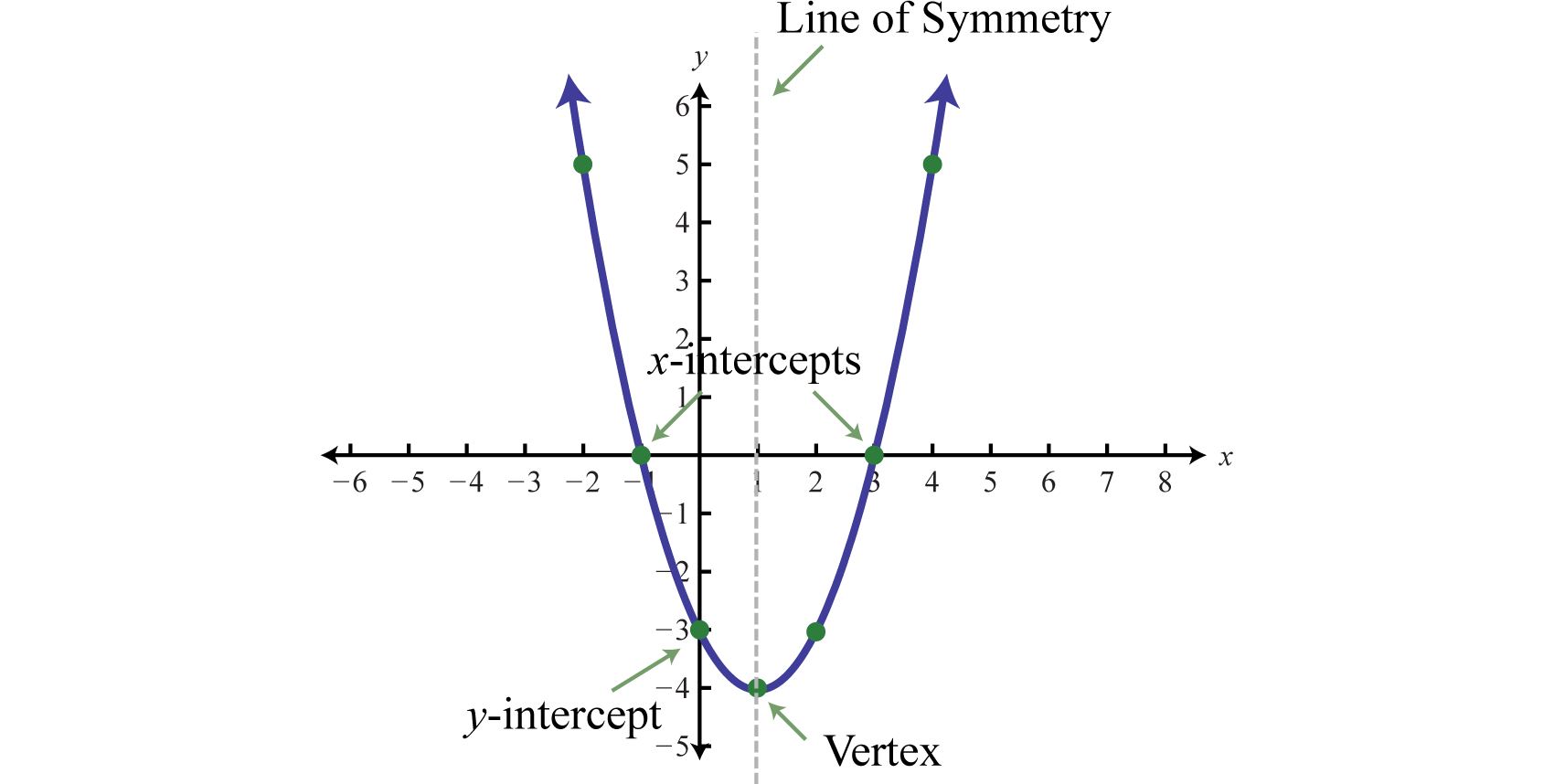
Para cualquier parábola, encontraremos el vértice yy -interceptar. Además, si existen lasx -intercepciones, entonces vamos a querer determinarlas también. Adivinar losx -valores de estos puntos especiales no es práctico; por lo tanto, desarrollaremos técnicas que faciliten encontrarlos. Muchas de estas técnicas serán utilizadas ampliamente a medida que avancemos en nuestro estudio del álgebra.
Dada una función cuadráticaf(x)=ax2+bx+c, encuentra lay -intercepción evaluando la función wherex=0. En generalf(0)=a(0)2+b(0)+c=c,, y tenemos
y−intercept(0,c)
A continuación, recordemos que lasx -intercepciones, si existen, se pueden encontrar configurandof(x)=0. Haciendo esto, tenemosa2+bx+c=0, que tiene soluciones generales dadas por la fórmula cuadrática,\(x=−b±√b2−4ac2a\) .Por lo tanto, lasx -intercepciones tienen esta forma general:
x−intercepts
(−b−√b2−4ac2a,0)y(−b+√b2−4ac2a,0)
Usando el hecho de que una parábola es simétrica, podemos determinar la línea vertical de simetría usando lasx -intercepciones. Para ello, encontramos elx -valor a medio camino entre lasx -intercepciones tomando un promedio de la siguiente manera:
x=(−b−√b2−4ac2a+−b+√b2−4ac2a)÷2=(−b−√b2−4ac−b+√b2−4ac2a)÷(21)=−2b2a⋅12=−b2a
Por lo tanto, la línea de simetría es la línea verticalx=−b2a. Podemos usar la línea de simetría para encontrar el vértice.
LineofsymmetryVertexx=−b2a(−b2a,f(−b2a))
Generalmente tres puntos determinan una parábola. No obstante, en esta sección encontraremos cinco puntos para que podamos obtener una mejor aproximación de la forma general. Los pasos para graficar una parábola se describen en el siguiente ejemplo.
Ejemplo6.4.1:
Gráfica:f(x)=−x2−2x+3.
Solución
Paso 1: Determinar lay -intercepción. Para ello, establecex =0 y encuentraf(0).
f(x)=−x2−2x+3f(0)=−(0)2−2(0)+3=3
Ely -intercepto es(0,3).
Paso 2: Determine lasx -intercepciones si las hubiera. Para ello, establecerf(x)=0 y resolver parax.
f(x)=−x2−2x+3Setf(x)=0.0=−x2−2x+3Multiplybothsidesby−1.0=x2+2x−3Factor.0=(x+3)(x−1)Seteachfactorequaltozero.
x+3=0 or x−1=0x=−3x=1
Aquí dondef(x)=0, obtenemos dos soluciones. De ahí, hay dosx -intercepciones,(−3,0) y(1,0).
Paso 3: Determinar el vértice. Una forma de hacerlo es primero usarx=−b2a para encontrar elx -valor del vértice y luego sustituir este valor en la función para encontrar ely valor -correspondiente. En este ejemplo,a=−1 yb=−2.
x=−b2a=−(−2)2(−1)=2−2=−1
Sustituya−1 en la función original para encontrar ely valor -correspondiente.
f(x)=−x2−2x+3f(−1)=−(−1)2−2(−1)+3=−1+2+3=4
El vértice es(−1,4).
Paso 4: Determinar puntos extra para que tengamos al menos cinco puntos para trazar. Asegurar un buen muestreo a ambos lados de la línea de simetría. En este ejemplo bastará otro punto. Elijax=−2 y encuentre ely -valor correspondiente.
| x | y | Punto | |
|---|---|---|---|
| \ (x\) ">−2 | \ (y\) ">3 | f(−2)=−(−2)2−2(−2)+3=−4+4+3=3 | (−2,3) |
Nuestro quinto punto es(−2,3).
Paso 5: Trazar los puntos y bosquejar la gráfica. Para recapitular, los puntos que hemos encontrado son
y-interceptar:(0,3)
x-intercepta:(−3,0) y(1,0)
Vértice:(−1,4)
Punto extra:(−2,3)
Respuesta:
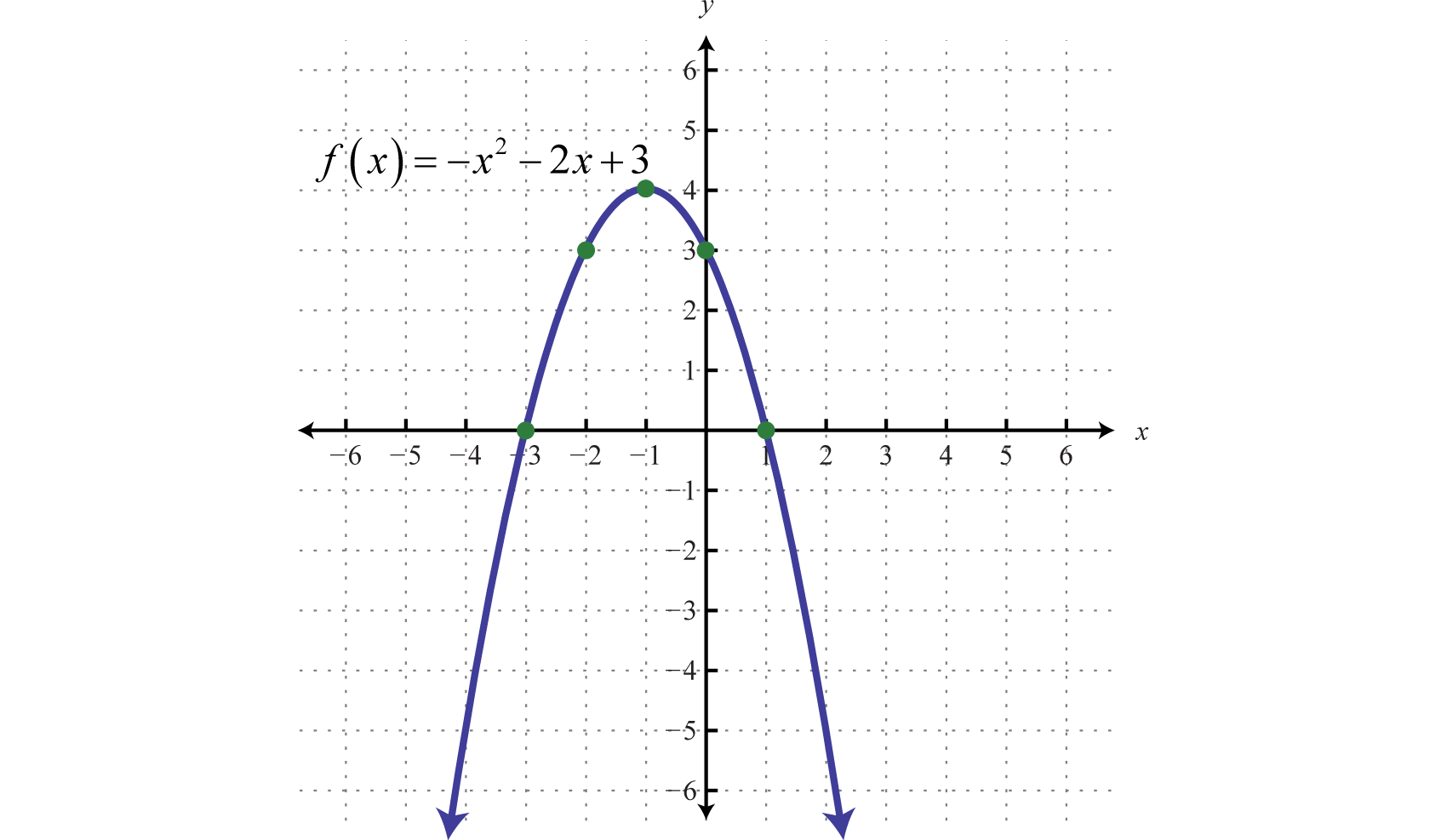
La parábola se abre hacia abajo. En general, utilice el coeficiente principal para determinar si la parábola se abre hacia arriba o hacia abajo. Si el coeficiente inicial es negativo, como en el ejemplo anterior, entonces la parábola se abre hacia abajo. Si el coeficiente principal es positivo, entonces la parábola se abre hacia arriba.
Todas las funciones cuadráticas de la formaf(x)=ax2+bx+c tienen gráficas parabólicas cony -intercepción(0,c). Sin embargo, no todas las parábolas tienenx -intercepciones.
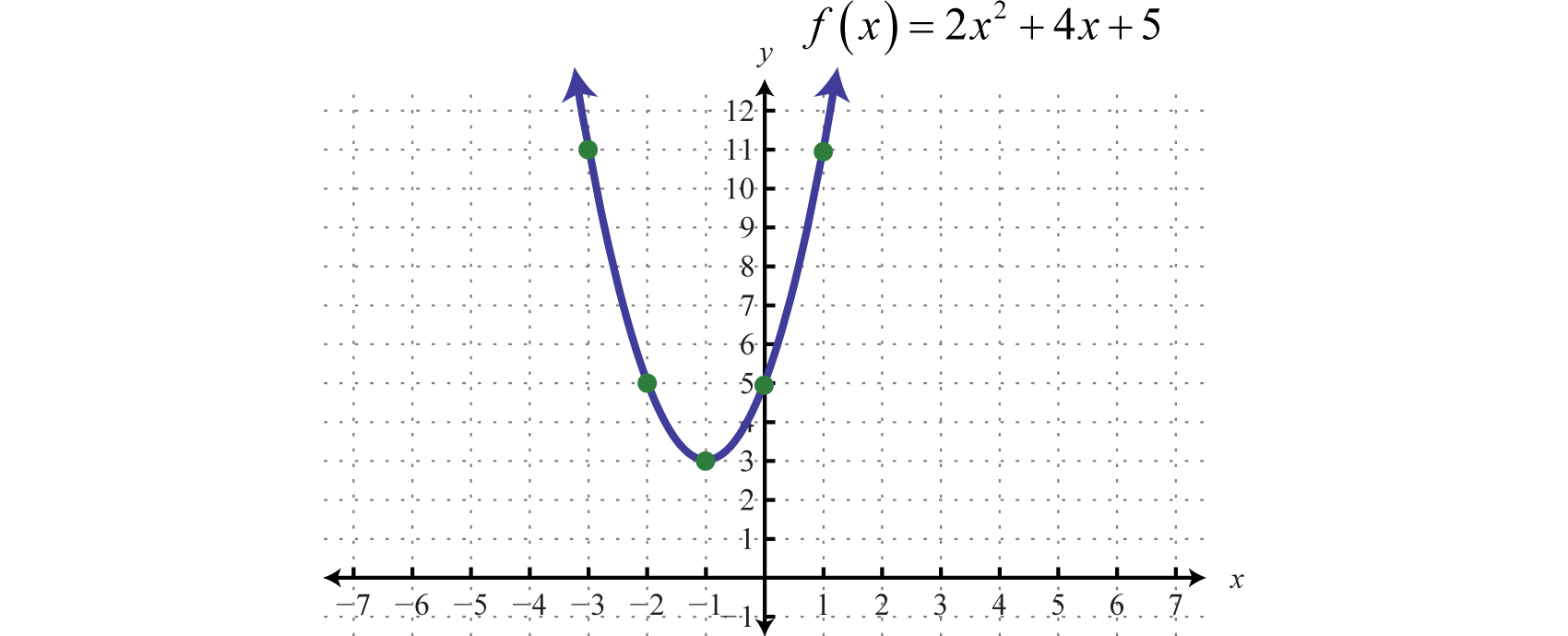
Ejemplo6.4.2:
Gráfica:f(x)=2x2+4x+5.
Solución
Debido a que el coeficiente principal2 es positivo, observamos que la parábola se abre hacia arriba. Aquíc=5 y lay -intercepción es(0,5). Para encontrar lasx -intercepciones, establecerf(x)=0.
f(x)=2x2+4x+50=2x2+4x+5
En este caso,a=2,b=4, yc=5. Utilizar el discriminante para determinar el número y tipo de soluciones.
b2−4ac=(4)2−4(2)(5)=16−40=−24
Dado que el discriminante es negativo, concluimos que no hay soluciones reales. Porque no hay soluciones reales, no hayx -intercepciones. A continuación, determinamos elx -valor del vértice.
x=−b2a=−(4)2(2)=−44=−1
Dado que elx -valor del vértice es−1, sustituya−1 en la ecuación original para encontrar ely -valor correspondiente.
f(x)=2x2+4x+5f(−1)=2(−1)2+4(−1)+5=2−4+5=3
El vértice es(−1,3). Hasta el momento, sólo tenemos dos puntos. Para determinar tres más, elija algunosx -valores a cada lado de la línea de simetría,x=−1. Aquí elegimosx -valores−3,−2, y1.
| x | y | Puntos | |
|---|---|---|---|
| \ (x\) ">−3 | \ (y\) ">11 | f(−3)=2(−3)2+4(−3)+5=18−12+5=11 | (−3,11) |
| \ (x\) ">−2 | \ (y\) ">5 | f(−2)=2(−2)2+4(−2)+5=8−8+5=5 | (−2,5) |
| \ (x\) ">1 | \ (y\) ">11 | f(1)=2(1)2+4(1)+5=2+4+5=11 | (1,11) |
Para resumir, tenemos
y-interceptar:(0,5)
x-intercepta: Ninguno
Vértice:(−1,3)
Puntos extra:(−3,11),(−2,5),(1,11)
Trazar los puntos y bosquejar la gráfica.
Respuesta:
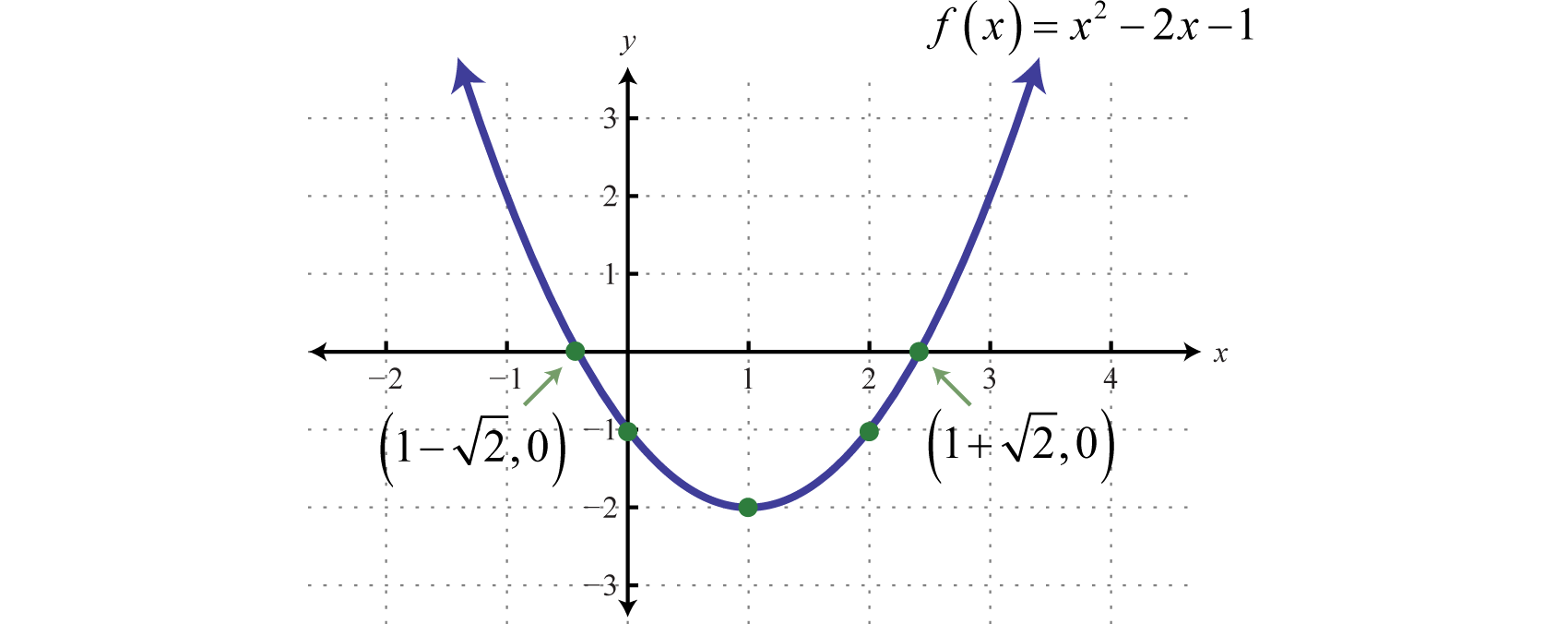
Ejemplo6.4.3:
Gráfica:f(x)=x2−2x−1.
Solución
Ya quea=1, la parábola se abre hacia arriba. Ademásc=−1, así lo es lay -intercepción(0,−1). Para encontrar lasx -intercepciones, establecerf(x)=0.
f(x)=x2−2x−10=x2−2x−1
En este caso, resolver usando la fórmula cuadrática cona=1,b=−2, yc=−1.
x=−b±√b2−4ac2a=−(−2)±√(−2)2−4(1)(−1)2(1)=2±√82=2±2√22=2(1±√2)2=1±√2
Aquí obtenemos dos soluciones reales parax, y así hay dosx -intercepciones:
(1−√2,0) and (1+√2,0)Exactvalues(−0.41,0)(2.41,0)Approximatevalues
Aproximar lasx -intercepciones usando una calculadora nos ayudará a trazar los puntos. No obstante, presentaremos lasx intercepciones exactas en la gráfica. A continuación, encuentra el vértice.
x=−b2a=−(−2)2(1)=22=1
Dado que elx -valor del vértice es1, sustituya en la ecuación original para encontrar ely -valor correspondiente.
y=x2−2x−1=(1)2−2(1)−1=1−2−1=−2
El vértice es(1,−2). Necesitamos un punto más.
| x | y | Punto | |
|---|---|---|---|
| \ (x\) ">2 | \ (y\) ">−1 | f(2)=(2)2−2(2)−1=4−4−1=−1 | (2,−1) |
Para resumir, tenemos
y-intercepta:(0,1)
x-intercepta:(1−√2,0) y(1+√2,0)
Vértice:(1,−2)
Punto extra:(2,−1)
Trazar los puntos y bosquejar la gráfica.
Respuesta:
Ejercicio6.4.1
Gráfica:g(x)=−4x2+12x−9.
- Contestar
-
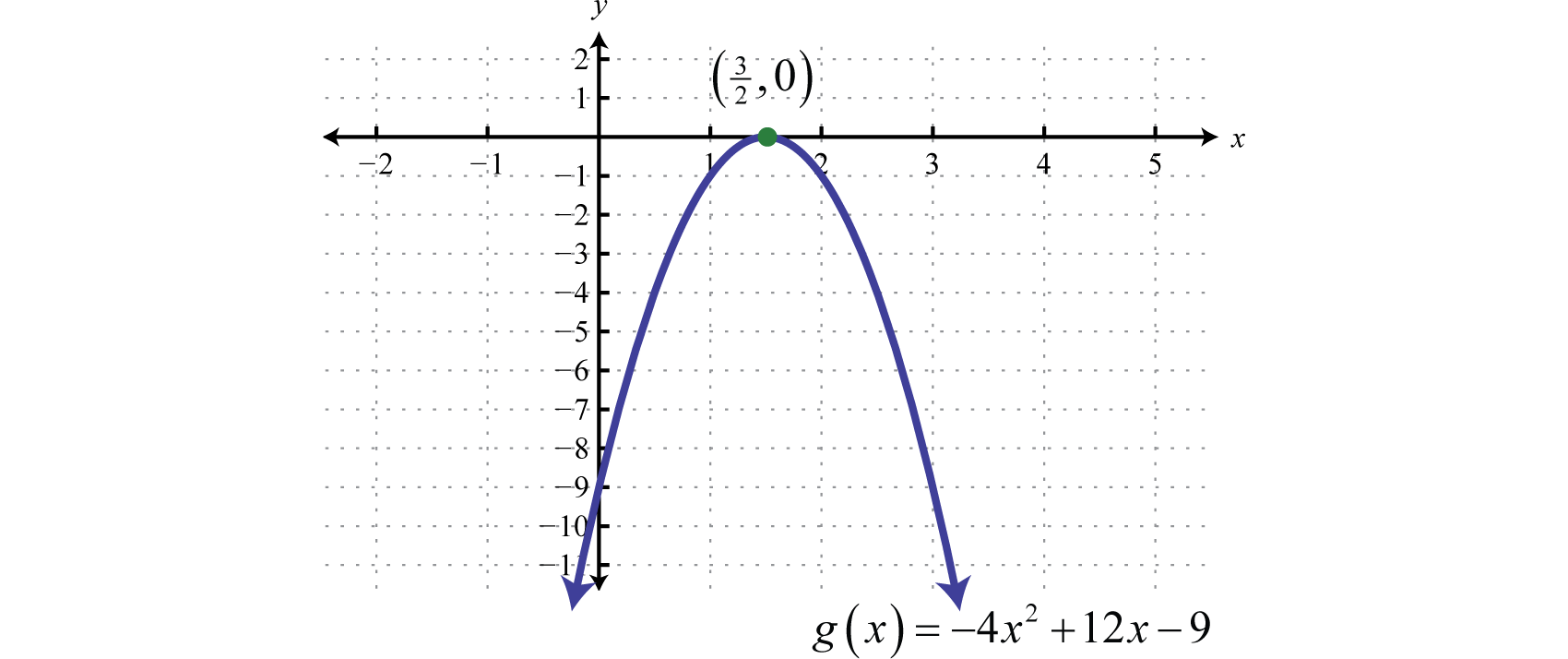
Figura6.4.7 www.youtube.com/V/TQIDXNHN7IK
Encontrar el Máximo o Mínimo
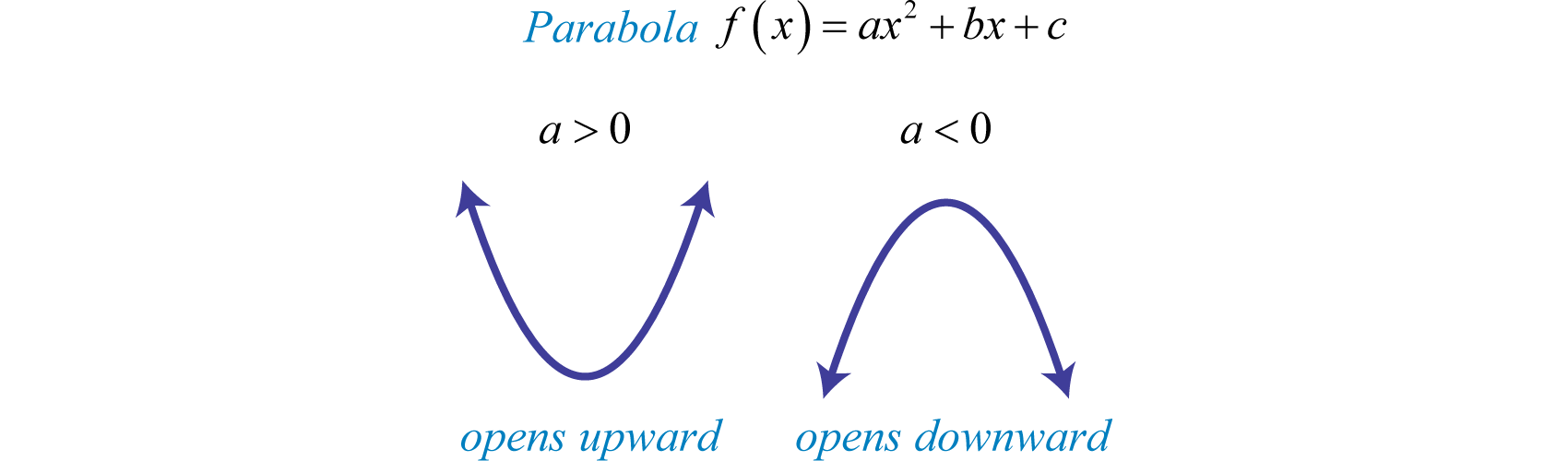
A menudo es útil encontrar los valores máximos y/o mínimos de funciones que modelan aplicaciones de la vida real. Para encontrar estos valores importantes dados una función cuadrática, usamos el vértice. Si el coeficiente iniciala es positivo, entonces la parábola se abre hacia arriba y habrá uny valor mínimo. Si el coeficiente iniciala es negativo, entonces la parábola se abre hacia abajo y habrá uny valor máximo.
Ejemplo6.4.4:
Determinar el máximo o mínimo:y=−4x2+24x−35.
Solución
Ya quea=−4, sabemos que la parábola se abre hacia abajo y habrá uny valor máximo. Para encontrarlo, primero encuentra elx -valor del vértice.
x=−b2ax−valueofthevertex.=−242(−4)Substitutea=−4andb−24.=−24−8Simplify.=3
Elx -valor del vértice es3. Sustituya este valor en la ecuación original para encontrar ely valor -correspondiente.
y=−4x2+24x−35Substitutex=3.=−4(3)2+24(3)−35Simplify.=−36+72−35=1
El vértice es(3,1). Por lo tanto, ely valor máximo es1, que ocurre dondex=3, como se ilustra a continuación:
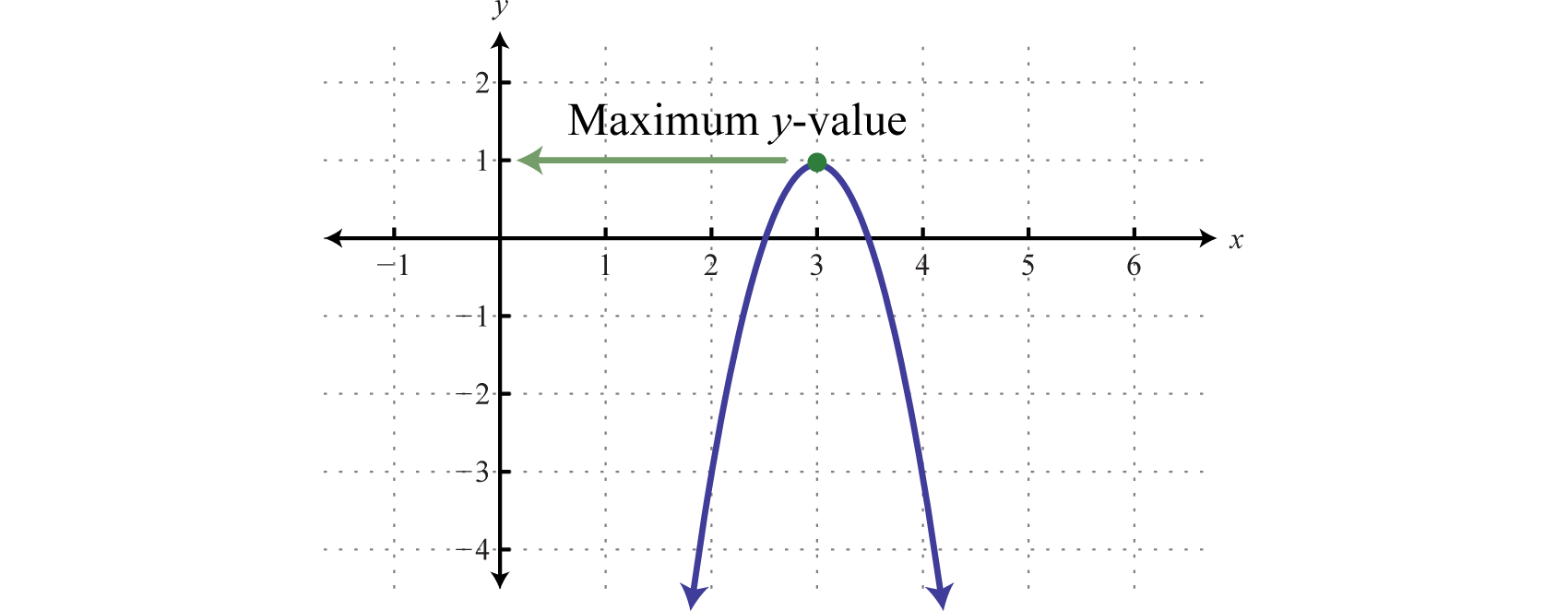
Nota: No se requiere la gráfica para responder a esta pregunta.
Respuesta:
El máximo es1.
Ejemplo6.4.5:
Determinar el máximo o mínimo:y=4x2−32x+62.
Solución
Ya quea=4, la parábola se abre hacia arriba y hay uny valor mínimo. Comience por encontrar elx -valor del vértice.
x=−b2a=−−322(4)Substitutea=4andb=−32.=−−328Simplify.=4
Sustituyax=4 en la ecuación original para encontrar ely valor -correspondiente.
y=4x2−32x+62=4(4)2−32(4)+62=64−128+62=−2
El vértice es(4,−2). Por lo tanto, ely valor mínimo de−2 ocurre dondex=4, como se ilustra a continuación:
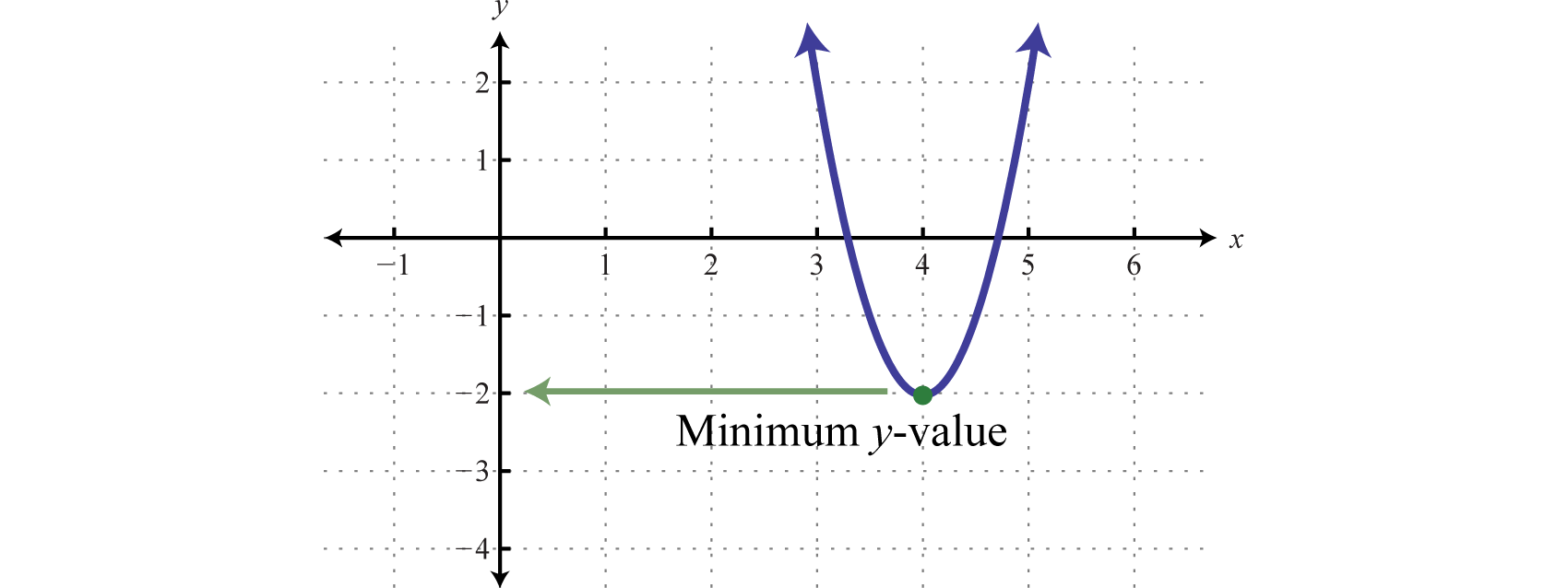
Respuesta:
El mínimo es−2.
Ejemplo6.4.6:
La altura en pies de un proyectil viene dada por la funciónh(t)=−16t2+72t, dondet representa el tiempo en segundos después del lanzamiento. ¿Cuál es la altura máxima que alcanza el proyectil?
Solución
Aquía=−16, y la parábola se abre hacia abajo. Por lo tanto, ely -valor del vértice determina la altura máxima. Comience por encontrar el momento en que se produce el vértice.
t=−b2a=−722(−16)=7232=94
La altura máxima ocurrirá en94 segundos (o214 segundos). Sustituya este tiempo en la función para determinar la altura máxima alcanzada.
h(94)=−16(94)2+72(94)=−16(8116)+72(94)=−81+162=81
Respuesta:
La altura máxima del proyectil es81 pies.
Encontrar el vértice completando el cuadrado
En esta sección, demostramos un enfoque alternativo para encontrar el vértice. Cualquier función cuadrática sef(x)=ax2+bx+c puede reescribir en forma de vértice 14,
f(x)=a(x−h)2+k
En esta forma, el vértice es(h,k). Para ver que este es el caso, considere graficarf(x)=(x−2)2+3 usando las transformaciones.
y=x2Basicsquaringfunctiony=(x−2)2Horizontalshiftright2unitsy=(x−2)2+3Verticalshiftup3units
Usa estas traducciones para bosquejar la gráfica,
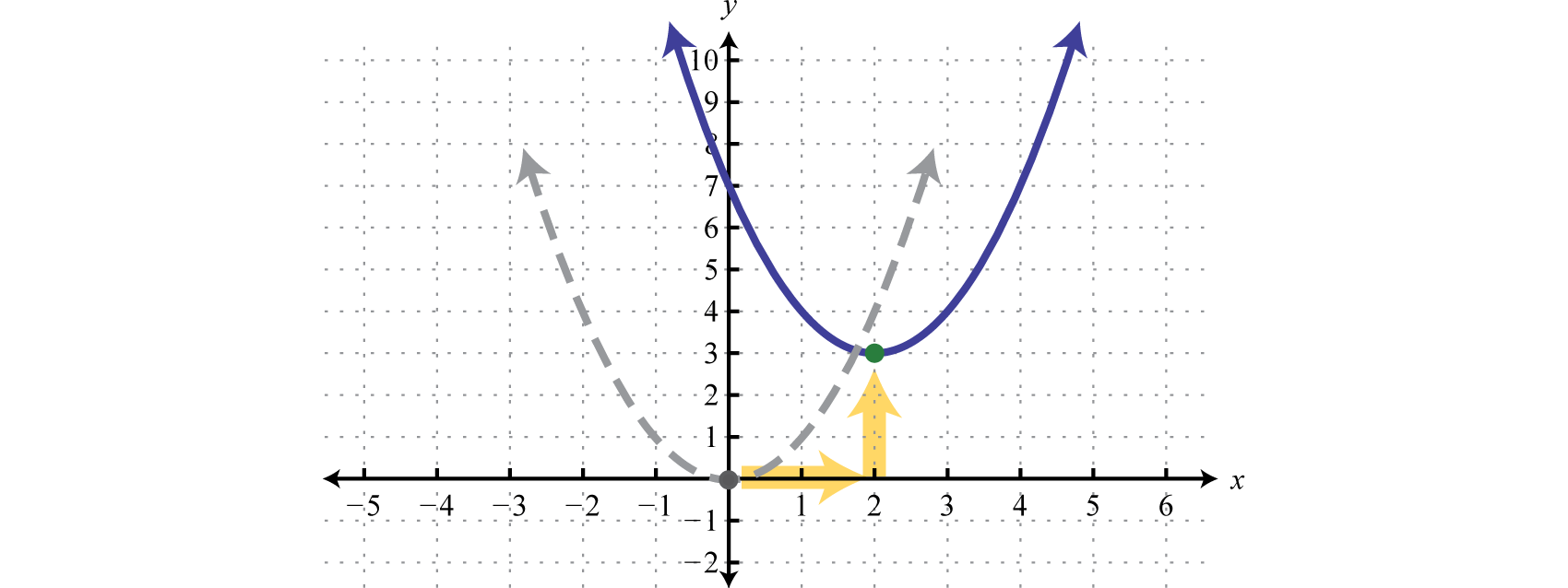
Aquí podemos ver que el vértice es(2,3).
f(x)=a(x−h)2+k↓↓f(x)=(x−2)2+3
Cuando la ecuación está en esta forma, podemos leer el vértice directamente de ella.
Ejemplo6.4.7:
Determinar el vértice:f(x)=2(x+3)2−2.
Solución
Reescriba la ecuación de la siguiente manera antes de determinarh yk.
f(x)=a(x−h)2+k↓↓f(x)=2[x−(−3)]2+(−2)
Aquíh=−3 yk=−2.
Respuesta:
El vértice es(−3,−2).
A menudo la ecuación no se da en forma de vértice. Para obtener este formulario, complete el cuadrado.
Ejemplo6.4.8:
Reescribe en forma de vértice y determina el vértice:f(x)=x2+4x+9.
Solución
Comience por dejar espacio para el término constante que completa la plaza.
f(x)=x2+4x+9=x2+4x+___+9−___
La idea es sumar y restar el valor que completa el cuadrado,(b2)2, y luego factorial. En este caso, sumar y restar(42)2=(2)2=4.
f(x)=x2+4x+9Addandsubtract4.=x2+4x+4+9−4Factor.=(x2+4x+4)+5=(x+3)(x+2)+5=(x+2)2+5
Sumar y restar el mismo valor dentro de una expresión no lo cambia. Hacerlo equivale a sumar0. Una vez que la ecuación está en esta forma, podemos determinar fácilmente el vértice.
f(x)=a(x−h)2+k↓↓f(x)=(x−(−2))2+5
Aquíh=−2 yk=5.
Respuesta:
El vértice es(−2,5).
Si hay un coeficiente principal distinto de1, entonces primero debemos facturar el coeficiente principal a partir de los dos primeros términos del trinomio.
Ejemplo6.4.9:
Reescribe en forma de vértice y determina el vértice:f(x)=2x2−4x+8.
Solución
Ya quea=2, factifique esto de los dos primeros términos para completar el cuadrado. Deja espacio dentro de los paréntesis para sumar y restar el valor que completa el cuadrado.
f(x)=2x2−4x+8=2(x2−2x)+8
Ahora−2 utilízalo para determinar el valor que completa el cuadrado. En este caso,(−22)2=(−1)2=1. Sumar y restar1 y factificar de la siguiente manera:
f(x)=2x2−4x+8=2(x2−2x+___−___)+8Addandsubtract1.=2(x2−2x+1−1)+8Factor.=2[(x−1)(x−1)−1]+8=2[(x−1)2−1]+8Distributethe2.=2(x−1)2−2+8=2(x−1)2+6
De esta forma, podemos determinar fácilmente el vértice.
f(x)=a(x−h)2+k↓↓f(x)=2(x−1)2+6
Aquíh=1 yk=6.
Respuesta:
El vértice es(1,6).
Ejercicio6.4.1
Reescribe en forma de vértice y determina el vértice:f(x)=−2x2−12x+3.
- Contestar
-
f(x)=−2(x+3)2+21; vértice:(−3,21)
www.youtube.com/v/cmwmn6oz2di
Claves para llevar
- La gráfica de cualquier función cuadráticaf(x)=ax2+bx+ca,b, donde, yc son números reales ya≠0, se llama parábola.
- Al graficar una parábola siempre encuentra el vértice y lay -intercepción. Si lasx -intercepciones existen, encontrarlas también. Además, asegúrese de encontrar soluciones de pares ordenados a ambos lados de la línea de simetría,x=−b2a.
- Utilice el coeficiente inicial,a, para determinar si una parábola se abre hacia arriba o hacia abajo. Sia es positivo, entonces se abre hacia arriba. Sia es negativo, entonces se abre hacia abajo.
- El vértice de cualquier parábola tiene unx -valor igual a−b2a. Después de encontrar elx -valor del vértice, sustituirlo por la ecuación original para encontrar ely -valor correspondiente. Estey -valor es un máximo si la parábola se abre hacia abajo, y es un mínimo si la parábola se abre hacia arriba.
- El dominio de una parábola que se abre hacia arriba o hacia abajo consiste en todos los números reales. El rango está limitado por ely -valor del vértice.
- Un enfoque alternativo para encontrar el vértice es reescribir la función cuadrática en la formaf(x)=a(x−h)2+k. Cuando está en esta forma, el vértice es(h,k) y se puede leer directamente de la ecuación. Para obtener esta forma, tomaf(x)=ax2+bx+c y completa la plaza.
Ejercicio6.4.3
¿La parábola se abre hacia arriba o hacia abajo? Explique.
- y=x2−9x+20
- y=x2−12x+32
- y=−2x2+5x+12
- y=−6x2+13x−6
- y=64−x2
- y=−3x+9x2
- Contestar
-
1. Al alza
3. A la baja
5. A la baja
Ejercicio6.4.4
Determinar lasx - yy -intercepciones.
- y=x2+4x−12
- y=x2−13x+12
- y=2x2+5x−3
- y=3x2−4x−4
- y=−5x2−3x+2
- y=−6x2+11x−4
- y=4x2−27
- y=9x2−50
- y=x2−x+1
- y=x2−6x+4
- Contestar
-
1. x-intercepta:(−6,0),(2,0);y -interceptar:(0,−12)
3. x-intercepta:(−3,0),(12,0);y -interceptar:(0,−3)
5. x-intercepta:(−1,0),(25,0);y -interceptar:(0,2)
7. x-intercepta:(−3√32,0),(3√32,0);y -interceptar:(0,−27)
9. x-intercepta: ninguno;y -interceptar:(0,1)
Ejercicio6.4.5
Encuentra el vértice y la línea de simetría.
- y=−x2+10x−34
- y=−x2−6x+1
- y=−4x2+12x−7
- y=−9x2+6x+2
- y=4x2−1
- y=x2−16
- Contestar
-
1. Vértice:(5,−9); línea de simetría:x=5
3. Vértice:(32,2); línea de simetría:x=32
5. Vértice:(0,−1); línea de simetría:x=0
Ejercicio6.4.6
Gráfica. Encuentra el vértice y lay -intercepción. Además, encuentra losx -interceptos si existen.
- f(x)=x2−2x−8
- f(x)=x2−4x−5
- f(x)=−x2+4x+12
- f(x)=−x2−2x+15
- f(x)=x2−10x
- f(x)=x2+8x
- f(x)=x2−9
- f(x)=x2−25
- f(x)=1−x2
- f(x)=4−x2
- f(x)=x2−2x+1
- f(x)=x2+4x+4
- f(x)=−4x2+12x−9
- f(x)=−4x2−4x+3
- f(x)=x2−2
- f(x)=x2−3
- f(x)=−4x2+4x−3
- f(x)=4x2+4x+3
- f(x)=x2−2x−2
- f(x)=x2−6x+6
- f(x)=−2x2+6x−3
- f(x)=−4x2+4x+1
- f(x)=x2+3x+4
- f(x)=−x2+3x−4
- f(x)=−2x2+3
- f(x)=−2x2−1
- f(x)=2x2+4x−3
- f(x)=3x2+2x−2
- Contestar
-
1.
Figura6.4.11 3.
Figura6.4.12 5.
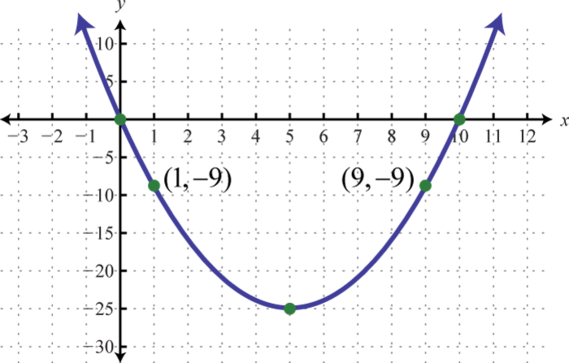
Figura6.4.13 7.
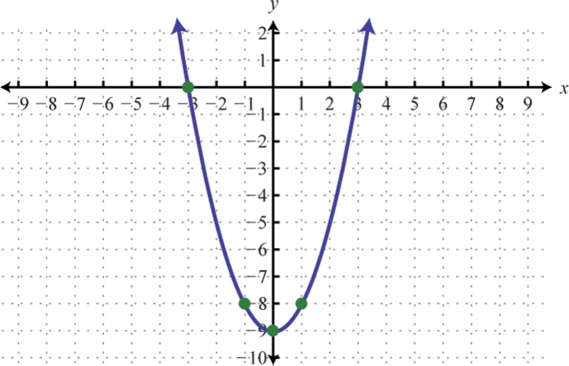
Figura6.4.14 9.
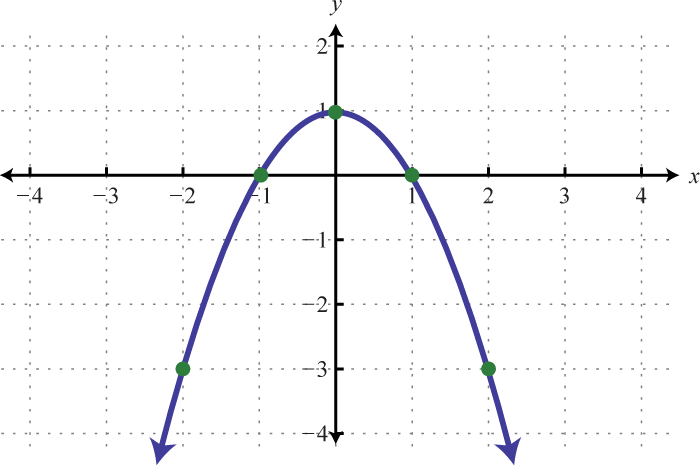
Figura6.4.15 11.
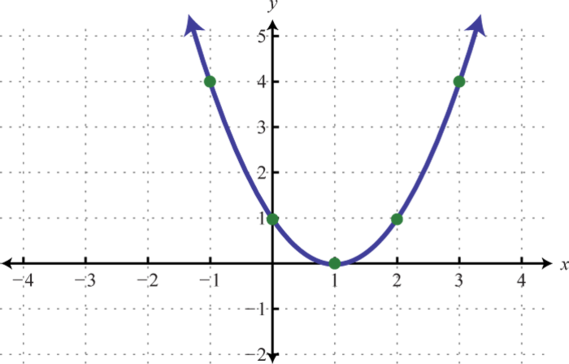
Figura6.4.16 13.
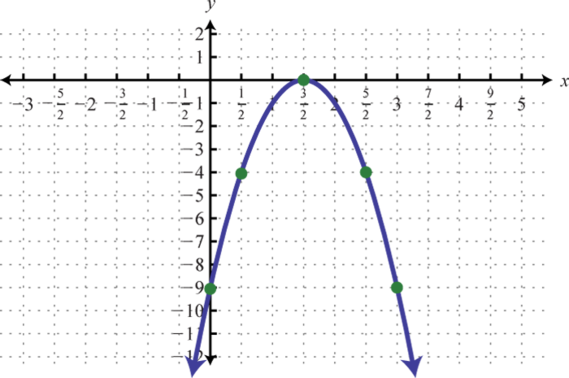
Figura6.4.17 15.
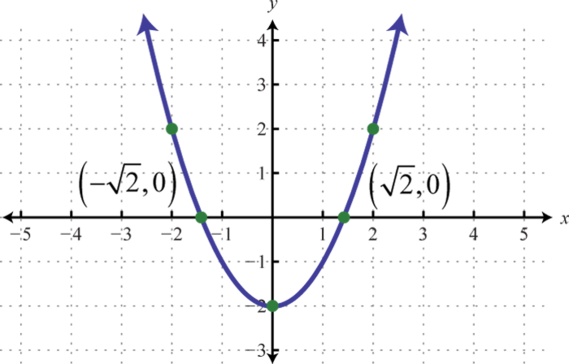
Figura6.4.18 17.
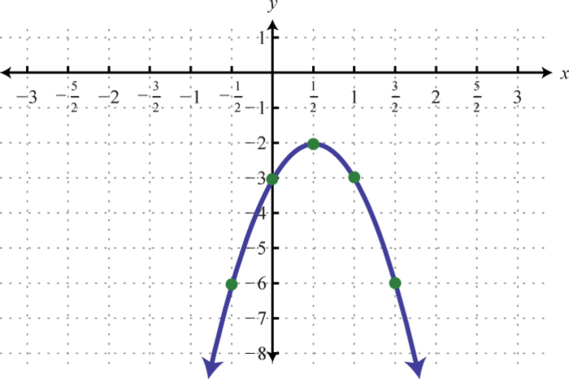
Figura6.4.19 19.
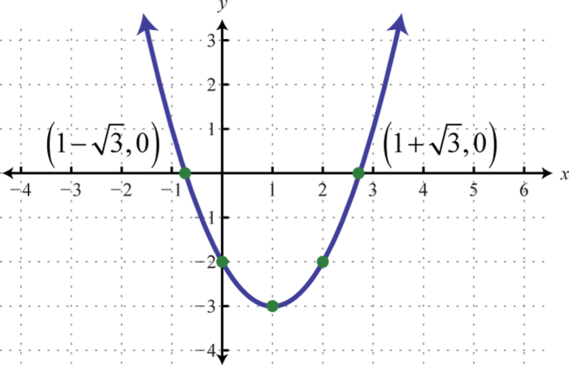
Figura6.4.20 21.
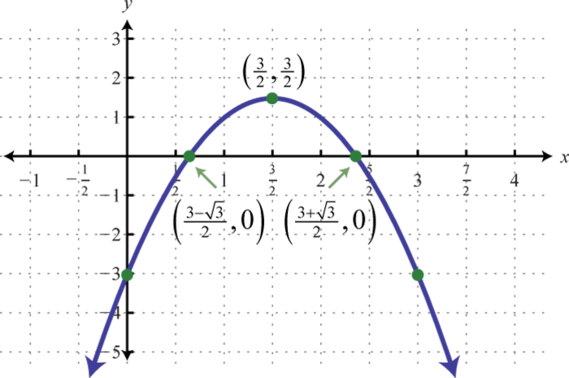
Figura6.4.21 23.
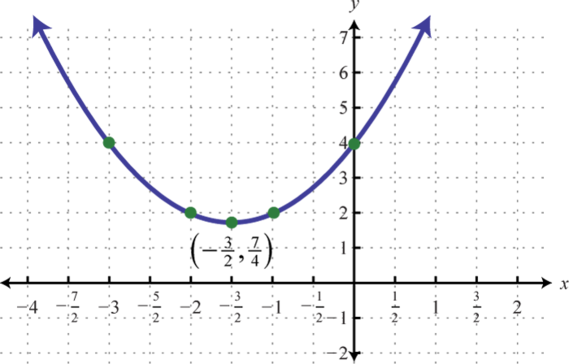
Figura6.4.22 25.
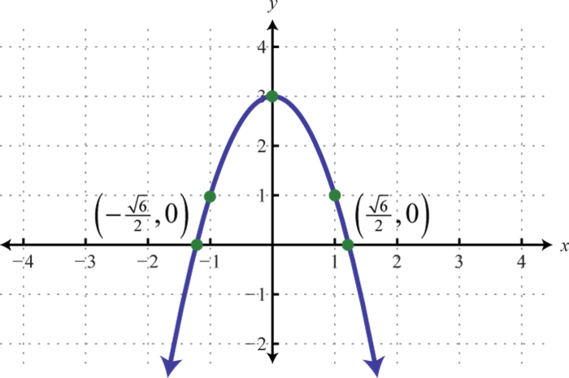
Figura6.4.23 27.
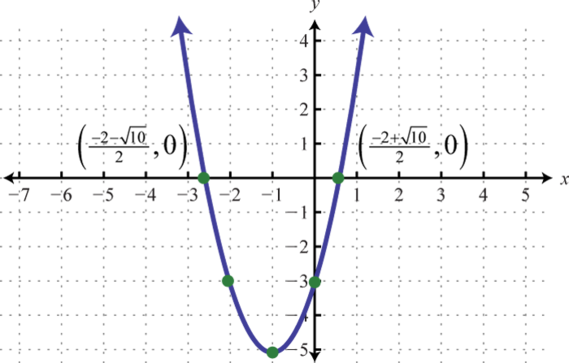
Figura6.4.24
Ejercicio6.4.7
Determinar ely valor máximo o mínimo.
- y=−x2−6x+1
- y=−x2−4x+8
- y=25x2−10x+5
- y=16x2−24x+7
- y=−x2
- y=1−9x2
- y=20x−10x2
- y=12x+4x2
- y=3x2−4x−2
- y=6x2−8x+5
- y=x2−5x+1
- y=1−x−x2
- Contestar
-
1. Máximo:y=10
3. Mínimo:y=45
5. Máximo:y=0
7. Máximo:y=10
9. Mínimo:y=−103
11. Mínimo:y=−214
Ejercicio6.4.8
Dadas las siguientes funciones cuadráticas, determinar el dominio y el rango.
- f(x)=3x2+30x+50
- f(x)=5x2−10x+1
- g(x)=−2x2+4x+1
- g(x)=−7x2−14x−9
- f(x)=x2+x−1
- f(x)=−x2+3x−2
- La altura en pies que alcanza un beisbol arrojado hacia arriba a una velocidad de48 pies por segundo desde el suelo viene dada por la funciónh(t)=−16t2+48t, dondet representa el tiempo en segundos después de que se lanza la pelota. ¿Cuál es la altura máxima del beisbol y cuánto tiempo se tarda en alcanzar esa altura?
- La altura en pies de un proyectil lanzado hacia arriba desde un montículo viene dada por la funciónh(t)=−16t2+96t+4, dondet representa segundos después del lanzamiento. ¿Cuál es la altura máxima?
- El beneficio en dólares generado por la producción y venta de lámparasx personalizadas viene dado por la funciónP(x)=−10x2+800x−12,000. ¿Cuál es el beneficio máximo?
- El beneficio en dólares generado por la producción y venta de un artículo en particular se modela por la fórmulaP(x)=100x−0.0025x2, dondex representa el número de unidades producidas y vendidas. ¿Qué número de unidades se deben producir y vender para maximizar los ingresos?
- El número promedio de aciertos a un sitio Web de una estación de radio está modelado por la fórmulaf(x)=450t2−3,600t+8,000, dondet representa el número de horas desde la8:00 mañana ¿A qué hora del día es mínimo el número de visitas al sitio Web?
- El valor en dólares de un auto nuevo es modelado por la fórmulaV(t)=125t2−3,000t+22,000, dondet representa el número de años desde que fue comprado. Determinar el valor mínimo del automóvil.
- El costo de producción diario en dólares de una empresa de fabricación textil que produce uniformes personalizados se modela por la fórmulaC(x)=0.02x2−20x+10,000, dondex representa el número de uniformes producidos.
- ¿Cuántos uniformes se deben producir para minimizar los costos diarios de producción?
- ¿Cuál es el costo mínimo de producción diario?
- El área en pies cuadrados de cierta pluma rectangular viene dada por la fórmulaA=14w−w2, dondew representa el ancho en pies. Determinar el ancho que produce el área máxima.
- Contestar
-
1. Dominio:(−∞,∞); rango:[−25,∞)
3. Dominio:(−∞,∞); rango:(−∞,3]
5. Dominio:(−∞,∞); rango:[−54,∞)
7. La altura máxima de36 los pies ocurre después de1.5 segundos.
9. $4,000
11. 12:00p.m.
13. (1)500 uniformes (2) $5,000
Ejercicio6.4.9
Determinar el vértice.
- y=−(x−5)2+3
- y=−2(x−1)2+7
- y=5(x+1)2+6
- y=3(x+4)2+10
- y=−5(x+8)2−1
- y=(x+2)2−5
- Contestar
-
1. (5,3)
3. (−1,6)
5. (−8,−1)
Ejercicio6.4.10
Reescribe en forma de vérticey=a(x−h)2+k y determina el vértice.
- y=x2−14x+24
- y=x2−12x+40
- y=x2+4x−12
- y=x2+6x−1
- y=2x2−12x−3
- y=3x2−6x+5
- y=−x2+16x+17
- y=−x2+10x
- Contestar
-
1. y=(x−7)2−25; vértice:(7,−25)
3. y=(x+2)2−16; vértice:(−2,−16)
5. y=2(x−3)2−21; vértice:(3,−21)
7. y=−(x−8)2+81; vértice:(8,81)
Ejercicio6.4.11
Gráfica. Encuentra el vértice y lay -intercepción. Además, encuentra losx -interceptos si existen.
- f(x)=x2−1
- f(x)=x2+1
- f(x)=(x−1)2
- f(x)=(x+1)2
- f(x)=(x−4)2−9
- f(x)=(x−1)2−4
- f(x)=−2(x+1)2+8
- f(x)=−3(x+2)2+12
- f(x)=−5(x−1)2
- f(x)=−(x+2)2
- f(x)=−4(x−1)2−2
- f(x)=9(x+1)2+2
- f(x)=(x+5)2−15
- f(x)=2(x−5)2−3
- f(x)=−2(x−4)2+22
- f(x)=2(x+3)2−13
- Contestar
-
1.
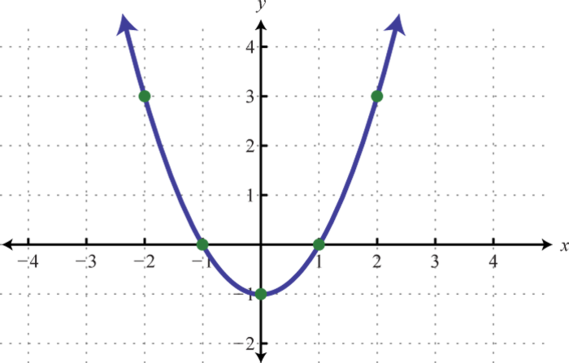
Figura6.4.25 3.
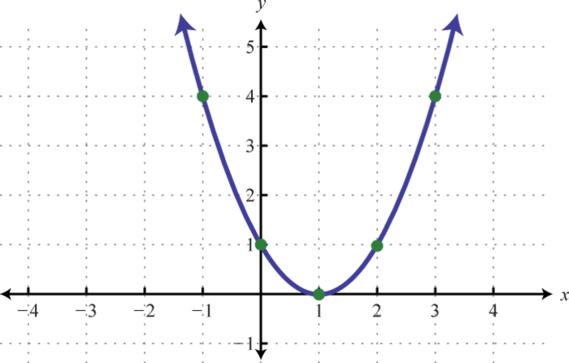
Figura6.4.26 5.
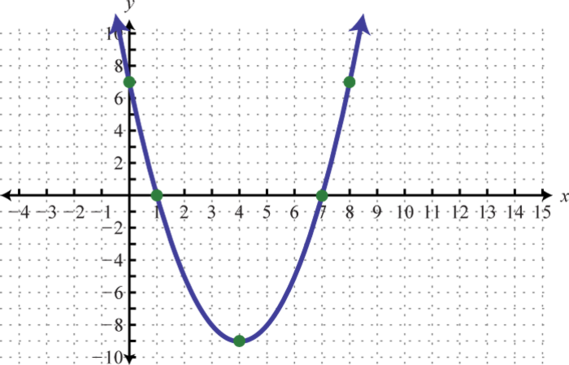
Figura6.4.27 7.
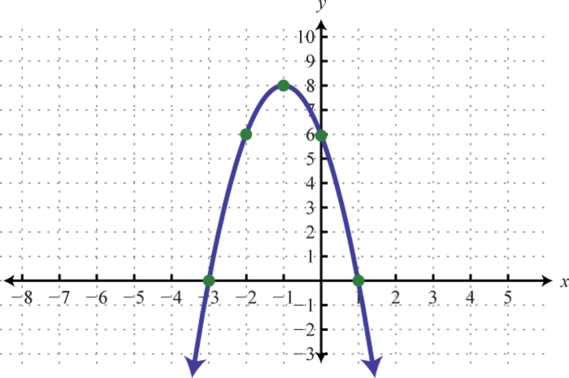
Figura6.4.28 9.
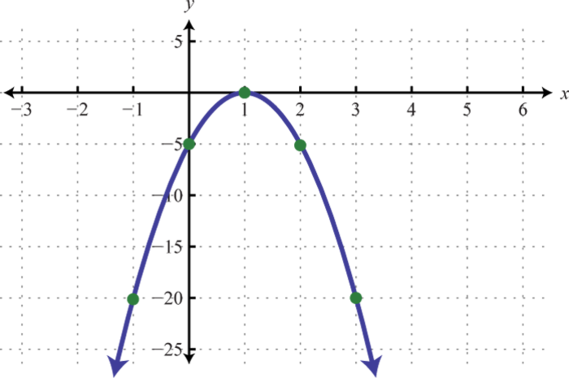
Figura6.4.29 11.
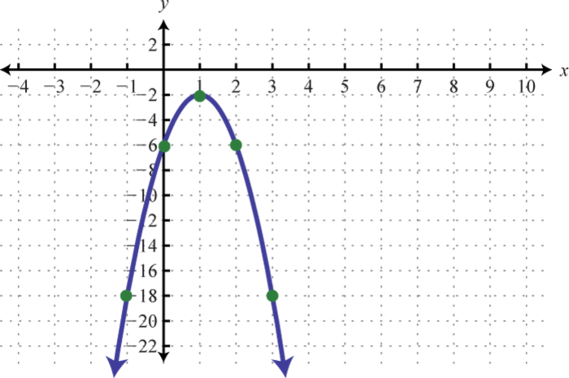
Figura6.4.30 13.
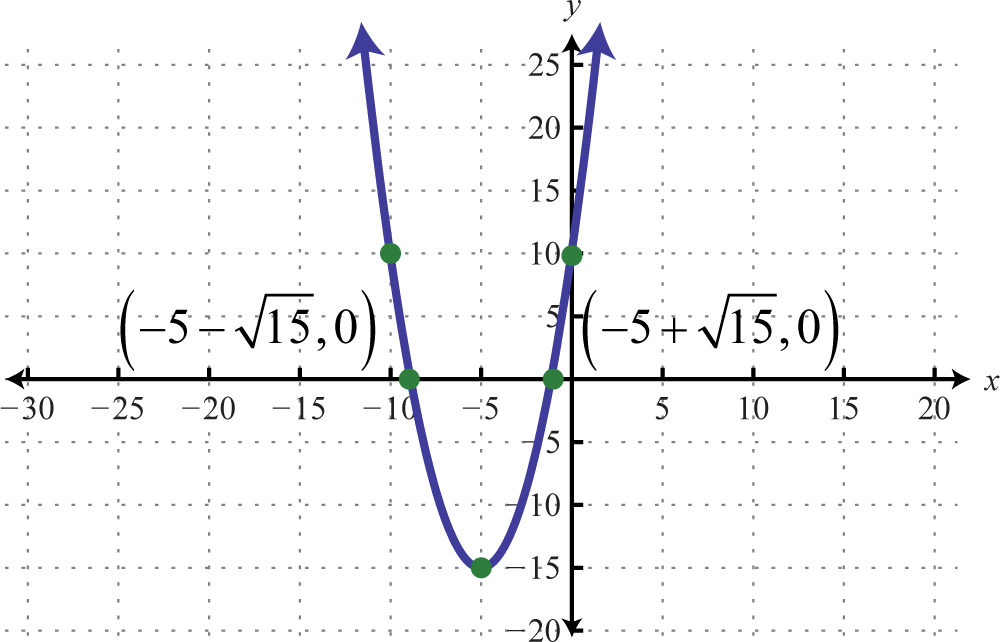
Figura6.4.31 15.
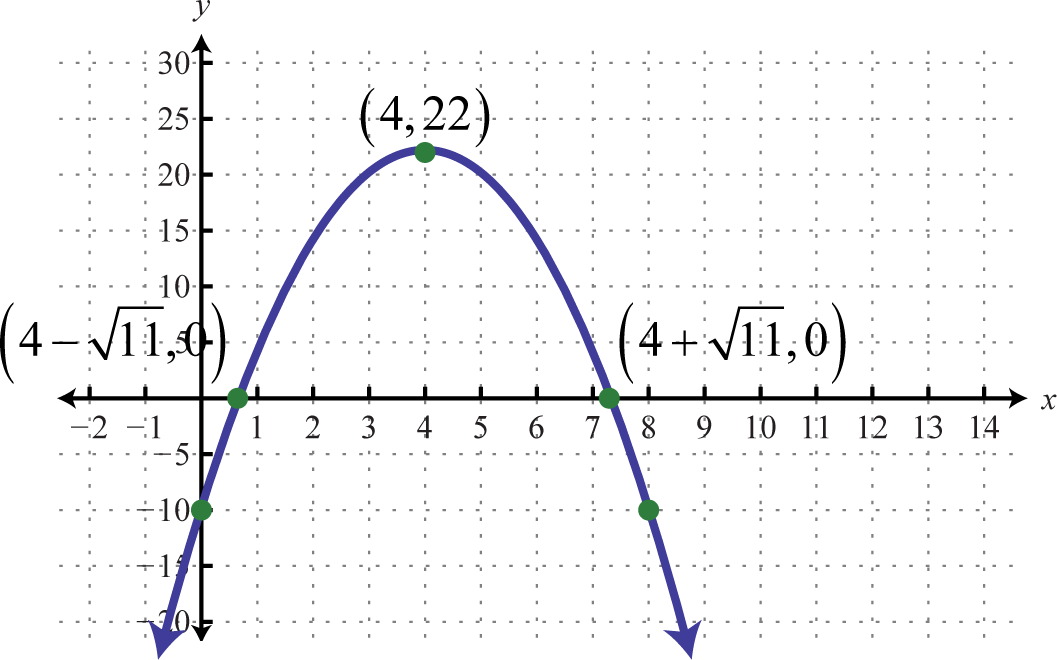
Figura6.4.32
Ejercicio6.4.12
- Anota tu plan para graficar una parábola en un examen. ¿Qué buscarás y cómo presentarás tu respuesta? Comparte tu plan en el panel de discusión.
- ¿Por qué cualquier parábola que se abre hacia arriba o hacia abajo es una función? Explique a un compañero de clase cómo determinar el dominio y el rango.
- Investigue y discuta formas de encontrar una función cuadrática que tenga una gráfica que pase por tres puntos dados cualquiera. Comparte una lista de pasos así como un ejemplo de cómo hacerlo.
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar
Notas al pie
10 La gráfica en forma de U de cualquier función cuadrática definida porf(x)=ax2+bx+c, dóndea,b, yc son números reales ya≠0.
11 El punto que define el mínimo o máximo de una parábola.
12 La línea vertical a través del vértice,x=−b2a, alrededor de la cual la parábola es simétrica.
13 Término utilizado al hacer referencia a la línea de simetría.
14 Una función cuadrática escrita en la formaf(x)=a(x−h)2+k.


