4.1E: Funciones Lineales (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 111859

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1. Determinar si la ecuación algebraica es lineal. $2 x+3 y=7$
2. Determinar si la ecuación algebraica es lineal. $6 x^{2}-y=5$
3. Determinar si la función está aumentando o disminuyendo. \[f(x)=7 x-2 \nonumber\]
4. Determinar si la función está aumentando o disminuyendo. \[g(x)=-x+2 \nonumber\]
5. Dado cada conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones dadas, si es posible.
Pasa a través de (7,5) y (3,17)
6. Dado cada conjunto de información, encontrar una ecuación lineal que satisfaga las condiciones dadas, si es posible.
$x$-interceptar en (6,0) y$y$ -interceptar en (0,10)
7. Encuentra la pendiente de la línea que se muestra en la gráfica.

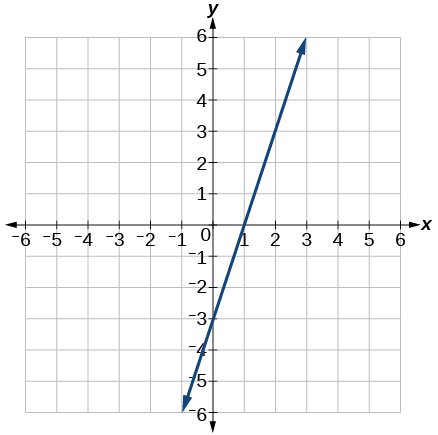
$Esta es una gráfica de una línea creciente con una intercepción y de -3 e intercepción x de 1 en un plano de coordenadas x, y. Los ejes x e y varían de -6 a 6.$

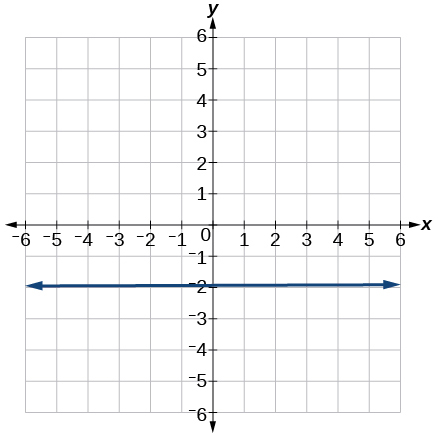
$Esta es una gráfica de una línea con una intercepción y de -2 y sin intercepciones x en un plano de coordenadas x, y. El rango de los ejes x e y de -6 a 6$

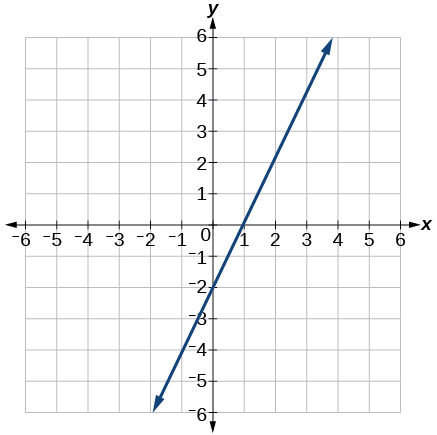
$Esta es una gráfica de una línea con una intercepción y de -2 e intercepción x de 1 en un plano de coordenadas x, y. Los ejes x e y varían de -6 a 6.$

¿La siguiente tabla representa una función lineal? Si es así, encuentra la ecuación lineal que modela los datos.

x	—4	0	2	10
*g (x)*	18	—2	—12	—52

¿La siguiente tabla representa una función lineal? Si es así, encuentra la ecuación lineal que modela los datos.

x	6	8	12	26
*g (x)*	—8	—12	—18	—46

12. En junio$1^{\text {st }}$, una empresa tiene$\$ 4,000,000$ ganancias. Si entonces la empresa pierde 150.000 dólares diarios a partir de entonces en el mes de junio, ¿cuál es la ganancia$n^{\text {th }}$ de la compañía después de junio$1^{\text {st }}$?

Para los siguientes ejercicios, determine si las líneas dadas por las ecuaciones siguientes son paralelas, perpendiculares, o no paralelas ni perpendiculares:

13. \[\begin{align*} 2 x-6 y &=12 \\[4pt] -x+3 y &=1 \end{align*}\]

14\[\begin{align*} y &=\frac{1}{3} x-2 \\[4pt] 3 x+y &=-9 \end{align*}\]

Para los siguientes ejercicios, encuentre las intercepciones$x$$y$ - y - de la ecuación dada

15. $7 x+9 y=-63$
16. $f(x)=2 x-1$

Para los siguientes ejercicios, utilice las descripciones de los pares de líneas para encontrar las pendientes de la Línea 1 y la Línea$2 .$ ¿Cada par de líneas es paralela, perpendicular o ninguna?

17.

Línea 1: Pasa a través (5,11) y (10,1)
Línea 2: Pasa a través de (-1,3) y (-5,11)

18.

Línea 1: Pasa a través de (8, -10) y (0, -26)
Línea 2: Pasa a través de (2,5) y (4,4)

19. Escribe una ecuación para una línea perpendicular al punto$f(x)=5 x-1$ y que pasa por él (5,20).

20. Encuentra la ecuación de una línea con una$y$ - intercepción de (0,2) y pendiente$-\frac{1}{2}$.

23. Una empresa de alquiler de autos ofrece dos planes para rentar un auto.

Plan A: 25 dólares por día y 10 centavos por milla
Plan B: 50 dólares por día con kilometraje ilimitado gratuito

¿Cuántas millas necesitarías conducir para el plan B para ahorrarte dinero?