7.4: Sistemas de Ecuaciones No Lineales y Desigualdades - Dos Variables
- Page ID
- 117032
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Resolver un sistema de ecuaciones no lineales mediante sustitución.
- Resolver un sistema de ecuaciones no lineales usando eliminación.
- Graficar una desigualdad no lineal.
- Graficar un sistema de desigualdades no lineales.
El cometa Halley (Figura\(\PageIndex{1}\)) orbita el sol aproximadamente una vez cada\(75\) año. Su trayectoria puede considerarse como una elipse muy alargada. Otros cometas siguen caminos similares en el espacio. Estas trayectorias orbitales pueden ser estudiadas utilizando sistemas de ecuaciones. Estos sistemas, sin embargo, son diferentes a los que consideramos en la sección anterior debido a que las ecuaciones no son lineales.

Figura\(\PageIndex{1}\): Halley's Comet (crédito: “NASA Blueshift” /Flickr)
En esta sección, consideraremos la intersección de una parábola y una línea, un círculo y una línea, y un círculo y una elipse. Los métodos para resolver sistemas de ecuaciones no lineales son similares a los de las ecuaciones lineales.
Resolver un Sistema de Ecuaciones No Lineales Usando Sustitución
Un sistema de ecuaciones no lineales es un sistema de dos o más ecuaciones en dos o más variables que contienen al menos una ecuación que no es lineal. Recordemos que una ecuación lineal puede tomar la forma\(Ax+By+C=0\). Cualquier ecuación que no se pueda escribir de esta forma en no lineal. El método de sustitución que utilizamos para sistemas lineales es el mismo método que usaremos para sistemas no lineales. Resolvemos una ecuación para una variable y luego sustituimos el resultado por la segunda ecuación para resolver por otra variable, y así sucesivamente. Sin embargo, existe una variación en los posibles resultados.
Intersección de una parábola y una línea
Existen tres posibles tipos de soluciones para un sistema de ecuaciones no lineales que involucran una parábola y una línea.
La figura\(\PageIndex{2}\) ilustra posibles conjuntos de soluciones para un sistema de ecuaciones que involucran una parábola y una línea.
- Sin solución - La línea nunca cruzará la parábola.
- Una solución - La línea es tangente a la parábola e interseca la parábola exactamente en un punto.
- Dos soluciones - La línea cruza en el interior de la parábola e interseca la parábola en dos puntos.
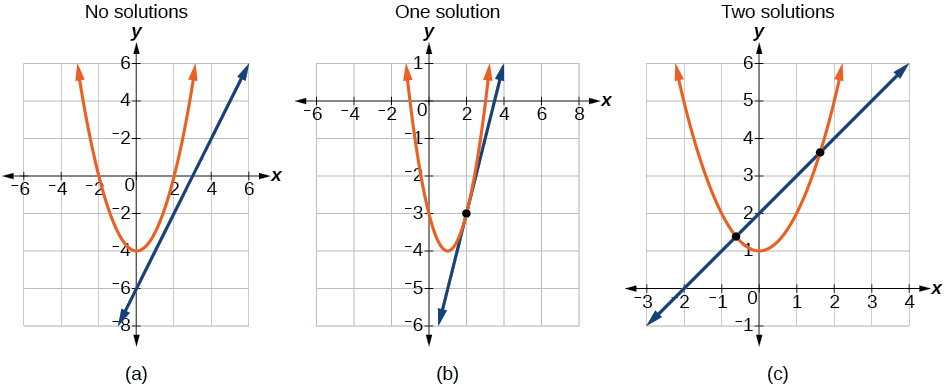
Figura\(\PageIndex{2}\)
- Resolver la ecuación lineal para una de las variables.
- Sustituir la expresión obtenida en el paso uno en la ecuación de parábola.
- Resolver para la variable restante.
- Consulta tus soluciones en ambas ecuaciones.
Resolver el sistema de ecuaciones.
\[\begin{align*} x−y &= −1\nonumber \\ y &= x^2+1 \nonumber \end{align*}\]
Solución
Resuelva la primera ecuación para\(x\) y luego sustituya la expresión resultante en la segunda ecuación.
\[\begin{align*} x−y &=−1\nonumber \\ x &= y−1 \;\; & \text{Solve for }x.\nonumber \\\nonumber \\ y &=x^2+1\nonumber \\ y & ={(y−1)}^2+1 \;\; & \text{Substitute expression for }x. \nonumber \end{align*}\]
Expande la ecuación y ponla igual a cero.
\[ \begin{align*} y & ={(y−1)}^2+1\nonumber \\ &=(y^2−2y+1)+1\nonumber \\ &=y^2−2y+2\nonumber \\ 0 &= y^2−3y+2\nonumber \\ &= (y−2)(y−1) \nonumber \end{align*}\]
Resolviendo para\(y\) da\(y=2\) y\(y=1\). A continuación, sustituya cada valor por\(y\) en la primera ecuación para resolver\(x\). Siempre sustituya el valor en la ecuación lineal para verificar si hay soluciones extrañas.
\[\begin{align*} x−y &=−1\nonumber \\ x−(2) &= −1\nonumber \\ x &= 1\nonumber \\ x−(1) &=−1\nonumber \\ x &= 0 \nonumber \end{align*}\]
Las soluciones son\((1,2)\) y\((0,1)\), que pueden verificarse sustituyendo estos\((x,y)\) valores en ambas ecuaciones originales (Figura\(\PageIndex{3}\)).
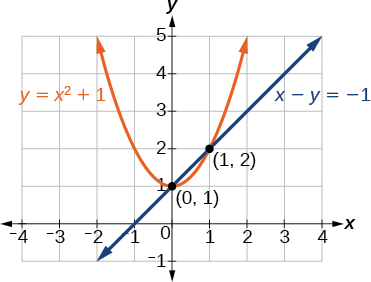
Figura\(\PageIndex{3}\)
Sí, pero porque\(x\) está cuadrado en la segunda ecuación esto podría darnos soluciones extrañas para\(x\).
Para\(y=1\)
\[\begin{align*} y &= x^2+1\nonumber \\ y &= x^2+1\nonumber \\ x^2 &= 0\nonumber \\ x &= \pm \sqrt{0}=0 \nonumber \end{align*}\]
Esto nos da el mismo valor que en la solución.
Para\(y=2\)
\[\begin{align*} y &= x^2+1\nonumber \\ 2 &= x^2+1\nonumber \\ x^2 &= 1\nonumber \\ x &= \pm \sqrt{1}=\pm 1 \nonumber \end{align*}\]
Observe que\(−1\) es una solución ajena.
Resolver el sistema de ecuaciones dado por sustitución.
\[\begin{align*} 3x−y &= −2\nonumber \\ 2x^2−y &= 0 \nonumber \end{align*}\]
- Contestar
-
\(\left(−\dfrac{1}{2},\dfrac{1}{2}\right)\)y\((2,8)\)
Intersección de un círculo y una línea
Al igual que con una parábola y una línea, hay tres posibles resultados a la hora de resolver un sistema de ecuaciones que representan un círculo y una línea.
La figura\(\PageIndex{4}\) ilustra posibles conjuntos de soluciones para un sistema de ecuaciones que involucran un círculo y una línea.
- Sin solución - La línea no interseca el círculo.
- Una solución - La línea es tangente al círculo e interseca el círculo exactamente en un punto.
- Dos soluciones - La línea cruza el círculo y lo cruza en dos puntos.

Figura\(\PageIndex{4}\)
- Resolver la ecuación lineal para una de las variables.
- Sustituir la expresión obtenida en el paso uno en la ecuación por el círculo.
- Resolver para la variable restante.
- Consulta tus soluciones en ambas ecuaciones.
Encuentra la intersección del círculo dado y la línea dada por sustitución.
\[\begin{align*} x^2+y^2 &= 5\nonumber \\ y &= 3x−5 \nonumber \end{align*}\]
Solución
Una de las ecuaciones ya fue resuelta para\(y\). Vamos a sustituir\(y=3x−5\) en la ecuación el círculo.
\[\begin{align*} x^2+{(3x−5)}^2 &= 5\nonumber \\ x^2+9x^2−30x+25 &= 5\nonumber \\ 10x^2−30x+20 &= 0 \end{align*} \]
Ahora, facetamos y resolvemos para\(x\).
\[\begin{align*} 10(x2−3x+2) &= 0\nonumber \\ 10(x−2)(x−1) &= 0\nonumber \\ x &= 2\nonumber \\ x &= 1 \nonumber \end{align*}\]
Sustituya los dos\(x\) valores en la ecuación lineal original para resolver\(y\).
\[\begin{align*} y &= 3(2)−5\nonumber \\ &= 1\nonumber \\ y &= 3(1)−5\nonumber \\ &= −2 \nonumber \end{align*}\]
La línea cruza el círculo en\((2,1)\) y\((1,−2)\), que puede verificarse sustituyendo estos\((x,y)\) valores en ambas ecuaciones originales (Figura\(\PageIndex{5}\)).
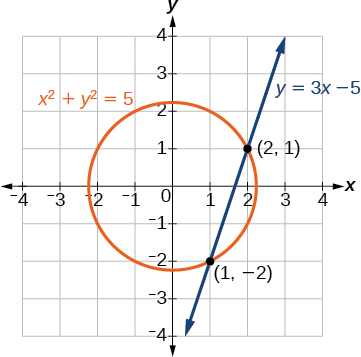
Figura\(\PageIndex{5}\)
Resolver el sistema de ecuaciones no lineales.
\[\begin{align*} x^2+y^2 &= 10\nonumber \\ x−3y &= −10 \nonumber \end{align*}\]
- Contestar
-
\((−1,3)\)
Resolver un Sistema de Ecuaciones No Lineales Usando Eliminación
Hemos visto que la sustitución suele ser el método preferido cuando un sistema de ecuaciones incluye una ecuación lineal y una ecuación no lineal. Sin embargo, cuando ambas ecuaciones en el sistema tienen variables similares de segundo grado, resolverlas usando eliminación por adición suele ser más fácil que la sustitución. Generalmente, la eliminación es un método mucho más simple cuando el sistema involucra solo dos ecuaciones en dos variables (un sistema de dos por dos), en lugar de un sistema de tres por tres, ya que hay menos pasos. Como ejemplo, investigaremos los posibles tipos de soluciones a la hora de resolver un sistema de ecuaciones que representan un círculo y una elipse.
La figura\(\PageIndex{6}\) ilustra posibles conjuntos de soluciones para un sistema de ecuaciones que involucran un círculo y una elipse.
- Sin solución - El círculo y la elipse no se cruzan. Una forma está dentro de la otra o el círculo y la elipse están a una distancia de la otra.
- Una solución - El círculo y la elipse son tangentes entre sí, y se cruzan exactamente en un punto.
- Dos soluciones - El círculo y la elipse se cruzan en dos puntos.
- Tres soluciones - El círculo y la elipse se cruzan en tres puntos.
- Cuatro soluciones - El círculo y la elipse se cruzan en cuatro puntos.
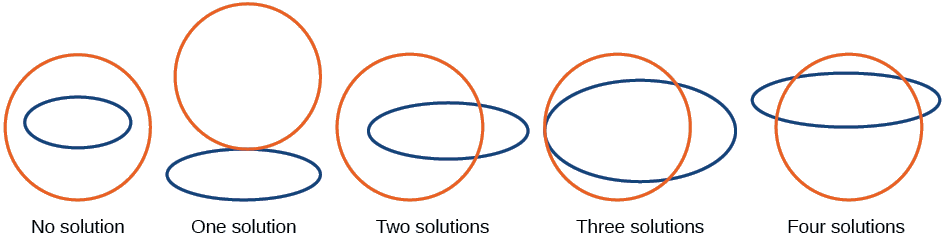
Figura\(\PageIndex{6}\)
Resolver el sistema de ecuaciones no lineales.
\[\begin{align*} x^2+y^2 &= 26 &(1)\nonumber \\ 3x^2+25y^2 &= 100 & (2) \nonumber \end{align*}\]
Solución
Comencemos multiplicando la ecuación (1) por\(−3\), y sumarla a la ecuación (2).
\[\begin{align*} (−3)(x^2+y^2) = (−3)(26)&\nonumber \\ −3x^2−3y^2 = −78 &\nonumber \\ \underline{3x^2+25y^2=100}&\nonumber \\ 22y^2=22& \nonumber \end{align*}\]
Después de sumar las dos ecuaciones juntas, resolvemos para\(y\).
\[\begin{align*} y^2 &= 1\nonumber \\ y &= \pm \sqrt{1}=\pm 1 \nonumber \end{align*}\]
Sustituir\(y=\pm 1\) en una de las ecuaciones y resolver para\(x\).
\[\begin{align*} x^2+{(1)}^2 &= 26\nonumber \\ x^2+1 &= 26\nonumber \\ x^2 &= 25\nonumber \\ x &= \pm \sqrt{25}=\pm 5\nonumber \\ x^2+{(−1)}^2 &= 26\nonumber \\ x^2+1 &= 26\nonumber \\ x^2 &= \pm \sqrt{25}=\pm 5 \nonumber \end{align*}\]
Hay cuatro soluciones:\((5,1)\),\((−5,1)\)\((5,−1)\), y\((−5,−1)\). Ver Figura\(\PageIndex{7}\).
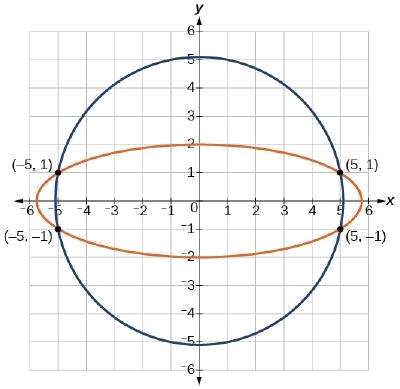
Figura\(\PageIndex{7}\)
Encuentre el conjunto de soluciones para el sistema dado de ecuaciones no lineales.
\[\begin{align*} 4x^2+y^2 &= 13\nonumber \\ x^2+y^2 &= 10 \nonumber \end{align*}\]
- Contestar
-
\({(1,3),(1,−3),(−1,3),(−1,−3)}\)
Graficando una desigualdad no lineal
Todas las ecuaciones en los sistemas que hemos encontrado hasta ahora han implicado igualdades, pero también podemos encontrarnos con sistemas que involucran desigualdades. Ya hemos aprendido a graficar las desigualdades lineales graficando la ecuación correspondiente, y luego sombreando la región representada por el símbolo de desigualdad. Ahora, seguiremos pasos similares para graficar una desigualdad no lineal para que podamos aprender a resolver sistemas de desigualdades no lineales. Una desigualdad no lineal es una desigualdad que contiene una expresión no lineal. Graficar una desigualdad no lineal es muy parecido a graficar una desigualdad lineal.
Recordemos que cuando la desigualdad es mayor que\(y>a\), o menor que\(y<a\), la gráfica se dibuja con una línea discontinua. Cuando la desigualdad es mayor o igual a\(y≥a\), o menor o igual a\(y≤a\), la gráfica se dibuja con una línea sólida. Los gráficos crearán regiones en el plano, y probaremos cada región para una solución. Si un punto de la región funciona, toda la región funciona. Esa es la región que sombreamos (Figura\(\PageIndex{8}\)).
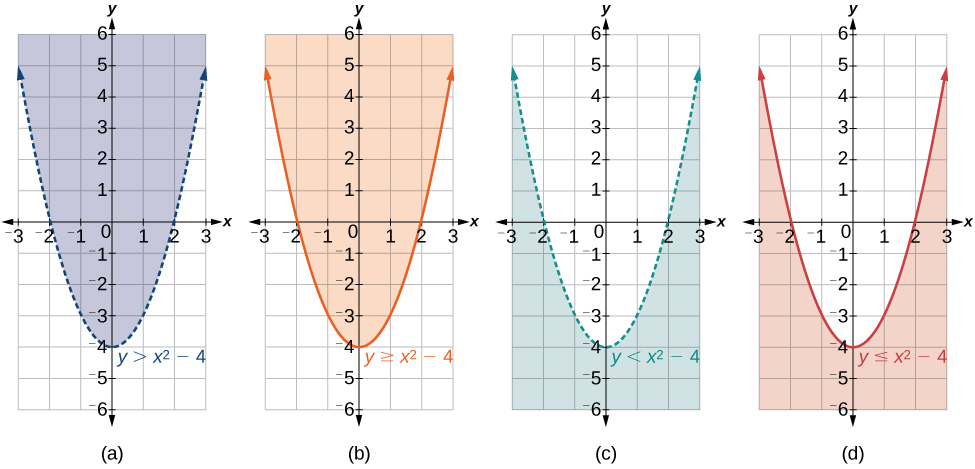
Figura\(\PageIndex{8}\): (a) un ejemplo de\(y>a\); (b) un ejemplo de\(y≥a\); (c) un ejemplo de\(y<a\); (d) un ejemplo de\(y≤a\)
- Grafica la parábola como si se tratara de una ecuación. Este es el límite para la región que es el conjunto de soluciones.
- Si el límite está incluido en la región (el operador es\(≤\) o\(≥\)), la parábola se grafica como una línea continua.
- Si el límite no está incluido en la región (el operador es\(<\) o\(>\)), la parábola se grafica como una línea discontinua.
- Pruebe un punto en una de las regiones para determinar si satisface la declaración de desigualdad. Si la declaración es verdadera, el conjunto de soluciones es la región que incluye el punto. Si la sentencia es falsa, el conjunto de soluciones es la región del otro lado de la línea límite.
- Sombra la región que representa el conjunto de soluciones.
Grafica la desigualdad\(y>x^2+1\).
Solución
Primero, grafica la ecuación correspondiente\(y=x^2+1\). Ya que\(y>x^2+1\) tiene un símbolo mayor que, dibujamos la gráfica con una línea discontinua. Después elegimos puntos para probar tanto dentro como fuera de la parábola. Probemos los puntos
\((0,2)\)y\((2,0)\). Un punto está claramente dentro de la parábola y el otro punto está claramente afuera.
\[\begin{align*} y &> x^2+1\nonumber \\ 2 &> (0)^2+1\nonumber \\ 2 &>1 & \text{True}\nonumber \\\nonumber \\\nonumber \\ 0 &> (2)^2+1\nonumber \\ 0 &> 5 & \text{False} \nonumber \end{align*}\]
La gráfica se muestra en la Figura\(\PageIndex{9}\). Podemos ver que el conjunto de soluciones consiste en todos los puntos dentro de la parábola, pero no en la propia gráfica.
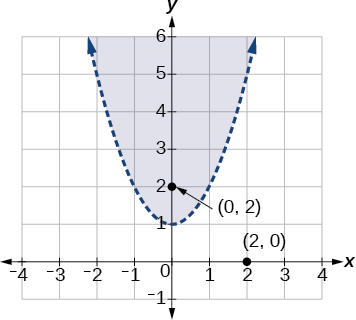
Figura\(\PageIndex{9}\)
Graficando un Sistema de Desigualdades No Lineales
Ahora que hemos aprendido a graficar desigualdades no lineales, podemos aprender a graficar sistemas de desigualdades no lineales. Un sistema de desigualdades no lineales es un sistema de dos o más desigualdades en dos o más variables que contienen al menos una desigualdad que no es lineal. Graficar un sistema de desigualdades no lineales es similar a graficar un sistema de desigualdades lineales. La diferencia es que nuestra gráfica puede resultar en regiones más sombreadas que representan una solución de lo que encontramos en un sistema de desigualdades lineales. La solución a un sistema no lineal de desigualdades es la región de la gráfica donde se superponen las regiones sombreadas de la gráfica de cada desigualdad, o donde las regiones se cruzan, llamada región factible.
- Encuentra los puntos de intersección resolviendo el sistema correspondiente de ecuaciones no lineales.
- Grafica las ecuaciones no lineales.
- Encuentra las regiones sombreadas de cada desigualdad.
- Identificar la región factible como la intersección de las regiones sombreadas de cada desigualdad o el conjunto de puntos comunes a cada desigualdad.
Graficar el sistema dado de desigualdades.
\[\begin{align*} x^2−y &≤ 0\nonumber \\ 2x^2+y &≤ 12 \nonumber \end{align*}\]
Solución
Estas dos ecuaciones son claramente paráolas. Podemos encontrar los puntos de intersección por el proceso de eliminación: Sumar ambas ecuaciones y la variable\(y\) será eliminada. Entonces resolvemos para\(x\).
\[\begin{align*} x^2−y = 0&\nonumber \\ \underline{2x^2+y=12}&\nonumber \\ 3x^2=12&\nonumber \\ x^2=4 &\nonumber \\ x=\pm 2 & \nonumber \end{align*}\]
Sustituir los\(x\) -valores en una de las ecuaciones y resolver para\(y\).
\[\begin{align*} x^2−y &= 0\nonumber \\ {(2)}^2−y &= 0\nonumber \\ 4−y &= 0\nonumber \\ y &= 4\nonumber \\\nonumber \\ {(−2)}^2−y &= 0\nonumber \\ 4−y &= 0\nonumber \\ y &= 4 \nonumber \end{align*}\]
Los dos puntos de intersección son\((2,4)\) y\((−2,4)\). Observe que las ecuaciones se pueden reescribir de la siguiente manera.
\[\begin{align*} x^2-y & ≤ 0\nonumber \\ x^2 &≤ y\nonumber \\ y &≥ x^2\nonumber \\\nonumber \\\nonumber \\ 2x^2+y &≤ 12\nonumber \\ y &≤ −2x^2+12 \nonumber \end{align*}\]
Grafica cada desigualdad. Ver Figura\(\PageIndex{10}\). La región factible es la región entre las dos ecuaciones delimitadas por\(2x^2+y≤12\) en la parte superior e\(x^2−y≤0\) inferior.
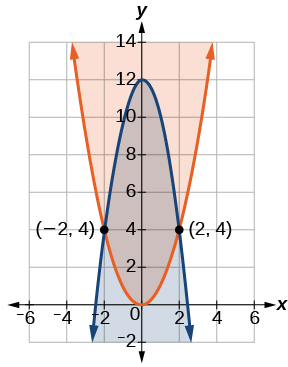
Figura\(\PageIndex{10}\)
Graficar el sistema dado de desigualdades.
\[\begin{align*} y &≥ x^2−1\nonumber \\ x−y &≥ −1 \nonumber \end{align*}\]
- Contestar
-
Sombra el área delimitada por las dos curvas, por encima de la cuadrática y por debajo de la línea.
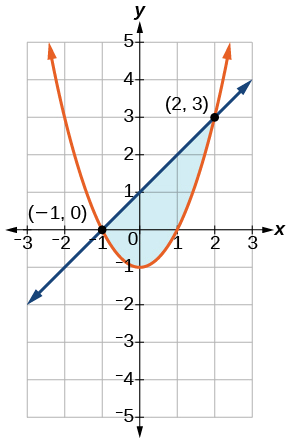
Figura\(\PageIndex{11}\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con ecuaciones no lineales.
Conceptos clave
- Hay tres posibles tipos de soluciones a un sistema de ecuaciones que representan una línea y una parábola: (1) ninguna solución, la línea no cruza la parábola; (2) una solución, la línea es tangente a la parábola; y (3) dos soluciones, la línea cruza la parábola en dos puntos. Ver Ejemplo\(\PageIndex{1}\).
- Hay tres posibles tipos de soluciones a un sistema de ecuaciones que representan un círculo y una línea: (1) ninguna solución, la línea no cruza el círculo; (2) una solución, la línea es tangente a la parábola; (3) dos soluciones, la línea cruza el círculo en dos puntos. Ver Ejemplo\(\PageIndex{2}\).
- Existen cinco posibles tipos de soluciones al sistema de ecuaciones no lineales que representan una elipse y un círculo:
(1) ninguna solución, el círculo y la elipse no se cruzan; (2) una solución, el círculo y la elipse son tangentes entre sí; (3) dos soluciones, el círculo y la elipse se cruzan en dos puntos; (4) tres soluciones, el círculo y la elipse se cruzan en tres lugares; (5) cuatro soluciones, el círculo y la elipse se cruzan en cuatro puntos. Ver Ejemplo\(\PageIndex{3}\). - Una desigualdad se grafica de la misma manera que una ecuación, excepto > o <, dibujamos una línea discontinua y sombreamos la región que contiene el conjunto de soluciones. Ver Ejemplo\(\PageIndex{4}\).
- Las desigualdades se resuelven de la misma manera que las igualdades, pero las soluciones a los sistemas de desigualdades deben satisfacer ambas desigualdades. Ver Ejemplo\(\PageIndex{5}\).


